Методические указания. +Му к практ.работам всс. Методические указания к практическим работам по дисциплине Вычислительные системы и сети Специальность 5В070200 Автоматизация и управление

• Название: Методические указания к практическим работам по дисциплине Вычислительные системы и сети Специальность 5В070200 Автоматизация и управление
• Анкор: Методические указания
• Дата: 21.01.2023
• Размер: 0.98 Mb.
• Имя файла: +Му к практ.работам всс.doc
• Тип: Методические указания; #897134
• страница: 5 из 10

Практическая работа№3

Принципы систолической обработки информации

Цель работы: Изучение принципов обработки информации в систолической системе.
Задачи:

1. Расписать процедуру умножения матриц А и В размерностью 3х3 в систолической системе.

2. Нарисовать схему умножения, составить таблицу и проверить экспериментально результат.
Краткая теория

Операция поиска вхождений с помощью линейной систолической структуры

Операция поиска вхождений заключается в том, что в некоторой исходной последовательности A=(a₁,a₂,...a_n), a_i=0 или 1, найти эталонную последовательность B=(b₁,b₂,...,b_m), причем b_j=0,1 или (*), где символом (*) обозначено безразличное состояние соответствующего разряда. Результатом операции является вектор R=(r_k), в котором каждый компонент r_i определяется по правилу:

r_i=1, если (b₁=a_i)(b₂=a_i+1)...(b_m=a_i+m), 0 в противном случае, где i=1,(n-m+1).

Для реализации этой операции используем ПЭ, способные выполнять поразрядное сравнение и сохранять результаты этого сравнения, соединив ПЭ в линейную конфигурацию. На входы каждого ПЭ поступают значения a_i и b_i; каждый ПЭ производит сравнение и запоминает частичный результат r, кроме того, по завершении сравнения синхронно с поступлением тактовых импульсов значения a_i и b_i передаются на входы следующих ПЭ, то есть:

a_вых(t)=a_вх(t-1) и b_вых(t)=b_вх(t-1), где t=1,2,.. – номер такта.

Пусть поиск вхождений производится для трехразрядного эталона–образца B=(b₁,b₂,b₃) в исходной последовательности A=(a₁,...a₅). На рисунке 7 показана временная диаграмма выполнения операции в систолической линейной матрице. На первом такте (t=1) значения a₁ и b₁ загружаются в ПЭ1 и ПЭ2 соответственно. На втором такте производится сдвиг a₁ и b₁ (соответственно в ПЭ2 и ПЭ4), на третьем - очередной сдвиг и загрузка a₂ и b₂ в ПЭ1 и ПЭ5 и т.д. На третьем такте в ПЭ3 попадают a₁ и b₁, где и производится их сравнение; результат сравнения r_ij(t) сохраняется в ПЭ3. Дальнейшее перемещение А и В по систолической структуре очевидно из диаграммы. На пятом такте в ПЭ3 попадают элементы a₂ и b₂, сравниваются там и вырабатывается результат r_i+1,_j+1(t+2); находится конъюнкция частичных результатов r(t+2)=r(t)r_i+1,_j+1(t+2), которая и сохраняется в ПЭ3. Первый окончательный результат – элемент r₁ вектора R – будет получен в ПЭ3 на седьмом такте в результате сравнения a₃и b₃. Второй элемент r₂ будет получен на восьмом такте, но в ПЭ4 и т.д.

Очевидно, что каждый ПЭ может выполнять операцию сравнения байтов или слов, что позволяет находить определенные последовательности в цепочках символов, то есть выполнять операции сравнения цепочек символов. Кроме того, осуществляя циклический сдвиг эталона - образца, может сократить число ступеней систолического конвейера, однако это приводит к дополнительным затратам времени. Отметим, что в рассматриваемой схеме ПЭ5 и ПЭ4 служат только для задержки элементов b_i, поэтому они могут быть заменены регистром сдвига.



Рисунок 7 - Реализация операции сравнения цепочек литер

Операция умножения квадратных матриц с помощью прямоугольной систолической матрицы.

Результат перемножения двух матриц C=AB формируется согласно формуле:



причем каждый элемент С=|c_ij| можно рассматривать как результат рекуррентных вычислений:

c_ij(0)=0; c_ij(k)=c_ij(k-1)+a_ikb_ik, k=1,n.

Такие суммы образуются при накапливании частичных сумм в процессе продвижения a_ij и b_ij по систолической матрице. Пусть обе матрицы A и B имеют размерность 2х2: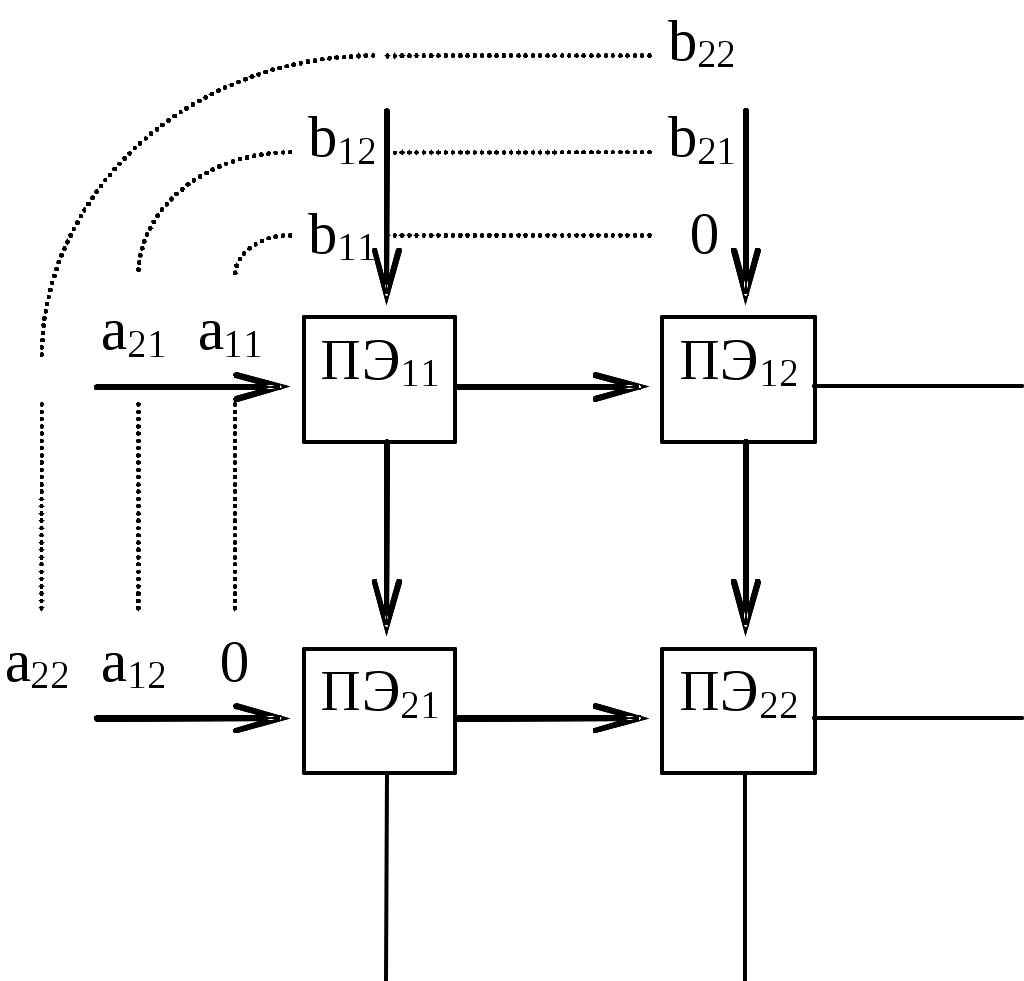





Рисунок 8 - Умножение матриц в систолической структуре

– и операция умножения производится с помощью ПЭ (рисунок 8), объединенных в прямоугольную матрицу. Загрузка элементов матриц А и В из памяти производится по строкам (А) и по столбцам (В) с характерным для систолической обработки сдвигом. Этот сдвиг (рисунок 8) обозначен 0.

В начальный момент все ПЭ установлены в исходное нулевое состояние. На первом такте в ПЭ11 загружаются элементы a₁₁ и b₁₁. На втором такте элементы a₁₁ и b₁₁ поступают на входы ПЭ12 и ПЭ21 соответственно. На ПЭ11 поступают a₂₁ и b₁₂ и в нем вычисляется сумма произведений a₁₁b₁₁+a₂₁b₁₂ (первое слагаемое этой суммы сохранено в ПЭ11 с первого такта). Одновременно в ПЭ12 и ПЭ21 вычисляются произведения a₁₂b₁₁ и a₁₁ и b₂₁ соответственно. Этот процесс продолжается, как показано в таблице. Весь процесс перемножения матриц требует 3n-2 шагов, где n – размерность перемножаемых матриц.

Такт	ПЭ11	ПЭ12	ПЭ21	ПЭ22
0	0	0	0	0
1	a11b11	0	0	0
2	c11	a11b21	a12b11	0
3		c12	c21	a12b21
4				c22

Здесь полезно вспомнить, что в последовательной ЭВМ перемножение матриц выполняется за n³ шагов, то есть достигаемое ускорение для систолической СОД составляет n³/(3n-2).