Методические указания к практическим работам. Методические указания к проведению практических занятий
 Скачать 452 Kb.
|
  (5)где  - статистическая вероятность отказа устройства на интервале ]t,t+t] или иначе - статистическая вероятность попадания на указанный интервал случайной величины Т; в нашем случае - (qi max) из задания 2.Р(t)- рассчитанная в задании 1 -вероятность безотказной работы устройства. Напомним, что значение t определяется из табл.2, а принятое в работе значение t=3*103 ч. Если интенсивность отказов не меняется в течение всего срока службы объекта, т.е. (t) = = const, то наработка до отказа распределена по экспоненциальному (показательному) закону. В этом случае вероятность безотказной работы блока  (6)а средняя наработка блока до отказа находится как  . (7)При последовательном соединении k блоков интенсивность отказов образуемой ими подсистемы:  . (8)Если интенсивности отказов всех блоков одинаковы, то интенсивность отказов подсистемы П = k, (9) а вероятность безотказной работы подсистемы Рп(t) = exp(-Пt)= exp(- kt). (10) С учетом (7) и (8) средняя наработка подсистемы до отказа находится как  . (11)Для расчета значений РБ(t) и РП(t) интервал наработки t примите равным 400ч. Постройте график как точечный, установив максимальное значение t=5200 ч, при вычислении РП(t) расчеты можно прекратить, достигнув значения 0,05. Соотношения (8) и (9) справедливы для экспоненциального распределения. Для любого распределения наработки до отказа вероятность безотказной работы подсистемы, состоящей из k последовательно соединенных блоков, связана с вероятностями безотказной работы этих блоков следующим соотношением:  . (12)Если блоки равнонадежны, как принято в задании, то  . (13)Рассчитав значение РП(t) по формуле (13) для  , сравните его со значением, рассчитанным по формуле (6) и сделайте вывод о надежности блока и подсистемы.Контрольный вопрос. В какой период эксплуатации - начальный или по мере приближения к предельному состоянию - интенсивность отказов объектов обычно резко и неуклонно возрастает, и почему? Задание 4. Для наработки  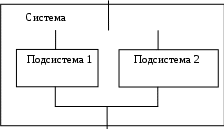требуется рассчитать вероятность безотказной работы Рс( ) системы (рис.3), состоящей из двух подсистем, одна из которых является резервной.   Рис.3 Схема системы с резервированием Методические указания к заданию 4. Расчет ведется в предположении, что отказы каждой из двух подсистем независимы, т.е. отказ первой системы не нарушает работоспособность второй, и наоборот. Вероятности безотказной работы каждой системы одинаковы и равны РП  . Тогда вероятность отказа одной подсистемы QП = 1-PП Вероятность отказа всей системы  определяется из условия, что отказала и первая, и вторая подсистемы, т.е. = QП * QП =  .Отсюда вероятность безотказной работы системы Рс( )=1- или иначе Рс( )=1-(1- РП )2 Требуется рассчитать вероятность отказа системы и подсистемы при наработке Тп , сравнить их и сделать вывод о надежности. Контрольный вопрос. Какие недостатки Вы видите в принятой схеме резервирования? Задание 5. По данным табл.6 требуется определить зависимости от наработки (пробега автомобиля) математического ожидания (среднего значения) износа шатунных шеек коленчатого вала ДВС y(t) и дисперсии износа Д(y(t)) , полученные уравнения необходимо записать. Параметры искомых зависимостей следует рассчитать с использованием правила определения уравнения прямой, проходящей через две точки с известными координатами. Методические указания к заданию 5. Данное задание выполняется в предположении, что математическое ожидание (среднее значение) и дисперсия износа шатунных шеек коленчатого вала представляют собой линейные функции пробега автомобиля. Это подтверждается исследованиями, проведенными в различных автохозяйствах и обработкой статистических данных. Обозначим износ шеек как некоторую переменную величину Y. Зависимость Y от наработки (пробега автомобиля) представляет собой случайную функцию, реализации которой являются монотонными неубывающими функциями. Для описания такой случайной функции часто вполне достаточно знать, как меняются в зависимости от наработки ее математическое ожидание (среднее значение) и дисперсия: y(t) и Д(y(t)). Исследования, проведенные в различных автохозяйствах, показывают, что для описания зависимости износа от пробега автомобиля могут быть использованы линейные функции y(t) = y0 + аt, (в мм) (14) Д(y(t)) = Д(y0) + вt, (в мм2) (15) где y0 и Д(y0) соответственно - среднее значение и дисперсия износа шеек при t=0, при этом началом отсчета является последняя обточка коленвалов; а - средняя скорость увеличения износа, мм/тыс.км; в - скорость увеличения дисперсии износа, мм2/тыс.км; t - пробег автомобиля, тыс.км. Таблица 6 Результаты обработки измерения износа шатунных шеек коленчатых валов двигателя автомобиля.
Примечание, Обратите внимание на размерность дисперсии- (10-3) Искомыми параметрами функций (14) и (15) являются y0, а, Д(y0) и в. На практике для их нахождения необходимо область возможных значений наработки (нижняя граница которой t=0, а верхняя находится из условия достижения предельного значения износа) разбить на несколько (обычно 10-20) интервалов. При каждом из разделяемых этими интервалами пробегов автомобиля t1, t2, ..., ti, ... производят измерения износа большого количества коленчатых валов и вычисляют соответствующие пробегам средние значения y1, y2, ..., yi, ..., а затем дисперсии Д(y1), Д(y2), ..., Д(yi), .... Располагая такими наборами значений ti и yi или ti и Д(yi), можно, используя метод наименьших квадратов, определить искомые зависимости y(t) и Д(y(t)). В контрольной работе задача существенно упрощена. Предполагается, что массивы данных об износе шеек для каждого ti уже обработаны. Считается также возможным определить искомые линейные зависимости, располагая координатами только двух точек. В таком случае параметры а и в зависимостей (14) и (15) могут быть определены соответственно  (16)и  (17)После этого, используя координаты любой из известных двух точек, например, второй (t2, y2) или (t2,Д(у2)), можно найти два других параметра  ; (18) (19)Произведите необходимые вычисления и запишите полученные выражения (14) и (15) с числовыми значениями параметров. Сформулируйте вывод по контрольному вопросу. Контрольный вопрос. Могут ли исходные значения среднего износа шеек у0 и дисперсии износа Д(у0), соответствующие t=0, быть равными 0? Отрицательными числами? Задание 6. Требуется рассчитать средние значения {y(ti)}, дисперсии {Д(y(ti))} и средние квадратические отклонения {(y(ti))} износа при нескольких значениях пробега, пользуясь зависимостями, полученными в предыдущем задании. Затем требуется для тех же значений пробега определить нижнюю y(ti)min и верхнюю y(ti)max границы практически возможных значений износа. Результаты расчетов следует занести в таблицу, выполненную по форме табл.7, и построить по ним линии, представляющие собой зависимость среднего износа шеек от пробега, нижнюю и верхнюю границы практически возможных значений износа. Таблица 7 Результаты расчета средних значений, дисперсий и средних квадратических отклонений износа шеек коленчатых валов.
Предельное значение упр износа шеек коленчатых валов ДВС типа ЧН21/21 установлено равным 0,15мм. Заданный пробег указан в табл.8. Таблица 8 Заданная серия и пробег Тзад
Методические указания к заданию 6. Заполните таблицу, последовательно производя вычисления по формулам, полученным при выполнении задания 5, для различных значений пробега автомобиля. Расчет среднеквадратических отклонений произведите по формуле  ,где i- номер интервала в табл.7. Для нахождения области практически возможных значений случайной величины Yi, распределенной по нормальному закону, пользуются “правилом трех сигма”. В соответствии с этим правилом для каждого пробега автомобиля ti верхняя и нижняя границы практически возможных значений износа шеек находятся как | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||