Методические указания к практическим работам. Методические указания к проведению практических занятий
 Скачать 452 Kb.
|
Методические указания к проведению практических занятийЗадание 1. В табл.2 приведены значения наработок до отказа в находившейся под контролем партии топливных форсунок дизелей автомобилей. Таблица 2 Значения наработки устройства до отказа и заданные значения t0 и T0.
Требуется определить статистические вероятности безотказной работы Р(t) и отказа Q(t) устройства для заданного значения t, указанного в табл.2. Далее необходимо рассчитать значение вероятности безотказной работы P*(t) по первым 20 значениям наработки до отказа, указанным для соответствующего варианта в табл.2. Затем для заданной наработки t требуется рассчитать математическое ожидание числа работоспособных устройств Np(t) при общем числе находившихся в эксплуатации форсунок, указанном в табл.3. Таблица 3 Объем партии устройств и заданное значение к
При выполнении расчетов возможно использование обычного калькулятора, что увеличивает трудоемкость расчетов, или использовать универсальное приложение MicrosoftOffice – MicrosoftEcxel любой версии для ПЭВМ. При этом Ecxel рекомендуется использовать для расчетов и построения необходимых графиков. Методические указания к заданию 1. Наработка исследуемых топливных форсунок до отказа есть непрерывная случайная величина Т. По результатам испытания (наблюдения и эксплуатации) партии из N устройств получена дискретная совокупность из N значений t1, …, ti, …, tN, указанных в табл.2. Статистически вероятность безотказной работы устройства для наработки t определяется как  (1)где Np(t) - число объектов, работоспособных на момент времени t. Для определения Np(t) из табл.2 следует выбрать значения Т, превышающие t. На этом этапе рекомендуется перенести значения массива чисел согласно своему варианту из таблицы 2 в столбец А приложения Ecxel, далее копировать этот массив в столбец В и упорядочить значения по возрастанию. При выполнении расчетов необходимо быть очень внимательным, поскольку полученные результаты используются в последующем, и ошибка на первом шаге приводит к неверным результатам всех последующих вычислений. Вероятность отказа устройства за наработку t статистически определяется как  (2)где Nнр(t) - число объектов, неработоспособных к наработке t. Для определения Nнр(t) из табл.2 следует выбрать значения Т, меньшие t., или из столбца В число значений, расположенных выше значения t. Поскольку Np(t) + Nнр(t) = N, нетрудно видеть, чему равна сумма вероятностей: P(t) + Q(t). Подсчет этой суммы используйте для проверки правильности своих вычислений. Оценку вероятности безотказной работы устройства по первым 20-ти значениям наработки до отказа обозначим как P*(t). Ее значение определяется также по формуле (1), но при этом N = 20, и число работоспособных объектов Np(t) выбирается из этой совокупности. При использовании ПЭВМ рекомендуется перенести первые 20 значений из столбца А в столбец С и упорядочить их. Будем считать, что условия опыта, включающего 50 наблюдений, позволили однозначно определить вероятность безотказной работы форсунки, т.е. P(t) = 1 - F(t). Здесь F(t) - функция распределения случайной величины “наработка до отказа”, определяющая вероятность события T t при N . Тогда с учетом формулы (1) математическое ожидание числа объектов  , работоспособных к наработке t, определяется как  где N - объем партии устройств, определяемый по табл.3. Контрольный вопрос. Чем объясняется возможное различие значений P(t) и P*(t) ? Задание2. Требуется рассчитать среднюю наработку до отказа Т рассматриваемых форсунок. Первоначально вычисления произвести непосредственно по выборочным значениям Т, указанным в табл.2, а затем с использованием статистического ряда. Методические указания к заданию 2. Для вычислений среднего значения Т случайной величины Т непосредственно по ее выборочным значениям t1, t2, …, ti, …, tN используют формулу  (3)Уточним, что здесь N равно числу значений Т в табл.2 для заданного вам варианта. Ошибки, которые можно сделать при расчетах, разделяют на технические и методические. Техническая ошибка является следствием неправильных действий вычислителя (ошибка при введении числа в калькулятор, повторное введение одного и того же числа, пропуск одного или нескольких чисел и т.п.). Методическая ошибка определяется используемым методом и формулами расчета. Формула (3) не несет в себе методической ошибки, однако расчеты с ее помощью обычно трудоемки и часто приводят к неверным результатам в силу технических ошибок при использовании больших массивов чисел и калькуляторов. Значительно упростить и ускорить вычисления можно путем использования преобразования результатов наблюдений (совокупности значений t i ) в статистический ряд. С этой целью весь диапазон наблюдаемых значений Т делят на m интервалов или “разрядов” и подсчитывают число значений ni, приходящихся на каждый i-ый разряд. Результаты такого подсчета удобно записывать в форме, соответствующей табл.4. Таблица 4 Преобразование значений наработки до отказа в статистический ряд (пример)
Длины t всех разрядов чаще всего принимают одинаковыми, а число разрядов m обычно рассчитывается по формуле в зависимости от количества элементов массива (вариационного ряда). Для выполнения данного задания примите t = 3*103ч., а m = 4. Для примера в табл.4 указаны результаты систематизации в виде статистического ряда 100 значений случайной величины, распределенной на интервале ]8,5*103ч; 20,5*103ч] для тех же условий, т.е. t = 3*103ч., m= 4. Заполнять таблицу несложно. Сделайте заготовку таблицы. Определите границы интервалов (разрядов). Последовательно просматривая массив значений {ti} (столбец В ), оценивают, к какому разряду относится каждое число. Затем подсчитывают n1, …, ni,…, nm - число попаданий значений случайной величины соответственно в 1-ый, …, i-ый,…, m-ый разряд. Правильность подсчетов определяют, используя следующие соотношения:  Н  ижнюю границу интервала То установите, пользуясь табл.2.Статистический ряд можно отразить графически, как показано на рис.1. 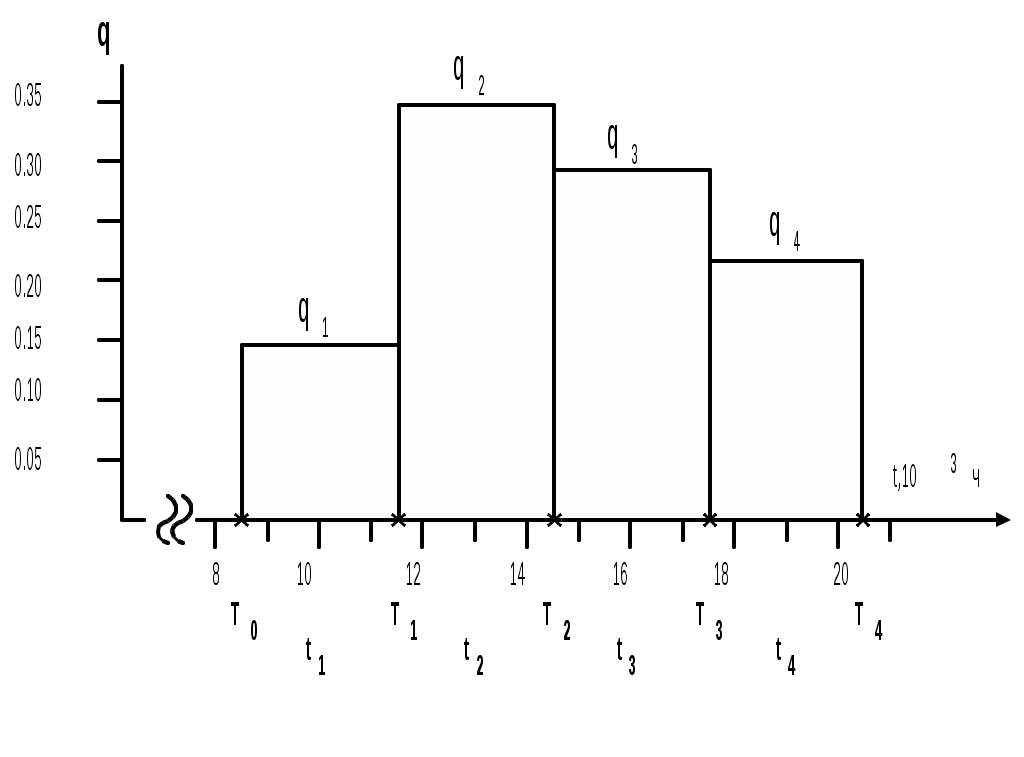 Рис.1. Статистический ряд С этой целью по оси абсцисс отложите разряды и на каждом разряде постройте прямоугольник, высота которого равна статистической вероятности попадания случайной величины на данный интервал. Здесь T1, …, Ti, …, Tm соответственно верхние границы 1‑го, …, i-го, …, m-го интервалов, определяемые принятыми значениями Т0 и t. Статистическая вероятность qi попадания случайной величины на i-ый интервал рассчитывается как  Определите максимальное значение qi, и запомните его как qi max Подсчитайте значения qi для всех разрядов и проверьте правильность расчетов, используя выражение  Для расчета среднего значения случайной величины в качестве “представителя” всех ее значений, принадлежащих i-му интервалу, принимают его середину  . Тогда средняя наработка до отказа определяется как  (4)Расчет с использованием формулы (4) вносит некоторую методическую ошибку. Однако ее значение обычно пренебрежимо мало. Эту ошибку в Ваших расчетах оцените по формуле  где  и  - средние значения, вычисленные соответственно с использованием формул (3) и (4).Контрольныйвопрос. Каким образом можно уменьшить ошибки в расчетах с использованием второго метода? Задание3. Требуется рассчитать интенсивность отказов (t) для заданных значений t и t. Затем в предположении, что безотказность некоторого блока в электронной системе управления автомобиля характеризуется интенсивностью отказов, численно равной рассчитанной, причем эта интенсивность не меняется в течение всего срока его службы, необходимо определить среднюю наработку до отказа ТБ такого блока. Подсистема управления включает в себя k последовательно соединенных электронных блоков (рис.2). 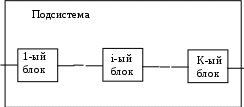 Рис.2 Подсистема управления с последовательно включенными блоками Эти блоки имеют одинаковую интенсивность отказов, численно равную расчитанной. Требуется определить интенсивность отказов подсистемы П и среднюю наработку ее до отказа ТП , построить зависимости вероятности безотказной работы одного блока РБ(t) и подсистемы РП(t) от наработки и определить вероятности безотказной работы блока РБ(t) и подсистемы РП(t) к наработке t=ТП. Значение k указано в табл.3. Методические указания к заданию 3. Интенсивность отказов (t) рассчитывается по формуле | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||