Газовые циклы. Методические указания к расчетнографическим работам для студентов iiiii курсов фла
 Скачать 1.94 Mb. Скачать 1.94 Mb.
|
1 2 3. Энтропия Энтропией называется функция, определяемая выражением Энтропия так же, как внутренняя энергия и энтальпия, является функцией параметров состояния, и ее изменение не зависит от процесса. Поэтому Энтропия является экстенсивной характеристикой вещества и где Размерность удельной энтропии из (38, 39) – Начало отсчета энтропии является условным, так как при рассмотрении термодинамических процессов определяется изменение энтропии в процессе, т. е. разность энтропии в начальном и конечном состоянии системы. Термодинамическая температура 4. Термодинамические процессы Термодинамическим процессом называется совокупность последовательных изменений параметров состояния системы. Графически можно представить только равновесные термодинамические процессы. Термодинамические процессы, в которых один из параметров состояния не изменяется, называются частными. Процесс, в котором не изменяется объем (удельный объем), называется изохорным. Для изохорного процесса следовательно, для любых состояний системы Линии, изображающие изохорный процесс на термодинамических диаграммах, называются изохорами. Вид изохор идеального газа показан на рис. 4. Так как  а б в Рис. 4. Изохоры идеального газа Теплота в изохорном процессе из так как С учетом для конечного процесса 1-2 Изменение энтальпии в изохорном процессе 1-2 с учетом (37) Изменение энтропии в изохорном процессе 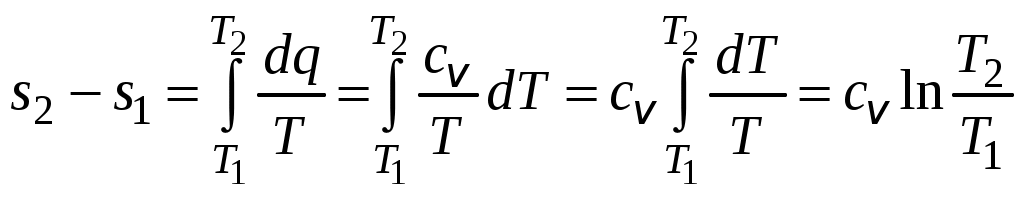 . (48) . (48)Процесс, в котором не изменяется давление, называется изобарным Из уравнения состояния идеального газа следовательно, Линии, изображающие на термодинамических диаграммах изобарный процесс, называются изобарами. Вид изобар идеального газа показан на рис. 5. 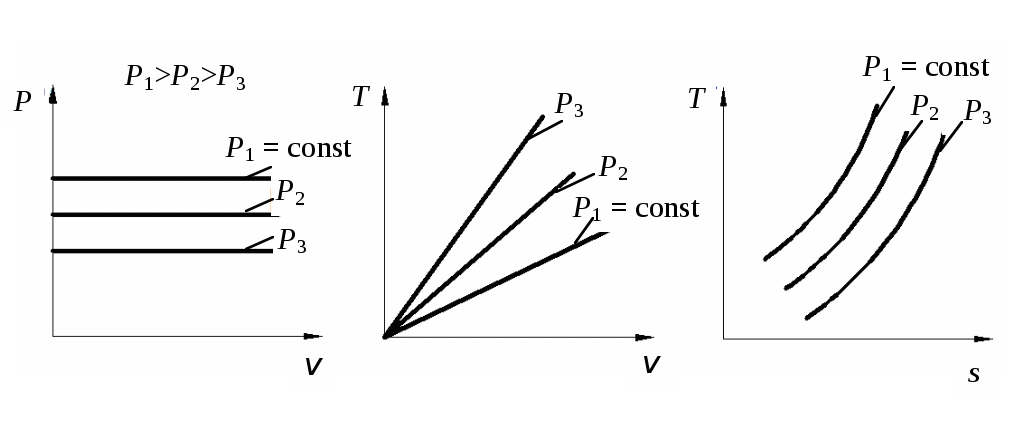 а б в Рис. 5. Изобары идеального газа Работа расширения в изобарном процессе 1-2 или Для изобарного процесса Для конечного процесса 1-2 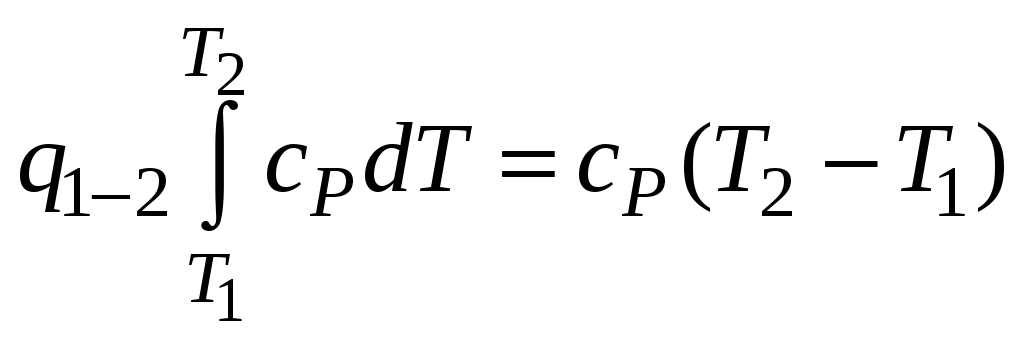 . (54) . (54)Изменение энтальпии Изменение внутренней энергии Изменение энтропии 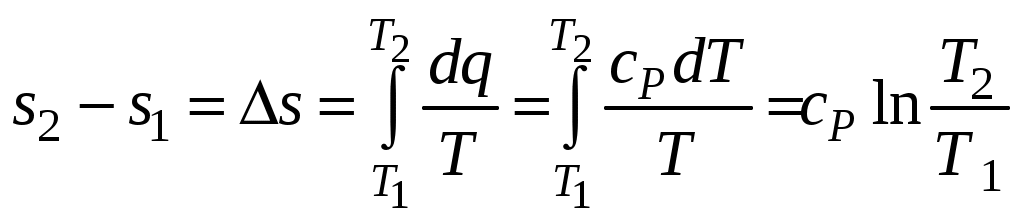 . (57) . (57)Термодинамический процесс, в котором не изменяется температура, называется изотермическим Для идеального газа в изотермическом процессе следовательно, Линии, изображающие изотермический процесс, называются изотермами. Вид изотерм идеального газа показан на рис. 6. Работа расширения в изотермическом процессе 1-2 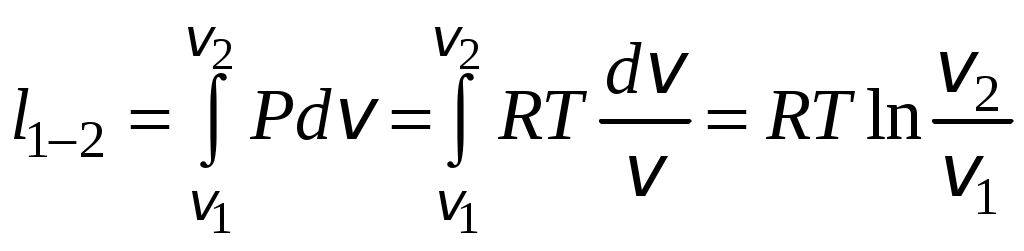 . (60) . (60)С учетом уравнения состояния идеального газа выражение (60) можно представить в виде  а б в Рис. 6. Изотермы идеального газа Запишем или Для изотермического процесса или Для конечного процесса 1-2 Изменение внутренней энергии в изотермическом процессе Теплоемкость в изотермическом процессе Адиабатным называется процесс, в котором к системе не подводится и не отводится тепло, Уравнение адиабатного процесса где Следовательно, для адиабатного процесса На основании (72) и уравнения состояния для адиабатного процесса 1-2 можно получить 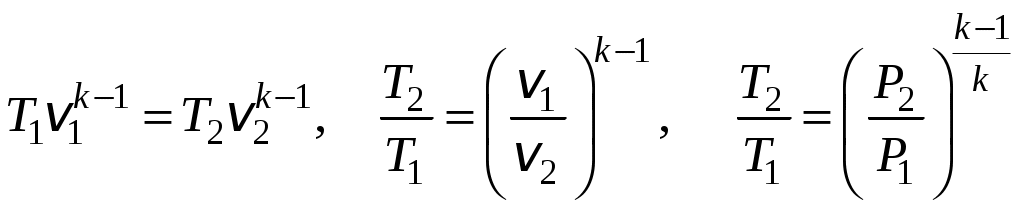 . (73) . (73)Работа расширения в адиабатном процессе из тогда Для конечного процесса 1-2 Из уравнения адиабаты тогда работа расширения 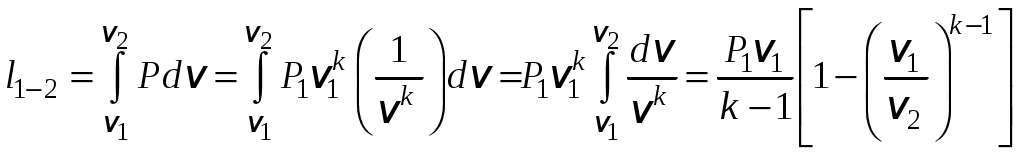 , (76) , (76)или через давление  . (77) . (77)С учетом соотношения (73) уравнение (77) принимает вид или или С учетом (74) работа расширения и соответственно внутренняя энергия 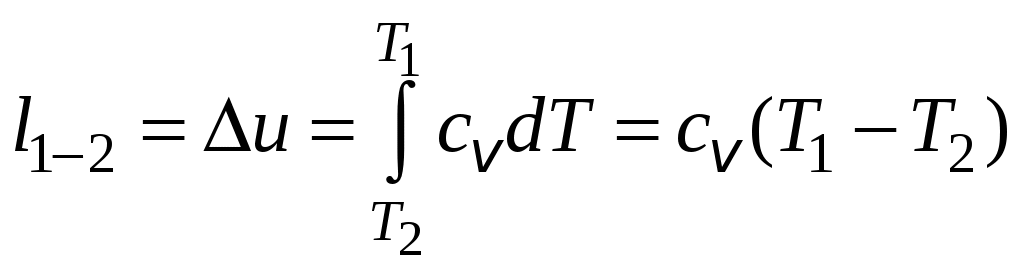 . (81) . (81)Изменение энтальпии в адиабатном процессе Теплоемкость адиабатного процесса 5. Политропные процессы Политропными называются процессы, удовлетворяющие уравнению Величина Теоретически отсюда 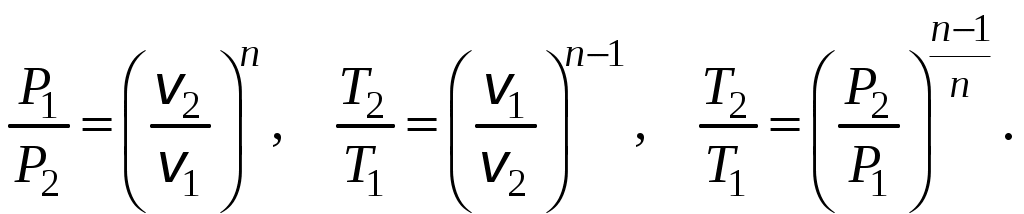 (85) (85)Работа расширения в политропном процессе (по аналогии с адиабатным процессом): 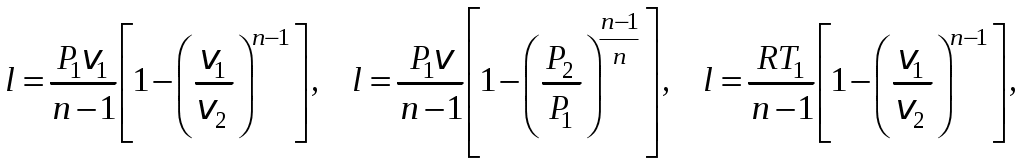 Количество тепла в политропном процессе из где С учетом формулы Майера и соотношения Исходя из общего определения теплоемкости, можно заключить, что в (88) где Понятие политропного процесса позволяет обобщить все частные термодинамические процессы. Так при Запишем уравнение политропного процесса в виде тогда при При Если показатель политропы Изменение энтропии в политропных процессах 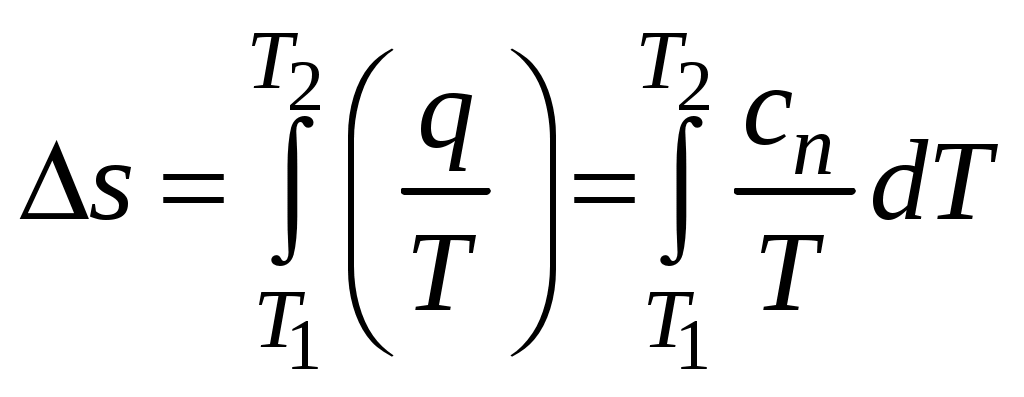 , (96) , (96)если 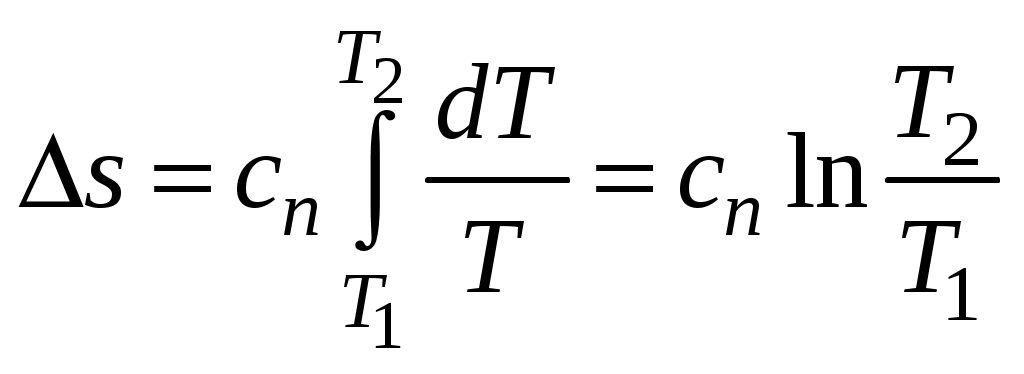 . (97) . (97)6. Термодинамические циклы В процессе расширения газ совершает работу против сил внешнего давления, которую можно превратить в механическую работу. Но этот процесс ограничен конечным давлением, до которого можно осуществлять расширение газа. Для того чтобы создать машину, производящую механическую работу непрерывно, необходимо возвратить газ в исходное состояние и вновь повторить процесс расширения. При этом газ совершает круговой процесс (цикл), состоящий из последовательных процессов расширения и сжатия. На сжатие газа необходимо затратить какую то работу от внешнего источника. Очевидно, что работа расширения должна быть больше, чем работа сжатия, только тогда суммарная работа будет больше нуля. Схема такого цикла приведена на рис. 7 в 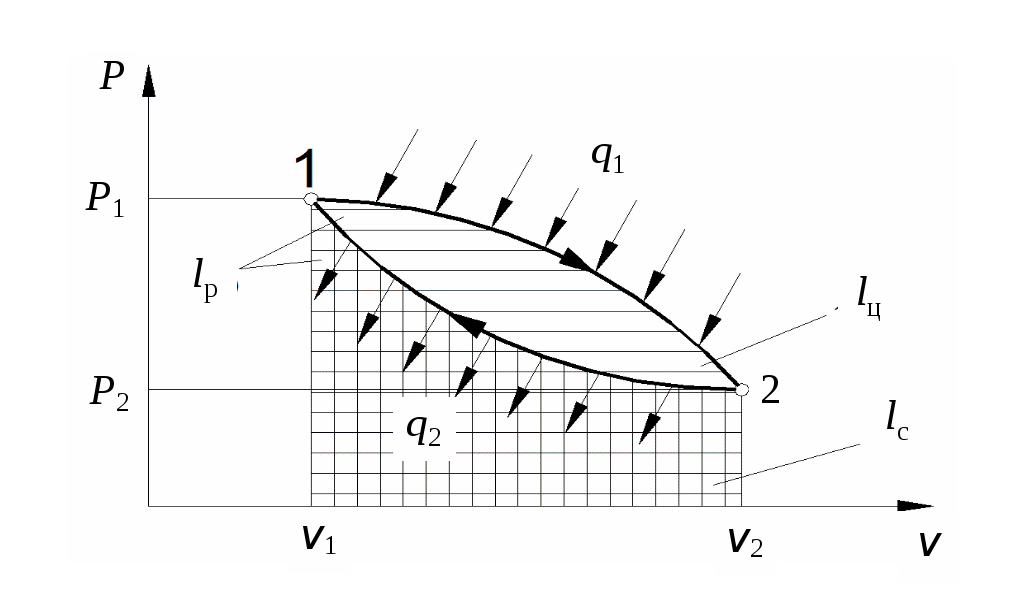 Рис. 7. Схема термодинамического цикла Процесс расширения протекает по кривой 1-2 от давления Процесс сжатия происходит по кривой 2-1 от давления Очевидно, что суммарная работа равна площади, ограниченной процессами цикла (1-2-1). Эта работа может быть реализована в механическую работу и называется работой цикла. где Циклические процессы, в результате которых производится работа, реализуется в тепловых двигателях. Тепловым двигателем называется непрерывно действующая система, осуществляющая круговые процессы (циклы), в которых тепло превращается в работу. Вещество, за счет изменения состояния которого получается работа в цикле, называется рабочим телом. Для того чтобы тепловой двигатель производил работу, необходимо, чтобы кривая процесса расширения рабочего тела располагалась выше кривой процесса сжатия (рис. 7). Это возможно только в том случае, если в процессе расширения к рабочему телу подводить тепло. В соответствии со вторым законом термодинамики для создания теплового двигателя необходимо часть тепла отводить от рабочего тела в окружающую среду в процессе сжатия. Обозначим количество тепла, подводимого к 1 кг рабочего тела, Таким образом, общий принцип работы теплового двигателя можно представить следующим образом. При давлении Если направление процессов, составляющих цикл, происходит по направлению часовой стрелки, как показано на рис. 7, то такие циклы называются прямыми. Работа тепловых двигателей основана на прямых термодинамических циклах. Термодинамический цикл можно реализовать и в противоположном направлении, против часовой стрелки (рис. 8). 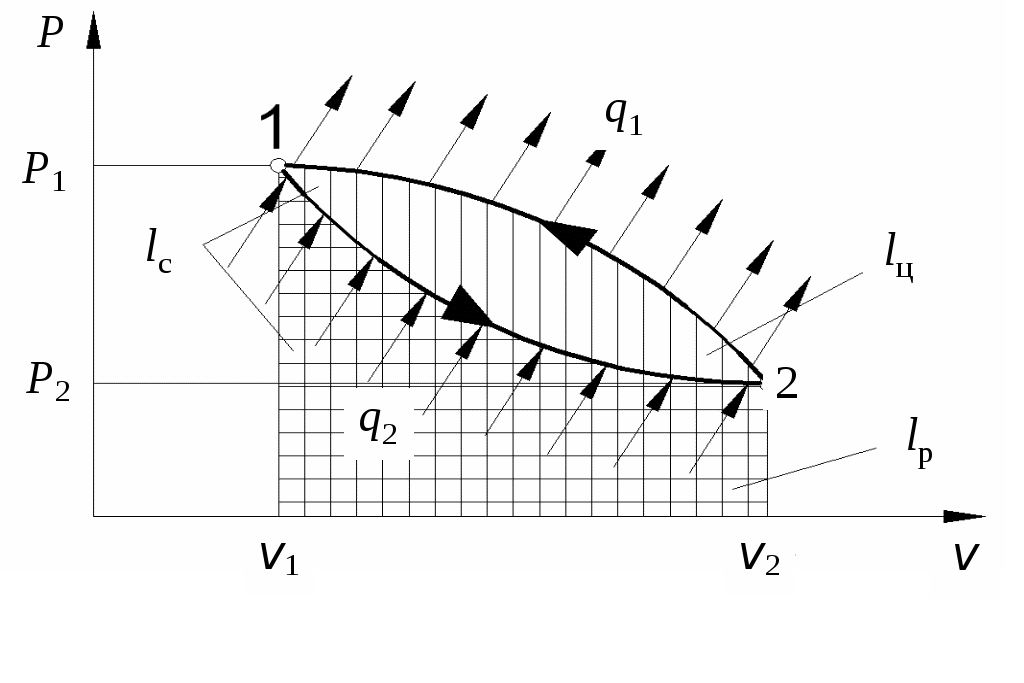 Рис. 8. Обратный термодинамический цикл Такой цикл называется обратным термодинамическим циклом. В обратном цикле кривая расширения рабочего тела лежит ниже кривой сжатия, следовательно, суммарная работа цикла отрицательна, т.е. для его осуществления необходимо затратить работу. Но при этом рабочее тело будет воспринимать тепло Самопроизвольный перенос тепла в природе может осуществляться только с более высокого температурного уровня на более низкий. Согласно одной из формулировок второго закона термодинамики «теплота на может сама собой переходить от более холодного тепла к более нагретому». Обратный цикл не нарушает второй закон термодинамики. Для того чтобы перенести тепло от холодного источника к горячему, необходимо затратить работу. В соответствии с законом сохранения энергии: В обратном цикле «горячему источнику» будет передаваться тепло Степень совершенства термодинамических циклов характеризуется термическим коэффициентом полезного действия. Для прямых циклов термический КПД характеризует, какое количество работы можно получить на единицу подводимого тепла: или Чем больше Степень совершенства обратных термодинамических циклов характеризуется холодильным коэффициентом. Холодильный коэффициент характеризует, какое количество тепла можно отвести от холодного источника на одну единицу затраченной работы: Чем больше 7. Задание к расчетно-графической работе Для заданного газового цикла, отнесенного к 1 кг воздуха, требуется: определить параметры построить цикл в масштабе в координатах найти определить расчетом теплоту определить графическим методом по 8. Методические указания к выполнению РГР Цикл отнесен к 1 кг воздуха. В рассмотренном в заданиях диапазоне давлений и температур воздух можно считать с достаточной для технических расчетов точностью идеальным газом и использовать для расчетов зависимости для идеальных газов. Для простоты расчетов теплоемкость следует принять постоянной, не зависящей от температуры: Газовая постоянная воздуха Для расчета параметров состояния точек цикла воспользуемся уравнением состояния и уравнениями процессов. Пример расчета Задан цикл, изображенный на рис. 9. 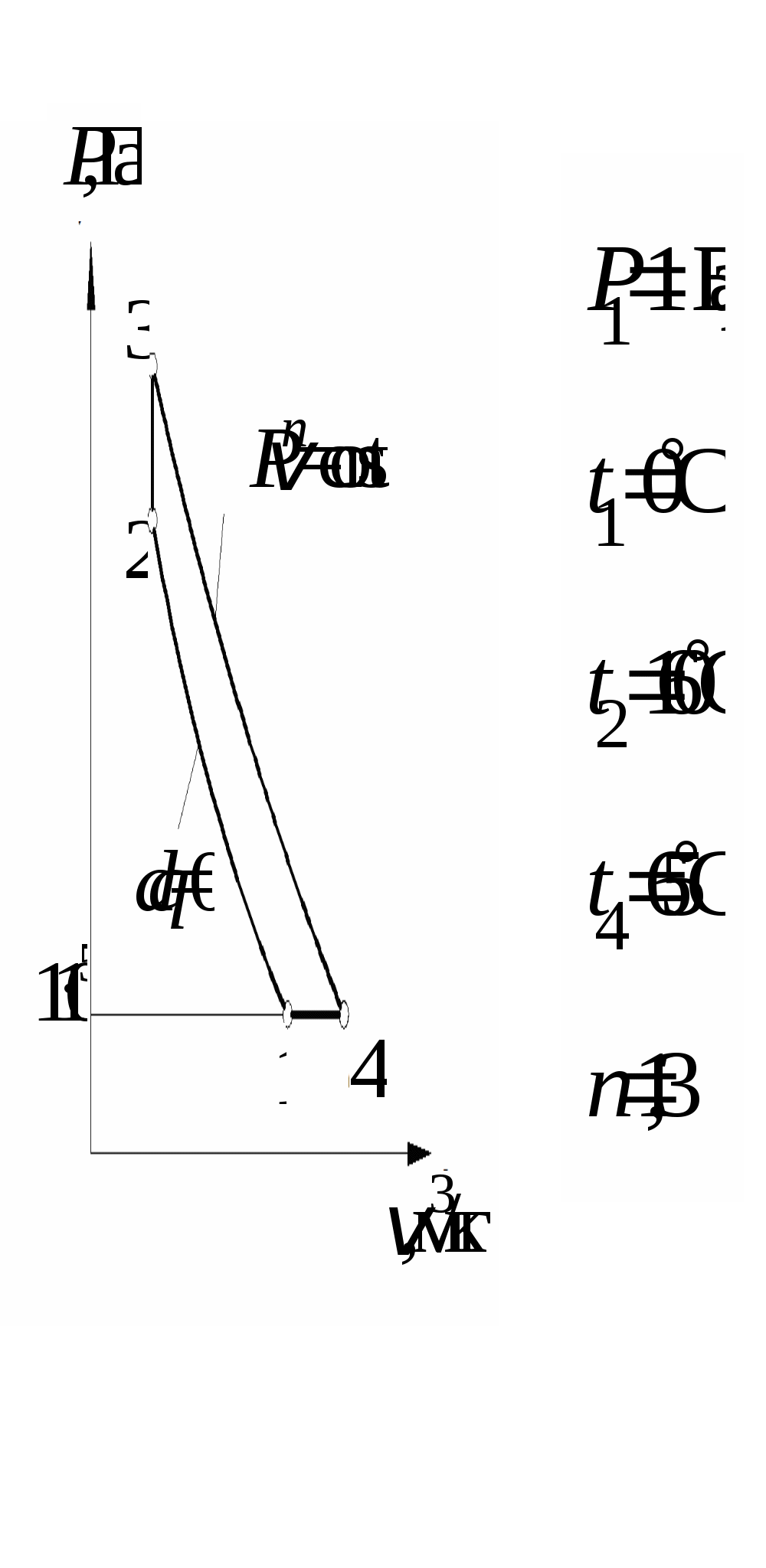 Рис. 9. Исходные данные для расчета цикла Для точки 1 известно Температуру Для точки 2 известно можно получить где отсюда  , ,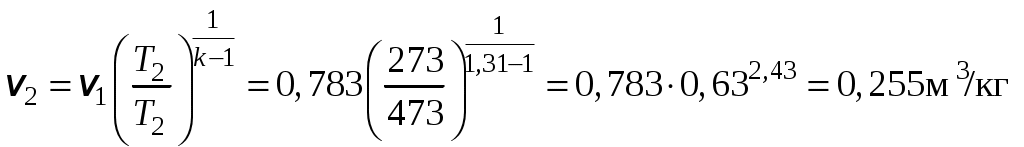 . .Из уравнения состояния давления Внутренняя энергия и энтальпия точки 2: Для точки 4 известно Из уравнения состояния: Для точки 3 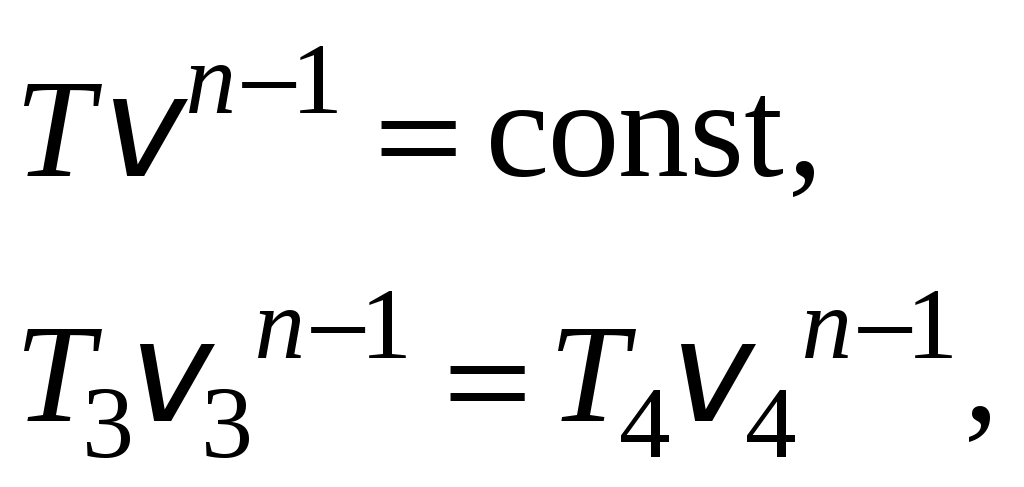 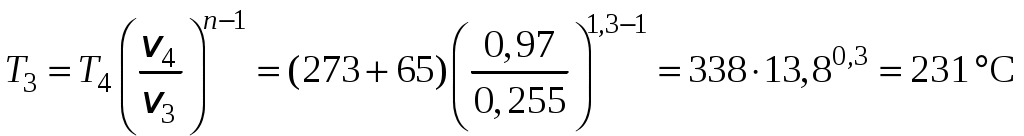 . .Тогда давление в точке 3: Результаты расчетов сведем в табл. 1. Т а б л и ц а 1
Для построения цикла в масштабе необходимо сначала построить цикл в координатах 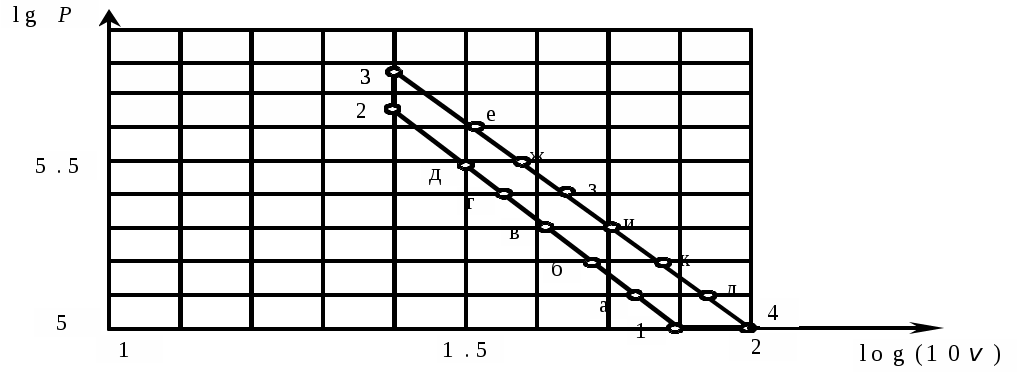 Рис. 10. Газовый цикл в логарифмических координатах Адиабаты (1-2) и политропа (3-4) в логарифмических координатах представляют прямые линии. На них произвольно откладываются промежуточные точки (а-л), для которых из графика определяются значения Аналогичным образом выполняется построение цикла в Определим для каждого процесса цикла Работа процесса из Для изохорного процесса 2-3: Для политропного процесса 3-4: Работу процесса определим из Для изобарного процесса 4-1: Результаты расчетов следует снести в табл. 2. Т а б л и ц а 2
По результатам расчетов изменения энтропии в процессах цикла построить цикл в координатах Определим количество тепла, подведенного к рабочему телу в цикле: Определим термический КПД цикла: 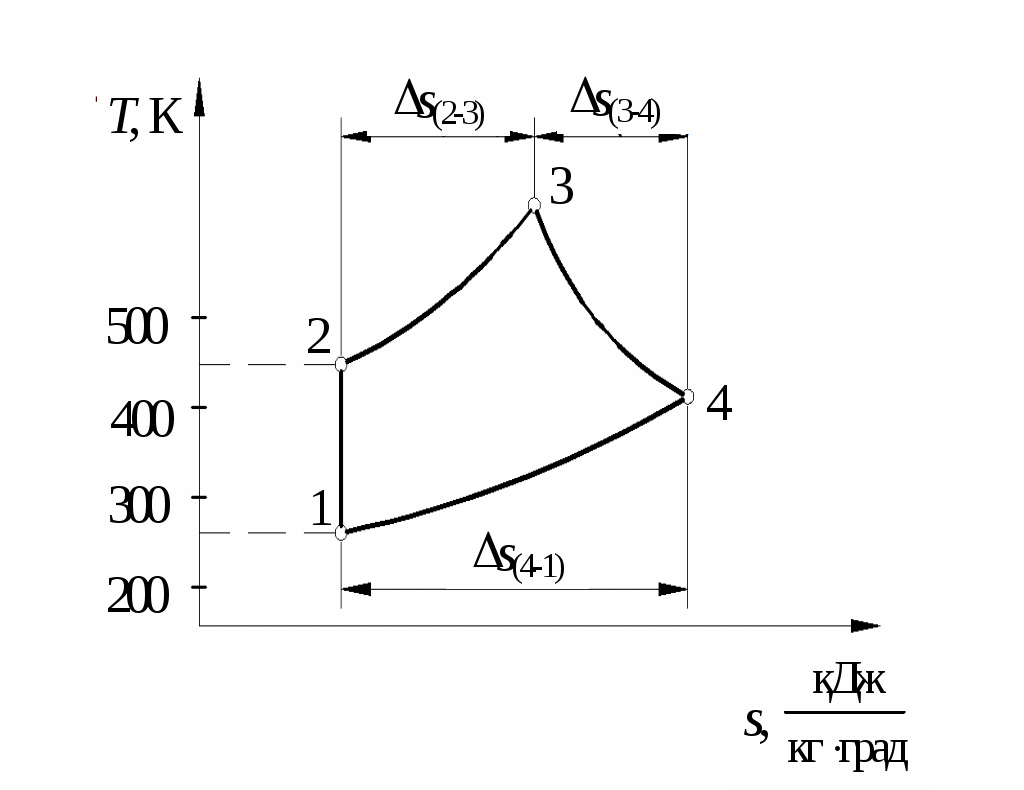 Рис. 11. Расчетное значение КПД цикла проверяется графически. Для этого по Масштабный коэффициент Подводимая теплота цикла Масштабный коэффициент Графически КПД цикла определяется как  . .Расхождение между теоретическим и графическим значениями КПД цикла не должно превышать 10 %. Варианты заданий 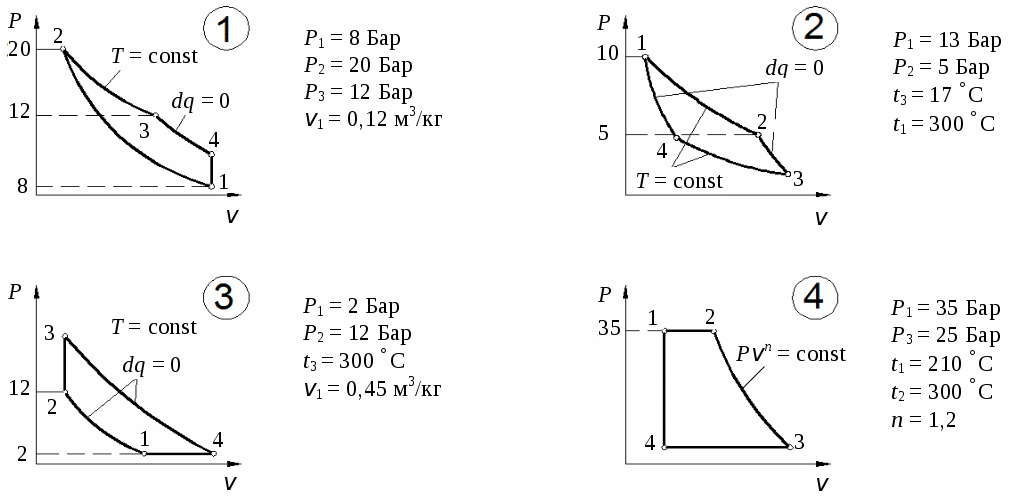 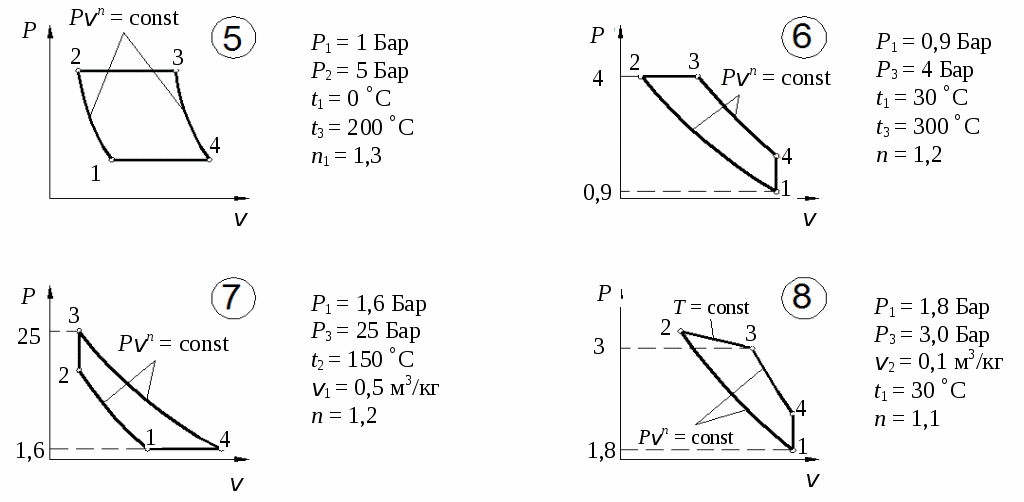 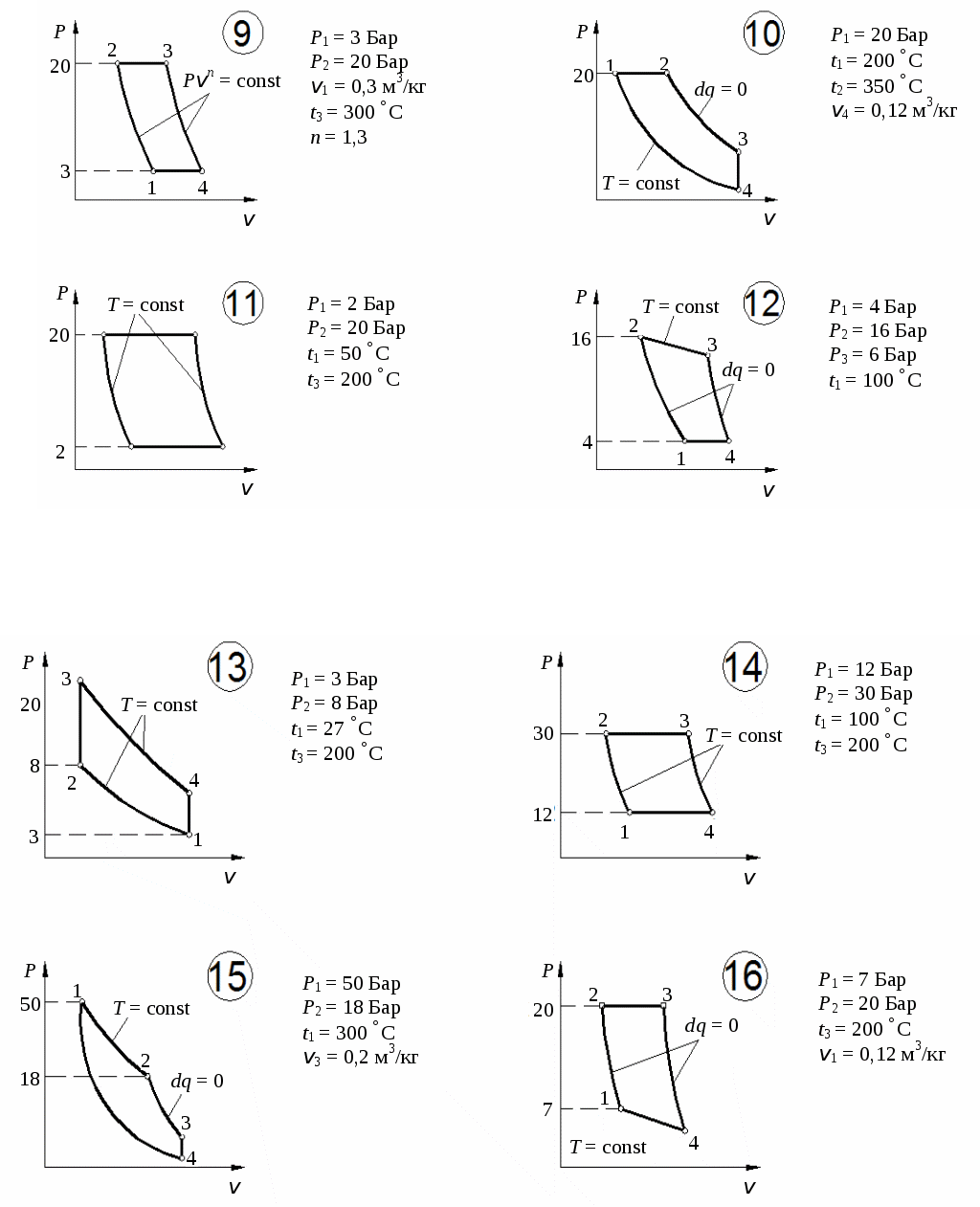 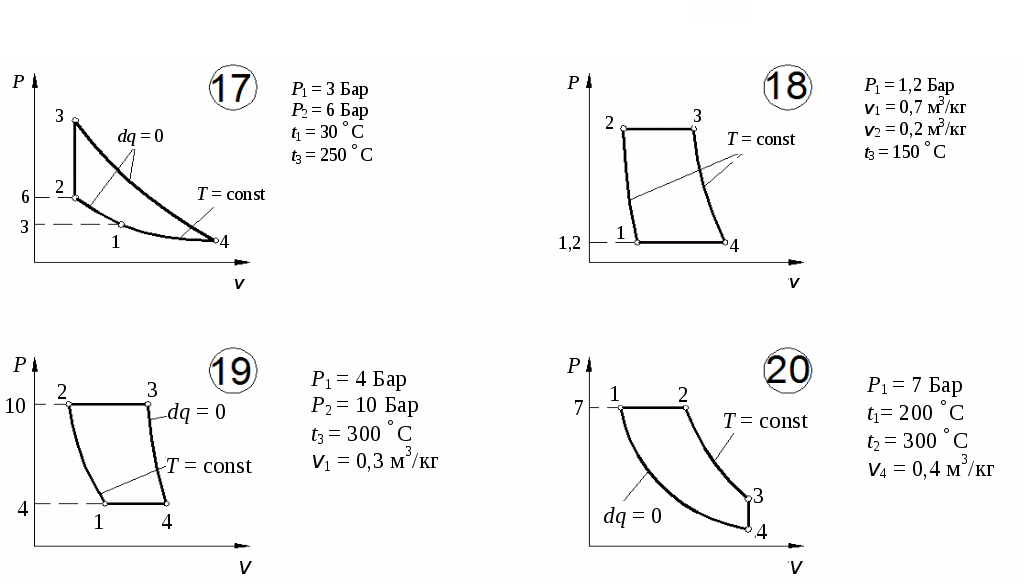  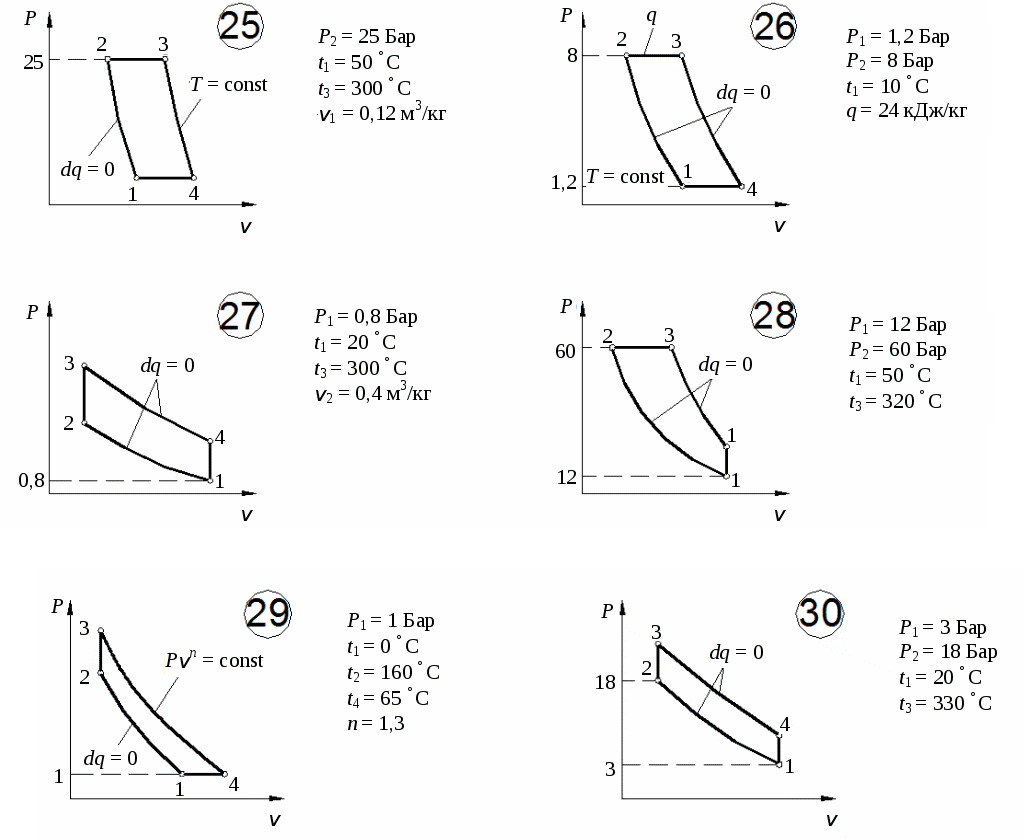 Список литературы 1. Болгарский А.В. и др. Термодинамика и теплопередача. – М.: Высшая школа, 1975. 2. Болгарский А.В. и др. Сборник задач по термодинамике и теплопередаче. – М.: Высшая школа, 1972. 3. Кругов В.И. Техническая термодинамика. – М.: Высшая школа, 1971.  ГАЗОВЫЕ ЦИКЛЫМетодические указания | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 тпечатано в типографии
тпечатано в типографии