Русча методичка ХГИ. Методические указания к выпольнению расчетнографических работ по предмету электротехника и основы электроники
 Скачать 1.59 Mb.
|
3-задание. Расчёт трёхфазной электрической цепиВ трёхфазную источник с линейным напряжением Uл = 380 В и частотой f=50 Гц, соединены потребители по схеме «звезда» и «треугольник» (рис.4). Выполнить:
Параметры потребителей соединённых по схеме «звезда»
Параметры потребителей соединённых по схеме «треугольник» :
На рис.4 показана схема трёхфазной элетрической цепи. 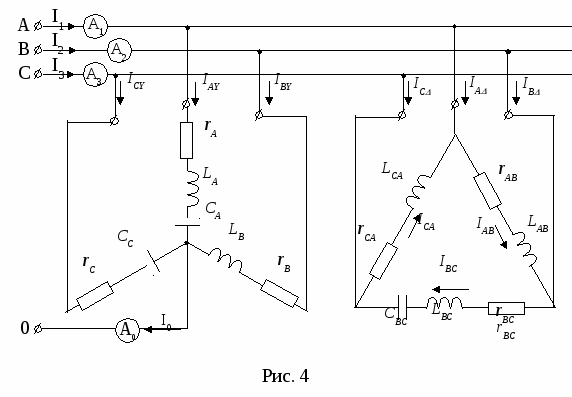 Решение задачи:
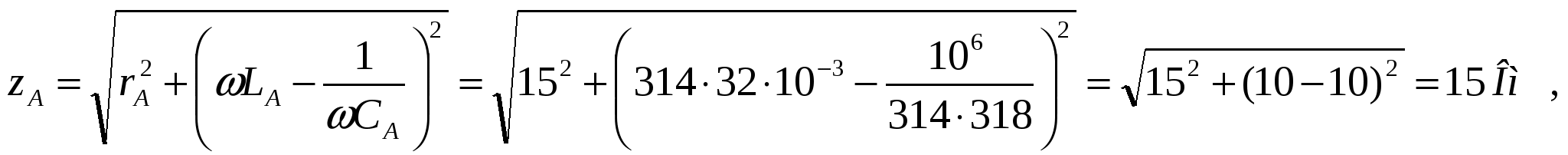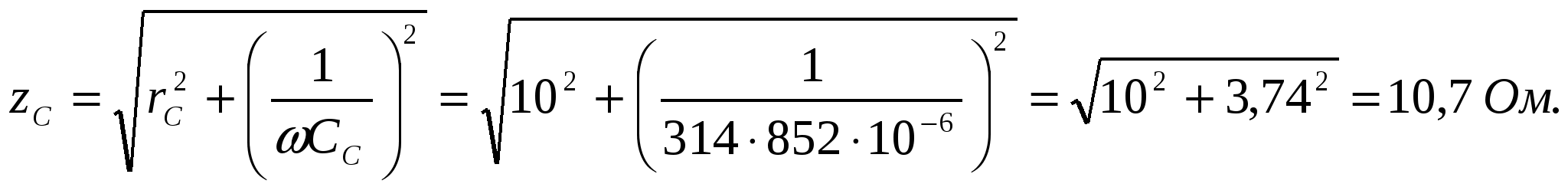      Фазное напряжения при соединение по схеме «звезда» определяется :  Учитовая ,что UA= UB = UC = UФ определяем фазные токи потребителей :   
Для этого определяем полные сопротивления каждой фазы: 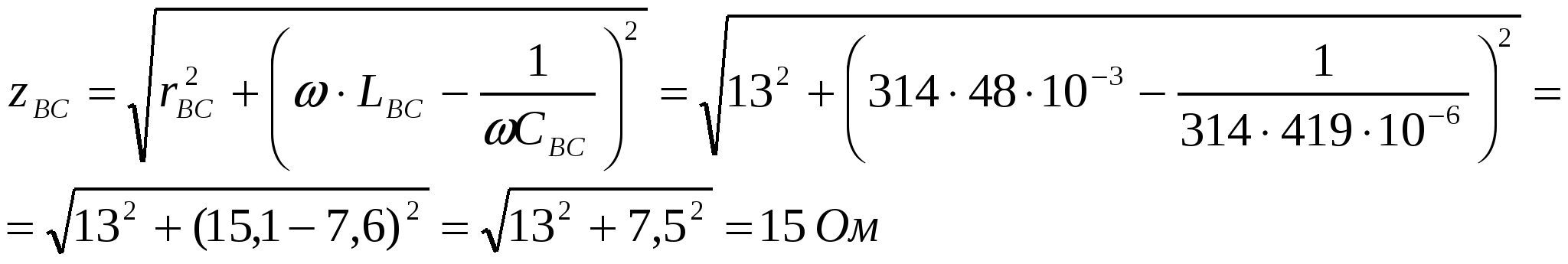   При соединении потребителей по схеме «треугольник» фазные и линейные напряжения равны, т.е. UAB = UBC = UCA = UЛ = 380 В. В этом случае фазные токи:    3. Строим единую векторную диаграмму токов и напряжения для соединения «звезда» и «треугольник», предварительно выбираем масштаб тока и напряжения: а) векторную диаграмму начинаем строить с векторов напряжения и токов потебителей соединённых по схеме «звезда». Для этого выбераем масштаб напряжения mu = 5 B/мм,масштаб тока mi = 1 А/мм .Откладываем вектор фазного напряжения фазы А вертикально (рис 5.). Затем относительно  по направлению часовой стрельки откладываем фазныенапряжения  и  под углом 1200 и 2400. При наличии нулевого провода фазные напяженияUA, UB, UC объразують симметричную систему напряжении.Соеденив концы векторов фазных напряжении получаем треугольник линейных напряжении UAB, UBC ва UCA (рис.5).Для построения векторов фазных токов сначала определим сдвиг фаз между фазными напряжениями. В фазе А потребителя  по этому реактивные напряжения ULA, UCA компенсируются и электрический цепь имеет активный характер. Поэтому Это означает, что фазный ток  и фазное напряжение совпадают по фазе.В фазе В потребитель имеет активно-индуктивный характер,  и ток  отстаёт от вектора напряжения на угол 21030`.В фазе В потребитель имеет активно-ёмкостной характер,  и вектор тока опережает вектор напряжения  на 21030`.Теперь строим вектора фазных токов относительно фазных напряжений потребителя (рис. 5). 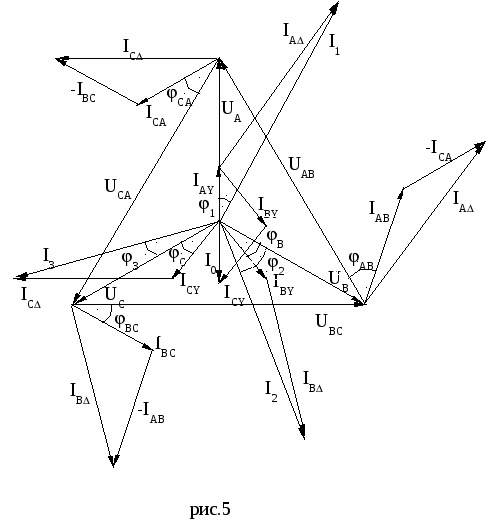 б) аналогично определяются сдвиги фаз между фазными токами IAB, IBC и ICA и фазными напряжениями UAB, UBC и UCA, для потребителей соединённых по схеме «треугольник». Потребитель в фазе АВ имеет активно-индуктивный характер, т.е.  и вектор тока  отстаёт от вектора напряжения на 450 .Потребитель в фазе ВС имеет активно-индуктивный характер, т.е.  т.е. 15,1>7,6. Поэтому  и ток  отстаёт от вектора напряжения  на 29030`.Потребитель в фазе СА также имеет активно-индуктивный характер, т.е. т.е. 15,1>7,6. Поэтому  и ток  отстаёт от вектора напряжения  на 29030`.В векторной диаграмме вектора токов  , ,  строится относительно векторов фазных напряжении  ,  и  (рис.5).4. Из векторной диаграммы (рис.5) определяем ток в нулевом проводе I0 и для схемы треугольник линейные токи   и  :а) ток в нулевом I0 проводе в соответствии I закона Кирхгофа равен геометрической сумме фазных токов:  Для определения действительного значения тока длину вектора  умножаем на масштаб тока т.е.  б) линейные токи потребителей соединённых по схеме “треугольник” 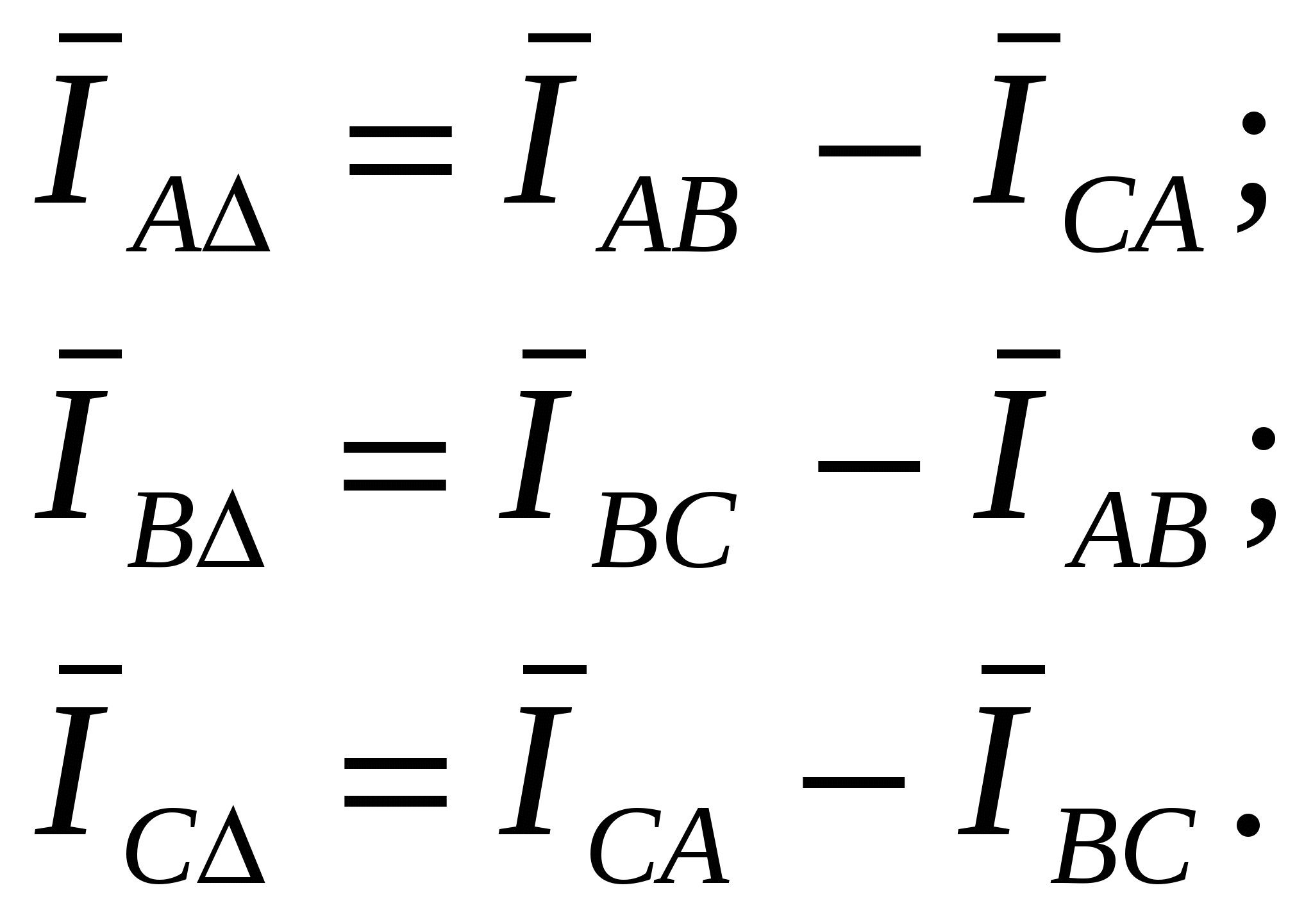 и  определьяется по первому закону Кирхгофа (5-рис): Действительные значения токов и с учётом принятого масштаба для токов (1мм=1А); т.е.    5. Из векторной диаграммы (рис.5) определяют показания амперметров А1, А2 и А3 т.е. величины токов I1, I2 и I3 . Для этого геометрическим суммированием векторов фазных токов IAY, IBY ва ICY и линейных токов IA, IB ва IC определяем показание амперметров А1, А2 и А3 т.е. величины токов I1, I2 и I3: 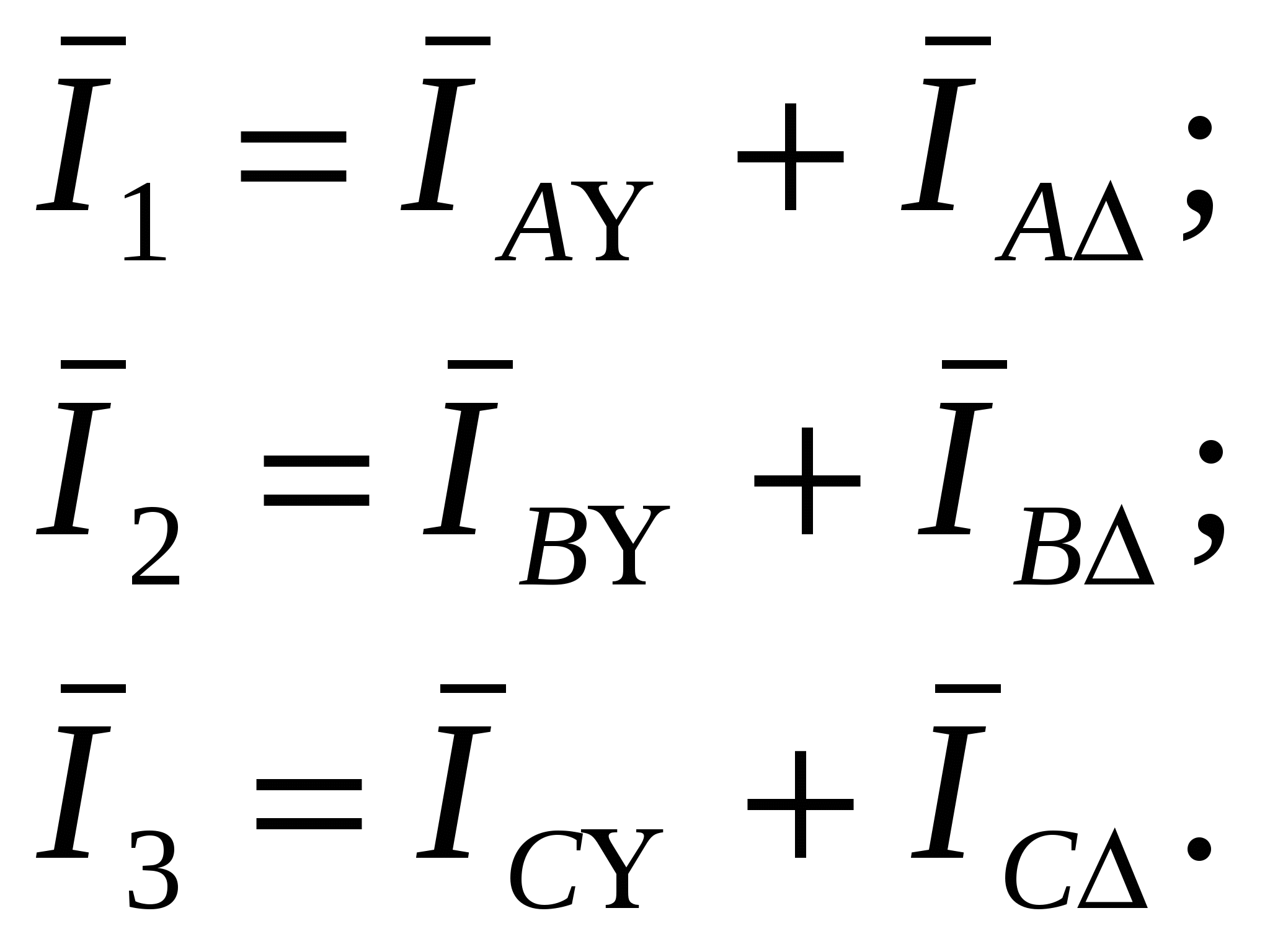 Действительные значения токов 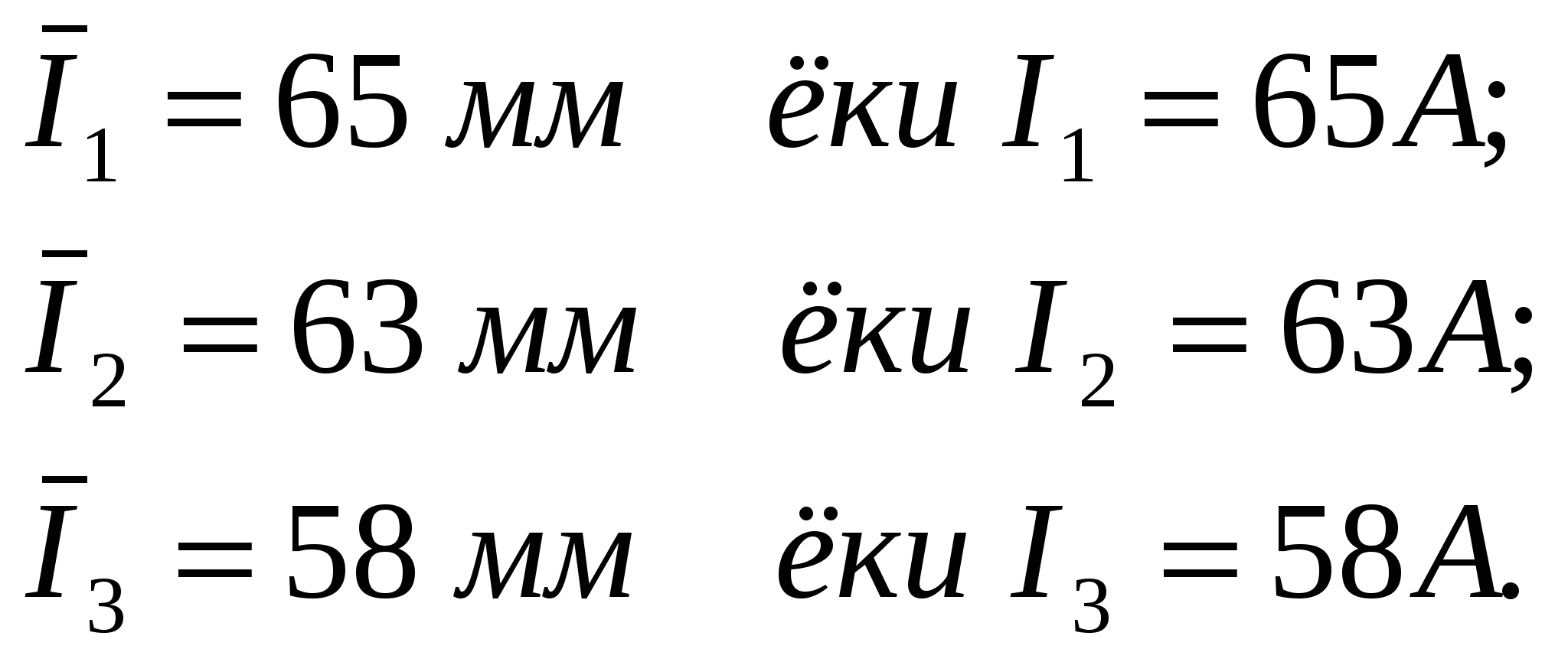  и  с учётом принятого масштаба для токов будет равень:
Активная мощность каждой фазы:    Активная мощность трёх фаз:  Реактивная мощность каждой фазы :    Реактивная мощность трёх фаз:  Полная мощность каждой фазы:    Полная мощность трёх фаз :  б) Активная, реактивная и полная мощность потребителей соединённых по схеме «треугольник» Активная мощность каждой фазы :    Активная мощность трёх фаз:  Реактивная мощность каждой фазы :    Реактивная мощность трёх фаз:  Полная мощность каждой фазы:    Полная мощность трёх фаз :  7. Определение графическим методом активной, реактивной и полной мощностей трёхфазной цепи по данным полученных из векторной диаграммы (рис. 5). Для этого измерим углы 1, 2 ва 3 из векторной диаграммы.  Определяем косинусы этих углов  Определяем синусы этих углов  Активная мощность каждой линии :    Сумарный активный мощность потребителей :  Реактивная мощность каждой линии:    Сумарная активная мощность потребителей:  Полная мощность каждой линии:    Сумарная полная мощность потребителей:  8.Сопоставим мощности полученные аналитическим и графическим методами. Для этого определим полную мощность потребляемую приёмниками:    Варианты для расчёта трёхфазных цепей приведены в таблицах 6,7,8. |
трёхфазного потребителей соединённых по схеме «звезда»; 
и линейные токи 
соединённый по схеме «треугольник»;