Методические указания к выполнению курсовой работы для студентов всех форм обучения

• Название: Методические указания к выполнению курсовой работы для студентов всех форм обучения
• Дата: 12.05.2018
• Размер: 416.78 Kb.
• Имя файла: Dostiarov_A_M__PiGT_Kur_proekt_Metodicheskie_ukazania_k_vypolnen.docx
• Тип: Методические указания; #43413
• страница: 2 из 8

2.4 Расчет регулирующей ступени

 

В курсовой работе для всех вариантов предполагается применение двухвенечной регулирующей ступени (колесо Кертиса). Применение двухвенечной регулирующей ступени позволит:

  сократить число ступеней давления, поскольку колесо Кертиса срабатывает до 1/3 от общего теплового перепада;

 резко снизить давление и температуру пара. Это вызовет рост удельного объема пара за регулирующей ступенью, что увеличит высоту лопаток ступеней давления и ликвидирует на них парциальность. Снижение давления за соплом регулирующей ступени уменьшит утечки пара через переднее концевое уплотнение, а уменьшение температуры пара повысит прочность материала ротора и статора турбины;

 повысить КПД турбины на переменных режимах работы, поскольку колесо Кертиса имеет более пологую характеристику внутреннего относительного КПД (), чем одновенечная регулирующая ступень. Последнее особенно важно для турбин с противодавлением, работающих в режимах резко-переменной нагрузки.

 

2.4.1 Порядок расчета регулирующей ступени

 

1. Задаемся средним диаметром регулирующей ступениd_рс, взяв значение его из прототипа (см. Приложение А).

2. Задаемся отношением X^рс_о =   в пределах X^рс_о = 0,26 ÷ 0,32.

3. Определяем окружную скорость U  на среднем диаметре ступени

                                     , м/с.                                           (2.10)

4. Находим фиктивную скорость С₀ на выходе пара из сопел ступени

                                     , м/с.                                                 (2.11)

5. Вычисляем располагаемый тепловой перепад h^рс_о ступени

                                     , кДж/кг.                                        (2.12)

Контроль:  < (1/3 * H_о).

При ≥ (1/3 * H_о) необходимо увеличить и повторить расчет.

 

6.  Выбираем суммарную степень реакции ступени Σρ      

 

	0,26	0,28	0,30	0,32
Σρ	0,08	0,10	0,12	0,14

 

7. Определяем располагаемый тепловой перепад на сопловую решетку

                                     h_ос = (1- Σρ) , кДж/кг.                              (2.13)

8. Находим по i-s диаграмме состояние пара за сопловой решеткой при изоэнтропийном расширении (точка 3^´    на рисунке 2.1):

а) удельный объем ν ´=  ν_1t , м³/кг;

б) давление , бар.

9. Вычисляем отношение давлений

                                              ε = (2.14)

и сравниваем его с критическим отношением ε_кр = 0,546:

а) при ε < ε_кр необходимо уменьшить d_рс и повторить расчет с п.1 (2.4.1);

б) при ε > ε_кр расчет можно продолжить.

Соблюдение условия ε > ε_кр позволит применить суживающиеся сопла, которые создают дозвуковые скорости истечения пара и обладают более устойчивым и высоким КПД, чем расширяющиеся сопла, создающие сверхзвуковые скорости истечения пара и применяющиеся при ε < ε_кр. Однако последние также эффективны при установке специальных профилей.

10. Рассчитаем теоретическую скорость истечения пара С_1t  из сопловой решетки

                                     С_1t= , м/с.                                     (2.15)

11. Определяем комплекс el_c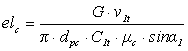

                                     , м                            (2.16)

где e – степень парциальности ступени;

l_c- высота сопла, м;

μ_с = 0,97 – коэффициент расхода сопл;

α₁ - эффективный выходной угол сопл, который выбирается в зависимости от N_э

 

Nэ, МВт	более 100	от 100 до 50	от 50 до 25	от 25 до 10	менее 10
α1,  град	15  16	14	13	12	11

 

При  < 0,002 удовлетворительно спроектировать регулирующую ступень невозможно, и следует, принять меньшее значение d_рс, проделав предыдущий расчет повторно.

 

12. Выбираем оптимальное значение степени парциальности:

	более 0,02	от 0,01 до 0,02	от 0,005 до 0,01
eопт	0,8  0,85	0,5  0,8	0,2  0,5

 

13. Находим высоту сопловой решетки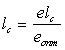

                                      м.                                                    (2.17)

Минимальная высота сопл, которая может быть допущена по условиям потерь в сопловой решетке, l_cmin = 10 * 10^-3 м. Исходя из условий прочности максимальные значения высот сопл - l_cmax = 60 * 10^-3 м

14. Определяем скоростной коэффициент суживающихся сопел φ в зависимости от высоты l_cпо рисунку 2.3.

15. Вычисляем потерю тепла ∆h_c в сопловой решетке

                                     ∆h_c = (1- φ²) h_ос.                                           (2.18)

16. По рисунку 2.4 находим внутренний относительный КПД η_oi^pcступени.

17. Рассчитываем использованный теплоперепад h_i^pcв регулирующей ступени

                                     h_i^pc= η_oi^pc *·h_о^рс, кДж/кг.                                         (2.19)

18. Вычисляем величину энтальпии пара за сопловой решеткой

                                     i₃ = i_o  - h_oc + ∆h_c, кДж/кг.                             (2.20)

19. Находим величину энтальпии пара за регулирующей ступенью

                                       i₄ = i_o - h_i^pc, кДж/кг.                                    (2.21)

20.  Заканчиваем построение предварительной схемы теплового процесса турбины в i-s диаграмме. Определяем давление пара за регулирующей ступенью, для чего необходимо вниз от точки 2 по изоэнтропе S₂ отложить величину располагаемого теплового перепада ступени h_о^рс (точка 4^ на рисунке 2.1). На пересечении линий i₃ = const и изобары Р₁^рс строим точку 3, которая характеризует собой действительное состояние пара за соплами регулирующей ступени. На пересечении линий i₄ = const и изобары
Р₂^рс получаем точку 4 конца процесса в регулирующей ступени и начала процесса в первой ступени давления. Наносим на схему числовые значения всех найденных величин.

Соединив последовательно прямыми линиями точки 1, 2, 3, 4, 5, 6 и 7 получим изображение предварительной схемы теплового процесса турбины в i-s диаграмме.

 

2.5. Расчет первой ступени давления

 

1. Задаемся средним диаметром первой ступени давления d₁ взяв величину его из прототипа.

2. Выбираем величину отношения  

 

Nэ, МВт	более 100	от 100 до 50	от 50 до 25	от 25 до 10	менее 10
Хо	0,5	0,49	0,48	0,46	0,45

 

3. Определяем величину располагаемого теплового перепада h_o¹ на ступень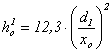

                                     , кДж/кг.                                 (2.22)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 2.3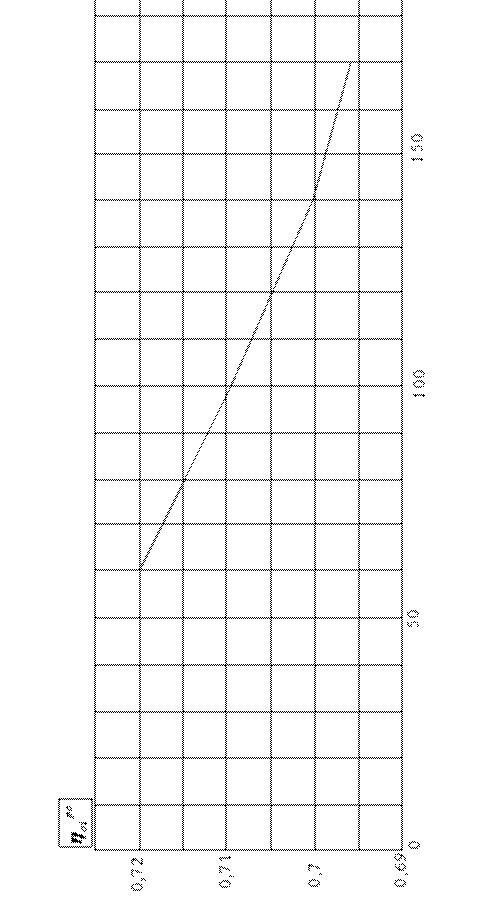

 



Рисунок 2.4

4. Задаемся степенью реакции ρ на среднем диаметре ступени

 

Nэ, МВт	более 100	от 100 до 50	от 50 до 25	от 25 до 10	менее 10
ρ	0,12	0,10	0,08	0,06	0,04

 

5. Находим величину располагаемого теплового перепада сопловой решетки

                                     , кДж/кг.                                 (2.23)

6. Вычисляем теоретическую скорость истечения пара С_1t¹ из сопла

                                     , м/с.                                                   (2.24)

7. По i-s диаграмме определяем удельный объем пара за соплом при изоэнтропийном расширении ν_1t¹. Для этого из точки 4 вниз по изоэнтропе
S₄ откладываем величину h_oc¹. Точка 9 (см. рисунок 2.1) определяет состояние пара за соплом при изоэнтропном расширении.

8. Вычисляем высоту сопловой лопатки ступени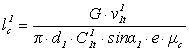

                                     , м                            (2.25)

где μ_с = 0,97 – коэффициент расхода сопла;

α₁ – эффективный выходной угол сопл, который выбирается в зависимости от N_э (см. п. 11 § 2.4.1).

е – степень парциальности.

Для ступеней давления нужно стремиться выполнять подвод пара по всей дуге сопловой решетки, т.е. принимать е=1. Если же окажется, что при выбранном диаметре ступени d₁ и е=1 высота сопла l_c¹будет меньше
(15  20) * 10 ^-3 м, то необходимо либо задаться новым, меньшим значением ступени d₁¹и повторить расчет, либо ввести степень парциальности е<1. Однако введение степени парциальности в ступени давления резко снижает ее КПД, поэтому данным способом пользоваться нежелательно.

9. Определяем длину рабочей лопатки

                                     l_p¹=l_c¹+∆_к+∆_п, м                                            (2.26)

где ∆_к – перекрыша по корневому диаметру, м;

∆ _п – перекрыша по периферийному диаметру, м, (см. рисунок 3.10).

 

Величины перекрыш выбираются в зависимости от l_c.

 

Высота сопловой лопатки lc, 10-3 м.	Величина перекрыши, 10-3 м.
	∆к	∆п
15  35	1,0	2,0  2,5
35  70	1,0	2,0  3,0
70  100	1,5  2,0	2,5  3,5
100  150	1,5  2,0	3,0  3,5
150  300	1,5  2,0	3,0  4,0

 

10. Находим корневой диаметр диска d_к

                                     d_к = d₁ - l_p¹,  м.                                              (2.27)

11. Вычисляем величину, обратную веерности θ₁

                                               .                                                 (2.28)