Устройство СВЧ антенн. Устройства СВЧ и антенны. Методические указания к выполнению курсовой работы для студентов направления
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
2 ОСНОВНЫЕ ТИПЫ АНТЕНН И ИХ ХАРАКТЕРИСТИКИ2.1 Зеркальные антенныВ настоящее время широко применяются зеркальные антенны, как наиболее технологичные и недорогие из всех антенн СВЧ. Простота конструкции, малая масса, хорошие электрические характеристики – вот основные причины широкого использования зеркальных антенн в дециметровом, сантиметровом и миллиметровом диапазонах волн. Параболическая зеркальная антенна одна из наиболее часто применяемых антенн. Теория и вопросы проектирования параболических зеркальных антенн достаточно полно описаны в [1, 7, 11]. В качестве облучателя параболического зеркала часто используют прямоугольный волновод с волной типа Н10. Часто применяют прямоугольный или круглый волновод, нагруженный на рупор. Широко используют облучатель двухщелевого типа, а также вибраторный облучатель. Антенная система со щелевым облучателем оказывается очень компактной. Облучатель создает малое затемнение зеркала. Примером облучателя с круглой поляризацией является спиральная антенна. В качестве облучателя может также использоваться антенна волновой канал и микрополосковая антенна. С развитием техники СВЧ усилителей, обладающих чрезвычайно низким уровнем шумов, оказалось, что антенна дает значительный вклад в общую шумовую температуру системы. Шумовую составляющую можно уменьшить путем тщательного проектирования антенны. 2.1.1 Основные геометрические соотношения и расчет направленных свойств зеркальных антеннЧаще всего рефлектор является симметричной или несимметричной поверхностью вырезанной из параболоида вращения (рис. 5), который в прямоугольной системе координат (x, y, z) описывается уравнением: а в сферической (r, ψ, α) с началом в фокусе параболоида: 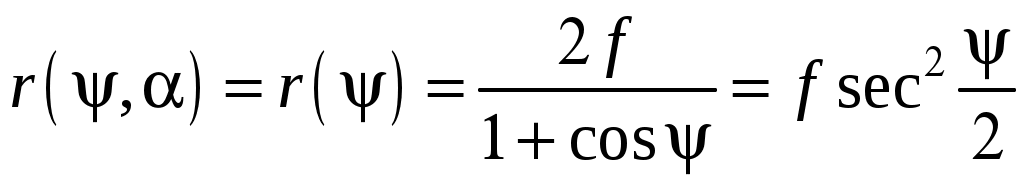 . (29) . (29)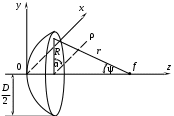 Рис. 5. Параболическая зеркальная антенна Радиус раскрыва R, угол раскрыва ψ0 и фокусное расстояние f связаны соотношениями:  . (30) . (30)В большинстве практических случаев 45° < ψ0 < 90°, так что 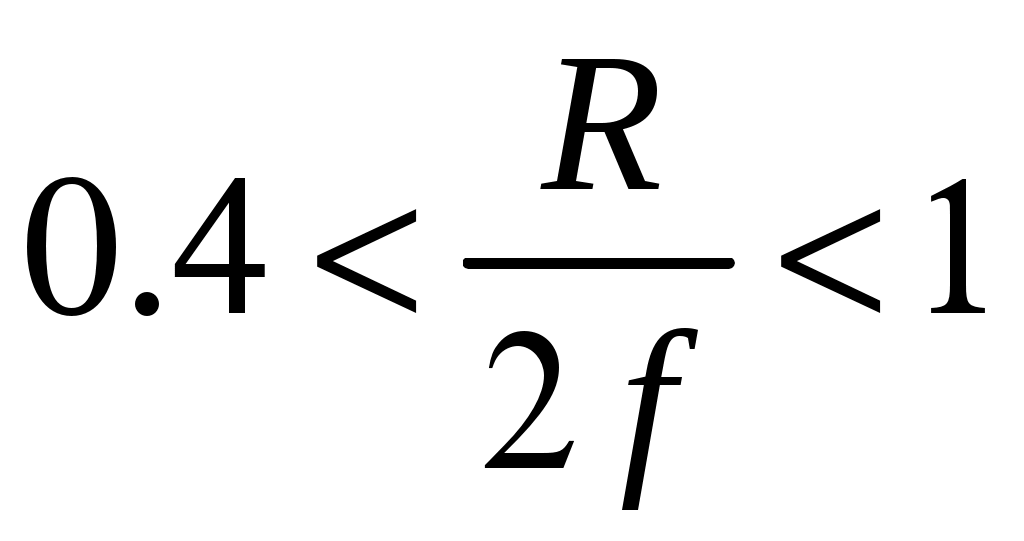 . .Из (30) легко определить глубину зеркала: 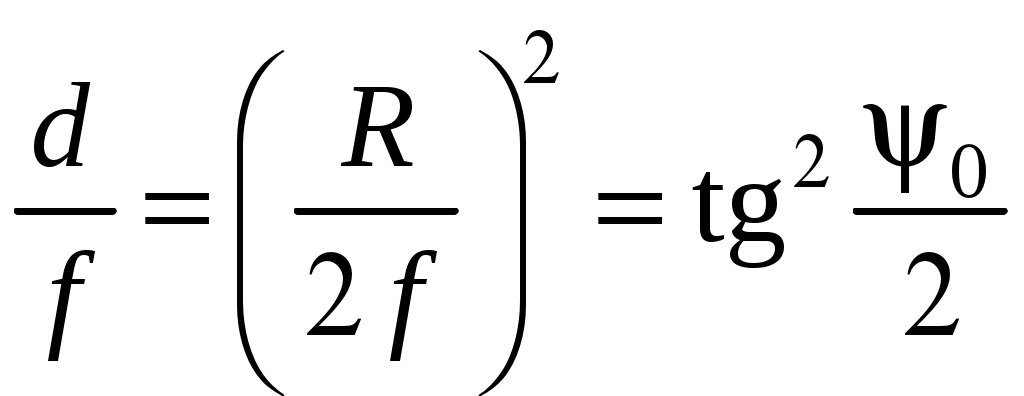 . (31) . (31)Наиболее просто направленные свойства параболической антенны рассчитываются так называемым апертурным методом, т. е. по полю в ее апертуре, представляющей собой минимальную плоскую поверхность, закрывающую антенну. При установке в фокусе параболического рефлектора облучателя с диаграммой направленности Fобл(ψ, α) в апертуре зеркала наводится синфазное поле с амплитудным распределением: 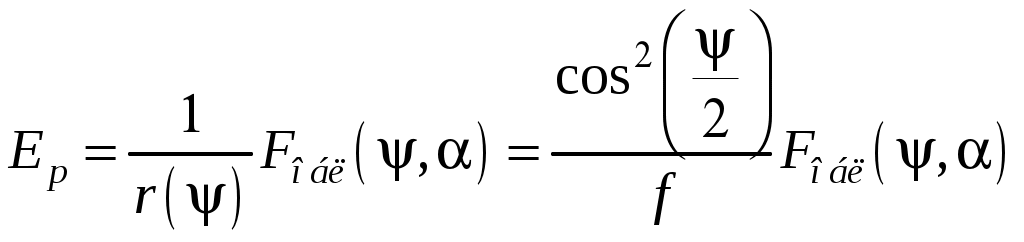 . (32) . (32)При этом координаты точек раскрыва xр, yр, или ρр, αр связаны с углами ψ и α соотношениями, обусловленными геометрией задачи.  (33) (33)По известному полю в апертуре зеркала рассчитывается диаграмма направленности антенны F(θ, φ):  , (34) , (34)где Коэффициент направленного действия антенны с учетом апертурного коэффициента использования γa, обусловленного амплитудной неравномерностью поля в раскрыве, и коэффициента перехвата мощности облучателя зеркала γп рассчитывается по формуле: 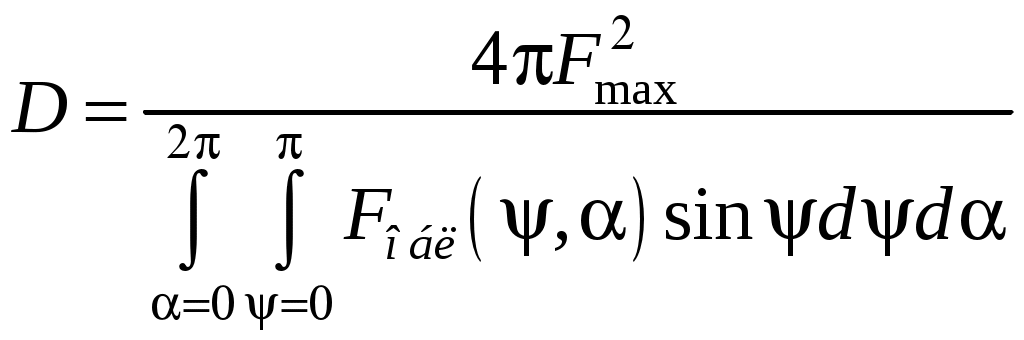 , (35) , (35)где 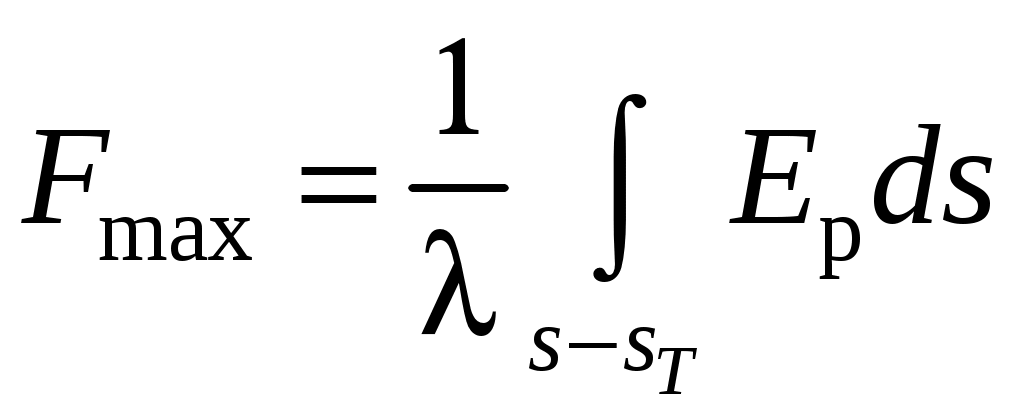 . .Общая эффективность антенны γ = γа γп определяется из соотношения:  . (36) . (36)Ширина диаграммы направленности синфазного раскрыва в общем случае обратно пропорциональна размеру раскрыва, выраженному в длинах волн, и также зависит от его формы и распределения поля на нем. В таб. П.6. и П7 приложения Б, приведены основные расчетные соотношения для синфазных раскрывов прямоугольной и круглой формы при некоторых законах распределения поля, допускающих аналитическую оценку интеграла в (35). Как видно из таблиц, чем сильнее спадает поле в раскрыве к его краям, тем при тех же размерах антенны больше ширина главного лепестка и ниже уровень боковых лепестков. Необходимо отметить, что затенение раскрыва зеркала облучателем или другими элементами антенны может значительно повысить уровень боковых лепестков по сравнению с незатененным раскрывом. В качестве облучателей параболических рефлекторов могут использоваться простые слабонаправленные излучатели: рупорные, вибраторные, спиральные, щелевые, полосковые. Форма диаграммы направленности облучателя должна соответствовать форме раскрыва зеркала. Необходимый спад интенсивности облучения к краям зеркала определяется двумя факторами: общей эффективностью антенны и уровнем боковых лепестков (УБЛ). Если УБЛ не задан, то при проектировании антенны следует добиваться максимальной эффективности. Можно показать, что при этом облучение краев зеркала должно быть на 9-11 дБ ниже, чем облучение центра, а эффективность составляет 70-80%. Если же требуется низкий УБЛ, то уровень облучения краев может быть ниже 9-11 дБ, что приводит также к снижению общей эффективности антенны. 2.2 Волноводные излучатели и рупорные антенныВолноводные излучатели и рупорные антенны являются одним из распространенных типов антенн СВЧ и используются не только как самостоятельные антенны, но и как первичные излучатели других, более сложных антенн этого диапазона частот (зеркальных, линзовых). Простейшим излучателем сантиметровых волн является открытый конец прямоугольного или круглого волновода (рис. 6). 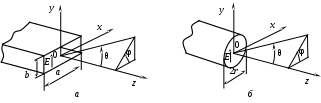 Рис. 6. Антенна в виде открытого конца волновода: а – прямоугольный волновод; б – круглый волновод Так как размеры выходного отверстия волновода невелики (обычно меньше длины волны), то антенны в виде открытого конца волновода – принципиально слабонаправленные антенны. Излучатель в виде открытого конца прямоугольного волновода (рис. 6, а), возбуждаемого волной H10, характеризуют параметры: а) ширина луча на уровне 0.5 по мощности (в радианах) в плоскости H(φ = 0): в плоскости E(φ = π/2): где λ – длина волны, см; а, b– размеры сечения волновода; б) КНД: где ν – КИП раскрыва, равный 0,81. Такими же параметрами характеризуется и излучатель в виде открытого конца круглого волновода (рис. 6, б) при возбуждении его волной H11:  . (42) . (42)Здесь 2r – внутренний диаметр волновода; ν – КИП раскрыва, равный 0.84. 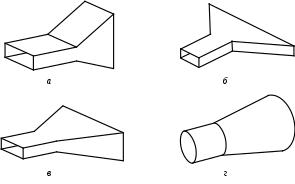 Рис. 7. Рупорные антенны: а – Е секториальный; б – Н секториальный; в – пирамидальный; г – конический Для получения большей направленности волноводный излучатель превращают в рупорную антенну. Наиболее распространены секториальные (рис. 7, а, б), пирамидальный (рис. 7, в) и конический (рис 7, г) рупоры с прямолинейными образующими. Форма главного лепестка амплитудной ДН рупорной антенны зависит от угла раствора рупора. Исследования показали, что при постоянной длине рупора наибольшая направленность излучения для секториальных рупоров получается при углах раствора рупора, которые соответствуют следующим фазовым ошибкам (в радианах) на краях раскрыва: Ф = 3π / 4 в плоскости Н, Ф = π / 2 в плоскости Е. Рупоры с такими значениями максимальных фазовых ошибок получили название оптимальных. Размеры оптимального H - плоскостного секториального рупора (рис. 7, а) связаны между собой соотношением: 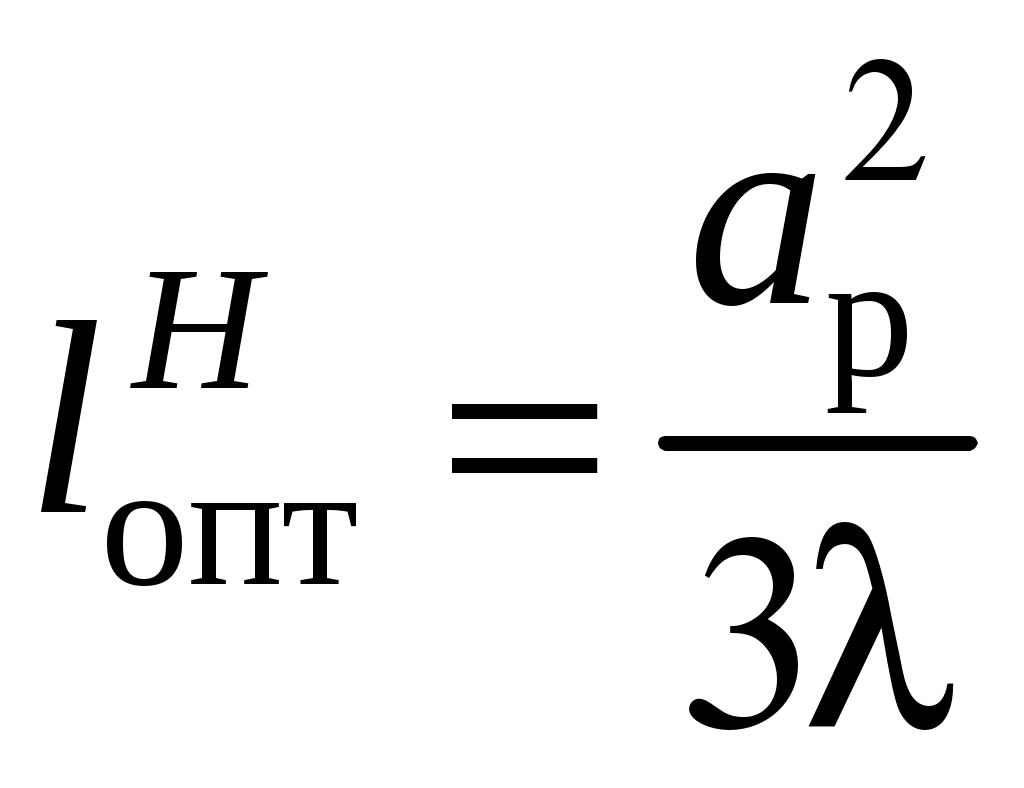 , (43) , (43)где lопт – оптимальная длина и ширина раскрыва рупора. Ширина луча такого рупора на уровне 0.5 по мощности (в радианах) рассчитывается по формулам: в плоскости H: 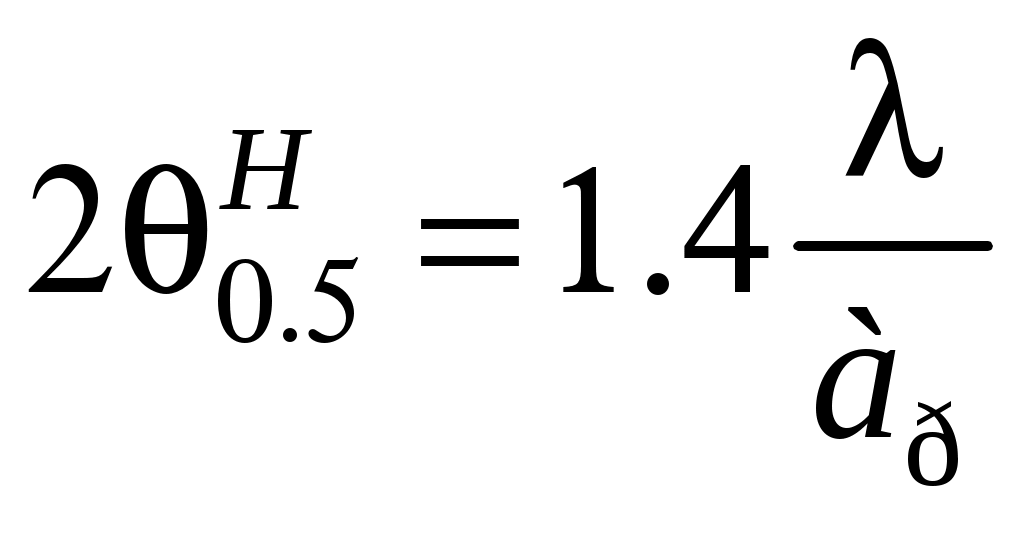 ; (44) ; (44)в плоскости Е: Размеры оптимального E-плоскостного секториального рупора (рис. 7, б) связаны между собой соотношением: 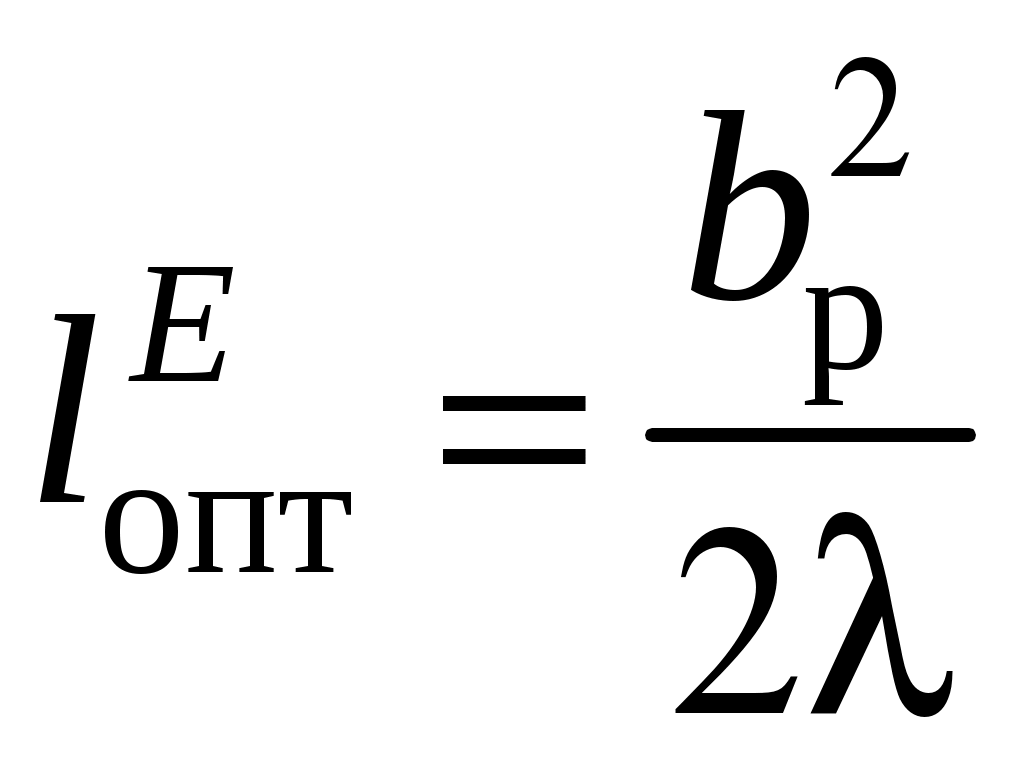 , (46) , (46)где bp – ширина раскрыва рупора. Ширина луча на уровне 0.5 по мощности (в радианах) этого рупора определяется по формулам: в плоскости H: в плоскости E: 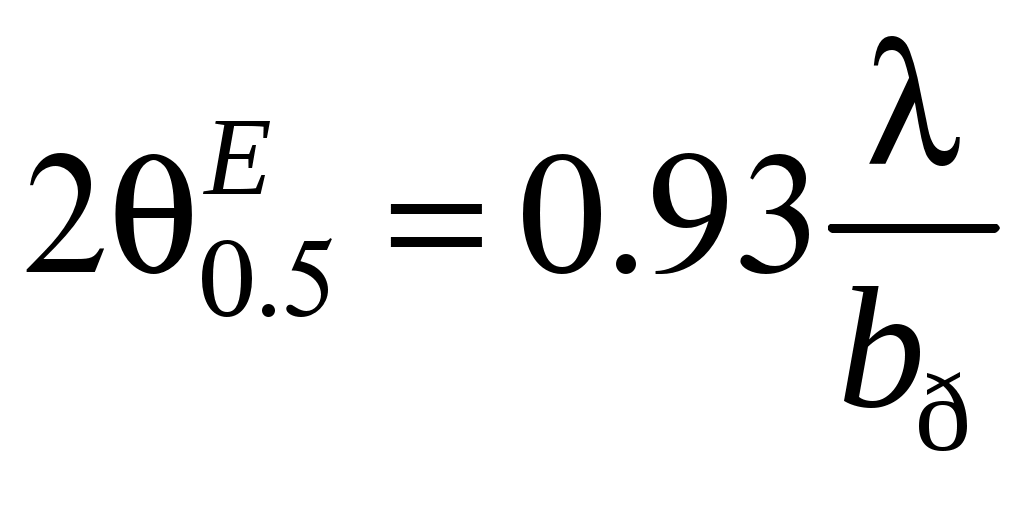 . (48) . (48)КНД оптимальных секториальных рупоров рассчитывается так: 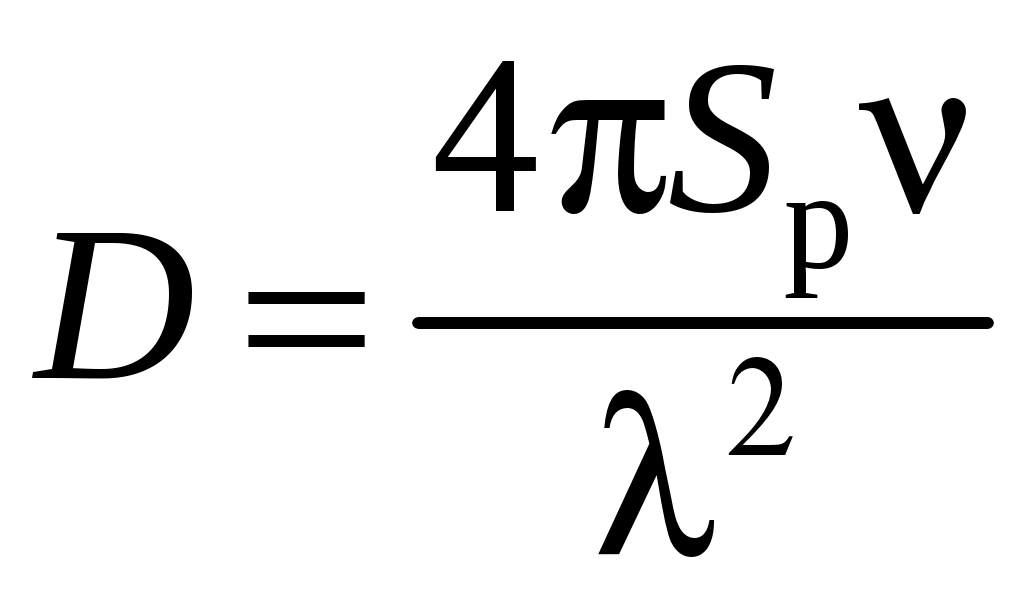 , (49) , (49)где Sр – площадь раскрыва рупора; ν – КИП раскрыва, равный 0.64. Пирамидальный рупор может быть клиновидным (как показано на рис. 7, в) или остроконечным (когда ребра рупора сходятся в одной точке). Нормированные амплитудные ДН пирамидальной рупорной антенны при возбуждении ее волной H10 приближенно можно рассчитать по формулам для прямоугольной синфазной апертуры с косинусоидальным в плоскости H и постоянным в плоскости E амплитудными распределениями: в плоскости H: 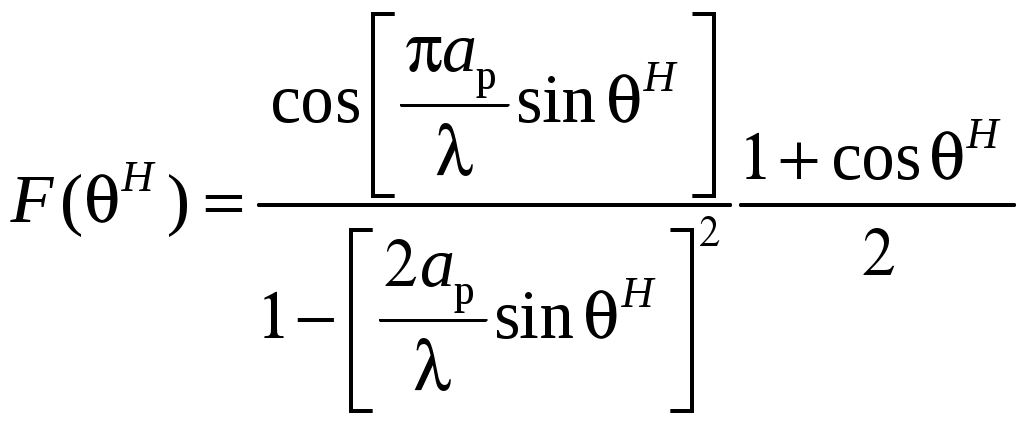 ; (50) ; (50)в плоскости E: 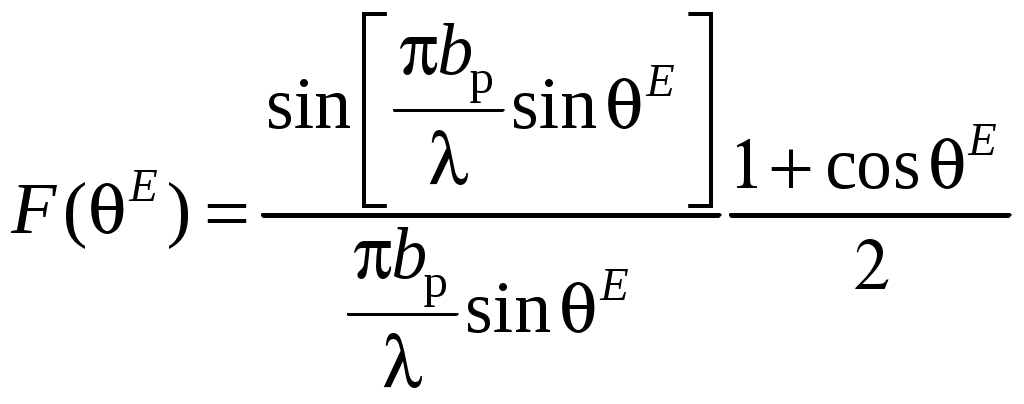 , (51) , (51)где θH и θE – углы, отсчитываемые от оси рупора в плоскостях H и E. Улучшенными характеристиками с точки зрения диапазонности и уровня боковых лепестков амплитудной ДН обладают рупорные антенны со ступенчатыми, криволинейными (в частности, экспоненциальными) и гребенчатыми образующими. Подбором ступенек и формы кривой образующей диапазон рабочих частот таких антенн может быть расширен в 1,5–2 раза, а пространственная амплитудная ДН приближена к осесимметричной. Коэффициент усиления рупорных антенн практически равен КНД: поскольку потери в таких антеннах обычно малы. 2.3 Проволочные антенныК так называемым «проволочным» антеннам можно отнести все типы штыревых антенн, антенны типа «волновой канал», петлевые антенны. Проволочные антенны представляют собой конструкции, состоящие из отрезков прямолинейных проводов, определенным образом расположенных в пространстве. Современные проволочные антенны широко используются как в виде самостоятельных элементов (одиночные вибраторы), так и в составе антенных решеток. В волноводных, рупорных, зеркальных и других антеннах их используют в качестве возбудителей. Основной задачей теории излучения является определение электромагнитного поля излучения антенн. Принципиально эта задача может быть решена путем применения уравнений Максвелла с учетом граничных условий на поверхности антенны. Антенна в общем случае рассматривается как проводящее, полупроводящее или непроводящее тело определенной конфигурации, возбуждаемое заданной системой источников и расположенное в свободном пространстве или вблизи других тел. При этом учитываются реальные свойства среды и граничные условия, необходимые для получения однозначного результата решений уравнений Максвелла. Решение задачи о распределении тока в антенне в строгой постановке обычно сопряжено с математическими трудностями. Однако к настоящему времени получен ряд новых положительных результатов и роль строгой теории антенн неуклонно растет благодаря появлению возможностей решения сложных задач с помощью ЭВМ. При решении задачи о прямолинейном тонком электрическом вибраторе в строгой постановке функция распределения тока по вибратору считается неизвестной, а проекции векторов электрического поля выражаются через эту функцию. Из условия равенства нулю касательной к поверхности вибратора составляющей напряженности электрического поля составляют интегральное уравнение относительно искомой функции тока вибратора. Решая это уравнение, находят функцию распределения тока по вибратору, а затем и все необходимые вторичные параметры [18]. Такой способ расчета антенн называется методом интегрального уравнения. В результате решения основной задачи теории излучения определяют параметры антенны как излучающего устройства: входное сопротивление, коэффициент бегущей волны, относительную полосу пропускания, добротность, коэффициент полезного действия, диаграмму направленности, коэффициенты направленного действия, усиления, эллиптичности поляризационной характеристики, действующую длину антенны и др. Первые три из перечисленных параметров характеризуют антенну как нагрузку для генератора (приемника) переменных токов высокой частоты, а остальные в большей степени − как излучатель (приемник) электромагнитной энергии. Эти параметры необходимы при изготовлении, настройке и эксплуатации вибраторных антенн. Данные антенны широко используются в радиосвязи, в том числе и подвижной, в радиовещании и телевидении, а также радиолокации. Теория и вопросы проектирования проволочных антенн различного назначения достаточно полно описаны в [1, 4, 14, 15, 18, 19]. При расчете рекомендуется использовать программы MMANA, NEC-2 for MMANA [14, 15], Mininec classic и др. При этом в отчете приводятся входной файл и результаты расчетов. 2.3.1 Симметричный вибраторСимметричный вибратор является одной из наиболее широко распространенных простых антенн, применяемых главным образом в диапазонах коротких и ультракоротких (метровых и дециметровых) волн. Комплексная амплитуда электрического в дальней зоне симметричного вибратора в предположении синусоидального закона распределения тока I вдоль вибратора (рис. 8) для воздушной среды определяется по формуле: где Ia, – амплитуда тока в точках питания вибратора; r – расстояние от вибратора до точки наблюдения; k = 2/ – волновое число, в котором – длина волны; l – длина плеча вибратора; F() – нормированная амплитудная ДН вибратора в плоскости, проходящей через ось вибратора (плоскость Е), причем: 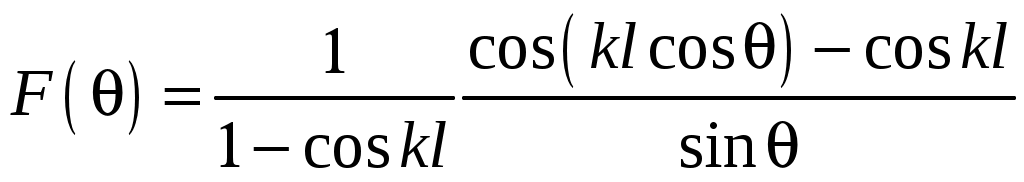 . (54) . (54)в выражении (54) – угол между осью вибратора и направлением в точку наблюдения (рис. 8). Выражением (53) можно пользоваться при длине вибратора 2l < 5/4. Если 2l > 5/4, то необходимо определить направление максимального излучения, затем вычислить нормирующий множитель. 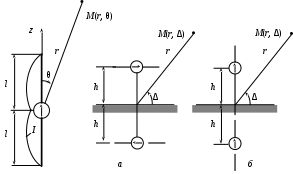 Рис. 8 Симметричный вибратор Рис. 9 Вибратор над землей Для наиболее распространенного на практике полуволнового вибратора (2l = /2) имеем: 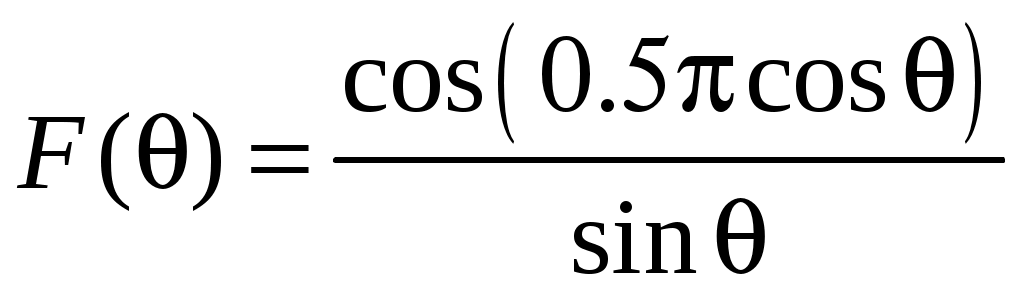 . (55) . (55)В плоскости, перпендикулярной к оси (плоскость Н), симметричный вибратор любой длины свойством направленности излучения не обладает и его амплитудная ДН в этой плоскости имеет вид окружности, поскольку F() = 1. При расположении вибратора над землей, которую принято считать идеально проводящей, результирующая амплитудная ДН с учетом влияния земли находится по правилу перемножения диаграмм: Fрез = FуFз, где Fу – нормированная амплитудная ДН уединенного вибратора; Fз – множитель, которым учитывается влияние земли. При этом горизонтальный вибратор, размещенный на высоте hнад поверхностью земли (рис. 9, а), и его зеркальное изображение образуют систему двух противофазных излучателей, расположенных на расстоянии 2h друг от друга, так что пространственная характеристика направленности системы принимает вид: 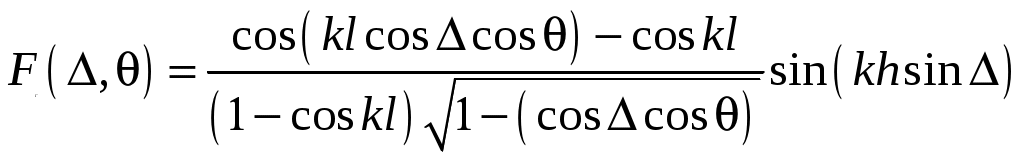 , (56) , (56)где – угол возвышения (между поверхностью земли и направлением в точку наблюдения), а – угол, отсчитываемый от оси вибратора в горизонтальной плоскости. При определении амплитудной ДН поднятого над землей вертикального вибратора (рис. 9, б) последний вместе с его зеркальным изображением образует систему двух синфазных излучателей, расположенных на расстоянии 2h друг от друга, и пространственная характеристика направленности в этом случае будет: 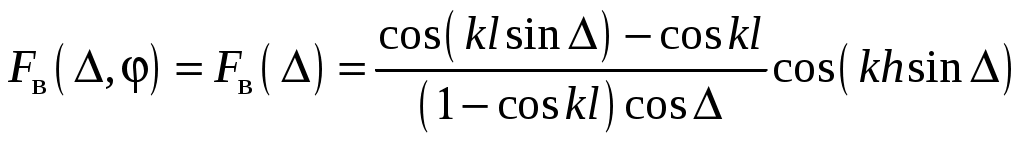 , (57) , (57)так как Fв() = 1. Действующая длина (в метрах) симметричного вибратора при l /2определяется по формуле: 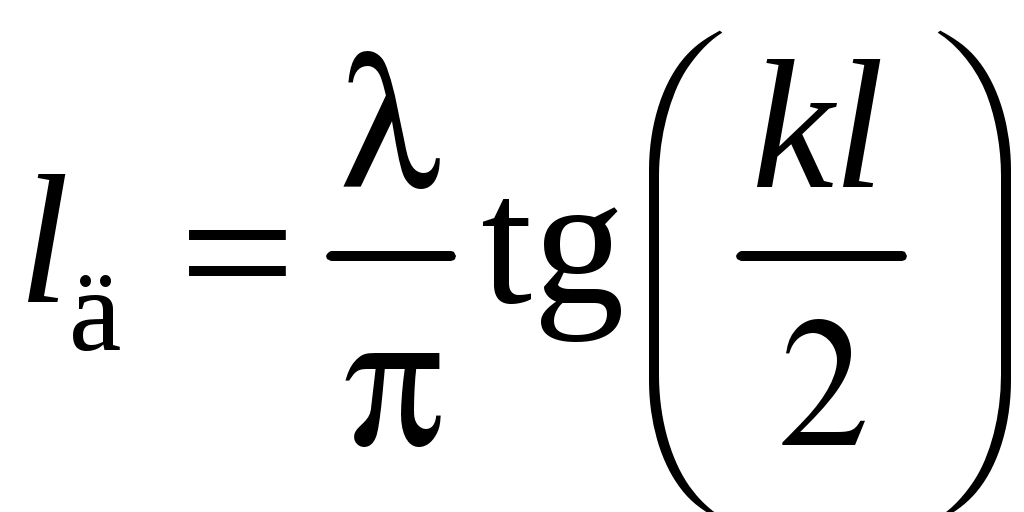 . (58) . (58)Для полуволнового вибратора (2l = /2) действующая длина равна: Зная действующую длину вибратора, можно найти его сопротивление излучения, связывающее мощность излучения с квадратом действующего значения тока. При длине вибратора 2l /2сопротивление излучения (в Омах) определяется по формуле: 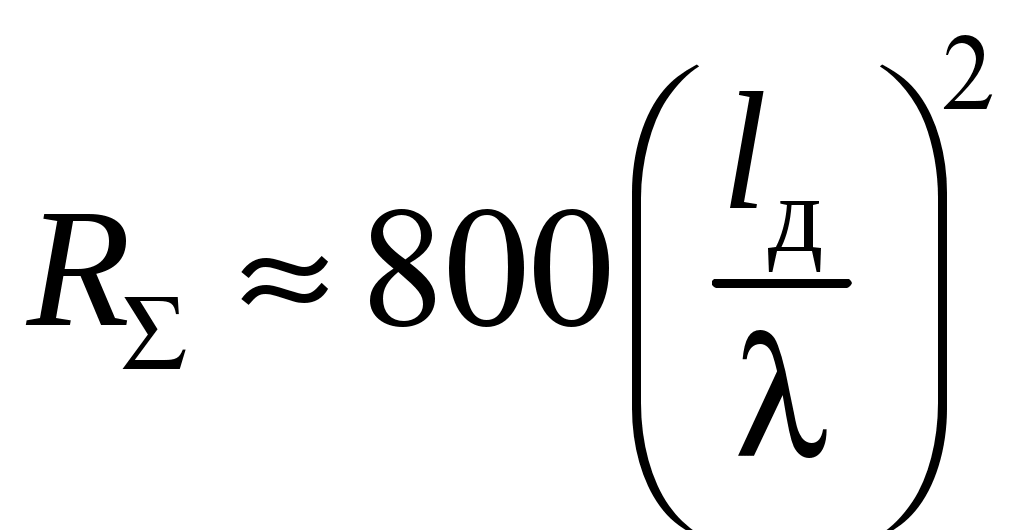 . (60) . (60)Сопротивление излучения может быть отнесено к току в точках питания вибратора или к току в пучности. Выше оно было приведено к току в точках питания Iа. Сопротивление излучения, отнесенное к пучности тока Iп: где R – сопротивление в точках питания симметричного вибратора. При небольших тепловых потерях электромагнитной энергии в проводе вибратора, что чаще всего имеет место на практике, входное сопротивление симметричного вибратора (в Омах) может быть вычислено по приближенной формуле: 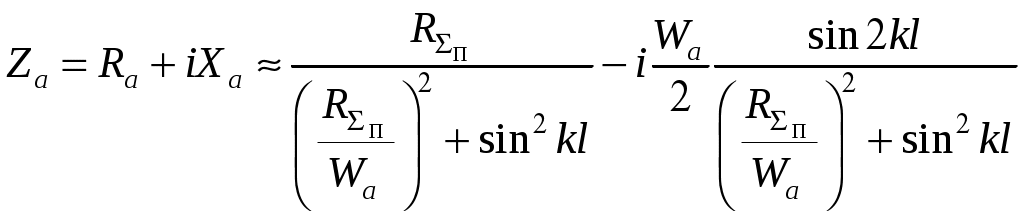 , (62) , (62)где Wa – волновое сопротивление вибратора, обычно рассчитываемое (в Омах) по формуле Кессениха: 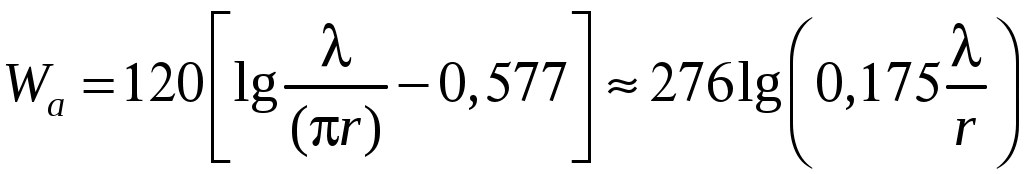 . (63) . (63)Здесь r – радиус провода вибратора. Резонансное укорочение плеча симметричного вибратора рассчитывается по формуле:  , (64) , (64)где – коэффициент укорочения волны в вибраторе. В случае полуволнового вибратора укорочение плеча: 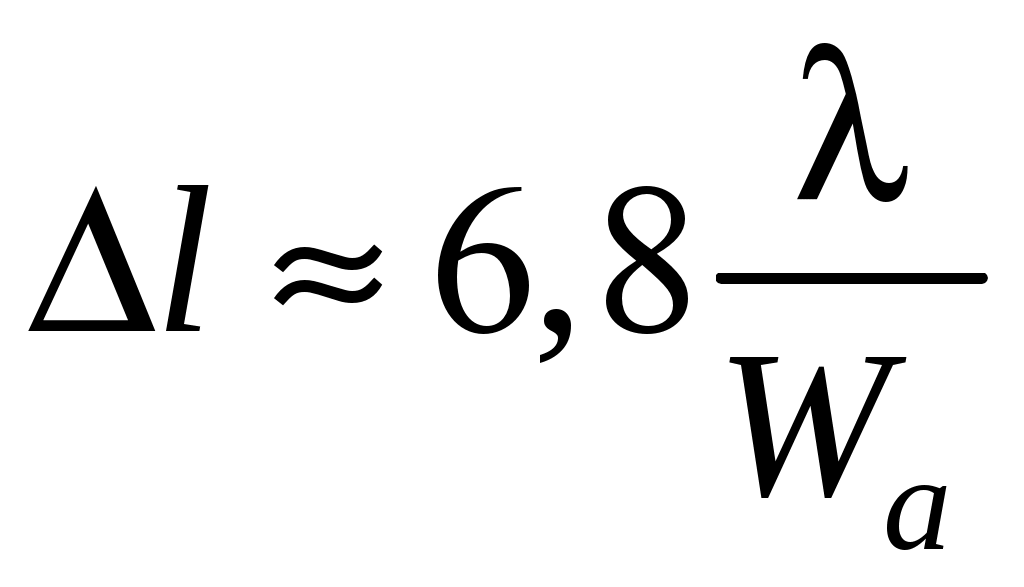 . (65) . (65)Относительная ширина полосы рабочих частот (в процентах) такого вибратора: 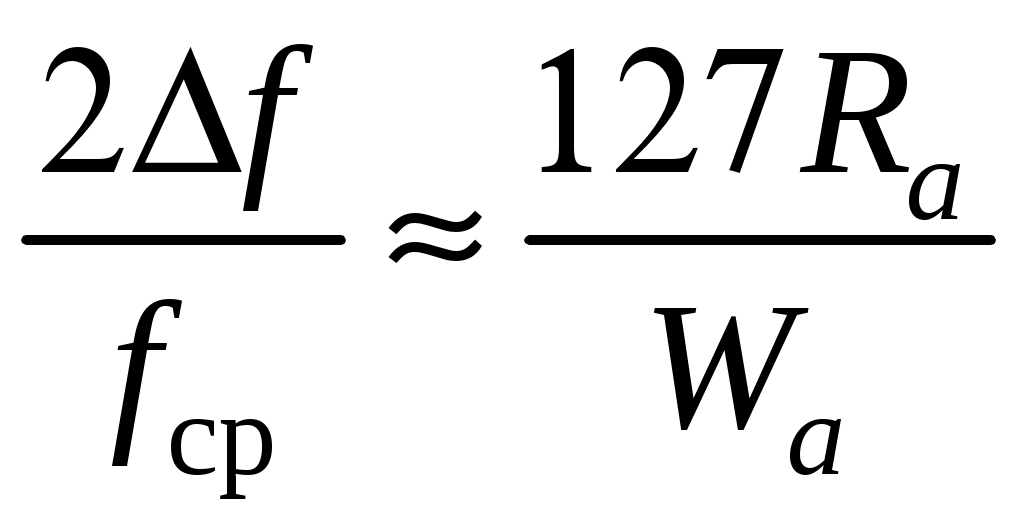 . (66) . (66)КНД симметричного вибратора рассчитывается по формуле: 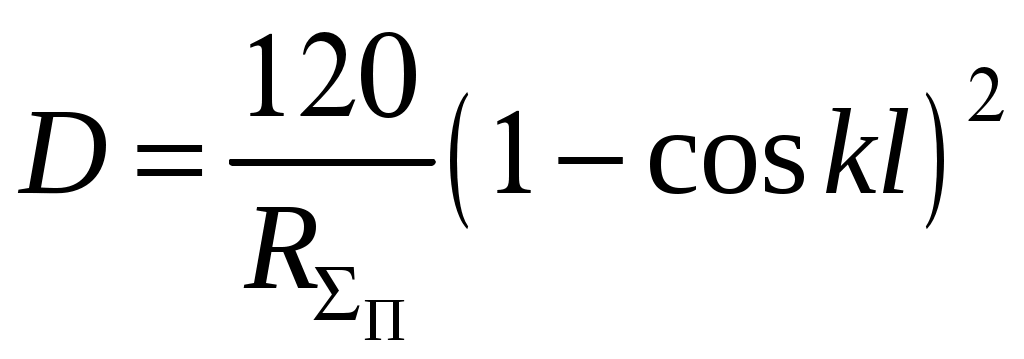 . (67) . (67)2.3.2 Директорные антенныДиректорная антенна, или антенна типа «волновой канал», образуется из проволочных вибраторов, расположенных параллельно в одной плоскости (рис. 10). Вибратор 1 (обычно полуволновой) соединяется с фидером и является первичным излучателем антенны. Все остальные вибраторы с фидером не связываются и являются вторичными излучателями, причем те из них, которые расположены в направлении максимального излучателя антенны (на рис. 10 это вибраторы 2), имеют длину 2lд < λ/2 и называются директорами, а вибратор 3, находящийся по другую сторону от вибратора 1 и имеющий длину 2lp > λ/2 – рефлектором. Широкое применение такие антенны получили на метровых и дециметровых волнах: в телевидении и радиовещании, на радиорелейных линиях небольшой протяженности, радиолокации и так далее. 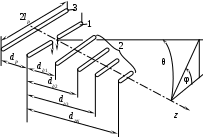 Рис. 10. Антенна «волновой канал» Вибраторы 2 и 3 антенны возбуждаются за счет взаимных связей между ними и вибратором 1. Размеры и расположение директора должны быть подобраны так, чтобы вдоль антенны распространялась замедленная поверхностная волна, и обеспечивался режим осевого излучения. Токи во всех вибраторах директорной антенны находятся из системы уравнений Кирхгофа:  , (68) , (68)гдеIр,Iизл, Iдn – комплексные амплитуды токов в рефлекторе, излучателе и в одном из директоров соответственно; Zр.р, Zи.и, Zд.д – собственные сопротивления рефлектора, излучателя и одного из директоров соответственно; Zр.и, ZрдN – взаимные сопротивления рефлектора и излучателя или директора соответственно; bи.дN – взаимные сопротивления излучателя и одного из директоров; Zдmдn – взаимные сопротивления т-гои n-го директоров; Uизл – напряжение на зажимах излучателя. После того как из системы уравнений найдены токи во всех вибраторах при заданной геометрии директорной антенны, можно рассчитать ее амплитудные ДН по формулам: в плоскости Н(φ = π/2) 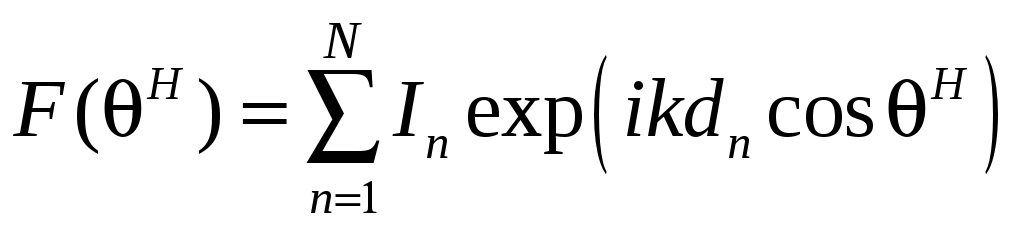 ; (69) ; (69)в плоскостиE(φ = 0) 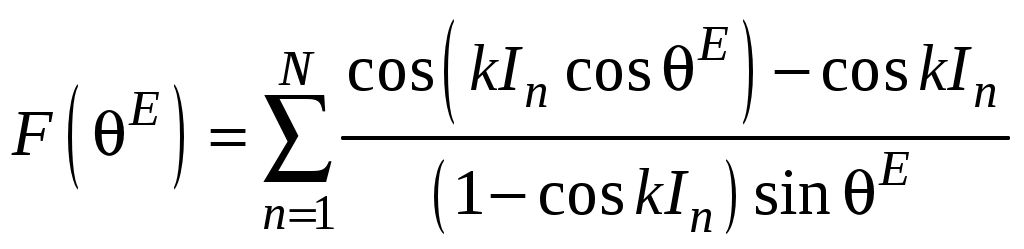 . (70) . (70)Здесь θ – угол между осью антенны и направлением в точку наблюдения; N – полное число вибраторов в антенне; k = 2π/λ – волновое число, в котором λ – длина волны. В формулах (69) и (70) все вибраторы пронумерованы с помощью индекса п, причем п = 1, 2, 3, ..., N. Рефлектору соответствует n = 1, первичному излучателю – n = 2 и так далее. Начало системы координат находится в центре первичного излучателя и d1 = – dp. Для приближенной оценки характеристик директорной антенны можно считать, что dn = ndср, 2ln = λ/2, In = I0exp[–i(n – 1)ψ], ψ = π/2. в плоскости Н(φ = π/2): 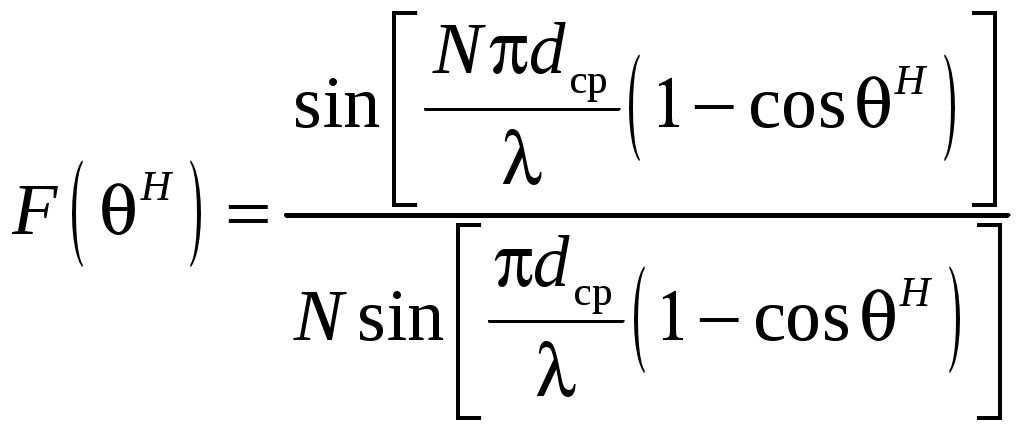 ; (71) ; (71)в плоскости E(φ = 0): 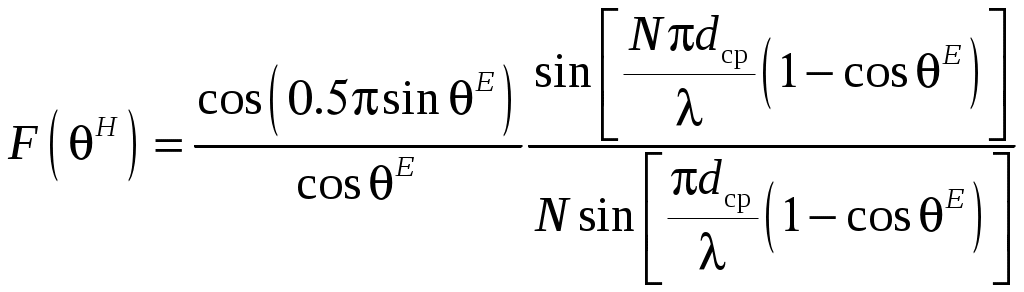 . (72) . (72)Ширина луча антенны на уровне 0.5 по мощности в плоскости Е (в радианах) определяется по формуле: а в плоскости H – по формуле: КНД и эффективная площадь директорной антенны рассчитываются по формулам: 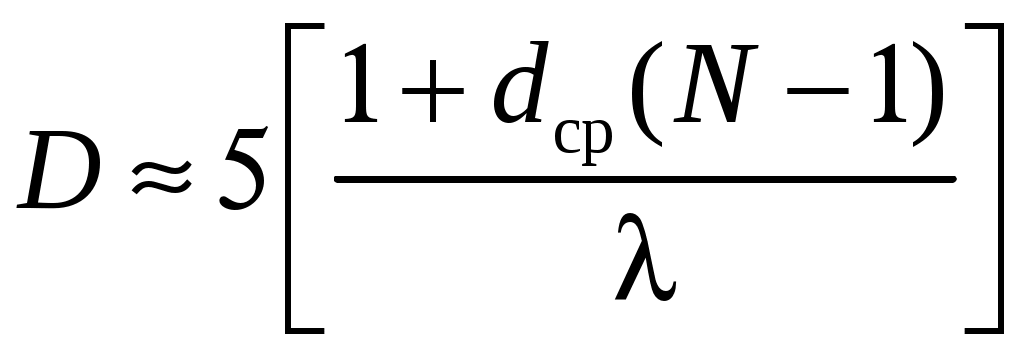 , (75) , (75)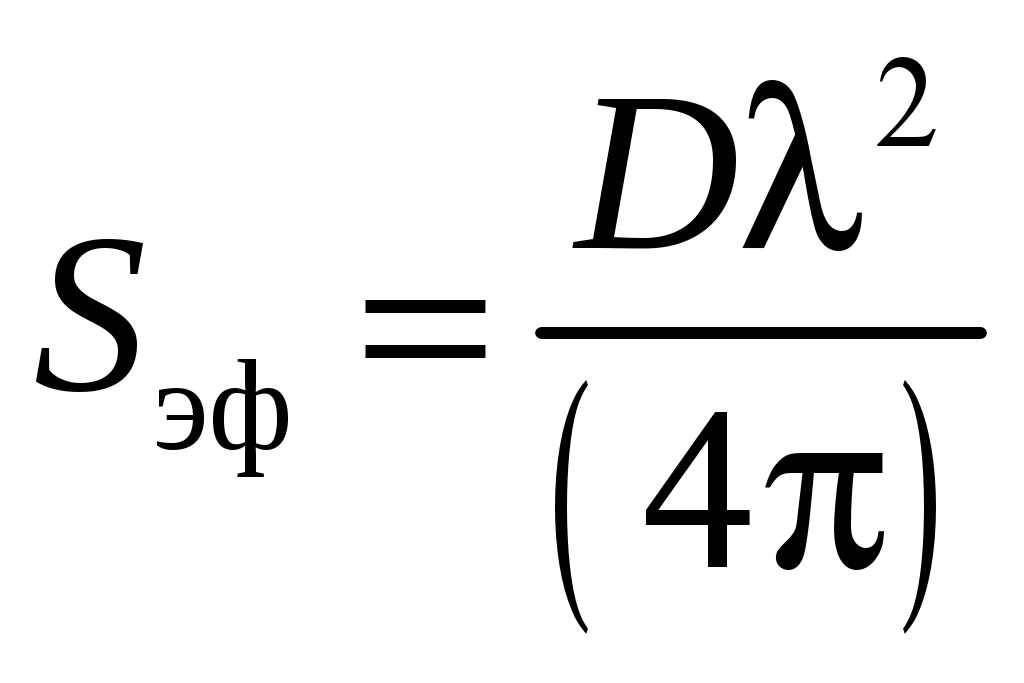 . (76) . (76)Точный расчет геометрии директорной антенны по заданным характеристикам приводит к задаче ее конструктивного синтеза. В качестве целевой функции задают максимум КНД или приближение к заданной ДН. В процессе решения находят длины всех вибраторов 2ln и все расстояния dn. 2.3.3 Спиральные антенныСпиральные антенны относятся к типу антенн, электромагнитное поле излучения которых имеет вращающуюся (круговую) поляризацию в направлении оси антенны. Такие антенны широко используются в радиолокации для получения более контрастного изображения цели на фоне помех, а также при работе с летательными и космическими аппаратами, положение антенн которых изменяется в пространстве во времени. Спираль может работать как самостоятельная антенна или являться элементом антенной решетки либо облучателем зеркальной антенны. Наиболее часто применяются цилиндрическая и каническая спиральные антенны с односторонним излучением (рис. 11), получаемым с помощью плоского сплошного или сетчатого металлического экрана, помещаемого перед спиралью и выполняющего роль рефлектора. 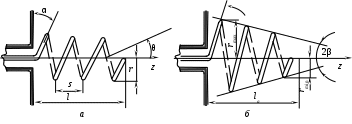 Рис. 11 Спиральные антенны: а – цилиндрическая спираль; б – коническая спираль Геометрическими параметрами цилиндрической спирали (рис. 11, а) являются: lа – осевая длина; l – длина одного витка; s – расстояние между соседними витками (шаг спирали; r – радиус намотки; N – число витков и α - угол подъема витка (шаговый угол). Между этими параметрами существует связь: У конической спирали (рис. 11, б) длина витка и расстояние между витками переменны, ее параметрами являются: lа – осевая длина; rmin – минимальный радиус намотки; rmaх – максимальный радиус намотки; N – число витков; α – угол подъема витка и β – половина угла при вершине конуса. Геометрические размеры конической спирали определяются по формулам: 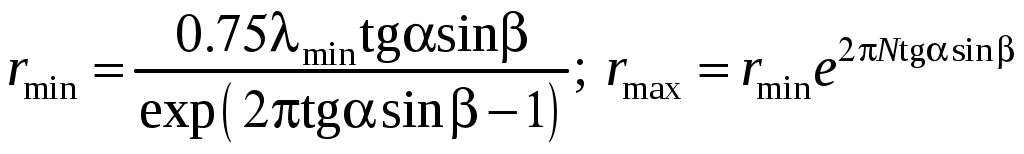 , (78) , (78)где λmin – нижняя длина волны рабочего диапазона антенны. В режиме осевого излучения вдоль оси цилиндрической спиральной антенны распространяется замедленная волна. Это происходит при условии, если вдоль одного витка спирали укладывается одна длина волны λ, то есть Чтобы получить максимальный КНД антенны, надо взять длину спиральной антенны, равную:  , (80) , (80)где ξ = 1 ÷ 1.4 – коэффициент укорочения волны, бегущей вдоль антенны. При этом ДН антенны рассматривается по формуле: 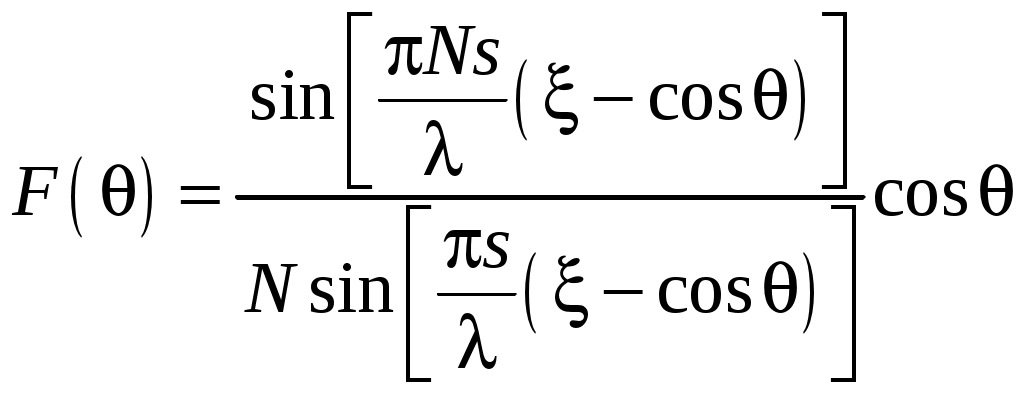 , (81) , (81)где θ – угол между осью антенны и направлением в точку наблюдения. В режиме осевого излучения при оптимальном значении ξ и N > 3 цилиндрическую спиральную антенну характеризуют параметры: а) ширина луча на уровне 0.5 по мощности (в радианах)  , (82) , (82)на уровне нулевого излучения (в радианах): 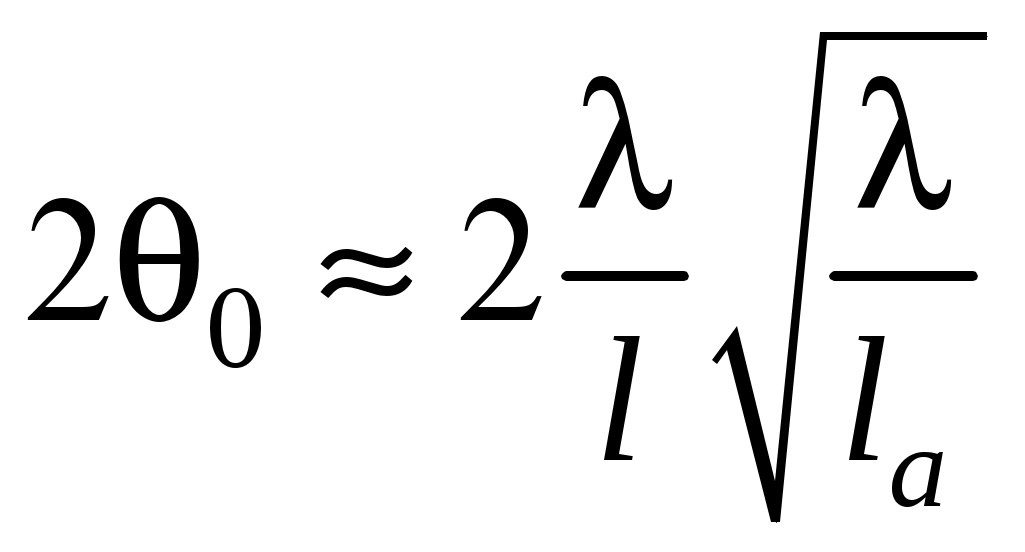 ; (83) ; (83)б) КНД: 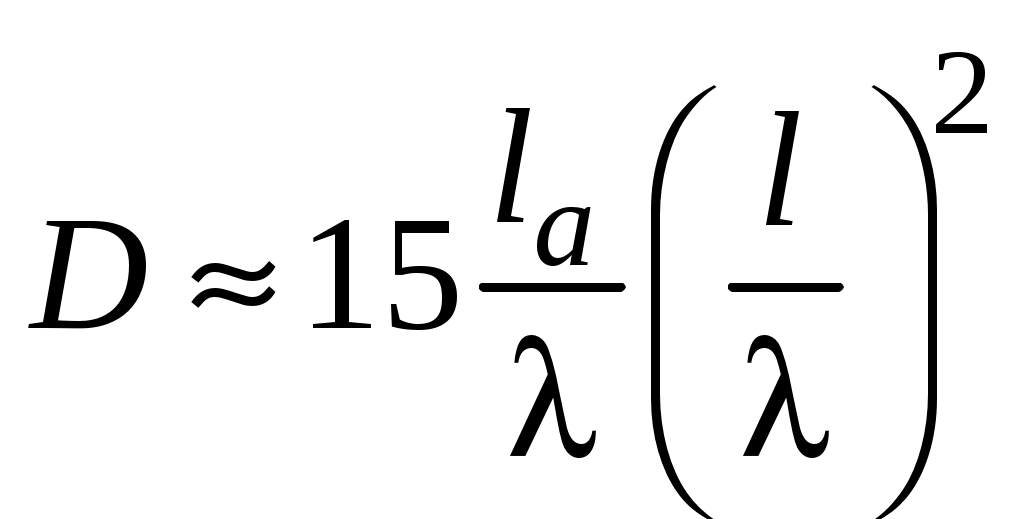 ; (84) ; (84)в) входное сопротивление (в Омах) : При настройке цилиндрической спиральной антенны на максимальный КНД в направлении ее оси будет не круговая, а эллиптическая поляризация. Чтобы получить круговую поляризацию, размеры антенны должны удовлетворять соотношению Таким образом, условие получения максимального КНД и условие излучения поля круговой поляризации противоречивы. На практике отдают предпочтение первому или второму условию в зависимости от того, что важнее - направленность спиральной антенны или круговая поляризация ее излучения. Конические спиральные антенны более широкополосны, но имеют меньший КНД из-за уменьшения числа витков, для которых выполняется условие обеспечения режима осевого излучения. 2.4 Антенные решеткиАнтенные решетки (АР) представляют собой комбинацию отдельных излучающих элементов. Параметры АР определяются геометрическим расположением излучающих элементов, а также амплитудой и фазой сигналов возбуждения. В пределах апертуры АР находятся множество одинаковых излучающих элементов, таких, как щели, диполи, волноводы, микрополосковые (печатные) излучатели (в принципе любая антенна, в том числе и зеркальная). В настоящее время отчетливо выявились широкие области использования АР. Такие системы необходимы в остронаправленных антеннах с электрическим сканированием для высокой скорости обзора пространства или многоцелевой работы радиолокационных станций. В радиоастрономии и системах дальней связи решетки из больших зеркальных антенн резко увеличивают КНД. Применение АР в бортовых устройствах позволяет использовать в качестве антенны внешнюю поверхность аппарата. Бурное развитое микроэлектроники в последние годы нашло отражение в антенной технике. Действительно, антенны и устройства СВЧ радиосистем в обычном (не микроэлектронном) исполнении занимают не менее половины всего объема радиотехнической системы и, переход на микроэлектронное исполнение только аппаратуры не приводит к желаемому результату. Микроэлектронное исполнение всей радиосистемы потребовало создание модулей АР, в частности, микрополосковых (печатных) излучающих элементов [8]. Теория и вопросы проектирования антенных решеток различного назначения достаточно полно описаны в [1, 7, 8]. 2.4.1 Волноводно-щелевые антенные решетки (Вщар)Компактность и возможность выполнения щелевых антенн заподлицо с металлической обшивкой делают их чрезвычайно удобными для размещения на летательных аппаратах, особенно на скоростных самолетах и ракетах. На рис. 12, а изображена многощелевая антенна СВЧ, состоящая из полуволновых резонансных щелей, прорезанных в шахматном порядке по обе стороны от средней линии широкой стенки прямоугольного волновода с волной 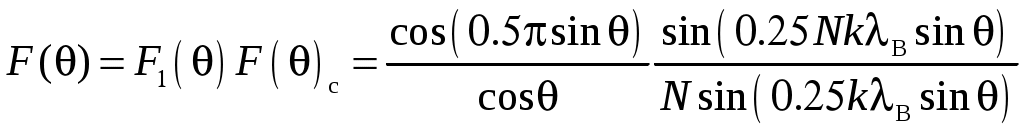 , (87) , (87)где θ – угол между нормалью к широкой стенке волновода и направлением в точку наблюдения; 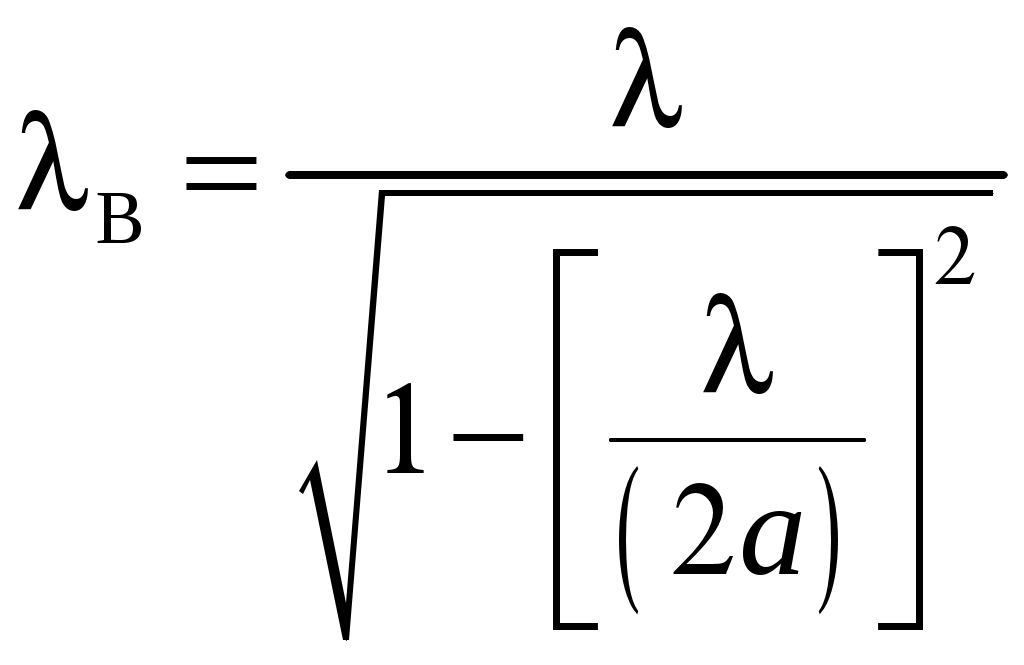 , (88) , (88)в которой а – размер широкой стенки волновода. 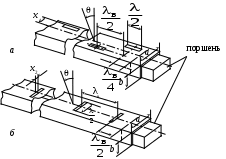 Рис. 12. Варианты расположения щелей в волноводно-щелевой антенной решетке резонансного типа: а – продольные противофазные щели; б - поперечные щели В другом варианте синфазной многощелевой антенны СВЧ с поперечными щелями (рис. 12, б) нормированная амплитудная ДН в продольной плоскости описывается выражением: 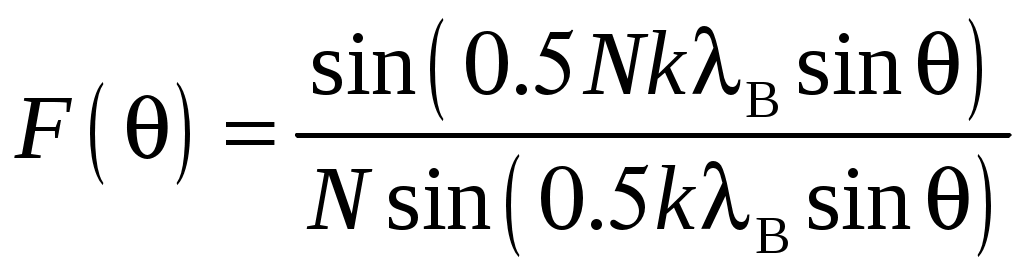 . (89) . (89)Щель, прорезанная в волноводе, нарушает режим бегущих волн внутри волновода и вызывает отражение электромагнитной энергии. На эквивалентной схеме волновода щель можно представить в виде некоторого сопротивления, включенного параллельно или последовательно в зависимости от положения щели. Продольная щель эквивалентна параллельно включенному сопротивлению, поперечная – последовательному. При расчете согласования многощелевых антенн СВЧ обычно пользуются последовательным сопротивлением и параллельной проводимостью. Эквивалентная проводимость продольной полуволновой щели, расположенной на расстоянии x1 от середины широкой стенки волновода с волной H10,рассчитывается по формуле: 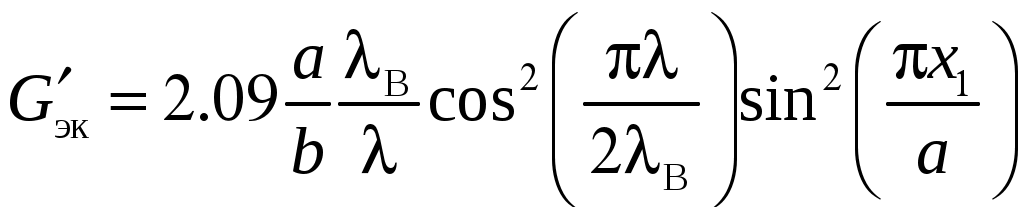 , (90) , (90)где a, b – размеры волновода. Эквивалентное последовательное сопротивление поперечной полуволновой щели,нормированное к волновому сопротивлению волновода с волной 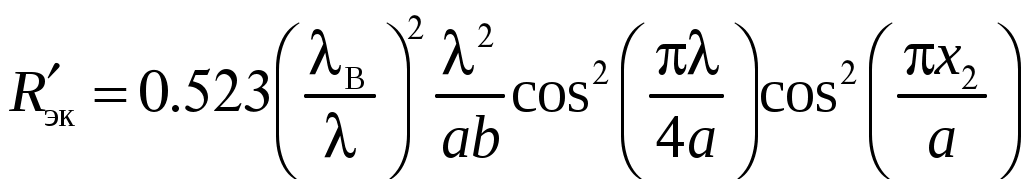 , (91) , (91)где x2 – смещение центра щели относительно середины широкой стенки волновода. Для того чтобы в возбуждающем антенну волноводе установился режим бегущих волн, должно выполняться условие: 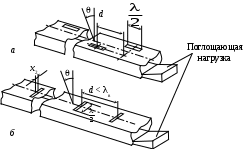 Рис. 13. Варианты расположения щелей в волноводно-щелевой антенной решетке бегущей волны: а – продольные противофазные щели; б - поперечные щели Синфазные волноводно-щелевые антенны – узкополосны. Чтобы расширить диапазон рабочих частот, применяют несинфазные-антенны (рис. 13), соседние щели которых возбуждаются со сдвигом фаз ψ = 2πd/λв (d – расстояние между центрами соседних щелей). При небольшом расфазировании щелей нормированные амплитудные ДН таких антенн рассчитываются по формулам (87), (89), а смещение главного максимума ДН относительно нормали к широкой стенке волновода (в радианах) определяется по формуле: 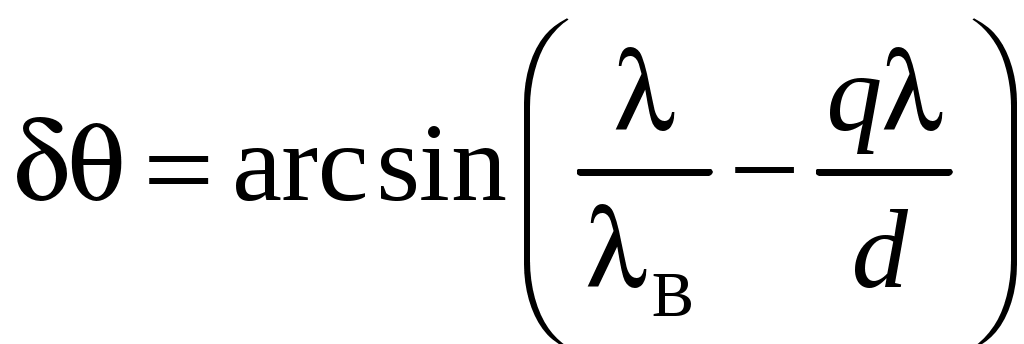 , (93) , (93)где q = 0.5 – для переменнофазно-связанных щелей с возбуждающим волноводом;q = 0 – для синфазно-связанных щелей. |
