Устройство СВЧ антенн. Устройства СВЧ и антенны. Методические указания к выполнению курсовой работы для студентов направления

• Название: Методические указания к выполнению курсовой работы для студентов направления
• Анкор: Устройство СВЧ антенн
• Дата: 10.09.2021
• Размер: 1.25 Mb.
• Имя файла: Устройства СВЧ и антенны.doc
• Тип: Методические указания; #231141
• страница: 3 из 9

3. Полосковые антенны

В ДМ и СМ диапазонах волн находят применение антенны, выполненные по технологии печатных схем. Такие антенны отличаются пониженным весом и габаритами, а также технологичностью изготовления. На рис. 14 приведены эскизы двух разновидностей наиболее употребительных на практике полосковых антенн – прямоугольной и круглой, с возбуждением полосковой и коаксиальной линией. Для согласования точка возбуждения смещена от края антенны (размеры y₀ и ρ₀ на рис. 14).

В режиме основного типа колебаний антенны, изображенные на рис. 14 имеют ДН однолепесткового характера с максимумом, ориентированным в направлении нормали к плоскости диска (θ = 0°).


Рис. 14. Микрополосковый излучатель: а – прямоугольный; б – круглый
Приведем расчетные формулы для прямоугольной антенны. Входное сопротивление в точке резонанса чисто активное и равно: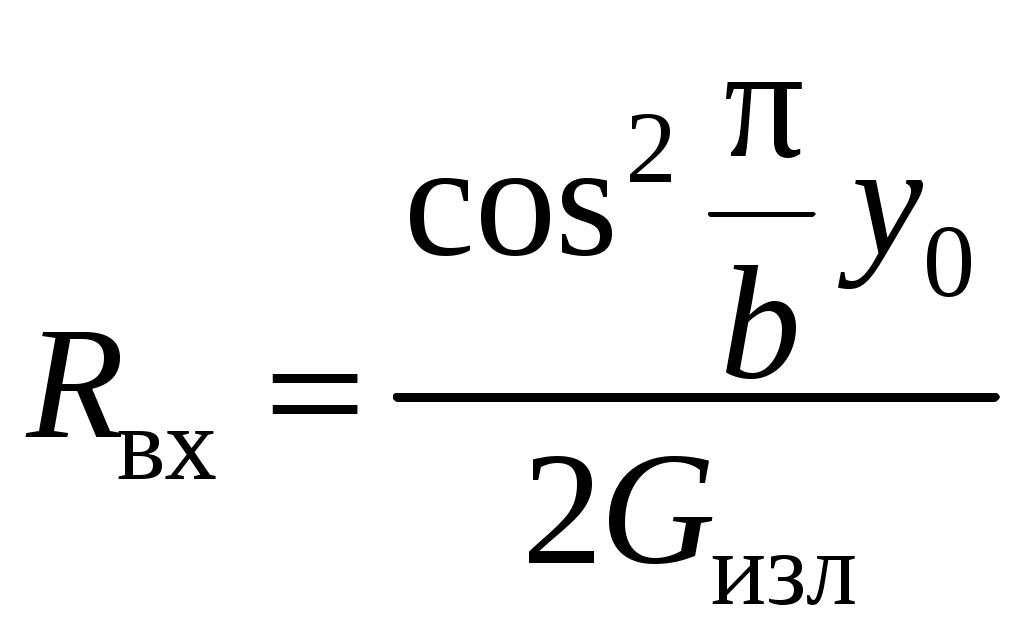
, (95)
где – проводимость излучения торца резонатора:
. (96)
Резонансная длина антенны:
, (97)
– относительная диэлектрическая проницаемость материала положки.

Рекомендуемый размер a от до .

Диаграмма направленности прямоугольной антенны рассчитывают по формуле:
. (98)
Входное сопротивление круговой дисковой антенны (рис. 14, б) в точке резонанса:
, (99)
где J₁(x) – функция Бесселя первого порядка.

Резонансная частота для основного типа колебаний дисковой полосковой антенны определяется формулой:
, (100)
где:
. (101)

Выражение для ДН дисковой антенны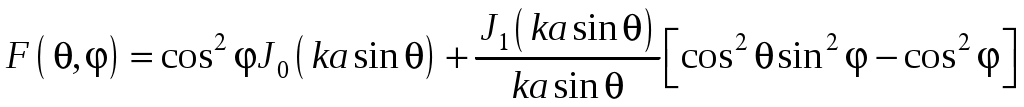
. (102)
Прямоугольная и круглая полосковая антенны, работающие в режиме основного типа колебаний, излучает поле линейной поляризации (вектор E в плоскости Y0Z) c высокой степенью подавления кроссполяризационной составляющей.

4. Фазированные антенные решетки

Антенная решетка (АР) представляет собой группу излучающих элементов, расположенных на некотором расстоянии друг от друга, причем токи в каждом элементе, в общем случае, имеют определенную амплитуду и фазу. Поле решетки определяется путем суперпозиции полей отдельных элементов. Это приводит к представлению суммарного поля в виде ряда. Линейное изменение фаз в элементах АР приводит к перемещению луча антенны в пространстве – сканированию. Антенны такого класса называются фазированными антенными решетками – ФАР. На практике находят применение линейные, плоские, осесимметричные (например, кольцевые) решетки.

4.1. Плоские решетки

Для формирования узконаправленного излучения в двух взаимно-перпендикулярных плоскостях и обеспечения возможностей управления лучом в некотором пространственном секторе углов необходимо использовать двумерную (поверхностную) решетку излучателей.

На практике находят применение поверхностные АР самой разнообразной формы и структуры. Однако, наибольшее распространение имеет АР, схема расположения элементов которой изображена на рис. 15.

Рис. 15. Плоская эквидистантная АР

Эта плоская решетка идентичных и одинаково ориентированных излучателей, расположенных в узлах прямоугольной эквидистантной сетки с периодом d_x и d_y.

Рассмотрим прямоугольную решетку с неравномерным амплитудным и линейным фазовым распределением, сфокусированную для ориентации луча под углами ₀, ₀. В этом случае распределение тока по элементам записывается как:

, (103)
где , , , . и – необходимые сдвиги фаз между соседними элементами в строке и столбце.

Проанализируем два частных случая амплитудного распределения токов в АР:

а) Закон распределения «Косинус на пьедестале»: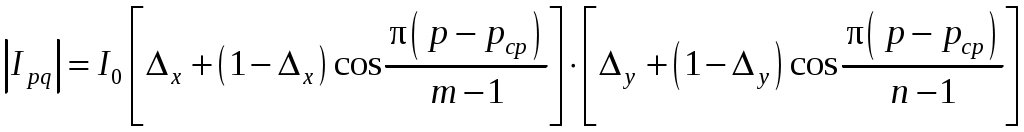
. (104)
ДН в этом случае определяется формулой: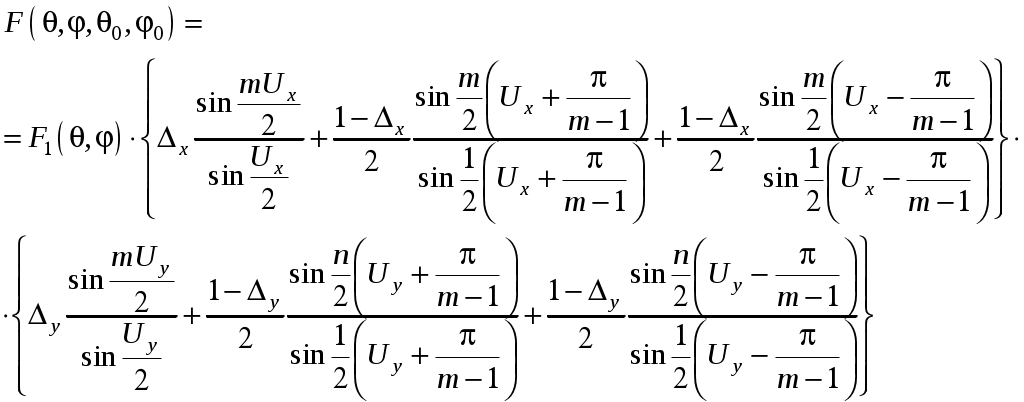
(105)
F₁(θ, φ) – ДН одиночного элемента.

б) Закон распределения «Косинус квадрат на пьедестале»:
.(106)

Выражение для ДН:
(107)
Для обоих законов распределения амплитуд:
(108)
Из формулы (104) следует частный случай равноамплитудного распределения ( ).

В двумерной решетке также как в линейной происходит расширение главного лепестка ДН при отклонении луча от нормали. Если решетка является остронаправленной ( 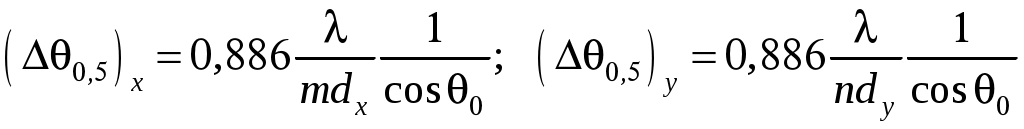), то можно считать, что расширение происходит лишь в плоскости сканирования. В этих случаях для ширины ДН справедливы приближенные формулы (равноамплитудные распределения):
, (109)
где – угол отклонения луча от нормали.

КНД ФАР с равномерным по амплитуде распределением определяется следующим выражением
. (110)