министерство образования и науки российской федерации Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
ИНТЕРФЕРОМЕТР МАЙКЕЛЬСОНА
Методические указания к выполнению лабораторной работы 3-11
по курсу «Общая физика» для студентов всех специальностей
Выполнил _________________
студент группы 5А16 (подпись)
________________
(дата)
Проверил: _______________
(подпись)
_______________
(дата)
Цель работы: изучить принцип действия интерферометра, определить длину волны лазера, определить зависимость коэффициента преломления воздуха от давления и показатель преломления стекла.
Приборы и принадлежности: интерферометр Майкельсона, гелий-неоновый лазер, ручной насос, вакуумная камера, стеклянная пластина.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Свет представляет собой электромагнитные волны. Плоскую электромагнитную волну, распространяющуюся по направлению вектора 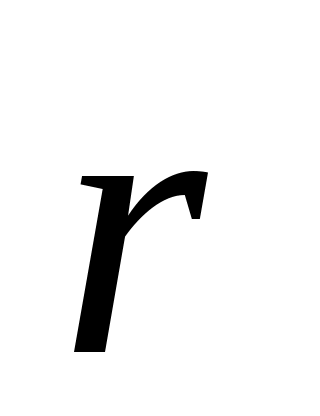 , можно описать уравнениями , можно описать уравнениями
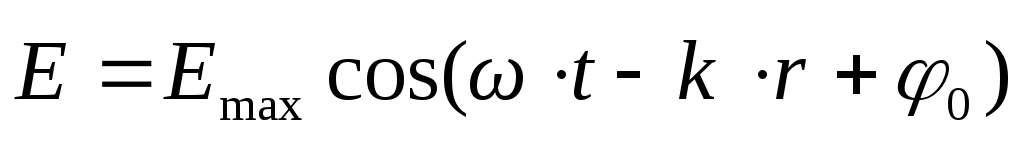 , (1) , (1)
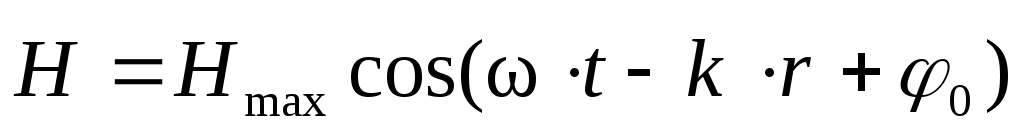 , (2) , (2)
где 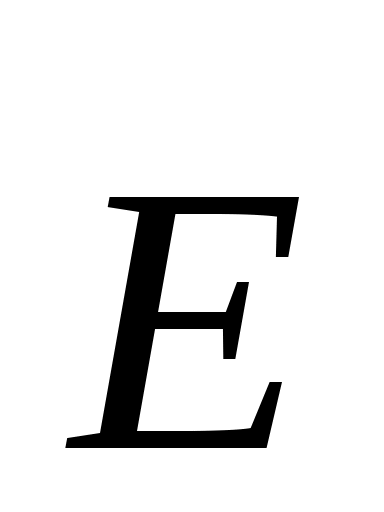 и и 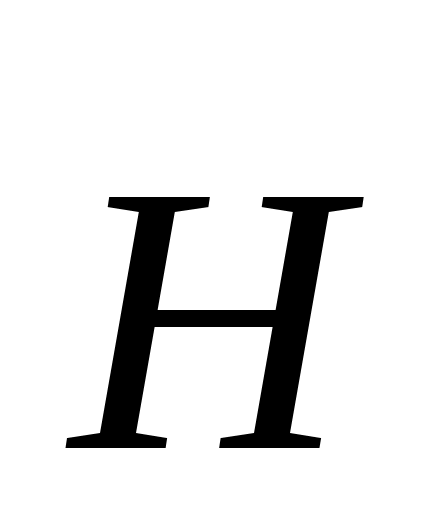 – векторы напряженности электрического и магнитного полей соответственно; – векторы напряженности электрического и магнитного полей соответственно; 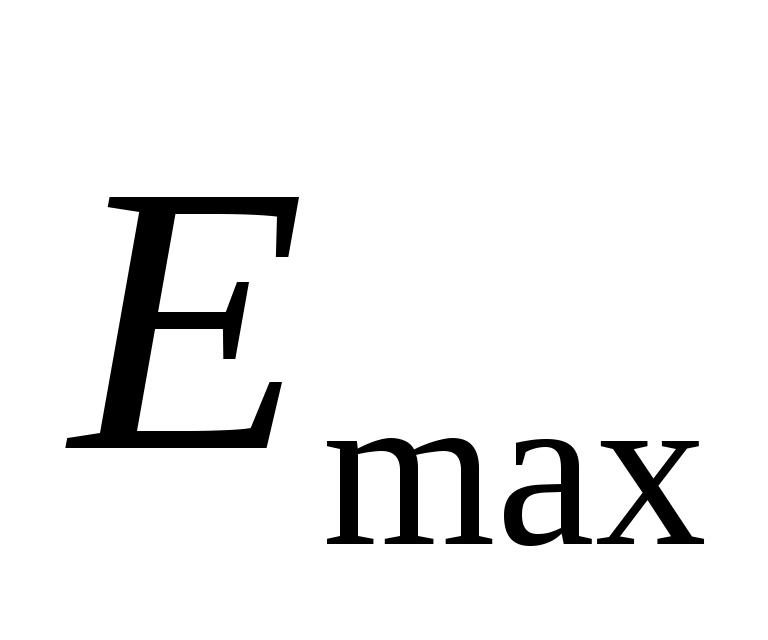 и и 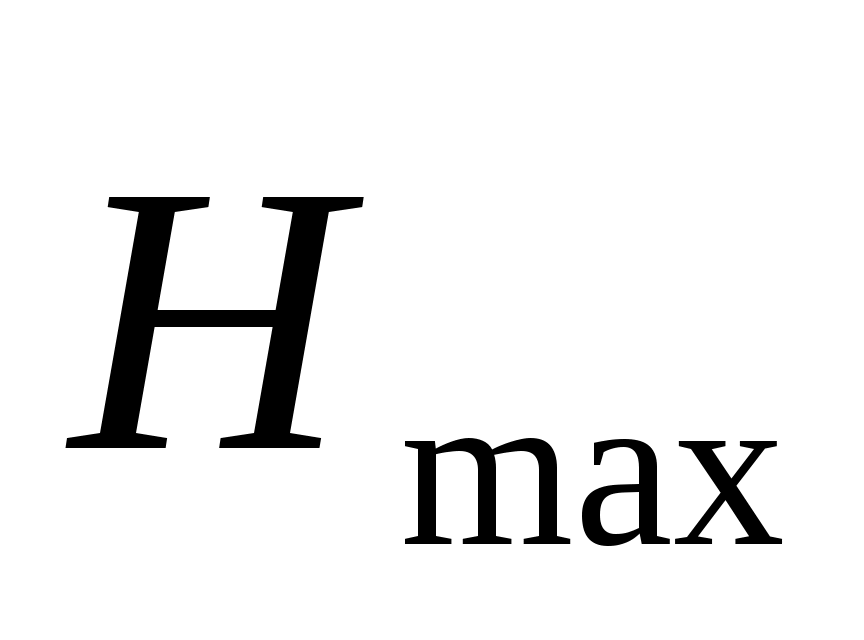 – их амплитудные значения; ω – циклическая частота волны; t – время; φo – начальная фаза; – их амплитудные значения; ω – циклическая частота волны; t – время; φo – начальная фаза; 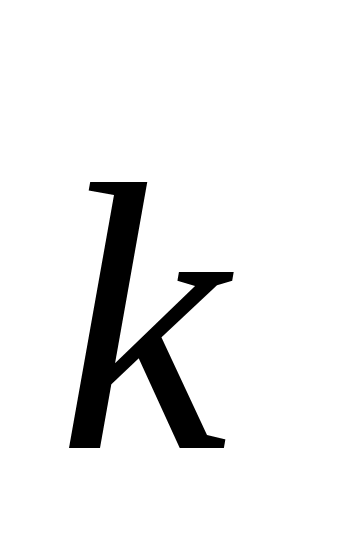 – волновой вектор, модуль которого равен – волновой вектор, модуль которого равен 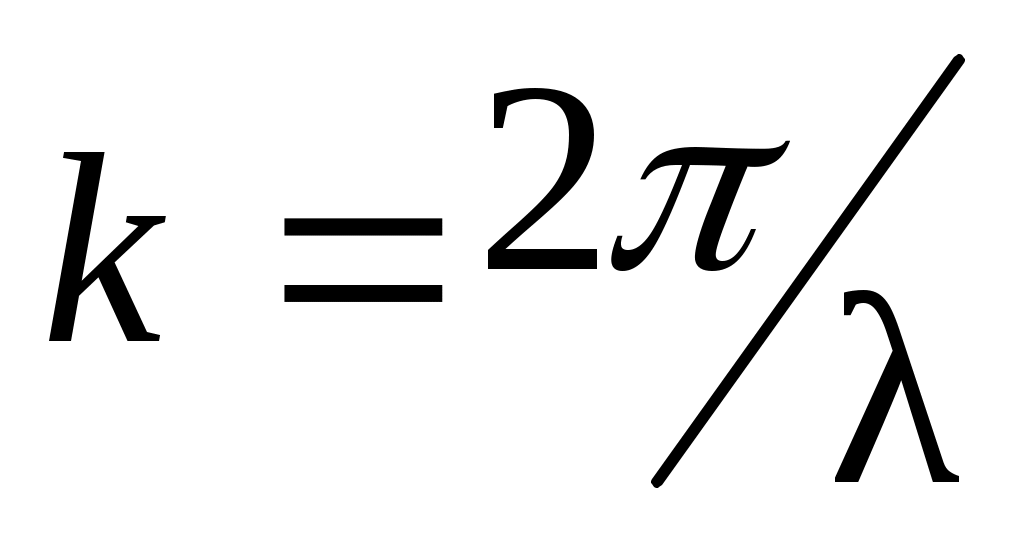 , а направление совпадает с направлением распространения волны; λ– длина волны. Поскольку практически все действия света определяются вектором , а направление совпадает с направлением распространения волны; λ– длина волны. Поскольку практически все действия света определяются вектором 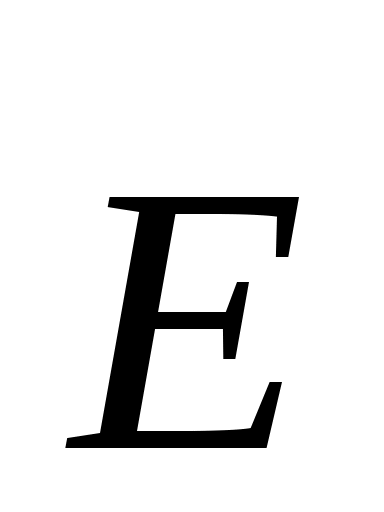 , то данный вектор называют световым вектором, а , то данный вектор называют световым вектором, а 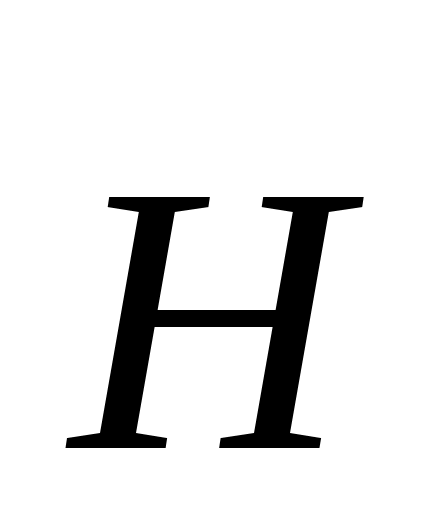 в оптических явлениях не учитывают. в оптических явлениях не учитывают.
Рассмотрим две волны одинаковой частоты, приходящие в одну точку P,
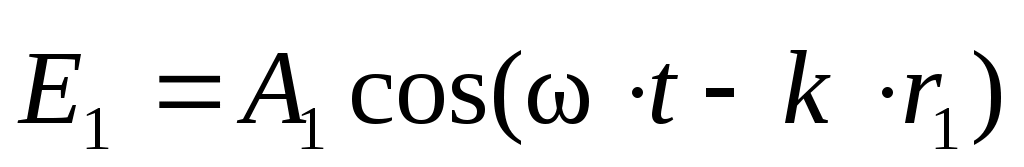 , (3) , (3)
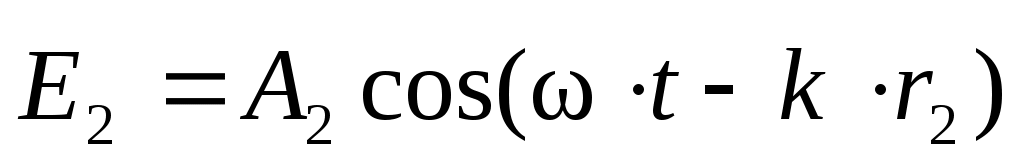 , (4) , (4)
где  и и 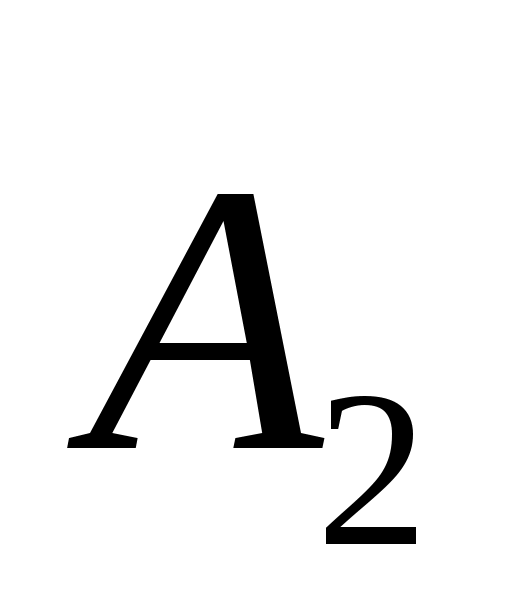 – модули амплитуд светового вектора первой и второй волны; – модули амплитуд светового вектора первой и второй волны; 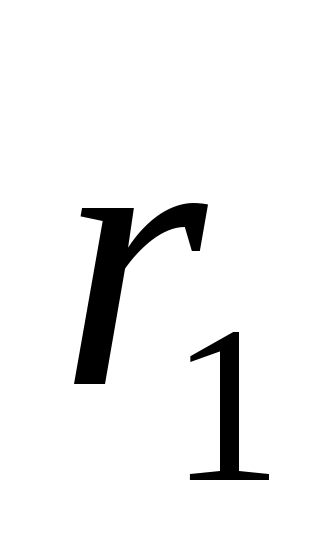 и и 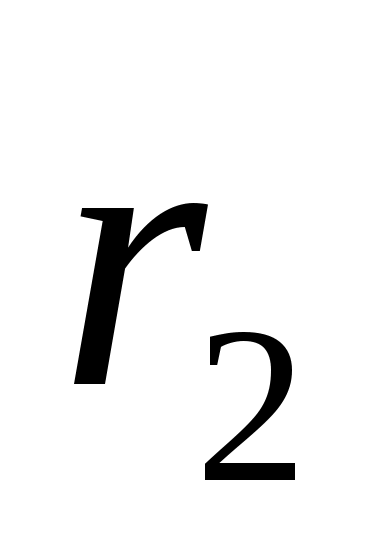 – расстояния, пройденные волнами до точки Р. В этой точке волны складываются, возбуждая результирующее колебание с амплитудой – расстояния, пройденные волнами до точки Р. В этой точке волны складываются, возбуждая результирующее колебание с амплитудой
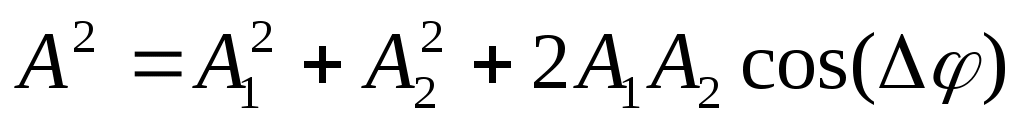 , (5) , (5)
где 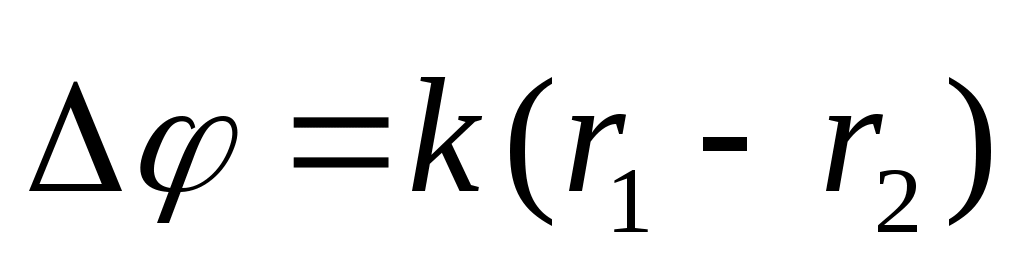 – разность фаз приходящих волн. – разность фаз приходящих волн.
Для наблюдения эффектов интерференции необходима взаимная когерентность волн, при которой разность фаз колебаний, возбуждаемых волнами в области их наложения, остается неизменной во времени, 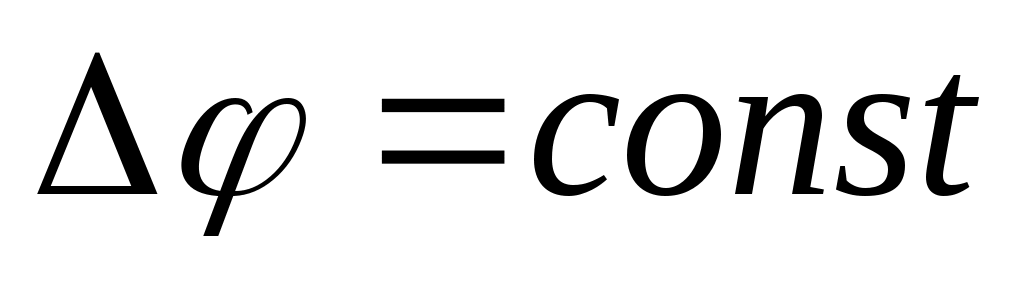 . .
Поскольку частота световой волны очень высока, то наблюдаемой величиной является интенсивность – среднее по времени значение плотности потока энергии, переносимого волной. Интенсивность света I пропорциональна квадрату амплитуды световой волны: I A2 . Тогда, исходя из (5), интенсивность света при наложении двух когерентных волн будет равна
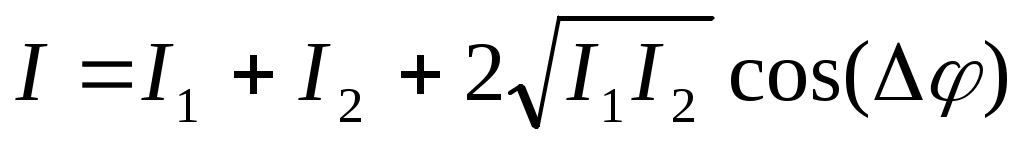 . (6) . (6)
Поскольку  имеет постоянное значение во времени, но разное в пространстве, интенсивность светового потока будет перераспределяться: в точках пространства, где складываются колебания, совпадающие по фазе имеет постоянное значение во времени, но разное в пространстве, интенсивность светового потока будет перераспределяться: в точках пространства, где складываются колебания, совпадающие по фазе 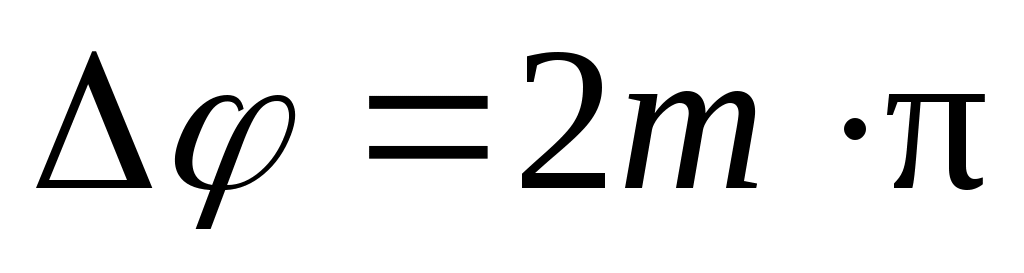 (m = 0,±1,±2,…), будут наблюдаться максимумы интенсивности, а в точках пространства, где суммирующиеся колебания оказываются в противофазе (m = 0,±1,±2,…), будут наблюдаться максимумы интенсивности, а в точках пространства, где суммирующиеся колебания оказываются в противофазе 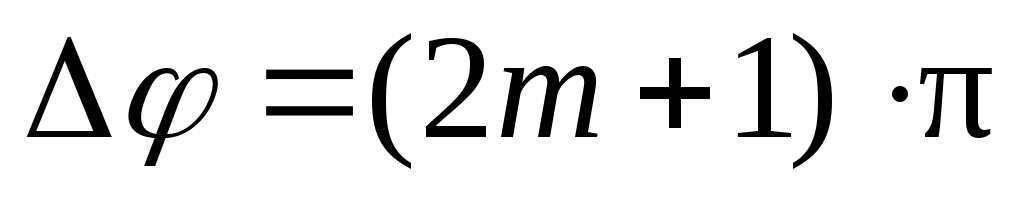 (m = 0,±1,±2,…), – минимумы. Явление перераспределения интенсивности в пространстве, связанное со сложением когерентных волн, называется интерференцией волн. В случае равных по интенсивности волн I1 = I2 в максимуме будет I = 4I1, в минимуме I = 0. (m = 0,±1,±2,…), – минимумы. Явление перераспределения интенсивности в пространстве, связанное со сложением когерентных волн, называется интерференцией волн. В случае равных по интенсивности волн I1 = I2 в максимуме будет I = 4I1, в минимуме I = 0.
Волны от физически различных источников взаимно некогерентны, поэтому для получения взаимно когерентных волн используют оптические устройства –интерферометры, в которых волну от одного источника разделяют на две волны, которые потом тем или иным способом накладывают друг на друга. Интерферометры можно разделить на два вида – с делением исходной волны по амплитуде и с делением по волновому фронту. К первому виду относятся интерферометры Ньютона, Физо, Майкельсона, Маха-Цендера, Жамена, Саньяка и другие, а ко второму виду – интерферометры Юнга, Релея, звездный интерферометр Майкельсона, бизеркала Френеля, бипризма Френеля, билинза Бийе, зеркало Ллойда и др.
В настоящей работе рассматриваются принцип действия и измерительные возможности интерферометра Майкельсона, получившего наиболее широкое распространение в измерительной технике и научных исследованиях. Принципиальная схема интерферометра Майкельсона представлена на рис. 1.
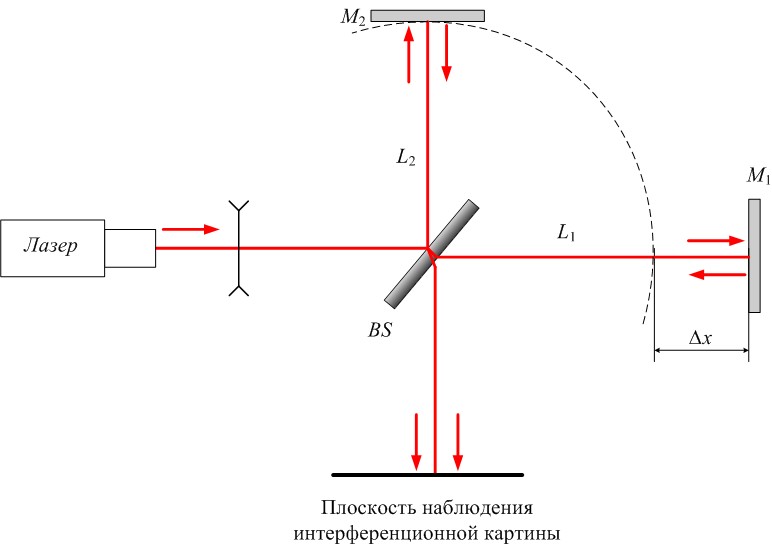
Рис. 1. Оптическая схема интерферометра Майкельсона:
BS – полупрозрачное зеркало (делитель исходного пучка света); M1 и M2 – плоские зеркала;
L1 и L2 – длины плеч интерферометра; ∆x=L1–L2 – разность длин плеч интерферометра
Световая волна от источника S делится полупрозрачным зеркалом BS (делителем) на две части – две волны, которые распространяются в направлениях перпендикулярных плоским зеркалам М1 и М2. Отраженные от зеркал волны возвращаются к делителю BS. Каждая из этих волн опять делится полупрозрачным зеркалом BS по амплитуде, так что в области между делителем и экраном складываются две волны. Результат интерференции этих волн можно наблюдать на экране в плоскости XY на некотором расстоянии от делителя BS.
Величина 2∆xназывается разностью хода волн. Если лучи проходят через среды с различными показателями преломления, например, n1и n2, то величина
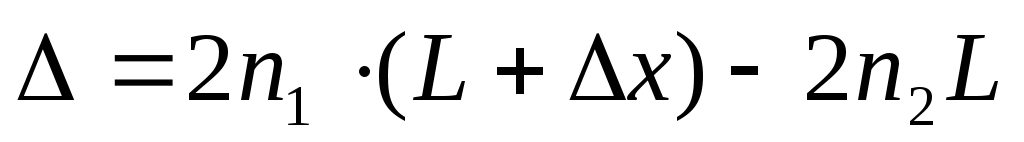 (7) (7)
есть оптическая разность хода волн. Оптической длиной путиназывается произведение расстояния L, пройденного светом в среде с показателем преломления n, на показатель преломления
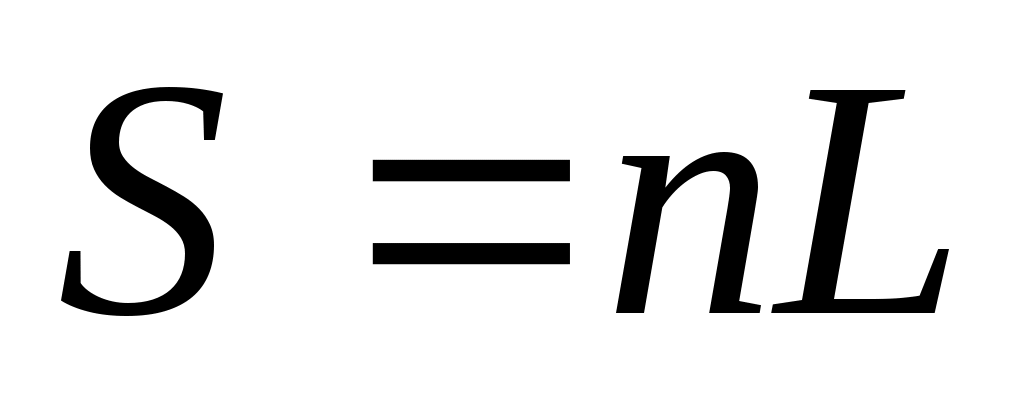 . (8) . (8)
Колебания, возбуждаемые волнами, идущими от делителя к экрану, будут усиливать друг друга, если оптическая разность хода волн в плечах интерферометра 2∆x равна целому числу длин волн λ(n1 = n2 = 1):
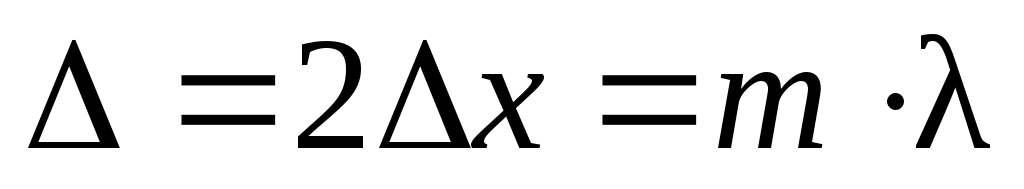 (9) (9)
и ослаблять друг друга, если разность хода равна нечетному числу длин полуволн
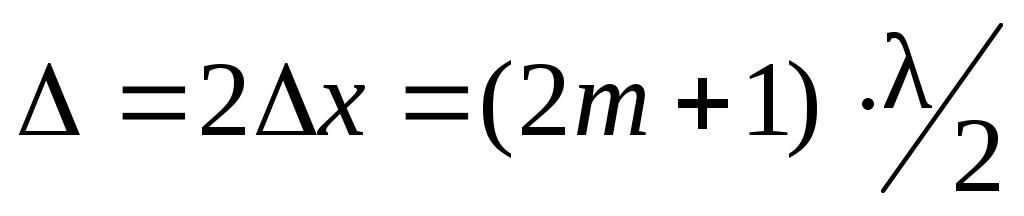 . (10) . (10)
В первом случае наблюдается максимум интерференции – светлая полоса, а во втором будет минимум интерференции – темная полоса.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
Внешний вид используемой в работе установки показан на рис. 2.
 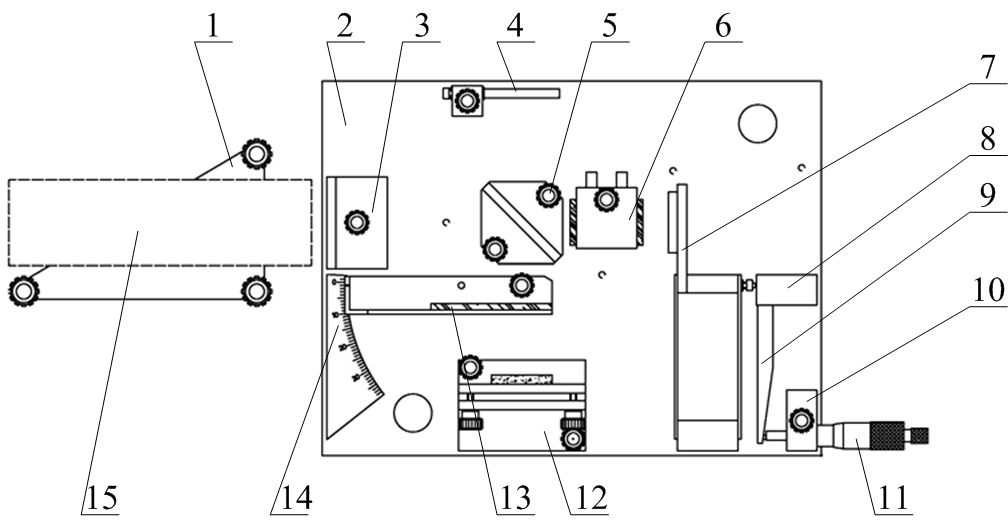
а б
Рис. 2. Интерферометр Майкельсона:
а) фотография интерферометра; б) схема интерферометра:
1 – держатель лазера; 2 – основание; 3 – рассеивающая линза; 4 – экран; 5 – делитель луча;
6 – вакуумная камера; 7 – подвижное зеркало; 8 – эксцентрик с калибровочной пластиной;
9 – плечо эксцентрика; 10 – держатель микрометрического винта;
11 – микрометрический винт; 12 – неподвижное зеркало; 13 – стеклянная пластина;
14 – шкала углов; 15 – лазер
Луч лазера 15, пройдя рассеивающую линзу 3, разделяется на два с помощью полупрозрачного зеркала, делителя луча 5 (рис. 2, б). Пройдя некоторый путь, один луч отражается от неподвижного зеркала 12, второй луч – от подвижного зеркала 7, положение которого можно менять с помощью микрометрического винта 11. После этого лучи возвращаются вдоль своих траекторий на полупрозрачное зеркало 5 и идут на экран 4, где в результате их сложения наблюдается интерференционная картина – чередующиеся светлые и темные кольца.
ОПРЕДЕЛЕНИЕ ДЛИНЫ ВОЛНЫ ЛАЗЕРА
Если переместить зеркало 7 (рис. 2, б), снабженное механизмом точной регулировки, на величину ∆x, оптическая разность хода лучей изменится на величину ∆S. При этом на экране 4 интерференционные полосы будут смещаться. Поскольку луч дважды проходит расстояние ∆x, то ∆S = 2∆x∙n, где n= 1 – показатель преломления воздуха.
Зная количество линий m, на которые сместилась интерференционная картина, можно найти длину волны лазера, используя уравнение (9)
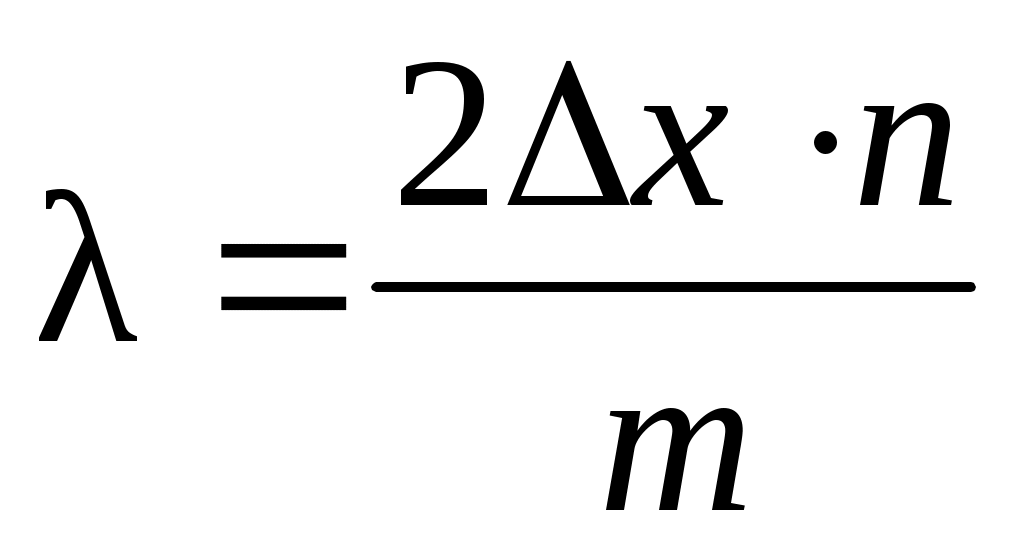 . (11) . (11)
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ВОЗДУХА ПРИ НОРМАЛЬНОМ ДАВЛЕНИИ
Из уравнений Максвелла следует, что скорость электромагнитных волн равна
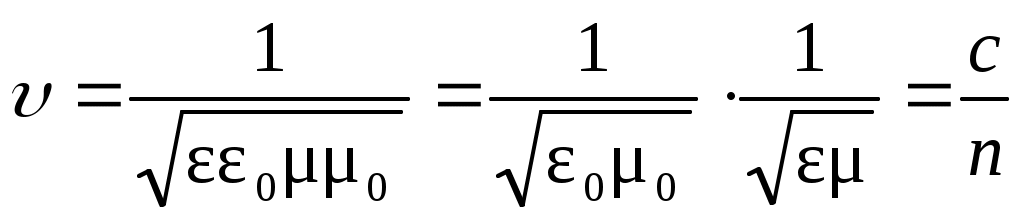 , (12) , (12)
где 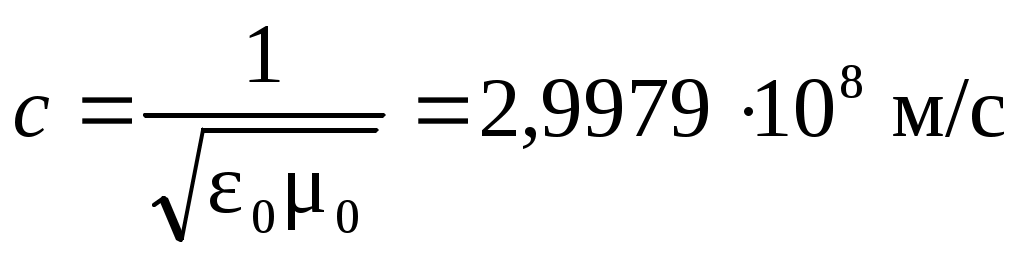 – скорость света в вакууме; – скорость света в вакууме; 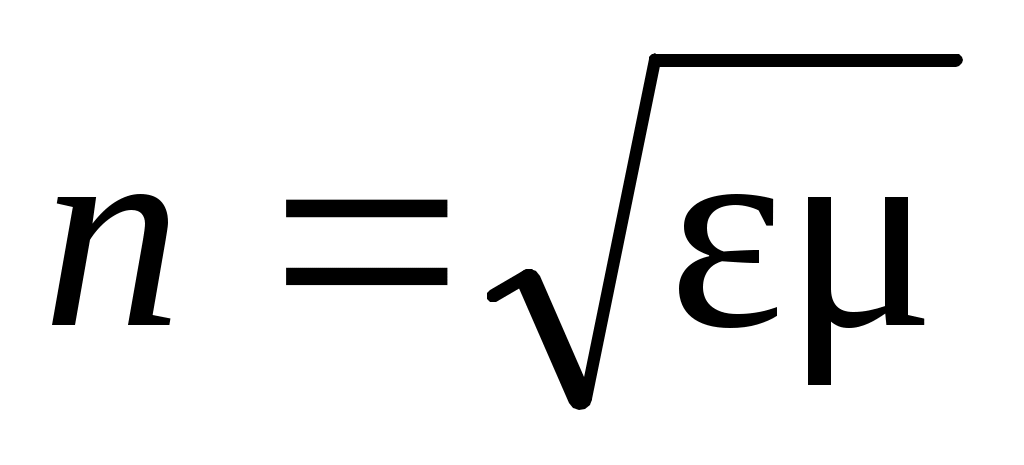 – показатель преломления среды; εо = 8,85∙10-12 Ф/м – электрическая постоянная; μо = 4π∙10-7 Гн/м – магнитная постоянная; εи μ – диэлектрическая и магнитная проницаемости среды, соответственно. Поскольку для воздуха μ = 1, то показатель преломления – показатель преломления среды; εо = 8,85∙10-12 Ф/м – электрическая постоянная; μо = 4π∙10-7 Гн/м – магнитная постоянная; εи μ – диэлектрическая и магнитная проницаемости среды, соответственно. Поскольку для воздуха μ = 1, то показатель преломления 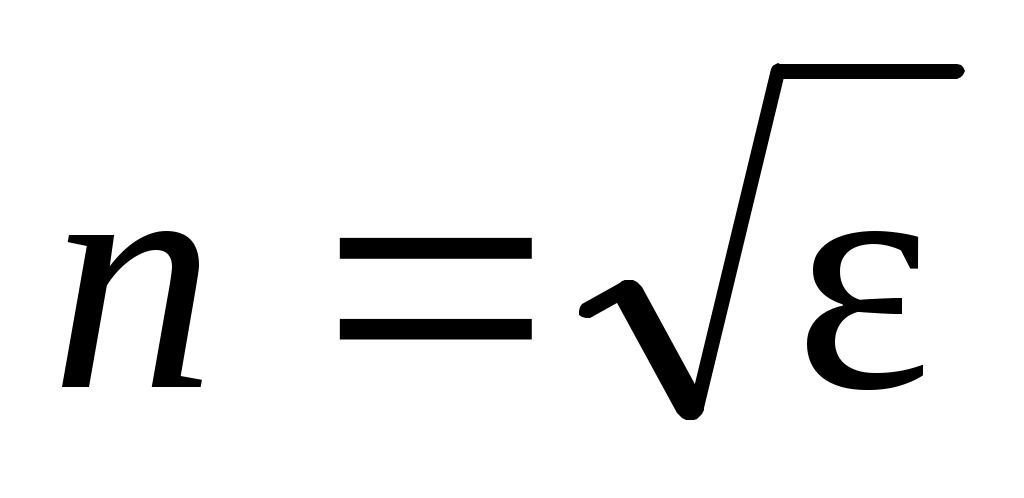 . .
В соответствии с классической теорией дисперсии молекулы среды можно рассматривать как систему, в которую входят электроны, находящиеся в положении равновесия. Под действием внешнего периодического поля волны, электроны смещаются из положения равновесия, при этом атом приобретает электрический момент.
Электрическое смещение (электрическая индукция) среды определяется соотношением
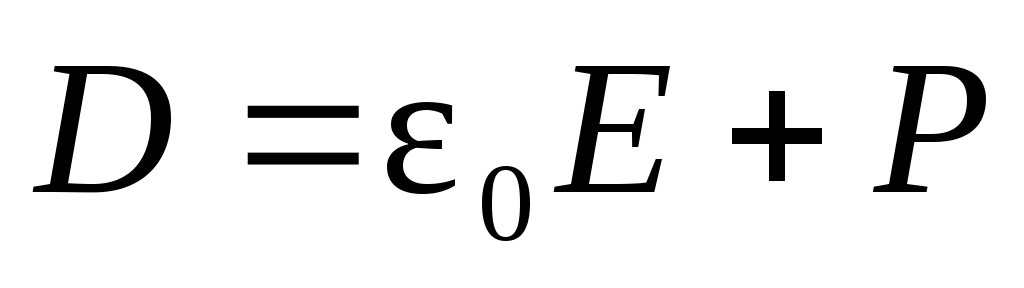 , (13) , (13)
где 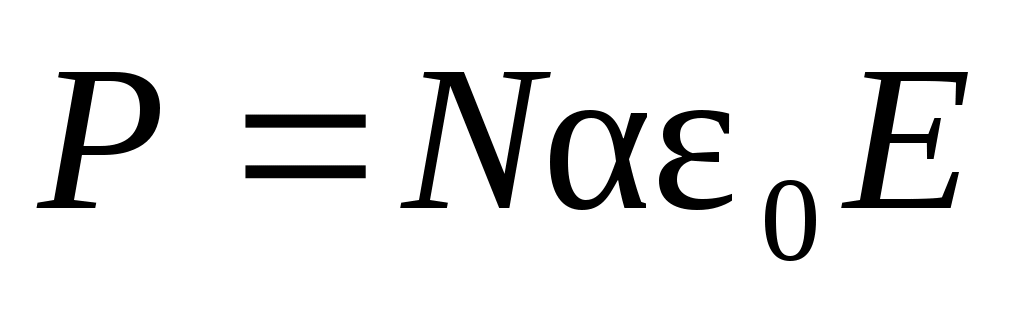 – электрический момент, приобретаемый единицей объема среды под действием внешнего поля Е; α – поляризуемость молекул, зависящая от их строения; N – концентрация молекул. Электрическое смещение D и напряженность поля E связаны – электрический момент, приобретаемый единицей объема среды под действием внешнего поля Е; α – поляризуемость молекул, зависящая от их строения; N – концентрация молекул. Электрическое смещение D и напряженность поля E связаны
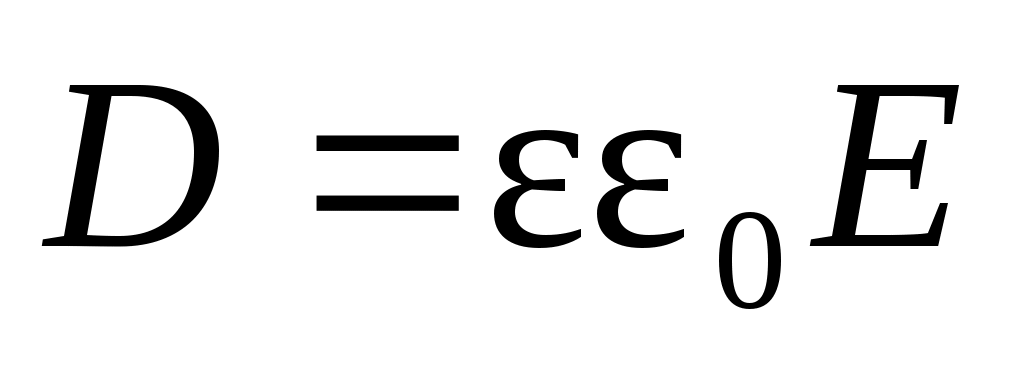 . (14) . (14)
Тогда из соотношения (13) можно получить следующее соотношение для диэлектрической проницаемости среды:
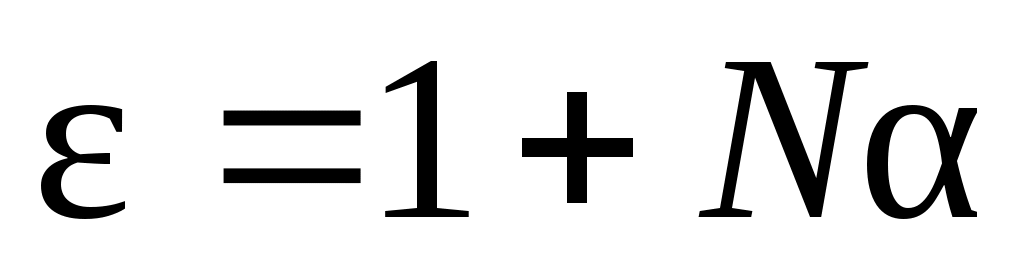 , (15) , (15)
а для коэффициента преломления:
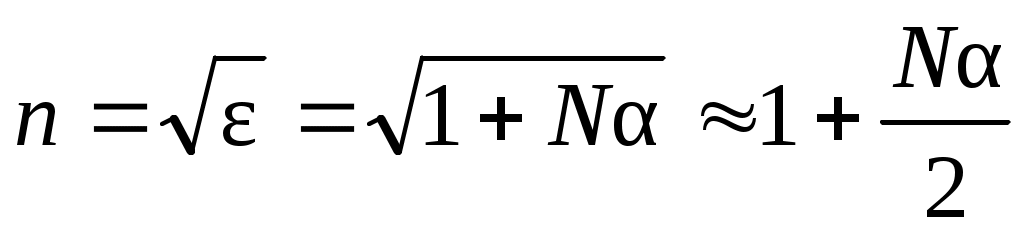 . (16) . (16)
Из молекулярно-кинетической теории давление р связано с температурой Т
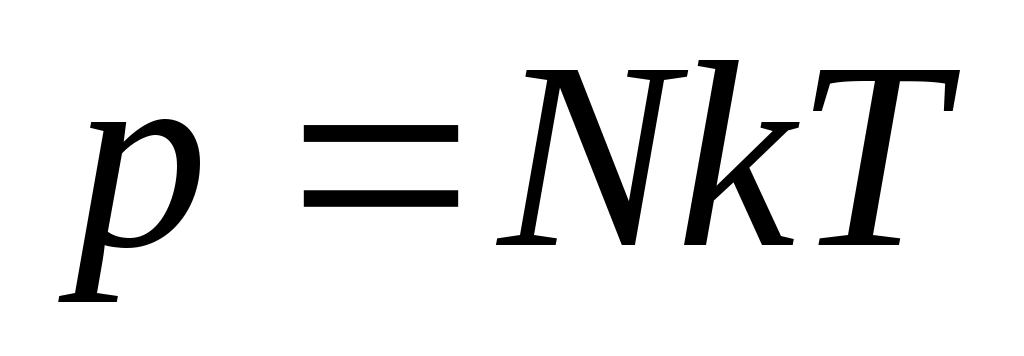 , (17) , (17)
где k – постоянная Больцмана. Тогда показатель преломления будет определяться как
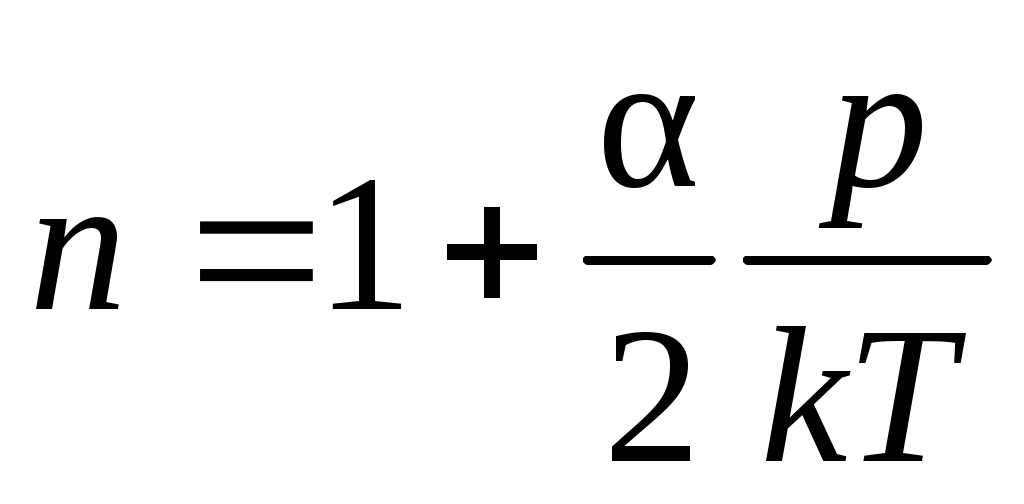 . (18) . (18)
Таким образом, при постоянной температуре зависимость показателя преломления среды от давления линейная:
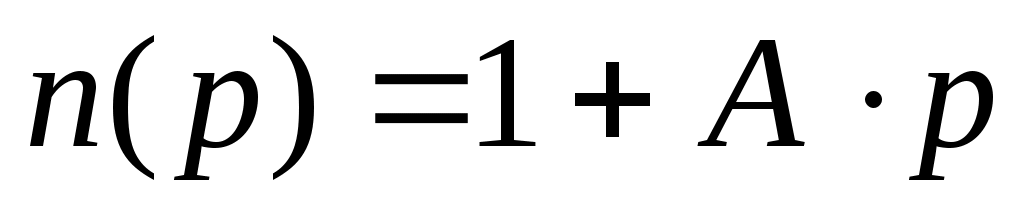 , (19) , (19)
здесь коэффициент 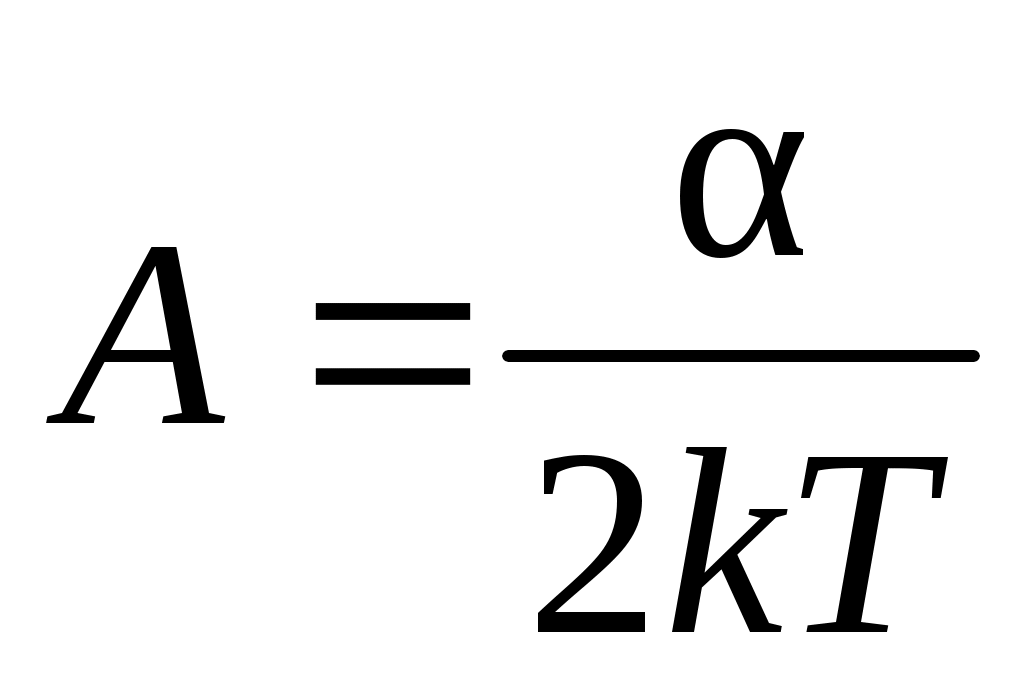 . .
Поместим на пути одного из лучей, например, идущего к подвижному зеркалу, камеру длиной d (рис. 3), заполненную воздухом при давлении p1, а затем накачаем в нее воздух до давления р2.
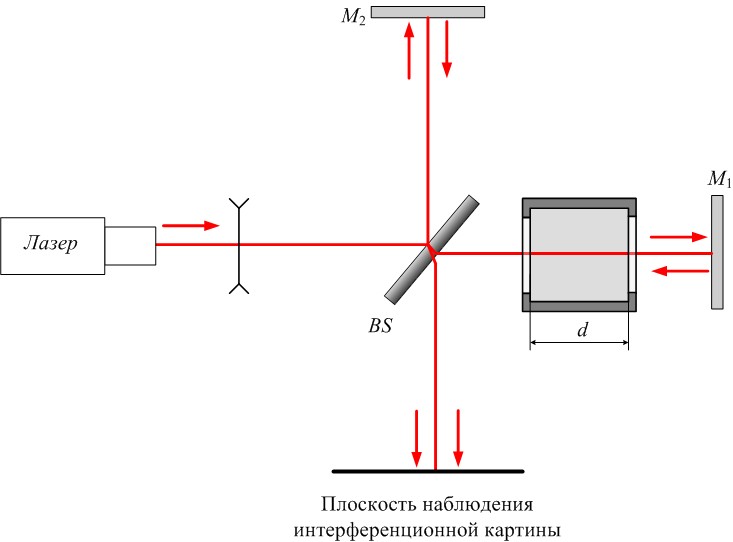
Рис. 3. Оптическая схема интерферометра Майкельсона с установленной вакуумной камерой длиной d
Представим оптическую длину пути этого луча при давлении p1 в камере как
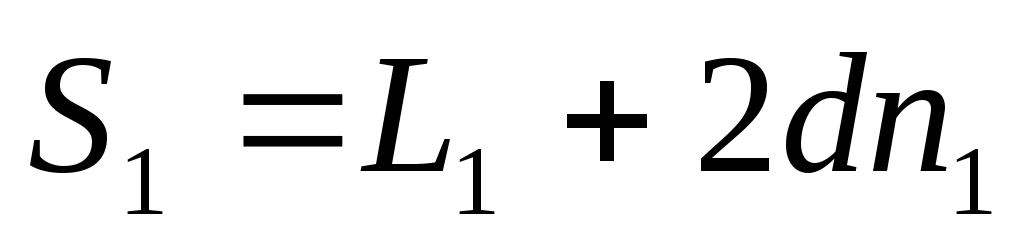 , (20) , (20)
где L1 – весь оптический путь луча вне камеры, а 2dn1 – оптический путь луча в камере. При давлении p2 (L1 не меняется)
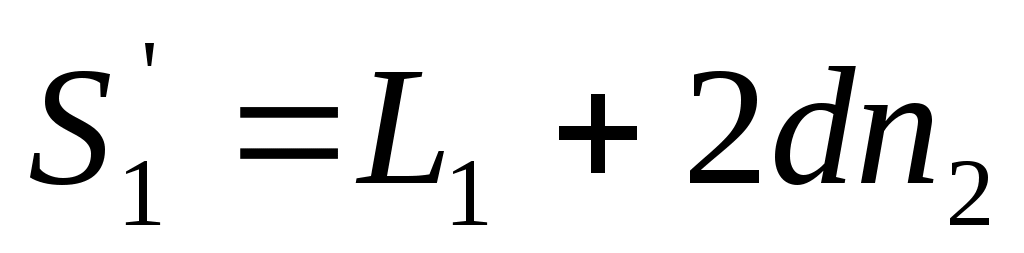 . (21) . (21)
Таким образом, при изменении давления от p1 до p2 в разность хода интерферирующих лучей вносится дополнительная разность хода
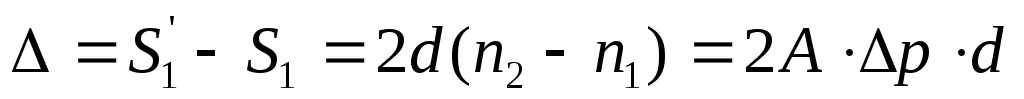 . (22) . (22)
Здесь 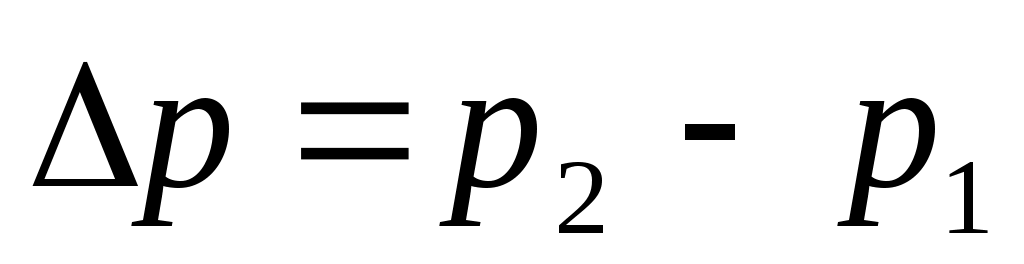 ; n1 и n2 – показатели преломления при давлениях p1 и p2, соответственно. ; n1 и n2 – показатели преломления при давлениях p1 и p2, соответственно.
При этом интерференционная картина сместится на ∆m линий, и разность хода станет
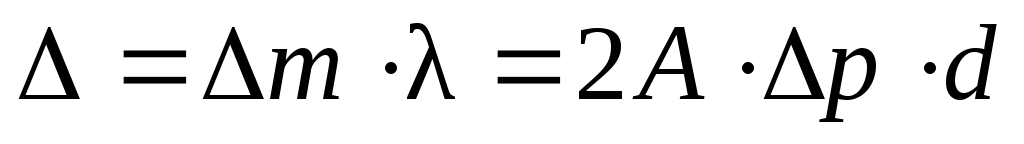 . (23) . (23)
Откуда получаем, что зависимость между числом линий и давлением равна
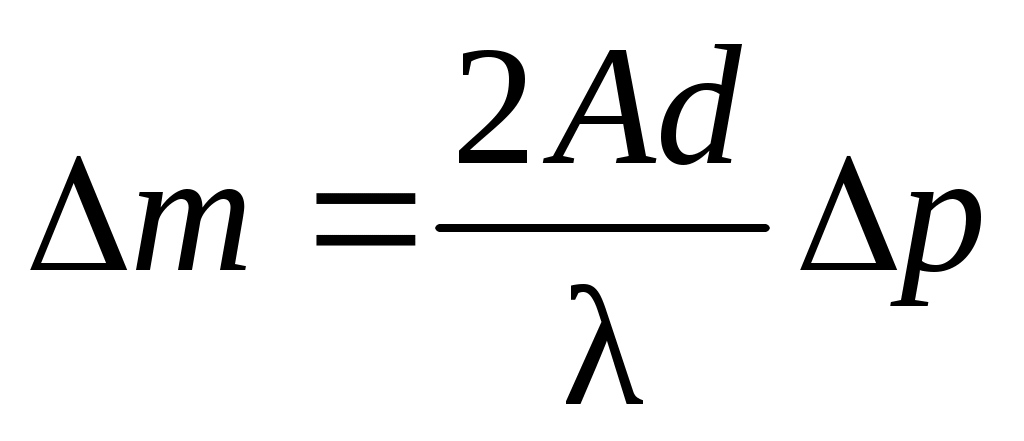 (24) (24)
Величина 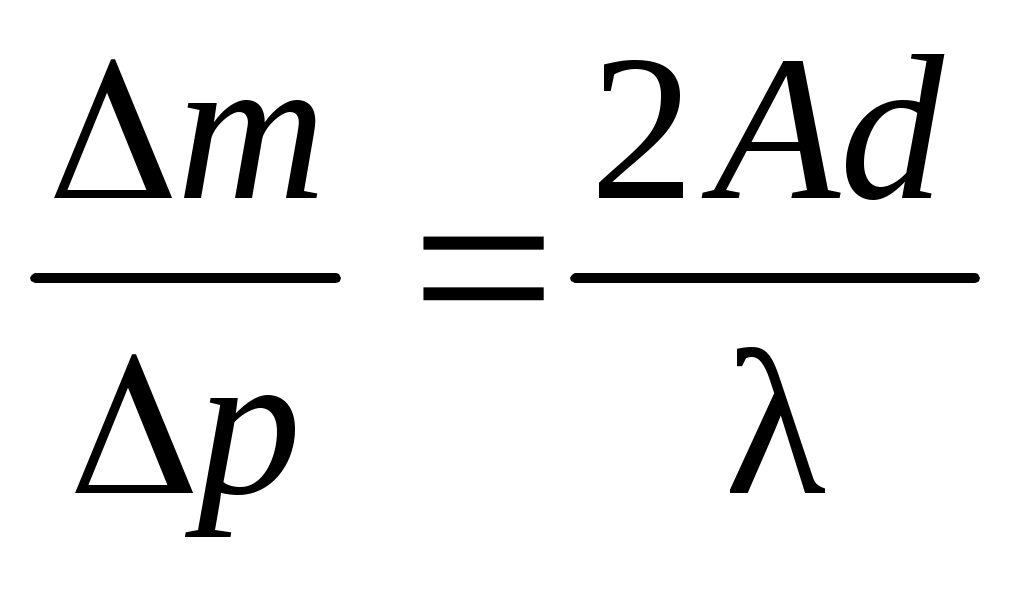 является угловым коэффициентом прямой зависимости числа новых интерференционных полос ∆m от изменения давления ∆p и численно равна тангенсу угла наклона этой прямой. Определив угловой коэффициент из графика зависимости ∆m(p), можно найти постоянную А, при известных параметрах dи λ: является угловым коэффициентом прямой зависимости числа новых интерференционных полос ∆m от изменения давления ∆p и численно равна тангенсу угла наклона этой прямой. Определив угловой коэффициент из графика зависимости ∆m(p), можно найти постоянную А, при известных параметрах dи λ:
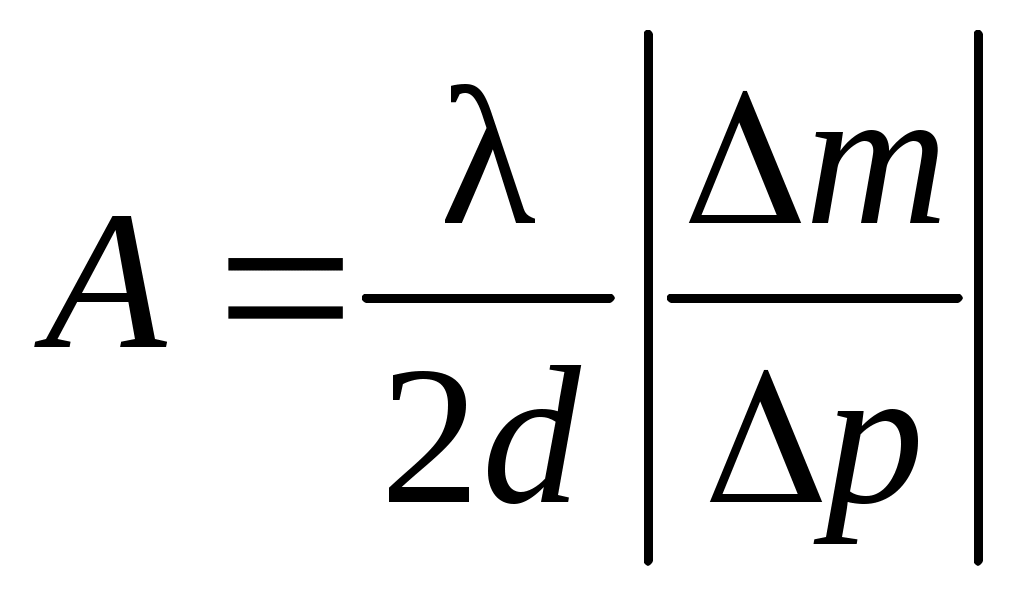 . (25) . (25)
Зная коэффициент А, можно рассчитать коэффициент преломления воздуха при нормальном давлении pо = 101325 Па
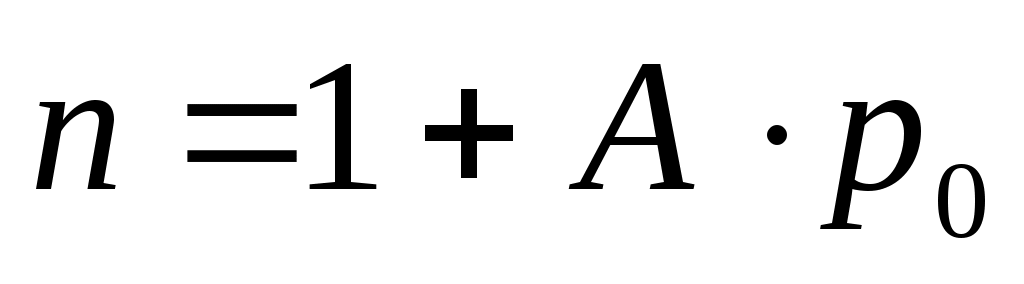 . (26) . (26)
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ СТЕКЛА
Поместим на пути одного из лучей, например, идущего к неподвижному зеркалу, стеклянную пластинку толщиной t(рис. 4).
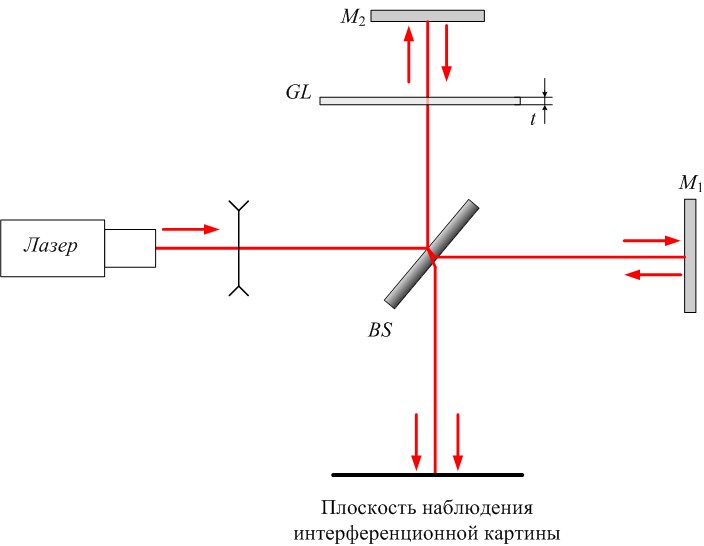
Рис. 4. Оптическая схема интерферометра Майкельсона с установленной стеклянной пластиной GL толщиной t
Представим оптическую длину пути этого луча без стекла
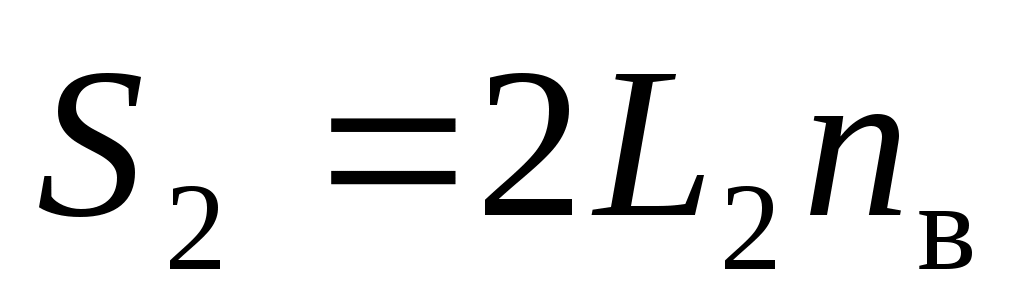 , (27) , (27)
где L2 – путь луча в плече без стекла, а nв = 1 – показатель преломления воздуха. При добавлении стеклянной пластинки на пути луча получаем
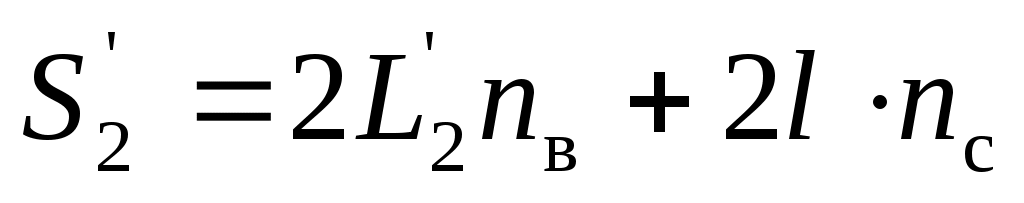 , (28) , (28)
где L2’ – путь луча, пройденный вне стеклянной пластинки, l – путь луча, пройденный в стеклянной пластинке, nc – показатель преломления стекла. Если угол падения α луча на пластинку составляет 00, то l = t и оптическую разность хода можно определить как:
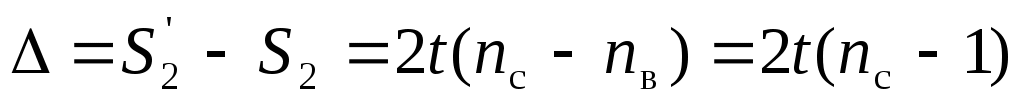 . (29) . (29)
Рассмотрим случай, когда угол падения α луча на пластинку отличен от 00 (рис. 5), т.е. l ≠ t.
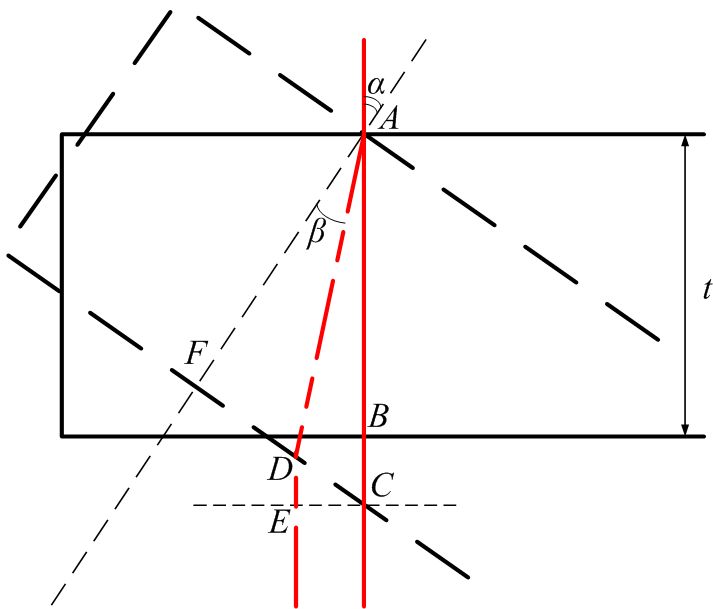
Рис. 5. Оптический путь луча лазера в зависимости от его угла падения на пластинку
При α = 00 оптический путь луча можно записать в виде (nв = 1)
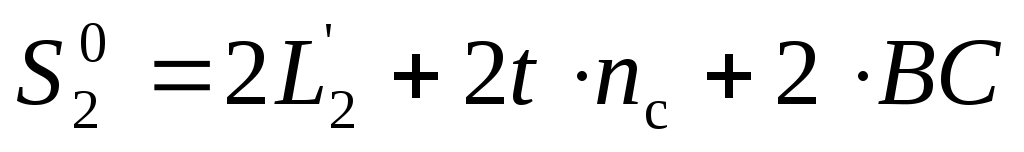 . (30) . (30)
Здесь L2’ – путь луча, пройденный вне отрезка AC.
При α ≠ 900 оптический путь луча составит
 . (31) . (31)
Таким образом, оптическая разность хода луча при повороте пластинки на угол α:
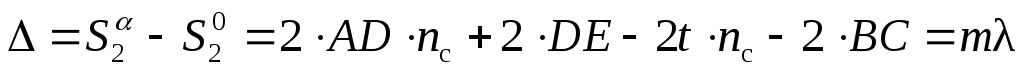 . (32) . (32)
Здесь m – число появившихся или исчезнувших при повороте пластинке интерференционных полос.
Учитывая, что
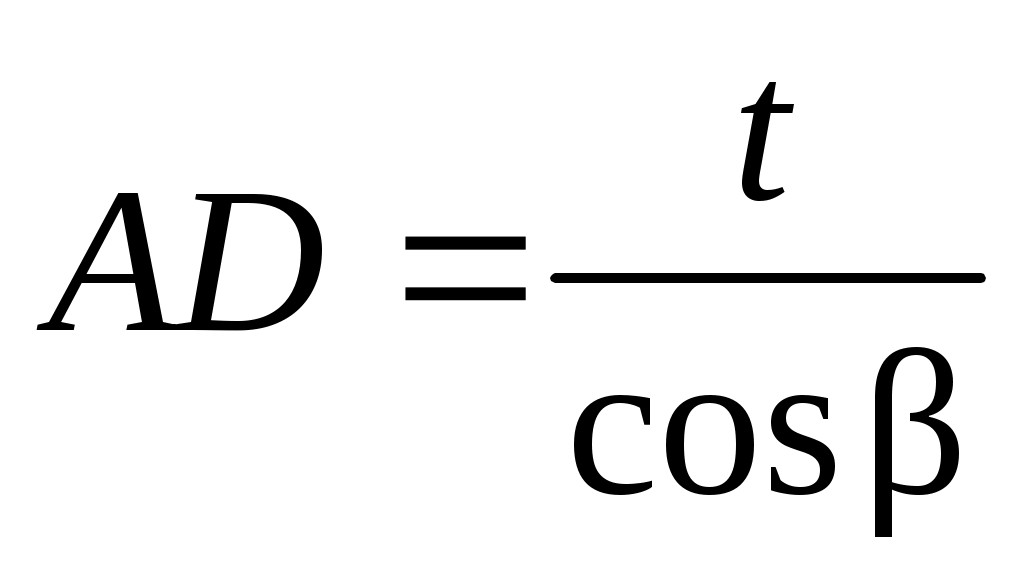 , (33) , (33)
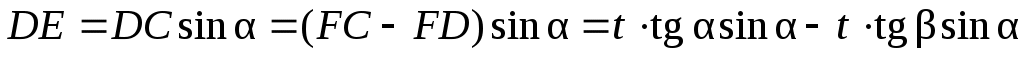 , (34) , (34)
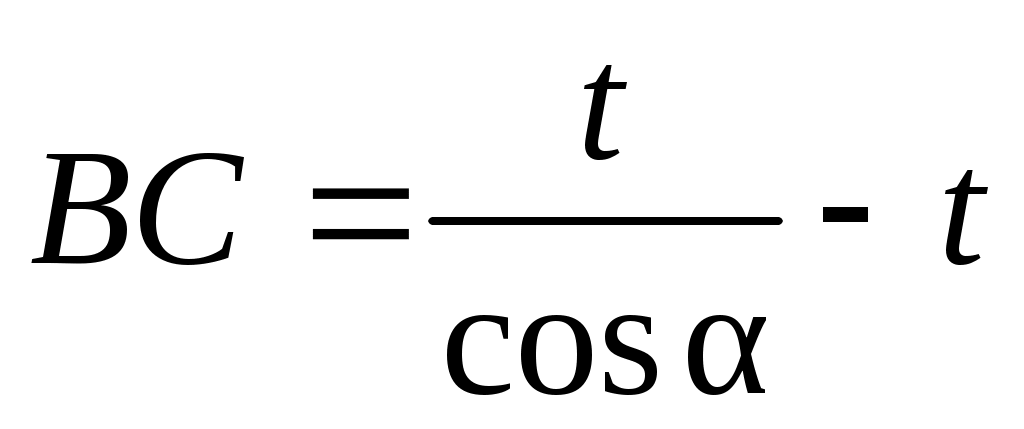 , (35) , (35)
получаем
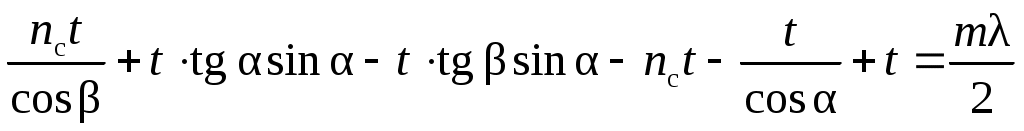 . (36) . (36)
Используя закон Снеллиуса преломления света 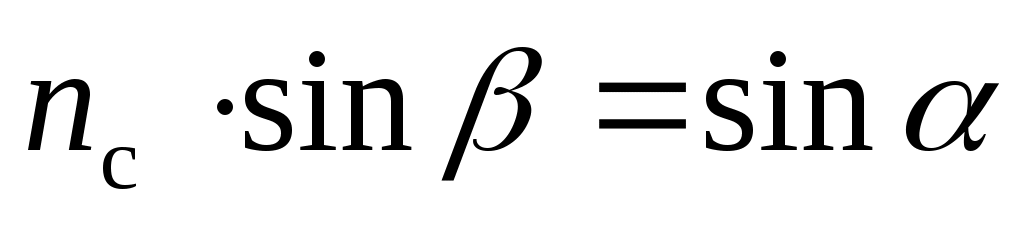 , уравнение (36) можно свести к виду , уравнение (36) можно свести к виду
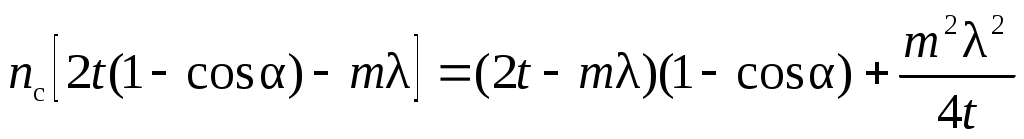 . (37) . (37)
Таким образом, показатель преломления стекла можно определить как
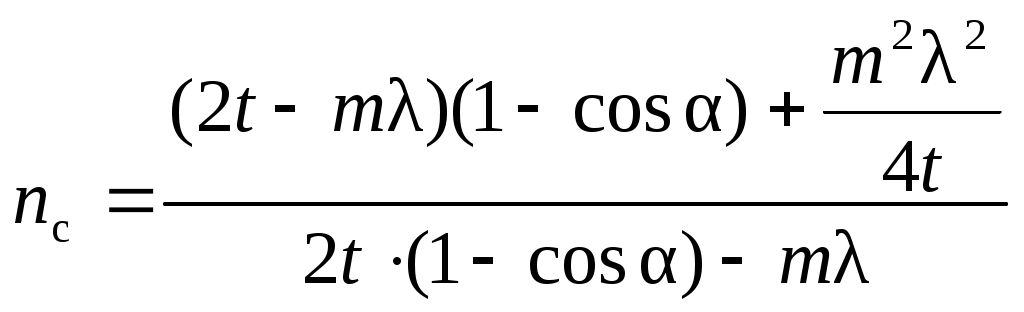 . (38) . (38)
ОПРЕДЕЛЕНИЕ ДЛИНЫ ВОЛНЫ ЛАЗЕРА:
Поверните микрометрический винт на 25 мм назад (против часовой стрелки), а затем медленно поверните его по часовой стрелке в нулевое положение x(0) = 20,00 мм.
Зафиксируйте на экране положение темного или светлого кольца (для этого на экране имеется миллиметровая шкала).
Поворачивайте микрометрический винт по часовой стрелке до появления в отмеченной точке 30 абсолютно новых (темных или светлых) интерференционных полос.
Отметьте это положение x(30) на микрометрическом винте и запишите результат.
Повторите опыт три раза, занесите данные в таблицу 1.
Таблица 1
№
|
x(0), мм
|
x(30), мм
|
∆x, мкм
|
∆xср, мкм
|
λ, нм
|
1
|
|
|
|
|
|
2
|
|
|
|
3
|
|
|
|
Рассчитайте смещение ∆x подвижного зеркала (коэффициент уменьшения движения 1:813): ∆x =[x(0) – x(30)]/813.
Найдите длину волны лазера.
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ВОЗДУХА ПРИ НОРМАЛЬНОМ ДАВЛЕНИИ:
Установите камеру с присоединенным насосом на путь луча, идущего к подвижному зеркалу (рис. 2).
Отрегулируйте неподвижное зеркало так, чтобы интерференционные кольца оставались в центре экрана.
Зафиксируйте на экране положение темного или светлого кольца. Считайте его номером m = 0.
Таблица 2
∆m
|
∆p, кПа
|
p, кПа
|
0
|
0
|
100
|
3
|
…
|
…
|
6
|
…
|
…
|
…
|
…
|
…
|
27
|
…
|
…
|
Медленно откачивая воздух из камеры, фиксируйте число m приходящих в отмеченную точку темных или светлых полос и с регулярными интервалами заносите результаты вместе с соответствующими значениями изменения давления ∆p в вакуумной камерев таблицу 2. Шкала манометра проградуирована в мбар: 1 бар = 105 Па.
Постройте график зависимости ∆m(p), определите угловой коэффициент (тангенс угла наклона) данной зависимости.
Найдите константу А, и коэффициент преломления воздуха при нормальном давлении. (Путь луча внутри камеры d = 41 мм.)
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ СТЕКЛА:
Установите перпендикулярно лучу лазера, идущему к неподвижному зеркалу, стеклянную пластину (рис. 2).
Отрегулируйте неподвижное зеркало так, чтобы интерференционные кольца оставались в центре экрана.
Зафиксируйте на экране положение темного или светлого кольца.
Медленно поворачивая стеклянную пластину, определите угол падения луча α, при котором через отмеченную на экране точку пройдет m = 20 темных или светлых полос.
Повторите опыт три раза, данные занесите в таблицу 3.
Рассчитайте показатель преломления стекла nc. Толщина пластинки t= 4 мм.
Таблиц 3
№
|
α, град
|
αср, град
|
nc
|
1
|
|
|
|
2
|
|
3
|
|
|
 Скачать 0.51 Mb.
Скачать 0.51 Mb.






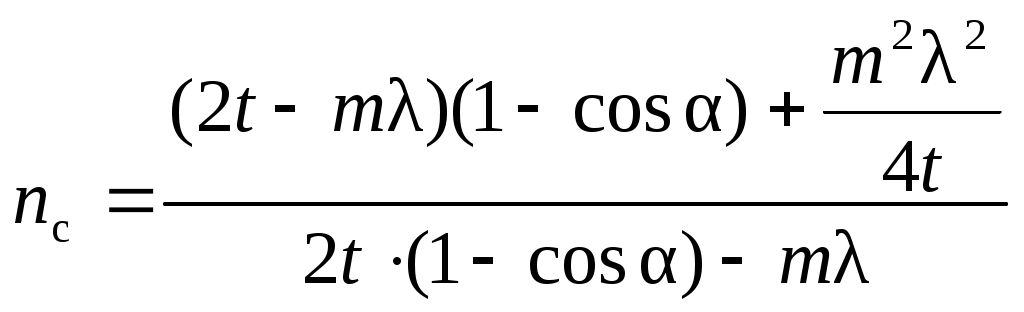 . (38)
. (38)