Расчетно-графическая работа. Методичка РГР. Методические указания к выполнению расчетнографической работы по дисциплине статистика омск 2020 Содержание Введение 3

• Название: Методические указания к выполнению расчетнографической работы по дисциплине статистика омск 2020 Содержание Введение 3
• Анкор: Расчетно-графическая работа
• Дата: 14.06.2021
• Размер: 418.5 Kb.
• Имя файла: Методичка РГР.doc
• Тип: Методические указания; #217327
• страница: 6 из 6

φ(х), объясняющей основную закономерность влияния факторного признака х на результативный признак у.

Под формой статистической связи понимают ту тенденцию, которая проявляется в изменении изучаемого результативного признака в связи с изменением факторного признака. Форму связи можно попытаться установить, построив в прямоугольной системе координат все множество пар значений признаков (х_i, у_i), . По оси абсцисс откладываются значения факторного признака х, по оси ординат – значения признака у. Такое графическое построение называется полем корреляции или диаграммой рассеяния, пример построения представлен на рис. 2. По характеру расположения точек на координатной плоскости можно судить о характере статистической связи. Если наблюдается тенденция равномерного возрастания или убывания значений признака, то связь называется прямолинейной. При тенденции неравномерного изменения значений зависимость носит название криволинейной.

Линия на графике (см. рис. 2), изображающая тенденцию в изменении результативного признака при возрастании факторного, называется линией регрессии.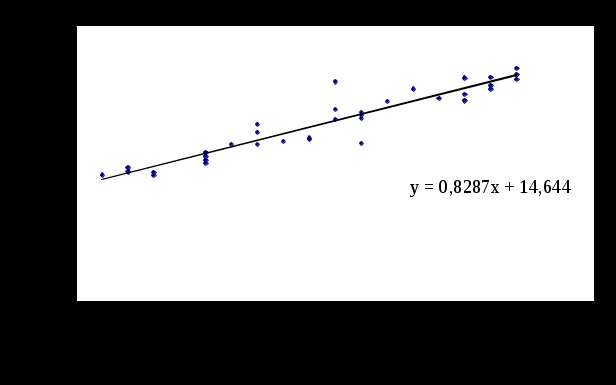



Рисунок 2 – Диаграмма рассеяния и линия регрессии
В случае прямолинейной связи линия регрессии ищется в виде уравнения прямой линии:

, (8)
где у – теоретические значения результативного признака, образующие прямую линию; а₀, а₁ – параметры уравнения; х – значения факторного признака.

Расчет параметров уравнения производится методом наименьших квадратов. В основу метода положено требование минимальности отклонения теоретических значений у’_i от эмпирических (полученных в результате наблюдения) значений признака у_i при одном и том же значении х_i. Это требование в математических обозначениях записывается следующим образом:

. (9)
Подставляя вместо теоретических значений их запись через параметры а₀ и а₁ , получаем
. (10)
В этом выражении известны все х_i и у_i, полученные в результате наблюдения, неизвесты лишь а₀ и а₁. Полученная функция двух переменных а₀ и а₁ имеет минимум, когда частные производные 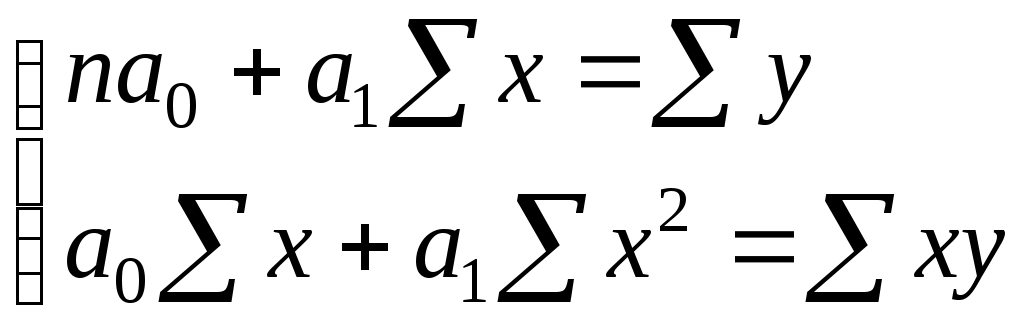и одновременно равны 0. Произведя дифференцирование по а₀ и а₁, получаем систему двух уравнений с двумя неизвестными:
(11)
где n – общее число наблюдений; х, у – значения признаков, полученные в результате наблюдения.

Решая данную систему уравнений, получим выражение для нахождения коэффициентов а₀ и а₁: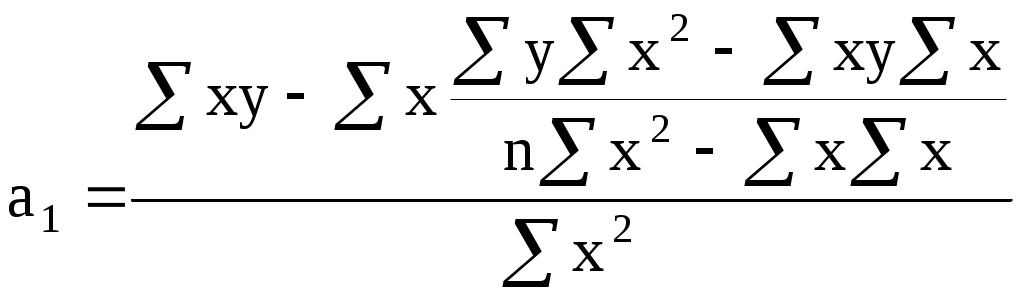
, (12)
, (13)
где n – общее число наблюдений; х, у – значения признаков, полученные в результате наблюдения.

Рассмотрим значения коэффициентов, полученных при расчете. Параметр а₁ в уравнении регрессии называется коэффициентом регрессии. Коэффициент регрессии показывает среднее изменение результативного признака у при увеличении факторного признака х на единицу. Например, получив уравнение прямолинейной связи: у = 20,5 + 1,3х, можно утверждать, что с увеличением признака х на единицу у увеличивается в среднем на 1,3 единицы. По отношению к статистическим данным, представленным в задании на РГР, такое уравнение показывает, что при увеличении возраста станка на один год эксплуатационные расходы возрастают в среднем на 1,3 тысячи рублей. Другой коэффициент а₀ носит название свободного параметра и отражает постоянную составляющую эксплуатационных расходов, не зависящую от возраста.

Установлением вида статистической связи в виде прямой линии завершается выполнение расчетно-графической работы.
Контрольные вопросы
1. Что такое коэффициент корреляции? В чем его отличие от коэффициента Фехнера?

2. Для чего производится группировка станков по возрастным диапазонам?

3. Дайте характеристику показателю среднего квадратического отклонения.

4. Что такое коэффициент Фехнера?

5. Что такое мода и как она определяется?

6. Статистический смысл медианы.

7. Что такое диаграмма рассеяния и линия регрессии?

8. Объясните экономический смысл коэффициентов уравнения регрессии.

9. Какие средние величины рассчитывались в РГР?
Библиографический список
1. Математические методы в логистике. Задачи и решения / Г.И. Просветов. М.: Альфа-Пресс, 2009. - 303 с.

2. Теория статистики: Учебник/Под ред. Проф. Р.А. Шмойловой. - 3-е изд., перераб. - М.: Финансы и статистика, 2002. - 560 c..

3. Практикум по теории статистики: Учебное пособие /Под ред. Проф. Р.А. Шмойловой. -М.: Финансы и статистика, 2001. - 416 c.

4. Минашкин В.Г., Козарезова Л.О. Основы теории статистики: Учеб. пособие.- М.: Финансы и статистика , 2004.-144с.