Методические указания по дисциплине Фотограмметрия и дешифрирование снимков предназначены для студентов специальности 020501 Картография
 Скачать 453.19 Kb. Скачать 453.19 Kb.
|
OBLPO'г Рис. 5 В ней за начало координат принят центр общеземного эллипсоида О'г, а плоскостью X'г Y'г является плоскость экватора. Ось X'г находится в плоскости начального меридиана, а ось Z'г совмещена с полярной осью О'г Р. Система координат правая. За фигуру Земли принимается эллипсоид вращения с полуосями а и b и сжатием е. Любая точка О пространства задаётся геодезическими координатами: широтой В, долготойL и высотой Н. Геоцентрические координаты X'г,Y'г, Z'г точки О находят по их геодезическим координатам, с помощью известных формул сфероидической геодезии. Может использоваться и прямоугольная система координат X"г Y"г Z"г, представленная на рис.5. Она сохраняет все преимущества геоцентрической системы, но абсолютные значения координат точек в ней меньше. Ось Z"г нормальна к поверхности эллипсоида в начальной точке О картографируемого участка; ось Y"г совпадает с направлением на север. Система координат правая. За начало счёта высот принимается такое значение, при котором аппликаты всех точек положительны. Координаты X"г, Y"г, Z"г, легко получаются из геоцентрических X'г, Y'г, Z'г путём трёхмерного преобразования, включающего перенос начала координат и их вращение. При решении задач на сравнительно небольшом участке местности используется известная левая система прямоугольных координат Zг Zг Z Xг Xг X Yг Yг Y Oг A MS m A'а б Рис.6 Oг Xг Yг Zг (рис.6) Гаусса. На практике часто находит применение местная система пространственных прямоугольных координат Xг Yг Zг с началом в некоторой точке А картографируемого участка (рис.6). В этой системе ось Zг нормальна к поверхности квазигеоида в точке А, ось Xг горизонтальна и параллельна осевому меридиану зоны, в которой находится участок съёмки, а ось Yг направлена на восток. Координаты начала задаются в системе Ог Xг Yг Zг. На каждом снимке по его периметру имеется ряд координатных меток, которые определяют плоскую прямоугольную систему координат o' x y. Такая система при наличии на снимке четырёх меток 1, 2, 3, 4 показана на рис. 7. Начало координат находится в точке о' пересечение отрезков 1-2 и 3-4. Ось x совмещается с прямой 1-2, а ось y с перпендикуляром к оси x в точке о'. Возможны и другие варианты. Например, ось y – это главная вертикаль, а ось x - одна из горизонталей и т. д. Отметим, что на наземных снимках оси обозначают буквами x и z, а координаты в системе координат снимка иногда называют фотокоординатами. Положение точка на снимке определяется координатами x и y, но это можно сделать и в пространственной фотограмметрической системе X'Y'Z' (рис.8). Начало координат этой системы всегда совмещено с точкой фотографирования S, а оси X', Y', Z' параллельны осям X, Y, Z фотограмметрической системы координат точек объекта местности или осям геодезической системы координат. Связи между плоскими и пространственными координатами точек снимка и местности устанавливаются через элементы ориентирования снимка. m y x o' x y Рис.7. Плоская прямоугольная система координат снимка Z' Y' X' X'm Y'm Z'm M S m o Рис.8. Пространственная система координат точки снимка x y Элементами ориентирования снимка называются величины, определяющие его положение в момент фотографирования относительно выбранной пространственной прямоугольной системы координат. Различают элементы внутреннего и внешнего ориентирования снимка. S f y o o' x y0 x0 Рис.9. Элементы внутреннего ориентирования снимка Элементы внутреннего ориентирования позволяют найти положение центра проекции относительно снимка, а значит восстановить связку проектирующих лучей, существовавшую в момент фотографирования. К ним относятся координаты главной точки x0, y0 снимка и фокусное расстояние f фотокамеры (рис.9). Элементы внешнего ориентирования (ЭВО) позволяют установить положение снимка (связки), которое она занимала в момент фотографирования относительно заданной пространственной прямоугольной системы координат. Для снимков, полученных АФА, на практике используют две таких системы. В первую систему ЭВО (рис. 10) входят координаты Xs, Ys, Zs точки фотографирования, а также углы поворота снимка α, ω и κ Продольный угол наклона снимка α образуется осью Z΄ и проекцией главного луча Sо на плоскость X΄ Z΄. Поперечный угол наклона снимка ω заключён между главным лучом Sо и его проекцией на плоскость X΄ Z΄. Угол поворота снимка κ образуют ось у снимка и след плоскости, проходящей через главный луч Sо и ось Y΄ (в этой плоскости находится угол ω). На рис. 10 углы κ и ω положительные, угол α - отрицательный. Вторая система (рис.11) ЭВО содержит: координаты Xs, Ys, Zs точки фотографирования; t – дирекционный угол оптической оси фотокамеры – он образуется следом плоскости главного вертикала W и положительным направлением оси X΄; ε - угол наклона снимка, находится в плоскости главного вертикала между главным и надирным лучами; κ – угол поворота в плоскости снимка, образуется главной вертикалью  и осью y плоской системы координат x y. и осью y плоской системы координат x y.Рис.10 Рис.11 Вопросы для самоконтроля
Тема 2.3 Масштаб аэрофотоснимка Масштабом снимка 1/m в данной точке по данному направлению называется отношение бесконечно малого отрезка dlна снимке к соответствующему отрезку dL на местности. То есть:
dL X Y S dX dY x dx y o dy dl a b Рис 12. a – горизонтальный отрезок на местности, b -его изображение Пусть местность равнинная, а начала координат в пространстве и на снимке расположены соответственно в точках Sиo,(рис. 12). Обозначив проекции отрезков dlиdLна соответствующие координатные оси через dx, dyиdX,dY, с учетом данного определения масштаба и рис. 22 напишем:
где φ – угол между осью x снимка и заданным направлением отрезка dl. При указанном выборе систем координат, и при условии, что оси ординат расположены в плоскости главного вертикала, справедливы формулы зависимости между координатами точек местности и снимка 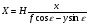 и и 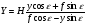 Введём обозначение: 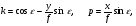 . .После преобразований получим:
Полученное равенство показывает, что масштаб снимка зависит от фокусного расстояния АФА, высоты фотографирования, угла наклона снимка, положения точки на снимке (координат x и y), в которой взят элемент dl и от направления φ этого элемента относительно линии главного вертикала 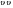 . .Определим значение масштаба 1/m для частных случаев. 1. Масштаб горизонтального снимка (ε = 0): 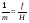 , ,т. е. масштаб горизонтального снимка плоской местности во всех точках постоянный. 2. Масштаб наклонного снимка по направлению главной вертикали (x = 0, φ = 90):
В главной точке снимка o (y = 0) 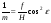 ; ;В точке нулевых искажений с 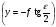 , поэтому: , поэтому: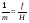 ; ;В точке надира n 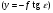 , после подстановки получаем: , после подстановки получаем: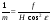 ; ;В главной точке схода 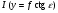  . .3. Масштаб наклонного снимка по направлению горизонтали (φ = 0°)
Поскольку в уравнении абсцисса точки отсутствует, то вдоль горизонтали, если местность равнинная, масштаб величина постоянная. Запишем выражения 1/m для горизонталей, проходящих через характерные точки снимка: По линии действительного горизонта 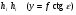 , поэтому: , поэтому: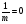 ; ;Вдоль главной горизонтали 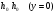 : : ; ;На линии неискажённого масштаба 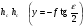 , значит , значит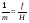 ; ;По горизонтали hnhn, проходящей через точку надира 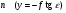 , и: , и: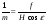 . .Выполненный анализ показал, что масштаб снимка в точке c по любому направлению равен масштабу горизонтального снимка. Вопросы для самоконтроля
Тема 2.4Искажения на аэрофотоснимке Под влиянием угла наклона аэрофотоснимка возникают линейные и угловые искажения изображения на снимке. Зависимость между координатами горизонтального и наклонного снимков можно отметить с помощью строгих и простых соотношений. Их можно написать, если начало координат на снимке и на местности совместить с точкой нулевых искажений с:
Из зависимостей между координатами горизонтального и наклонного снимков можно сделать вывод: 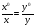 Это означает, что если наклонный снимок совместить с горизонтальным, вращением его вокруг линии неискаженных масштабов (рис. 13.) то соответствующие точки окажутся на одном луче, проходящем через точку нулевых искажений c. с xo yo y x r ro r y x Рис.13 Величина смещений точек за наклон снимка будет равна:
Смещение 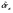 возможно как в сторону точки нулевых искажений, при (0, 180), так и в противоположную сторону. Максимально оно на главной вертикали (φ равно 90° или 270°). На линии неискаженных масштабов точки за наклон не смещаются. возможно как в сторону точки нулевых искажений, при (0, 180), так и в противоположную сторону. Максимально оно на главной вертикали (φ равно 90° или 270°). На линии неискаженных масштабов точки за наклон не смещаются.Величину максимального смещения точек можно оценивать по приближенной формуле:
Оно приводит к ошибкам в определении по снимкам направлений, расстояний и площадей. Рельеф местности также вызывает смещение точек, причем по направлениям проходящим через точку надира n, в которую сходятся изображения отвесных прямых. То есть, если h - превышение точки А над точкой В, расположенной в плоскости предмета, и отрезок АВ отвесный, то точка а на снимке сместится относительно точки b на величину ab = δrh (рис. 14). При h > 0 смещение происходит от точки надира, когда h < 0, – к точке надира. S n N A a b Рис. 14 Смещение за рельеф h |

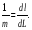
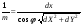 ,
,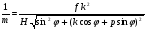 .
. .
.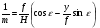
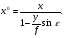 ,
, 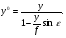
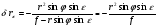 .
.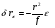 .
.