Контрольная (3). Методические указания по дисциплине Идентификация и диагностика систем к контрольной работе идентификация динамических систем по методу мнк
 Скачать 0.53 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ ИНСТИТУТ ГЕОЛОГИИ И НЕФТЕГАЗОДОБЫЧИ Кафедра «Автоматизации и управления» МЕТОДИЧЕСКИЕ УКАЗАНИЯ по дисциплине «Идентификация и диагностика систем» к контрольной работе «ИДЕНТИФИКАЦИЯ ДИНАМИЧЕСКИХ СИСТЕМ ПО МЕТОДУ МНК» Тюмень 2021 Содержание 1. Обратная задача моделирования. Метод наименьших квадратов 3 2. Приведение модели системы к линейно-регрессионному виду 8 3. Построение алгоритма идентификации и проверка результатов 10 4. Задания к лабораторной работе 14 1. Обратная задача моделирования. Метод наименьших квадратов Рассмотрим динамическую систему, модель которой представляется функциональной зависимостью  , где  - выходной (измеряемый) сигнал,  - входная управляющая переменная,  - совокупность параметров модели.Прямая задача моделирования: пусть сигнал управления задан на некотором интервале времени  , известна функция модели F и определенны ее параметры с. Необходимо определить значение выхода на указанном периоде времени при заданных начальных условиях (н.у.) выходной функции  и ее производных (если потребуется).  Рис. 1 Структурная схема задачи прямого моделирования Обратная задача моделирования (идентификация): известно значение сигнала управления  на интервале времени и известна реакция системы на это управление – т.е. измеренный сигнал переходного процесса на выходе  . Необходимо определить вид функции F (идентификация в большом) или параметры модели с (идентификация в малом). Для идентификации в малом необходимо построить алгоритм 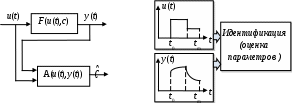 оценивания параметров модели  на основе данных измерений входного и выходного  сигналов модели.  Рис. 2 Структурная схема идентификации Одним из распространенных методов идентификации динамических систем является метод наименьших квадратов (МНК). Рассмотрим динамическую систему, заданную дифференциальным уравнением (иначе - в виде передаточной функции):  (1)(  ,  - коэффициенты,  ,  ) или в виде: где  - оператор производной, Перепишем это уравнение, оставляя в левой части выходной сигнал : иначе:  (2)где введены следующие обозначения: 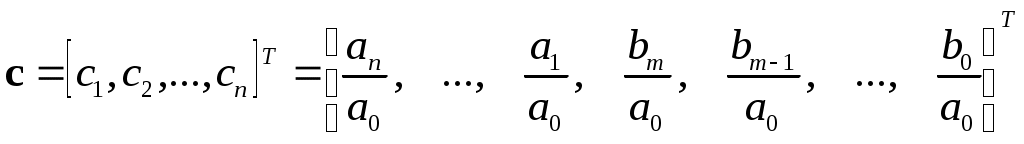 , - вектор параметров,  - вектор регрессионных переменныхПо-сути мы получили модель в виде  , при этом параметры описываются вектором  , а функция  описывает линейную зависимость между параметрами и производными входного и выходного сигналов. Запись модели в виде (2) называется записью в линейно-регрессионном виде.При решении задачи идентификации, параметры модели (1) (и соответственно (2)) являются неизвестными и подлежащими определению. Пусть сигнал 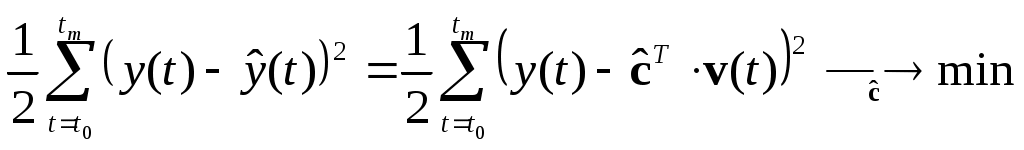 и регрессионные переменные  - доступны к измерению (известны) на периоде  . Будем искать оценку параметров  . Для этого построим оценку выхода модели (2) с использованием оценки параметров  и измеряемых регрессоров  :  . Запишем квадратичное уравнение невязки и будем искать его минимум: Данная запись означает, что минимальное отклонение (по квадратичному критерию) измеряемого выхода от его оценки  для всех значений времени  достигается при точных оценках параметров  .Для поиска минимума критерия находим его производную по вектору 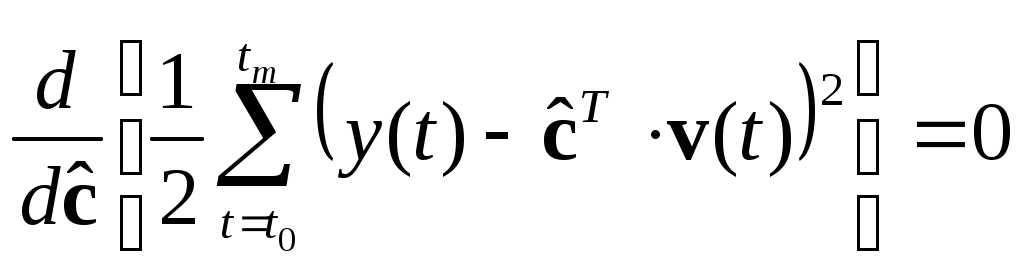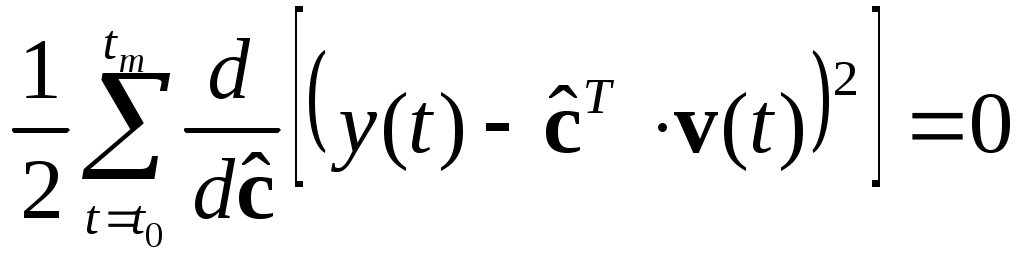и приравниваем его к нулю:  по правилу: 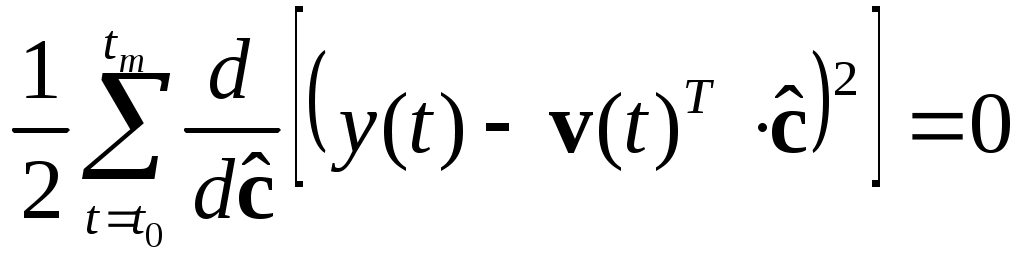  ()отсюда по правилу дифференцирования сложных функций 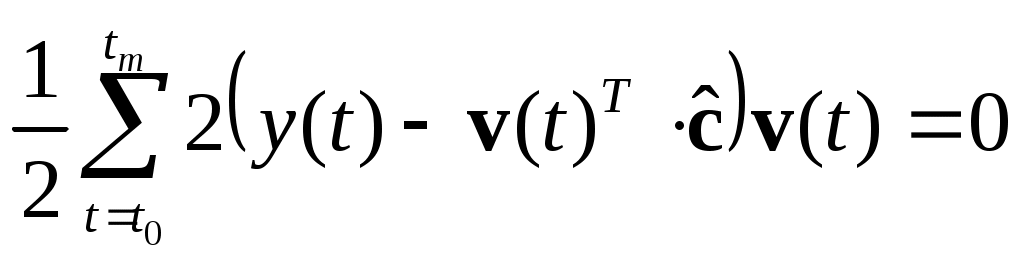 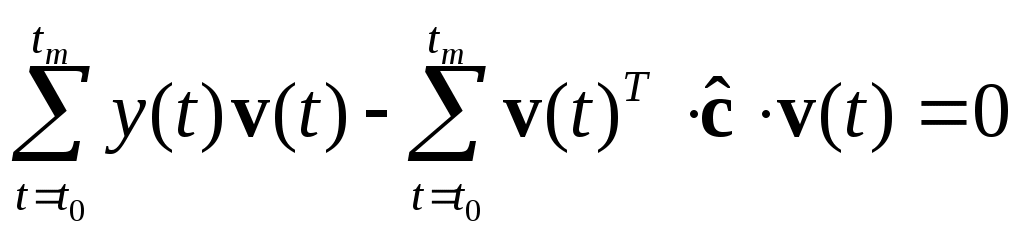:  по правилу: 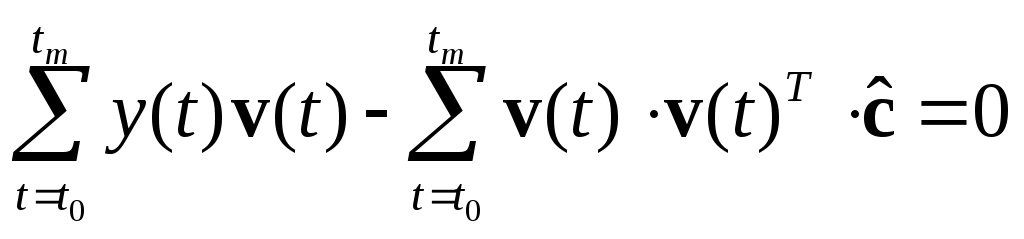  и окончательно: 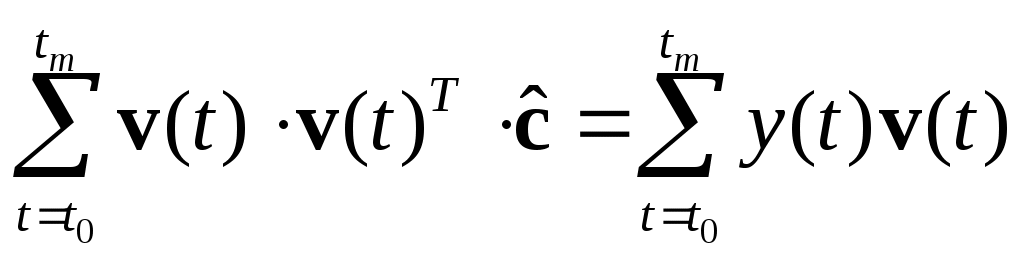 или в матричном виде (т.е. в виде системы линейных алгебраических уравнений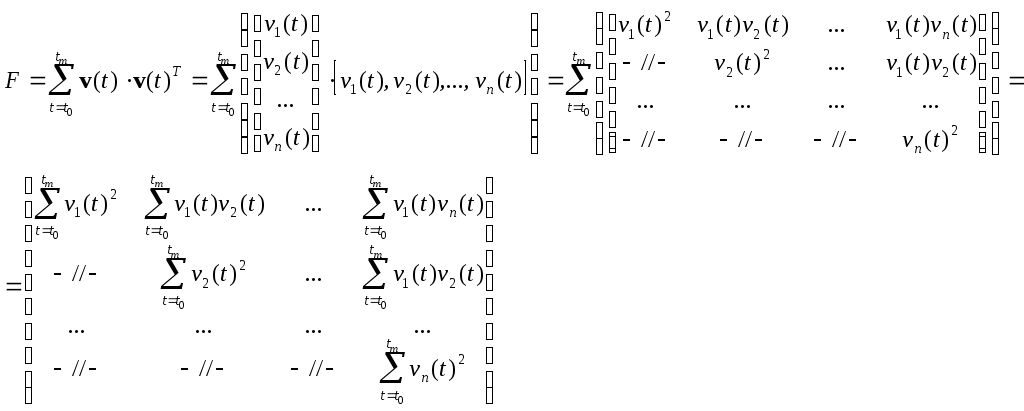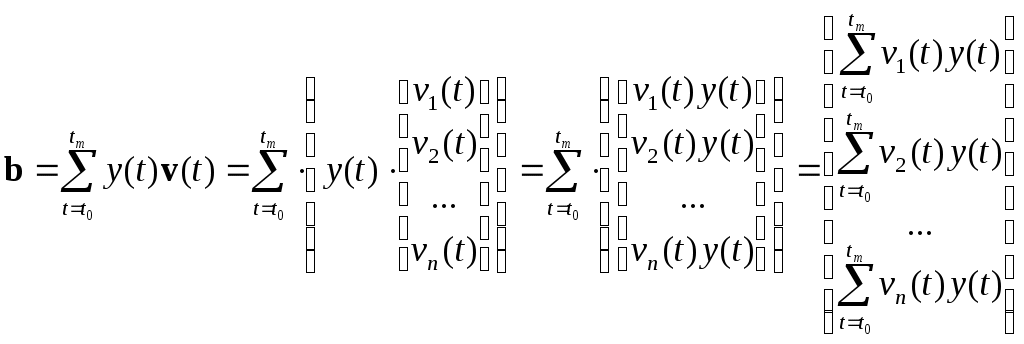):  (3) где  ( означает запись симметричного относительно диагонали элемента). .Тем самым решение задачи идентификации по схеме МНК будет получаться на основе решения системы уравнений (3), которое дает искомые оценки вектора параметров  в виде:  , (4)где  - обратная матрица к .Пример № 1. Пусть динамическая система задана уравнением второго порядка:  или в операторном виде:  Оставляя в левой части переменную , запишем: или в линейно-регрессионном виде (2): 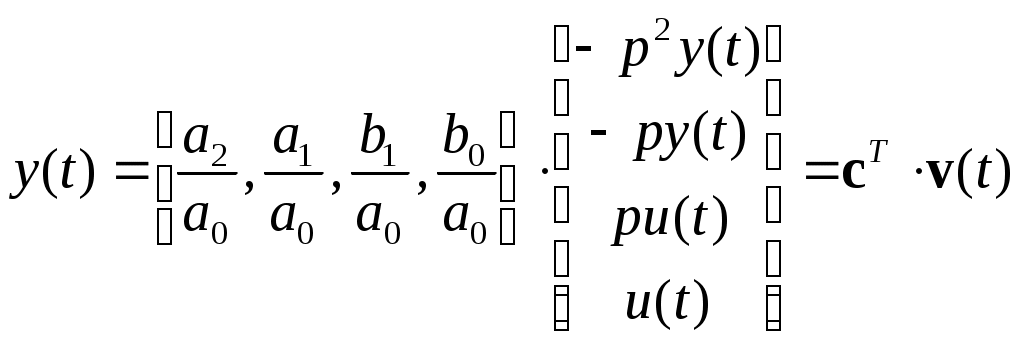 ,Переходя к дискретному времени, получим: 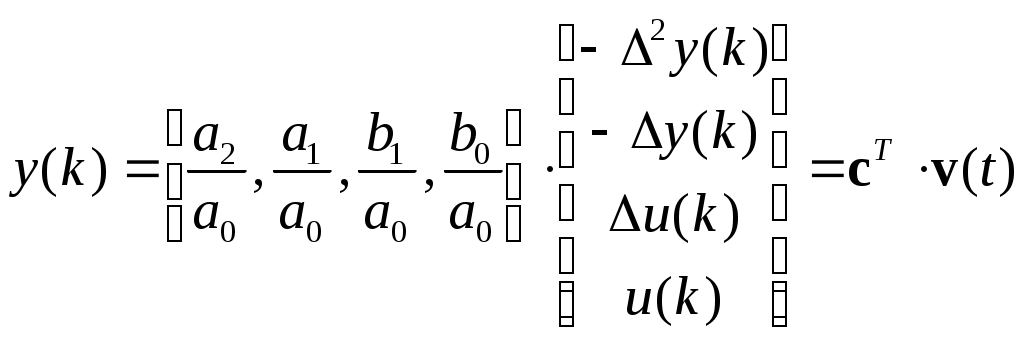 , Решающее уравнение схемы МНК запишется в виде 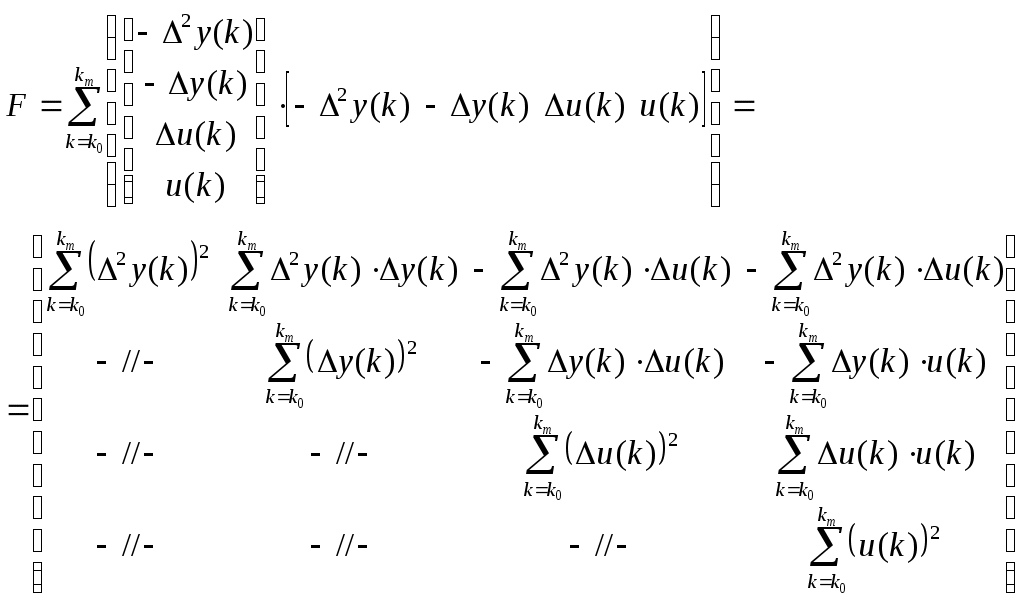 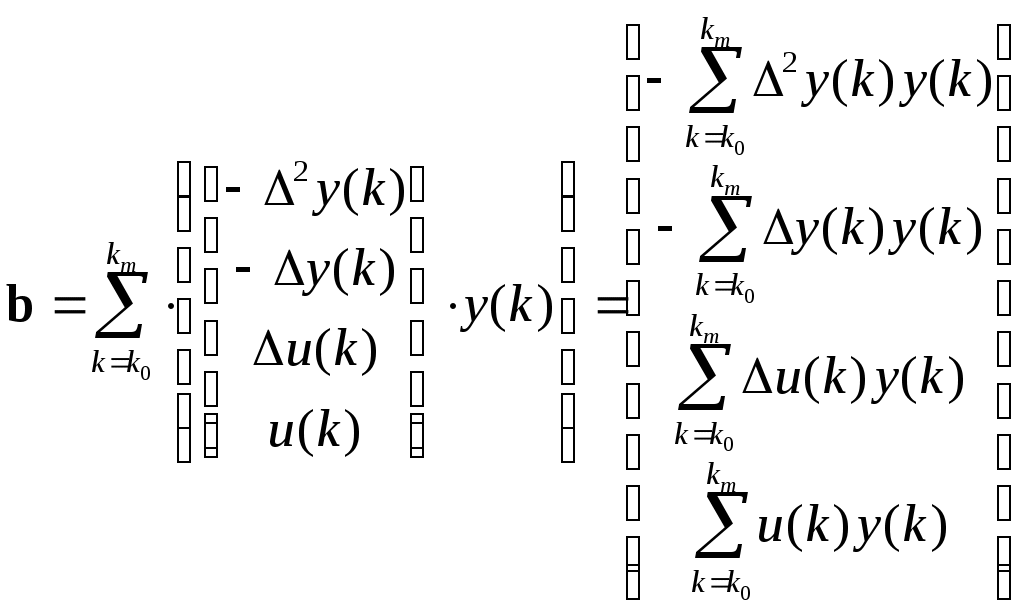,   2. Приведение модели системы к линейно-регрессионному виду Для использования схемы МНК необходимо уравнение модели привести к линейно-регрессионному виду (2):  Необходимо отметить, что такое приведение всегда неоднозначно (может быть получено множеством способов). Отметим некоторые особенности построения схемы МНК: 1) Приведение модели к линейно-регрессионному виду всегда начинается с составления уравнения модели, включающего только измеряемые переменные. В данном уравнении производится группировка относительно переменных, после чего выбирается выходная переменная , и формируется вектор регрессоров в правой части.Пример: в уравнении  После группировки получаем  ; Выбираем в качестве выходной переменную  :  ; Заметим, что в этом уравнении можно сгруппировать два последних слагаемых относительно общего параметра  :  Вектор регрессоров в правой части запишется в виде: 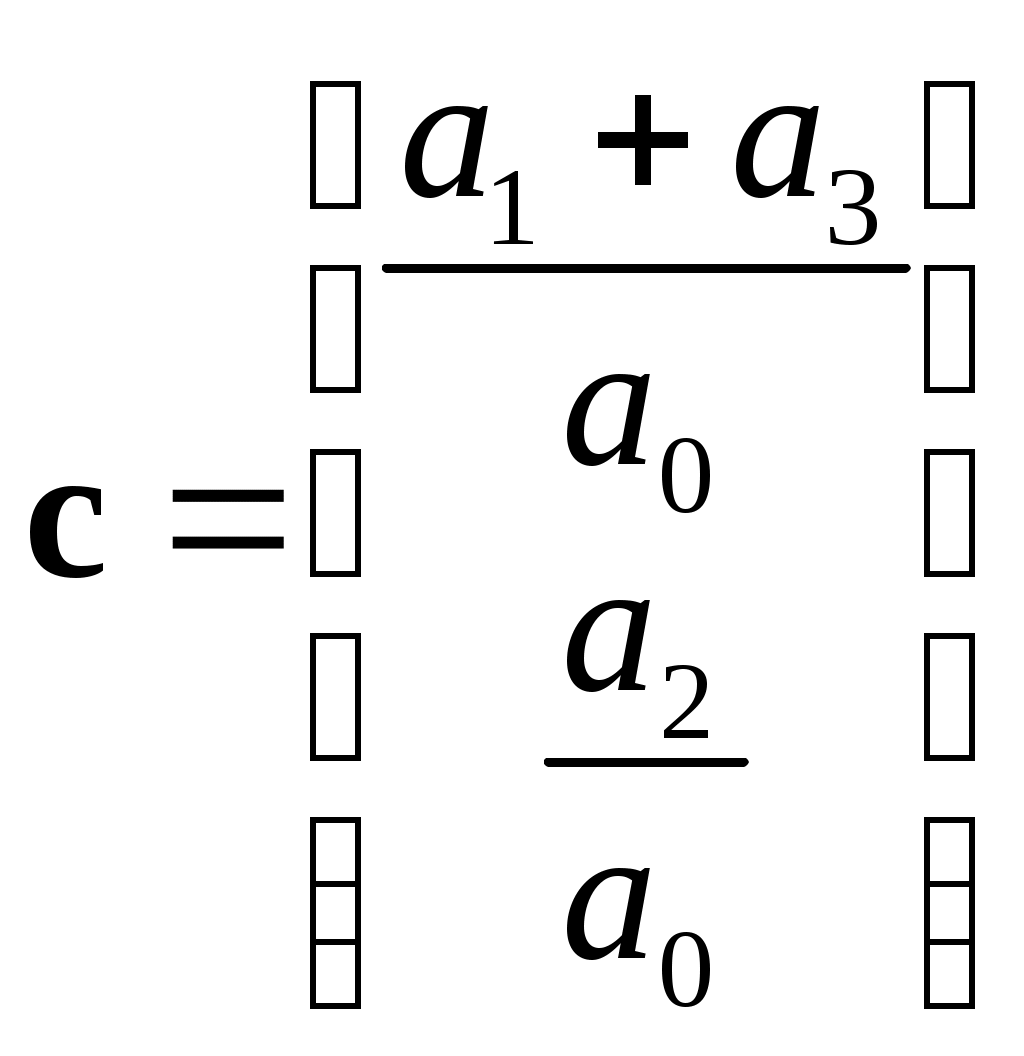 ,  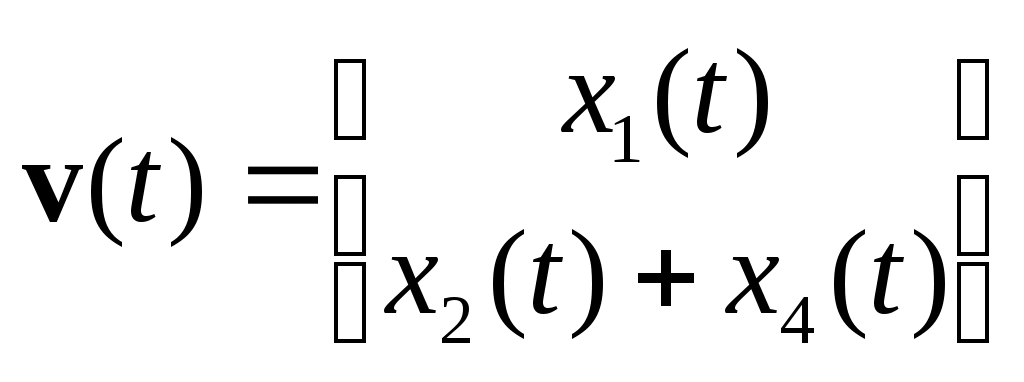,  2) Знаки регрессионных переменных  переносятся в вектор Пример: пусть 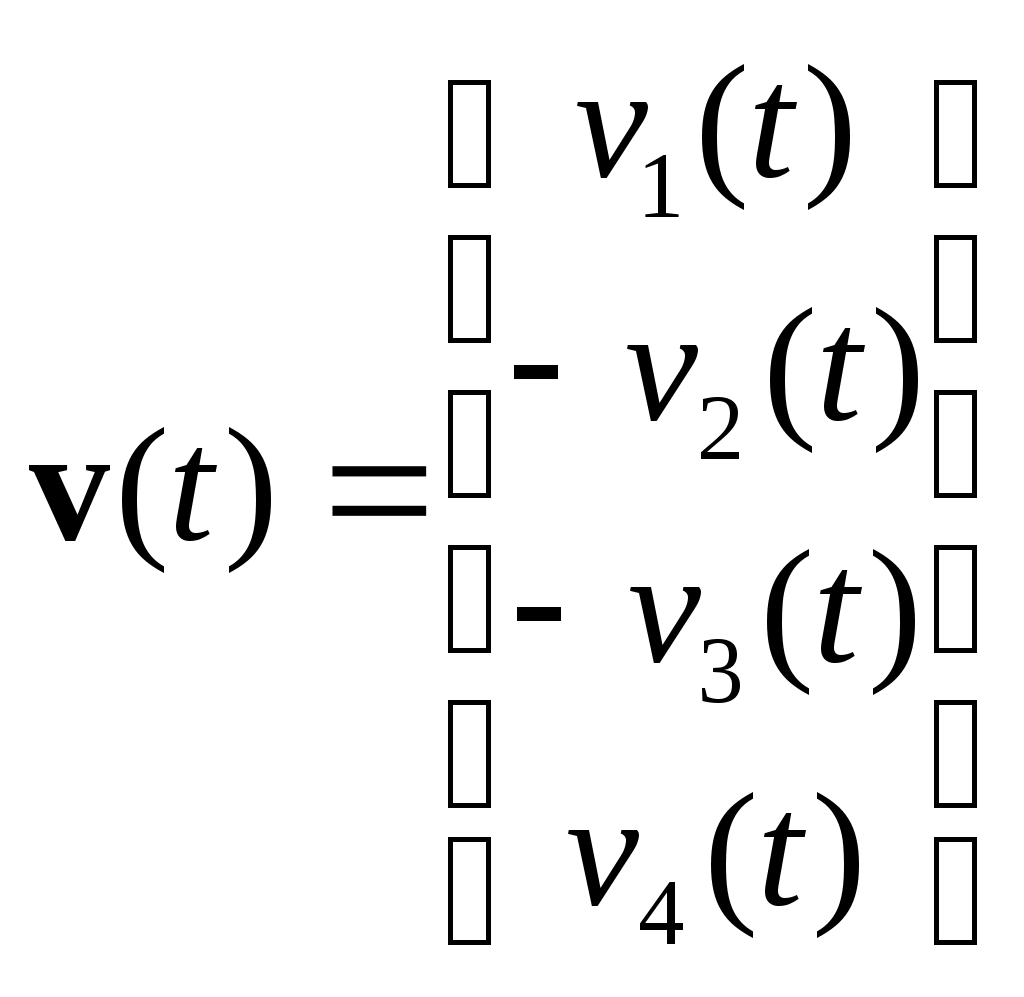 , тогда  .3) В левой части линейно-регрессионного уравнения, в качестве выходной переменной может быть записана любая линейно-независимая переменная (исключая переменные управления  и их производные) из исходного дифференциального уравнения. Пример:  или в операторном виде:  Вариант 1: в качестве выходной переменной берем исходную , тогда  Вариант 2: в качестве выходной переменной берем производную  , тогда  Выбор выходной переменной влияет на вид регрессионного уравнения и может влиять на надежность и точность его работы. 4) Одно из основных условий, обеспечивающих работоспособность схемы МНК-идентификации, является использование данных о динамике процессов при формировании расчетной выборки (матриц и вектора ). Т.е. входное воздействие должно быть таковым, чтобы выходной сигнал и все его производные, входящие в уравнение системы, были «подвижными» - образовывали переходные процессы. Пример:  или в операторном виде:  В качестве выхода берем переменную 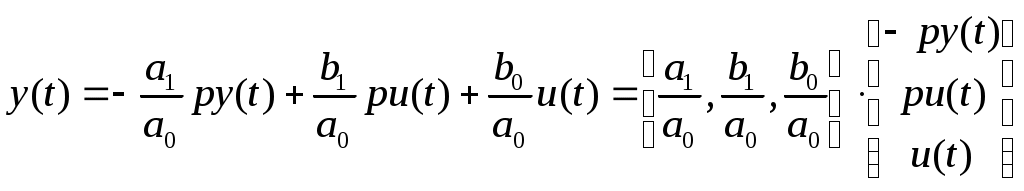, тогда  Вариант 1: пусть  , отсюда  - все регрессионные переменные изменяются со временем («подвижны»).Вариант 2: пусть  , отсюда  - одна из регрессионных переменных «неподвижна», поэтому ее необходимо исключить из регрессионного уравнения: 5) При численном моделировании исходной системы (т.е. в дискретном времени  ), вместо непрерывных регрессионных переменных  и выходной переменной рассматриваются их дискретные аналоги и  . 3. Построение алгоритма идентификации и проверка результатов Для модели в форме передаточной функции (линейного дифференциального уравнения) 1. Моделирование переходного процесса 1) Рассмотрим модель в виде п.ф.:  Зададим временной период  и шаг интегрирования  2) Модель переводится в дискретный вид:  где  - символ оператора дискретного аналога производной (конечная разность), при этом временной интервал разбивается на массив точек  3) Задается сигнал управления  и его производная  4) Уравнение модели записывается в регрессионном виде, принимая за выходную переменную  :   Раскрывая скобки и группируя переменные, получим:  По этому уравнению строится численная схема расчета переходного процесса (выходного сигнала ).2. Идентификация по схеме МНК Для модели в форме передаточной функции (линейного дифференциального уравнения) 1) Еще раз записываем исходное уравнение п.ф. (в дискретной форме): Выбираем переменную, которая будет служить в качестве выходной в схеме МНК:  2) Полученное линейно-регрессионное уравнение записываем в векторном виде: 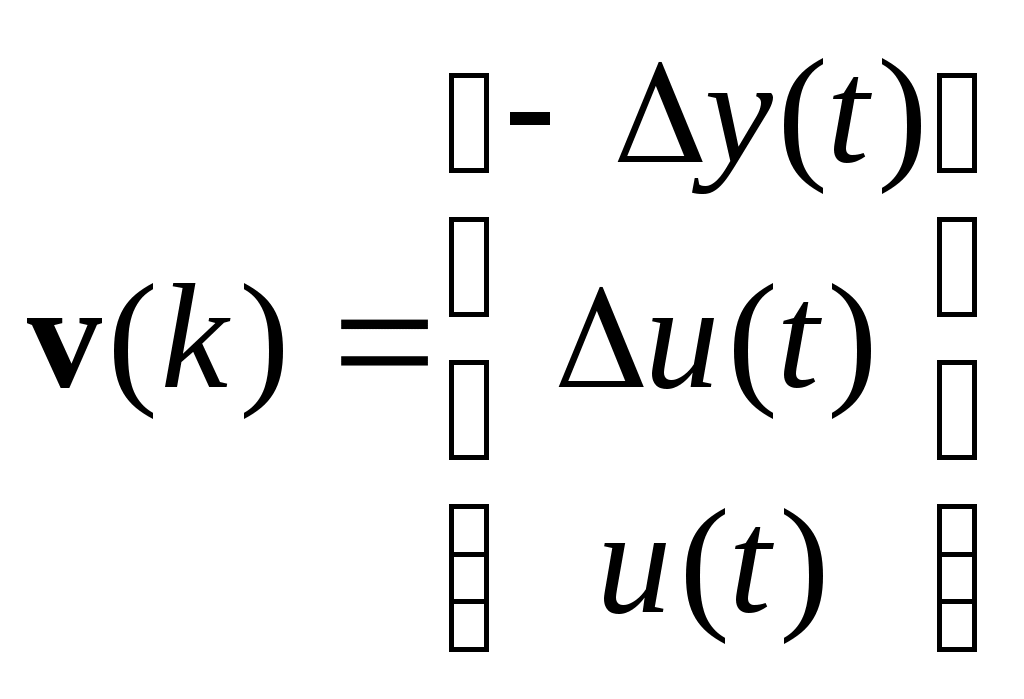 , где - вектор параметров,  - вектор регрессионных переменных.3) Формируем матрицу 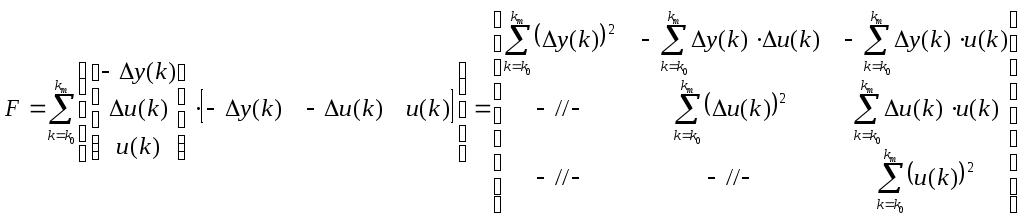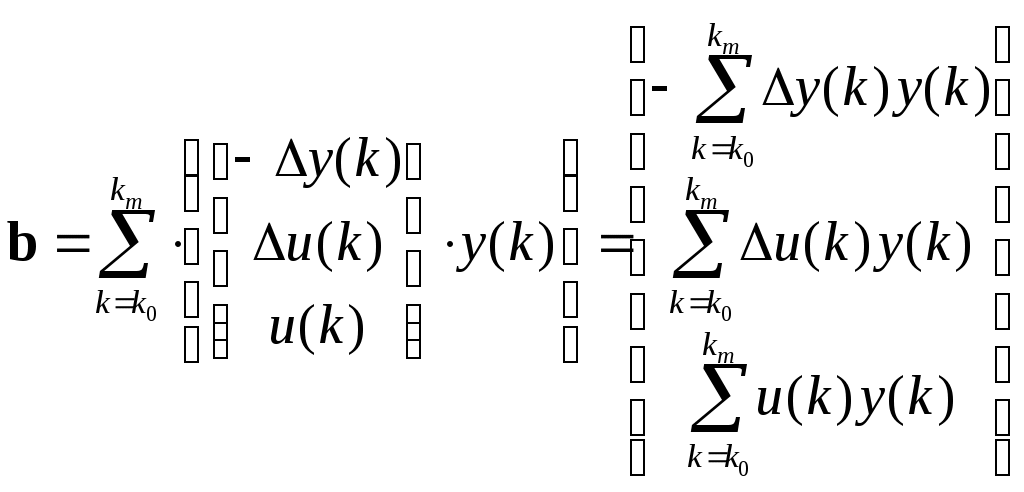и вектор  для схемы МНК:  Находим решение схемы МНК – оценку вектора параметров по уравнению:  Для модели в форме пространства состояний (система из дифференциальных уравнений 1-й степени) 1. Моделирование переходного процесса 1) Рассмотрим модель в форме пространства состояний: 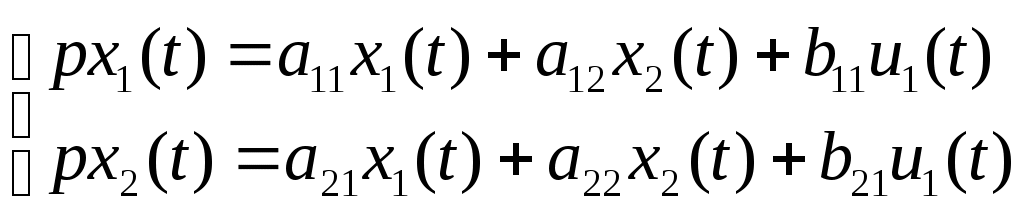 Здесь  - переменные состояния,  - сигналы управления,  и  - параметры модели.Зададим временной период и шаг интегрирования 2) Модель переводится в дискретный вид: 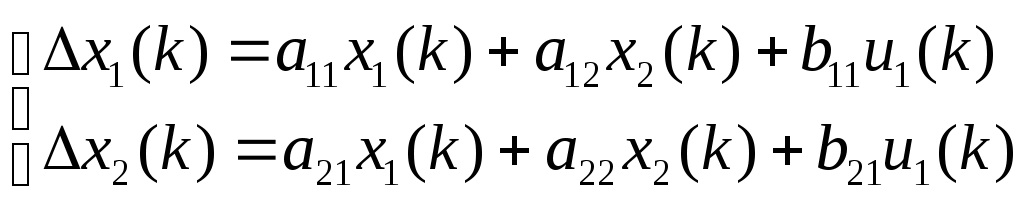 3) Задается сигнал управления и его производная 4) Строится численная схема расчета с использованием схемы Эйлера. 2. Идентификация по схеме МНК 1) Записываем исходную модель (в дискретной форме): 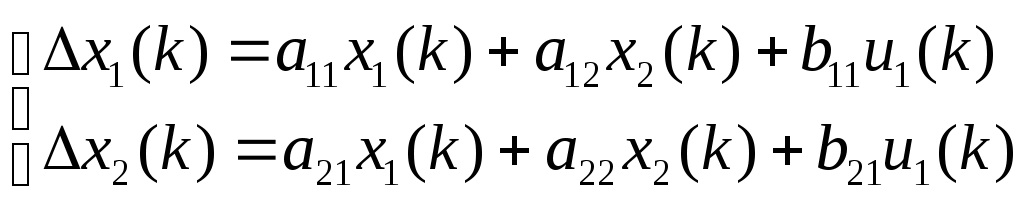Выбирается переменная состояния доступная к измерению, после чего из системы исключается переменная (переменные) недоступная к измерению. Пусть измеряется  , и переменная  не доступна к измерению. Она исключается из системы, для этого из первого уравнения выражается и подставляется во второе:  Раскрываем скобки:  И группируем переменные 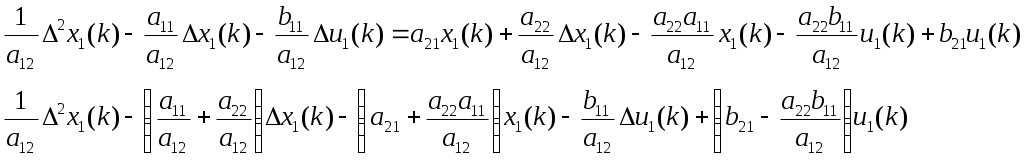 2) В качестве выходной переменной примем сигнал  , переносим его в левую часть: и окончательно (умножая правую часть на коэффициент  ): получим искомую линейно-регрессионную форму 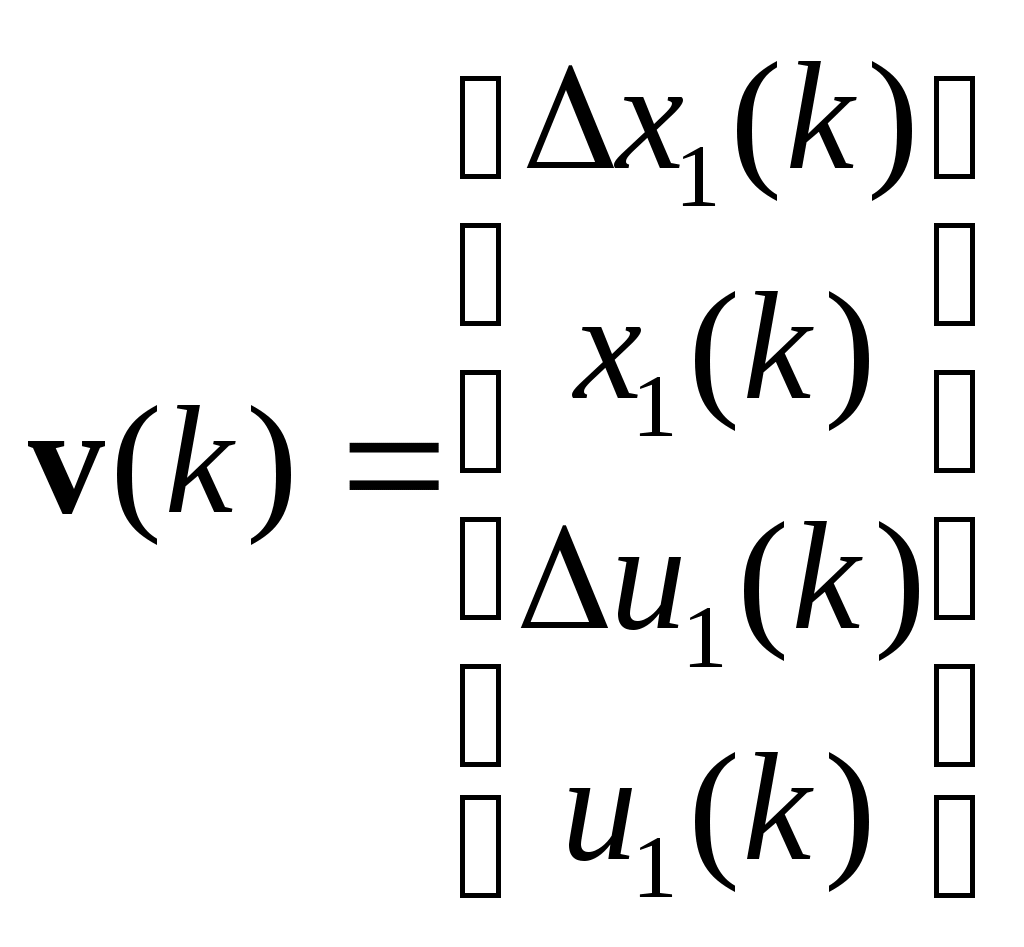 , где  - вектор параметров,  - вектор регрессионных переменных.3) Формируется матрица и вектор для схемы МНК. Находится решение схемы МНК – оценку вектора параметров по уравнению: Проверка результатов идентификации Проверка результатов идентификации возможна двумя способами: 1) Сравнение параметров модели и результатов идентификации Нам заданы параметры модели 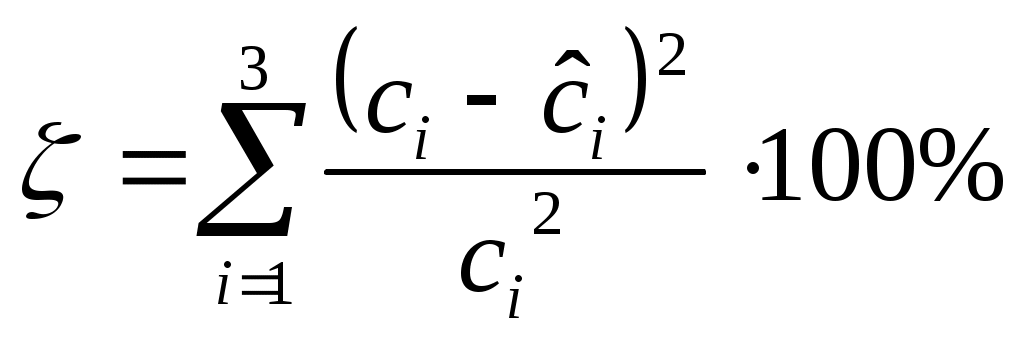 . При составлении линейно-регрессионного уравнения данные параметры образуют вектор . Его можно напрямую сравнить с результатом идентификации – оценкой  . Т.е. каждый элемент вектора сравнивается с соответствующим элементом вектора  . Для получения оценки среднего рассогласования (отличия) результатов такого сравнения можно использовать суммарное среднеквадратическое отклонение (СКО): N.B. В случае если размерность вектора параметров равна количеству параметров модели, то из оценок вектора можно восстановить оценки параметров модели. В нашем случае размерность вектора равна трем, поэтому по его оценке нельзя восстановить четыре параметра модели .2) Сравнение графиков модельного выходного сигнала и оценки выходного сигнала, восстановленной по схеме МНК В качестве исходных данных для схемы МНК нам задан график (переходный процесс) выходного сигнала  . Мы можем построить оценку этого сигнала  , используя найденную оценку вектора параметров по линейно-регрессионной формуле: Сравнить модельный сигнал 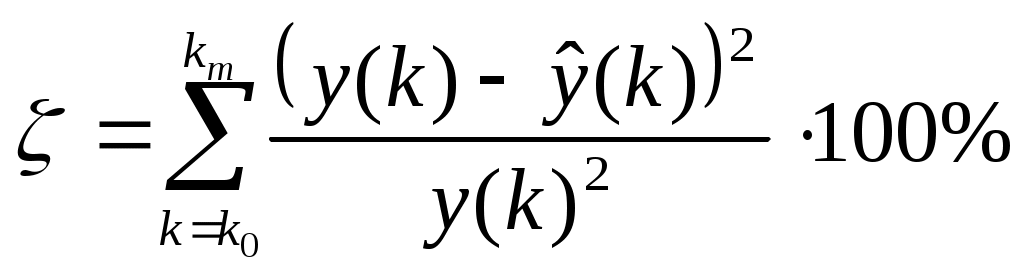и оценку сигнала  можно по формуле для суммы СКО для всех точек измерений: При точных оценках вектора СКО должно равняться нулю и графики и должны совпадать. 4. Задания к контрольной работе Задана система из двух линейных дифференциальных уравнений: 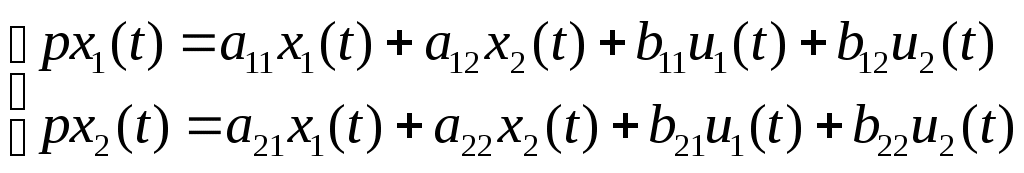 где  ,  - переменные состояния,  и  - входные сигналы,  и - известные параметры. Значения параметров и и выбор переменной состояния доступной к измерению указаны в таблице 1. Параметры моделирования (временной интервал и шаг дискретизации) и форма входных сигналов и указаны в таблице 2.Необходимо схему численного моделирования системы, заданной в виде передаточной функции. Построить графики переходных процессов переменных состояний и графики сигналов управления. Построить схему МНК – идентификации для данной модели, проверить результаты идентификации по параметрам модели и по графикам выбранного выходного сигнала. Таблица 1 Значения параметров системы
Таблица 2. Параметры моделирования и формы сигналов управления
|
