Му контр. р Методология. Методические указания по дисциплине Методология проектирования продуктов питания с заданными свойствами и составом разработаны на кафедре Технология мясных и консервированных продуктов
 Скачать 49.63 Kb. Скачать 49.63 Kb.
|
 Министерство образования и науки Российской Федерации Министерство образования и науки Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Восточно-Сибирский государственный университет технологий и управления» (ФГБОУ ВПО ВСГУТУ) Методические указания к выполнению контрольной работы по дисциплине «Методология проектирования продуктов питания с заданными свойствами и составом» Составитель: Лескова С.Ю. Улан-Удэ Издательство ВСГУТУ 2013 Настоящие методические указания предназначены для выполнения контрольной работы студентами заочного обучения по направлению 260200.68 «Продукты питания животного происхождения». Методические указания по дисциплине «Методология проектирования продуктов питания с заданными свойствами и составом» разработаны на кафедре «Технология мясных и консервированных продуктов» Института пищевой инженерии и биотехнологии на основании основной образовательной программы (ООП), разработанной в соответствии с Федеральным государственным образовательным стандартом высшего профессионального образования по направлению подготовки 260200.68 - «Продукты питания животного происхождения», утвержденным приказом Министерства образования и науки Российской Федерации от 21.12.09 №761. Согласно учебному плану для студентов заочного обучения на изучение дисциплины отводится 144 часа (4ЗЕТ), в том числе лекций-8 час, лабораторных работ 8 час и 128 час – СРС. Содержание
Введение В соответствии с рабочим учебным планом дисциплина изучается на первом году обучения (в 1 блоке). Общая трудоёмкость освоения составляет 4 ЗЕТ. Дисциплина входит в базовую часть профессионального цикла. Содержание дисциплины состоит из нескольких основных модулей: теоретические основы проектирования рецептур пищевых продуктов с заданными свойствами и составом; создание рецептур пищевых продуктов с заданными свойствами и составом (разработка алгоритма) математического моделирования рецептур продуктов питания нового поколения: низкокалорийных, со сбалансированным составом и функциональными свойствами, длительного хранения; методология компьютерного проектирования продуктов питания с заданными свойствами и составом. Основу дисциплины составляют задачи разработки алгоритма рецептуры продуктов с заданными свойствами и составом, методы математического моделирования рецептур продуктов питания. В курсе закрепляются такие общепредметные умения как классификация (методов математического моделирования рецептур продуктов питания), оценивание (анализ результатов расчета и разработка корректирующих мероприятий). Основные методы и технологии обучения, применяемые при преподавании данной дисциплины, обеспечивают формирование у студентов общекультурных и профессиональных компетенций, предусмотренных ФГОС ВПО по данному направлению. Для формирования общекультурных и профессиональных компетенций необходимы базовые компетенции, сформированные при изучении следующих учебных дисциплин: - Проектирование комбинированных продуктов питания; - Оптимизация ассортимента и рецептур продуктов животного происхождения. Самостоятельная работа студентов направлена на глубокое и прочное усвоение учебного материала, на развитие способности творческого мышления. Самостоятельная работа студентов по курсу «Методология проектирования продуктов питания с заданными свойствами и составом» предусматривает выполнение контрольной работы.
Методологические подходы к проектированию рецептур многокомпонентных пищевых продуктов Многие страны мира (США, ФРГ, Швеция, Финляндия, Россия и др.) применяют технологии производства продуктов с заданным химическим составом (по белку, жиру, влаге и т.д.), а также технологии проектирования состава многокомпонентных пищевых смесей. Производство продуктов заданного состава требует разработки соответствующего математического обеспечения и использования высокопроизводительного оборудования. Так, применение ЭВМ для расчета рецептур и оптимизации производства продуктов позволяет обеспечить обоснованное количество сырьевых ингредиентов в составе рецептур пищевых продуктов. Одним из основных научных направлений современных биотехнологий является моделирование как инструмент изучения поведения объекта с помощью его математического описания, в частности моделирование технологий составления и прогнозирования функционально-технологических свойств рецептурных смесей пищевых продуктов. Все большее внимание уделяется информационному обеспечению процессов моделирования: методологии, методам, алгоритмам решения конкретных задач и их программной реализации. Математическое моделирование используется при разработке различных рецептур продуктов. Так, при разработке оптимальных рецептур сухих завтраков повышенной биологической ценности применяется методология экспериментально-статистического моделирования (ЭСМ), класс задач «технология – система». Методология основывается на выделении ключевого нутриента моделирования и оптимизации его качества. Это направление получило развитие в ряде аналитических методов расчета качества белковой составляющей отдельных пищевых продуктов и многокомпонентных композиций. Выбор плана эксперимента осуществляется по каталогу последовательно генерированных оптимальных планов для полных полиномов второго порядка. Критерием оптимизации служит содержание каждой из восьми незаменимых аминокислот. Вычислительный эксперимент состоит в получении поверхности отклика по модели при варьировании значений переменных по всему фактору пространства. Локальная область факторного пространства определяется с учетом химического состава сырья. Расчет коэффициентов и статистическая обработка результатов выполняются с помощью регрессионного анализа по методу наименьших квадратов после реализации эксперимента и позволяют получить регрессионные уравнения, адекватно описывающие количество каждой из незаменимых аминокислот при варьировании рецептурного состава продукта. Графическая интерпретация результатов вычислений в виде изолиний на поверхности треугольника по каждой математической модели позволяет на практике прогнозировать количество каждой аминокислоты при выбранном соотношении рецептурных компонентов. При оптимизации рецептур мясных продуктов известно использование симплекс-метода, который является аналитическим методом решения задачи линейного программирования, позволяющим найти оптимальное решение в смысле максимизации или минимизации целевой функции. Процесс принятия решения симплекс-методом переходит из неформализованного к формализованному методу. Принятие формализованных решений базируется на двух основных методах: логическом моделировании и оптимизации. Принятие оптимальных решений основывается на трех составляющих: математической модели, решении задач на компьютере и исходных данных. Оптимизационная задача решает по выбранным показателям (например, химическому составу, витаминному, минеральному составу и энергетической ценности). Для расчета математической модели рецептур мясопродуктов используют исходную выходную информацию. Вся математическая модель состоит из трех составляющих: целевой функции, ограничений и граничных условий. Модель включает в себя: ограничения по содержанию нутриентов, разработку математической модели, результат решения. Данная схема математической модели была использованиа при составлении моделей для конкретных видов мясопродуктов: сарделек с папаратником с морской капустой, пельменей, котлет с облепиховой мукой и пюре из шиповника и боярышника. Н.Н. Липатовым в 1995-2001 гг. проводились исследования по вопросам компьтерного проектирования продуктов и рационов питания с задаваемой пищевой ценностью. Начальная стадия разработки теоретических основ и конкретных методов реализации принципов проектирования сбалансированных пищевых продуктов была связана с формализацией качественных и количественных представлений о рациональности использования незаменимых аминокислот в технологии адекватной экзотрофии. Формализация учитывает взаимосбалансированность незаменимых аминокислот. На основании принципа Митчелла-Блока предложены: коэффициент утилизации j-й незаменимой аминокислоты; коэффициент утилитарности аминокислотного состава в продукте г/100 г белка; коэффициент аминокислотного состава, численно характеризующий сбалансированность незаменимых аминокислот по отношению к физиологически необходимой норме (эталону); показатель сопоставимой избыточности содержания незаменимых аминокислот, характеризующий суммарную массу незаменимых аминокислот, которые не используются на анаболитические цели. Второй стадией создания теоретических и практических основ проектирования пищевых продуктов считается разработка методов моделирования влияния набора и соотношения рецептурных ингредиентов на изменение массовых долей макро-и микропитательных веществ. Методика проектирования рецептур многокомпонентных пищевых продуктов включает в себя три этапа: 1 этап – моделирование аминокислотного состава белка проектируемого пищевого продукта и выбор значений, в наибольшей степени удовлетворяющих критерию; 2 этап – оценка жирнокислотного состава проектируемого продукта; 3 этап – расчет энергетической ценности проектируемых продуктов питания. Методика состава продуктов может быть использована для обоснования сбалансированных пищевых рационов, включающих первые и вторые блюда (с учетом состава гарниров, количества съедаемого хлеба), десертные блюда и напитки. Наиболее перспективно применять данную методику к мясным продуктам, входящим в пищевые рационы определенных групп людей, объединенных по возрастному, профессиональному или другим признакам, питание которых осуществляется централизованно. С.Б.Юдина (1999) при разработке теоретических предпосылок компьютерного проектирования продуктов питания на мясной основе для людей пожилого и престарелого возраста использовала оптимизацию параметров разрабатываемого продукта путем моделирования рецептуры с привлечением интегрального критерия сбалансированности по широкому кругу показателей. При этом применялась квалиметрическая мультипликативная модель, позволяющая свести в одну форму относительные комплексные и простые единичные показатели качества различного характера, обеспечивающие независимость свойств каждого из показателей. Процесс моделирования на ЭВМ, модифицированный автором, осуществлялся в общем виде циклическим алгоритмом Н.Н. Липатова. Для нахождения частного критерия используется функция желательности Харрингтона. Фактор моделирования преобразуется в безразмерную величину, которая выступает показателем соответствия его значения эталону. Преимущество функции желательности Харрингтона заключается в ее безразмерности, что позволяет производить моделирование с использованием факторов различной размерности и диапазона значений, гибкости программирования функции с учетом разброса величины фактора. Ю.А. Ивашкин и соавт. (2001) при разработке экспертной системы адекватного питания при проектировании продуктов предлагают использовать оптимизацию по каждому выбранному критерию с попарным сравнением и оценкой качества полученного продукта по независимому функционалу качества и шкалам желательности. На основе имеющегося опыта по методологии и методам математического моделирования в области пищевых технологий выделяют семь последовательных стадий методологии математического моделирования сложной технологической системы: первая стадия (наиболее важная) – постановка задачи; вторая стадия – определение фундаментальных законов, которым подчиняется механизм явлений составляющих проблему; третья стадия – на основе выбранной физической модели, приминительно к решаемой задаче, записывается система соответствующих математических уравнений; четвертая стадия – при составленных уравнениях определяется метод решения их совместной системы; пятая стадия – выбор одного из нескольких возможных способов решения в зависимости от уровня проведенного исследования процесса и от сложности уравнений модели; седьмая стадия – изучение и подтверждение результатов, полученных при решении математической модели. В последнее время задачи, связанные с моделированием многокомпонентных рецептурных смесей пищевых продуктов, решают с помощью математического программирования количественного состава – заданных парциальных частей (компонентов), входящих в данную смесь. Используемые правила описания систем, состоящих из заданных компонентов смесей, основываются, как правило, на линейных аддитивных моделях, когда их результирующие физические, химические и другие (в том числе потребительские) свойства являются аддитивной (взвешенной) суммой соответствующих свойств компонентов. Задача заключается в отыскании весовых коэффициентов и масс компонентов смеси. При моделировании систем применяется также подход, состоящий в том, что многокомпонентные рецептурные смеси описываются различными регрессионными уравнениями, связывающими характеристики этих смесей с характеристиками и массовыми долями их парциальных компонентов. В основном для этих целей используют полиномиальные зависимости функционально-технологических свойств (ФТС) от массовых долей их парциальных компонентов второго (а иногда, но гораздо реже, третьего) порядка, обосновывая выбор порядка соображениями минимизации наименьших квадратичных ошибок моделей (МНК – метод). Однако полиномиальные зависимости ФТС не всегда согласуются с физическим смыслом задачи, что заставляет находить новые приемы для решения поставленной проблемы. Оптимизация параметров смеси позволяет обеспечить получение (с большей долей вероятности) продуктов заданного качества. Вместе с тем информация о разработке рецептур с учетом взаимодействия компонентов на основе принципов термодинамики в литературных источниках не встречается. В связи с этим создание новых подходов, методологии и моделирования многокомпонентных рецептурных смесей в условиях информационной неопределенности и с учетом взаимодействия компонентов является задачей, решение которой будет способствовать повышению качества пищевых, в том числе мясных продуктов. Моделирование рецептурных смесей пищевых продуктов общего и функционального назначения имеет широкое применение. Оптимизационные задачи решаются по выбранным направлениям, например химическому, минеральному, витаминному составам, энергетической ценности. Большое внимание при этом уделяется вопросам проектиролвания комбинированных мясных продуктов, под которыми понимается процесс создания рациональных рецептур и / или структурных свойств, обеспечивающих задаваемый уровень адекватности. Необходимость получения продуктов с заданным составом по всем макро- и микронутриентам, с определенными физико-химическими характеристиками требует применения технологических решений, отличающихся от традиционных пищевых технологий. Постановка задачи. Любую технологическую систему можно представить некоторым математическим описанием ее функционирования, что является упрощенным отображением наиболее существенных свойств реальной системы. Математическое описание характеризует правило преобразования входных сигналов в выходные при заданной структуре технологии. В основе изучения функционирования технологических систем и процессов всегда лежит эксперимент – реальный или модельный. Суть реального эксперимента – это изучение свойств непосредственно на самом объекте. Модельный эксперимент заключается в изучении поведения объекта с помощью его модели. В данном случае описываются построенная с учетом равновесной термодинамики математическая модель многокомпонентной смеси и созданный на ее основе способ оптимизации рецептурной смеси. При математическом моделировании были использованы программные материалы, разработанные совместно с кафедрой информационных технологий Московского государственного университета технологий и управления под руководством доктора физико-математических наук, профессора А.Е. Краснова. Под оптимизацией многокомпонентной смеси понимают нахождение массовых долей компонентов, которые дают требуемые значения физико-химических, реологических и других (оптических, органолептических) свойств (характеристик) смеси. Чтобы решить задачу составления многокомпонентной смеси, необходимо найти зависимости как между характеристиками системы и ее компонентами, так и между характеристиками системы и массовыми долями ее компонентов. Пусть Xk1 – k-я характеристика l-го компонента (1=1,2, …, K); а М1 – массовая доля l-го компонента (∑ М1 =1; М1 ≥0). Тогда k-я характеристика смеси может быть записана в виде: Fk = ƒk ({M1}, {Xkl}, {Рkl}), (1) где ƒk ({M1}, {Xkl}, {Рkl}) – неизвестная функциональная зависимость с параметрами Рkl , описывающая k-ю характеристику смеси. При введении ограничений на характеристики смеси, которые устанавливаются экспериментально или по соответствующей нормативной документации: F*k –min и F**k –max и задании условий неопределенности в виде аддитивных возмущений (помех): ƒk → ƒk + δƒk, Хkl + δХkl , Рkl → Рkl+ δРkl, Ц({М1}) → Ц + δЦ (Ц ({М1})) целевой критерий, зависящий от совокупности {М1} массовых долей компонентов, получается задача математического программирования рецептурных смесей пищевых продуктов в условиях неопределенности. Модель характеристик многокомпонентных смесей примет вид: Fk = ƒk ({M1}, {Xkl}, {Рkl}) + Нk, (2) где 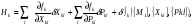 (3) (3)общая помеха (обусловленная как неидеальностью модели, ошибкой эксперимента, так и случайными отклонениями характеристик Xkl от стандартных значений), а ƒk ({M1}, {Xkl}, {Рkl}) возмущение, связанное с взаимодействием компонентов. В этом случае модель оптимизации смеси (например, пищевой) может быть записана в виде задачи математического программирования с неопределенными ограничениями и неопределенным целевым критерием: ƒk ({M1}, {Xkl}, {Рkl}) ≥ Fk* -Hk; k=1, 2, …, К; 1=1, 2, …, L; ƒk ({M1}, {Xkl}, {Рkl}) ≥ Fk** -Hk; Ц({М1}) + δЦ →max (min); ∑ М1 =1; М1 ≥ 0. (4) Выбор модели и составляет основную методологическую проблему математического моделирования оптимизации многокомпонентных смесей. Другой проблемой является обоснование модели зависимостей характеристик смесей и готовых продуктов после теплового, компрессионного или иных видов воздействий. В результате совместной (с преподавателем) и индивидуальной (самостоятельной) деятельности в процессе изучения дисциплины студент-магистр будет демонстрировать следующее: по Разделу 1 (модуль 1) Теоретические и практические основы проектирования рецептур пищевых продуктов с заданными свойствами и составом. на уровне знаний:
на уровне понимания:
на уровне применения:
на уровне анализа:
на уровне синтеза:
на уровне оценки:
по Разделу 2 (модуль 2) «Создание рецептур пищевых продуктов с заданными свойствами и составом». на уровне знаний:
на уровне понимания:
на уровне применения:
на уровне анализа:
на уровне синтеза:
на уровне оценки:
по Разделу 3 (модуль 3) «Методология компьютерного проектирования продуктов питания с заданными свойствами и составом». на уровне знаний:
на уровне понимания:
на уровне применения:
на уровне анализа:
на уровне синтеза:
на уровне оценки:
контрольной работы Контрольная работа – форма самостоятельной работы, на правленной на детальное знакомство с какой-либо темой в рамках данной учебной дисциплины. Основная задача выполнения кон трольной работы по предмету это углубленное изучение определен ной проблемы курса, получение более полной информации по ка кому-либо его разделу. При выполнении контрольной работы необходимо использование достаточного для раскрытия темы количества источников, непосредственно относящихся к изучаемой теме (книг и статей). Можно использовать литературу, рекомендуемую преподавателем, или самостоятельно подобранные источники, а также учебники, желательно использовать не менее четырех источников. При выполнении контрольной работы студент должен усвоить следующие основные умения: - самостоятельный поиск информации по заданной теме; - отбор существенной информации, необходимой для полного освещения изучаемой проблемы, отделение этой информации от второстепенной (в рамках данной темы); - анализ и синтез знаний и исследований по проблеме; - обобщение и классификация информации по исследовательским проблемам; - логичное и последовательное раскрытие темы; - обобщение знаний по проблеме и формулирование выводов из литературного обзора материала; - грамотное построение научного реферативного текста. Требования к оформлению контрольной работы: Основные структурные элементы контрольной работы:
Объем всей контрольной работы (включая титульный лист, содержание, список литературы) должен быть приблизительно равен 10 - 12 страницам. Страницы работы нумеруются в правом верхнем углу, начиная с содержания (с цифры 2). Первоисточник приводимых в тексте цитат указывается в списке литературы с указанием автора, названия работы, издательства, года издания и номера страницы. При изучении дисциплины «Методология проектирования продуктов питания с заданными свойствами и составом» студентами заочной формы обучения выполняется одна контрольная работа. При выполнении контрольной работы студент должен кратко, но в тоже время исчерпывающе, ответить на поставленные вопросы. В ответах следует отказаться от сплошного переписывания текста учебников. Контрольная работа выполняется студентами согласно своего шифра: последняя цифра зачетной книжки студента соответствуют номеру варианта контрольной работы (см. таблицу1).
Таблица 1- Задания по контрольной работе
6. Алгоритм разработки рецептурной смеси продуктов питания с учетом взаимодействия компонентов 7. Прогнозирование рецептур и технологий при разработке продуктов питания заданного химического состава 8. Показатели комплексной оценки качества продуктов питания с заданными составом и свойствами 9.Физиологические нормы потребления основных пищевых веществ 10. Медико-биологические требования, предъявляемые к продуктам питания 11. Принципы построения математических моделей рецептур пищевых продуктов нового поколения 12. Рекомендации к проектированию рецептурного состава мясопродуктов (молочных продуктов) 13. Этапы моделирования рецептурного состава мясопродуктов (молочных продуктов) 14. Критерии медико-биологических требований при проектирование продуктов питания 15. Виды математических моделей 16. Выбор критерия оптимальности, его обоснование 17.Основные ограничения математических моделей рецептурного состава мясопродуктов (молочных продуктов) 18. Алгоритм симплексного метода решения задач линейного программирования 19. Математическая формализация математических моделей рецептурного состава мясопродуктов (молочных продуктов) 20. Алгоритм моделирования рецептуры продукта по пищевой ценности 21. Методика проектирования рецептур продуктов питания с заданными потребительскими свойствами 22. Основные стадии методологии математического моделирования сложной технологической системы 23. Применение оптимизационных задач в промышленности (мясной, молочной) 24. Последовательность поиска оптимальных комбинаций компонентов рецептурного состава продуктов питания. 4. Рекомендуемая литература Таблица 2- Рекомендуемая литература
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
