Математика контрольная работа. Методические указания по оформлению контрольной работы по математике
 Скачать 1.18 Mb. Скачать 1.18 Mb.
|
|
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ по оформлению контрольной работы по математике Контрольная работа должна быть аккуратно оформлена, написана четко и ясно и иметь поля для замечаний рецензента. Каждую контрольную работу следует выполнять в отдельной тетради ручкой. Работа должна быть написана собственноручно. На проверку не допускаются работы распечатанные на принтере или другой множительной технике. Студент выполняет те задачи, последняя цифра номера которых совпадает с последней цифрой его учебного шифра. Например, студент, учебный шифр которого имеет последнюю цифру 0, в контрольной работе №1 решает задачи 1.1.10, 2.1.20, 2.2.20, 3.3.40, 3.1.50; в контрольной работе №2 – 6.2.40, 6.3.20, 7.1.10, 7.2.60, 7.3.30; в контрольной работе №3 – 8.1.10, 8.2.40, 9.1.20, 9.1.60, 10.1.10. Каждая контрольная работа выполняется в отдельной тетради, на обложке которой должны быть указаны: дисциплина, номер контрольной работы, шифр студента, курс, фамилия, имя и отчество студента. На обложке вверху справа указывается фамилия и инициалы преподавателя-рецензента. В конце работы студент ставит свою подпись и дату выполнения работы. В каждой задаче надо полностью выписать ее условие. В том случае, когда несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера. Решение каждой задачи должно содержать подробные вычисления, пояснения, ответ, а также, в случае необходимости, и рисунки. После каждой задачи следует оставлять место для замечаний преподавателя-рецензента. В случае невыполнения этих требований преподаватель возвращает работу для доработки без ее проверки!!! ВАЖНО!!! Если контрольная работа не зачтена. Доработка контрольной работы по гарантии БЕСПЛАТНО! Срок на внесение дополнений и исправлений от 2 суток. Во время сессии сроки на внесение дополнений могут быть выше. По этой причине НЕ ДОЖИДАЙТЕСЬ, когда результаты проверки контрольной вам объявят на занятиях, а САМОСТОЯТЕЛЬНО ЗАРАНЕЕ узнавайте результаты проверки у вашего преподавателя. Работы, которые были сданы на проверку в печатном виде и не переписаны в тетрадь – на доработку не принимаются!!! Для исправления работы от вас нужны фотографии из вашей тетрадки, где видны замечания преподавателя. Исправленную работу необходимо представить на проверку повторно вместе с незачтённой работой. Исправления следует выполнять в конце работы, после рецензии преподавателя, а не в тексте. КОНТРОЛЬНАЯ РАБОТА № 1 Элементы векторной алгебры, аналитической геометрии и линейной алгебры 1.1.1. Найти косинус угла между векторами 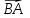 и и 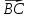 , если А(3;-2;3); В(2;0;1), С(-2;3;1). Сделать чертеж. , если А(3;-2;3); В(2;0;1), С(-2;3;1). Сделать чертеж.Решение: Вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой: AB = {Bx - Ax ; By - Ay ; Bz - Az} Если вектор задан своими координатами: Найдем векторы 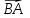 и и 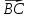 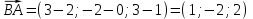 и 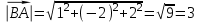 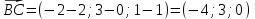 и 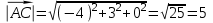 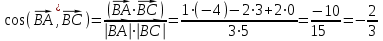 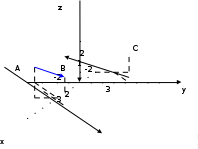 Ответ: 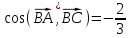 2.1.11 Уравнение одной из сторон квадрата х+3у-5=0. Составить уравнения трех остальных сторон квадрата, если Р(-1;0) - точка пересечения его диагоналей. Сделать чертеж. Решение: Пусть сторона AB квадрата ABCD лежит на прямой x+3у −5=0 . Тогда сторона CD лежит на прямой x+3y-m=0 (m - некоторое число), так как стороны параллельны. Две другие стороны AD и BC будут лежать на прямых вида 3х-у+n1=0 и 3х-у+n2=0, которые перпендикулярны прямым x+3у −5=0 и x+3y-m=0 . Так как ABCD - квадрат, расстояние от точки пересечения диагоналей (1,0) A − до всех его сторон, одинаково. Найдем его: Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти, используя следующую формулу: 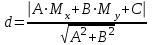 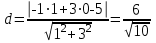 Теперь найдем неизвестные m, n1, n2, учитывая равенство расстояний от A до прямых: 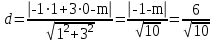 , откуда , откуда 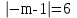 , значит m=5 (прямая АВ), или m=-7, то есть уравнение прямой CD имеет вид x+3у +7=0. , значит m=5 (прямая АВ), или m=-7, то есть уравнение прямой CD имеет вид x+3у +7=0.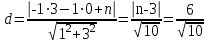 , откуда , откуда 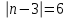 , значит, n1=9 и n2=-3, стороны АD и BC будут лежать на прямых 3х-у+9=0 и 3х-у-3=0 , значит, n1=9 и n2=-3, стороны АD и BC будут лежать на прямых 3х-у+9=0 и 3х-у-3=0 А В С D Ответ: АD : 3х-у+9=0 , BC : 3х-у-3=0, CD : x+3у +7=0 2.2.11. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая: 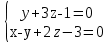 a) 5x+3y–z+2=0; б) 5x-3y–z+1=0; в) 5x+3y+2z-3=0; г) –x+5y+3z=0; д) 3х+5у–z–4=0. Сделать схематический чертеж. Решение: Найдем направляющий вектор исходной прямой 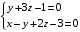 , для этого запишем исходное уравнение в параметрическом виде: , для этого запишем исходное уравнение в параметрическом виде: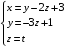 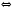 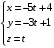 Тогда направляющий вектор исходной прямой 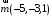 . .Для того, чтобы прямая была перпендикулярна плоскости необходимо, чтобы направляющий вектор прямой был коллинеарен нормальному вектору плоскости. Для плоскости а) 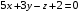 нормальный вектор нормальный вектор 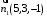 , который коллинеарен направляющему вектору исходной прямой , который коллинеарен направляющему вектору исходной прямой 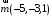 , т.к. , т.к. 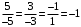 . .Для плоскости б) 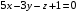 нормальный вектор нормальный вектор 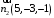 , который не коллинеарен направляющему вектору исходной прямой , который не коллинеарен направляющему вектору исходной прямой 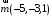 , т.к. , т.к. 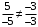 . .Для плоскости в) 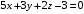 нормальный вектор нормальный вектор 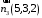 , который не коллинеарен направляющему вектору исходной прямой , который не коллинеарен направляющему вектору исходной прямой 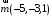 , т.к. , т.к. 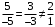 . .Для плоскости г) 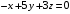 нормальный вектор нормальный вектор 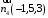 , который не коллинеарен направляющему вектору исходной прямой , который не коллинеарен направляющему вектору исходной прямой 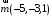 , т.к. , т.к. 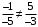 . .Для плоскости д) 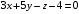 нормальный вектор нормальный вектор 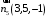 , который не коллинеарен направляющему вектору исходной прямой , который не коллинеарен направляющему вектору исходной прямой 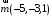 , т.к. , т.к. 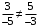 . .Следовательно, исходная прямая перпендикулярно плоскости а) 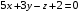 Для построения прямой возьмем две произвольные точки на ней, например при t=0, получаем точку 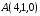 , при t=1 точку , при t=1 точку 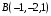 . .Для построения плоскости возьмем три произвольные точки на ней, например 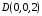 , , 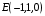 , , 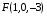 . .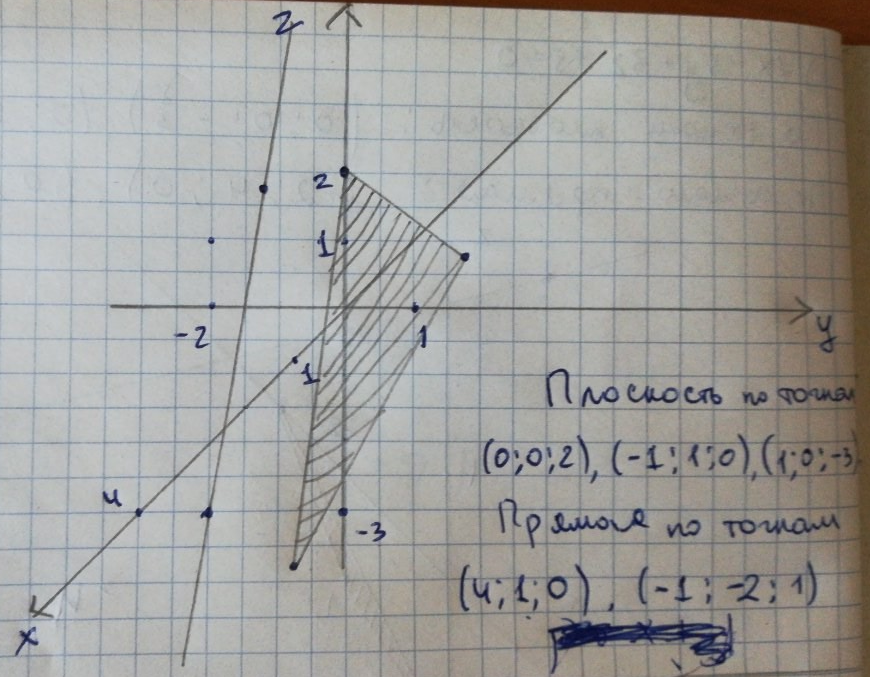 Ответ: плоскость а) 5x+3y–z+2=0 перпендикулярна прямой 3.3.31. Приведите к каноническому виду уравнения линий второго порядка. Установите тип этих линий и их расположение. Сделайте схематический чертеж. 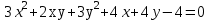 Решение: Для решения используем общее уравнение кривых вида: 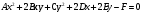 И выведем из него коэффициенты А,B,C,D,E,F: А=3, В=1, С=3, D=2, Е=2, F=-4 Найдём определитель 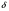 : :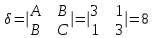 >0 эллиптический тип >0 эллиптический тип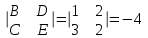 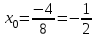 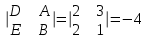 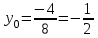 Сделаем замену (для вывода полного квадрата): 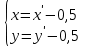 Значит, центр пересечения осей перенесется в точку (-0,5;-0,5) 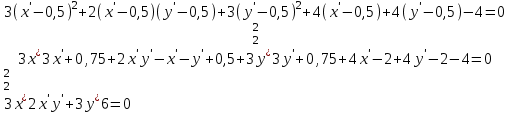 А=3, В=1, С=3 Найдём угол поворота  функции относительно оси координат с помощью следующей формулы: функции относительно оси координат с помощью следующей формулы: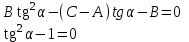 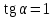 или или 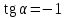 Будем рассматривать  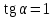 , тогда , тогда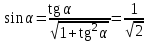 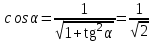 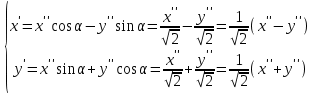 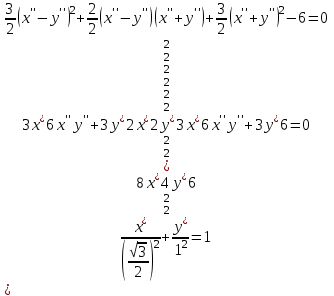 Получили уравнение эллипса, центр которого в т.(-0.5;-0.5) и повернутого на угол 45о 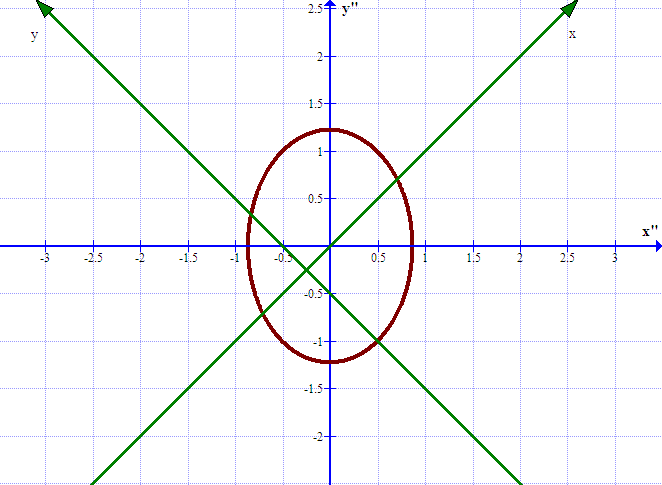 Ответ: эллипс, центр которого в т.(-0.5;-0.5) и повернутого на угол 45о 3.1.41 Решить систему линейных уравнений матричным методом и методом Гаусса. Сделать проверку. 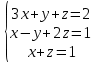 Решение: 1) Для решения матричным методом нужно рассмотреть матричное уравнение: AX = B, где A = 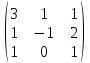 , X = , X = 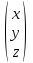 , B = , B = 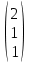 . Тогда X = A-1B. Найдем матрицу A-1. . Тогда X = A-1B. Найдем матрицу A-1. Вычислим обратную матрицу 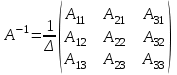 . .По формуле 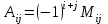 , где , где 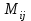 – минор (определитель полученный из исходной матрицы вычеркиванием i-той строки и j-того столбца) – минор (определитель полученный из исходной матрицы вычеркиванием i-той строки и j-того столбца)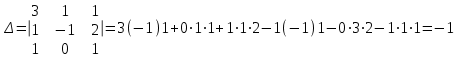
Тогда A-1 = 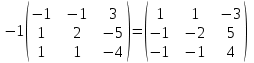 Сделаем проверку обратной матрицы: 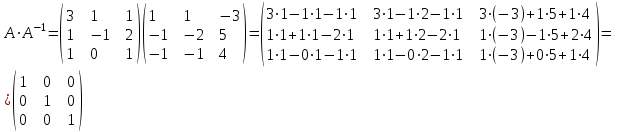 Получим X = A-1B = 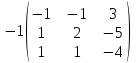 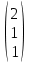 = = 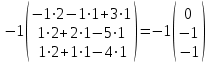 = =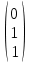 . .Получаем х=0, у=1, z=1. 2) Для решения системы методом Гаусса рассмотрим расширенную матрицу системы и приведем ее к треугольному виду: 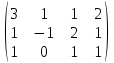 = поменяем местами первую и третью строчки = = поменяем местами первую и третью строчки =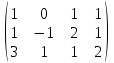 = [умножаем первую строчку на -1 и складываем со второй, умножаем первую на -3 и складываем с третьей] = = [умножаем первую строчку на -1 и складываем со второй, умножаем первую на -3 и складываем с третьей] = 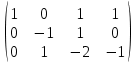 = складываем вторую строку с третьей] = = складываем вторую строку с третьей] = 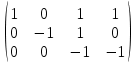 Получаем систему: 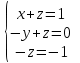 Получаем х=0, у=1, z=1. Проверка: Подставим полученные значения переменных в исходную систему уравнений: 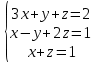 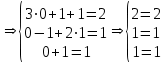 Получаем верные равенства Получаем верные равенстваОтвет: х=0, у=1, z=1 Контрольная работа №2 Введение в математический анализ. Производная и ее приложения. 6.2.31. Найти пределы функций, не пользуясь правилом Лопиталя. Решение: а) умножим и разделим на сопряженное значение для знаменателя 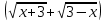 . .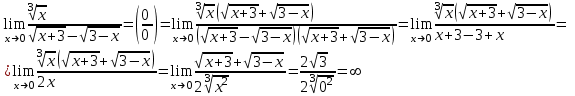 б) 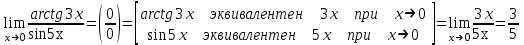 в) 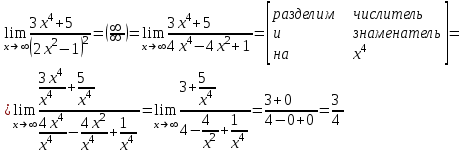 г) 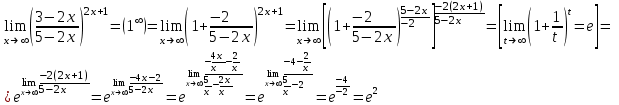 использовали второй замечательный предел 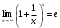 Ответ: а) , б) 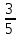 , в) , в) 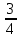 , г) , г) 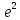 6.3.11. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать схематический чертеж. 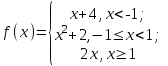 Решение. Данная функция определена для всех значений х 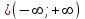 и на каждом из участков задания (-∞,-1), (-1,1), (1, +∞) является элементарной и, следовательно, непрерывной. Непрерывность функции может нарушиться лишь в точках, где изменяется ее аналитическое значение, то есть в точках х=-1 и х=1. Исследуем эти точки на непрерывность, находя односторонние пределы: и на каждом из участков задания (-∞,-1), (-1,1), (1, +∞) является элементарной и, следовательно, непрерывной. Непрерывность функции может нарушиться лишь в точках, где изменяется ее аналитическое значение, то есть в точках х=-1 и х=1. Исследуем эти точки на непрерывность, находя односторонние пределы: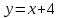  -1 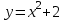 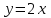 1 При х=-1 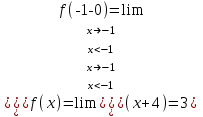 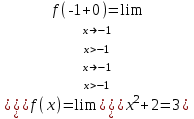 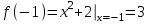  в точке х=-1 f(-1-0)=f(-1+0)=f(-1), значит х=0 точка непрерывности функции. При х=1 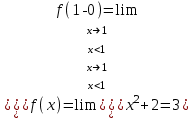 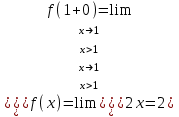 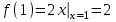 Так как в точке х=1 односторонние пределы – конечные числа, но не равны между собой, то х=1 – точка разрыва 1-го рода. Построим схематический график. 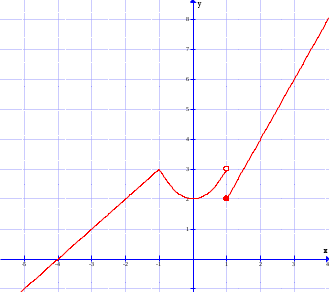 у=2х у=х2+2 у=х+4 Ответ: х=1 - точка разрыва первого рода. 7.1.1. Найдите производные 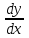 данных функций. данных функций.Решение: а) 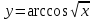 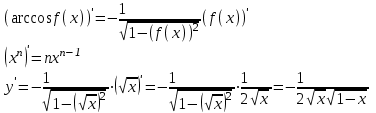 б) 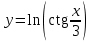 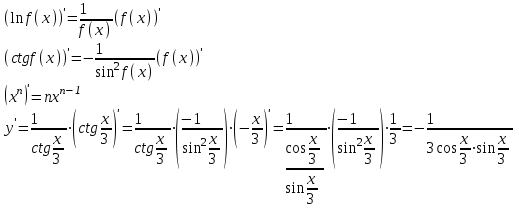 в) 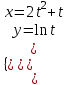 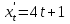 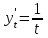 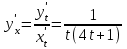 Ответ: a) 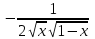 б) б) 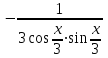 в) в) 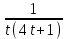 7.2.51. Требуется изготовить из жести ведро цилиндрической формы без крышки данного объёма. Каковы должны быть высота и радиус его дна, чтобы на его изготовление ушло наименьшее количество жести? Решение. П 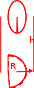 усть R –радиус основания цилиндра, h- высота. усть R –радиус основания цилиндра, h- высота.Площадь основания 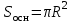 Площадь боковой поверхности 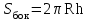 Т.к. объем цилиндра 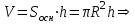 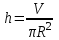 Составим функцию нахождения количества жести для бака 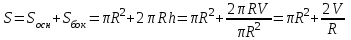 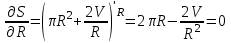 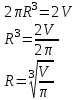 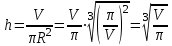 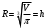 точка минимума функции, т.к. при точка минимума функции, т.к. при 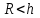 производная отрицательна, а при производная отрицательна, а при 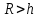 производная положительна. производная положительна.Ответ: 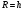 7.3.21. Методами дифференциального исчисления: а) исследовать функцию 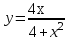 для для 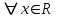 и по результатам исследования построить ее график; и по результатам исследования построить ее график;б) найти наименьшее и наибольшее значения заданной функции на отрезке [-3;3]. Решение. Область определения функции 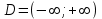 Точки пересечения с осями координат: Ох: 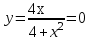 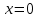 , получаем одну точку пересечения О(0;0) , получаем одну точку пересечения О(0;0) Оу: х=0 y=0 т.(0;0) – точка пересечения. Функция является нечетной, т.к. 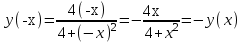 Экстремумы и монотонность. Вычисляем первую производную 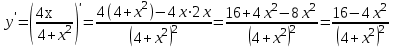 Находим критические точки 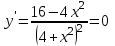 при х= при х=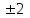
Функция убывает на промежутках (-∞;-2) и (2;+∞) , возрастает на промежутке (-2;2). В т.х=-2 минимум функции, в т.х=2 максимум. Выпуклость и точки перегиба. Вычислим вторую производную 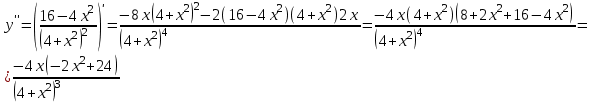 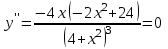 при х=0 х= при х=0 х=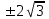
наклонные асимптоты вида у=kx+b 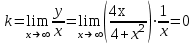 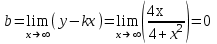 Прямая у=0 – горизонтальная асимптота 7. Строим график функции: 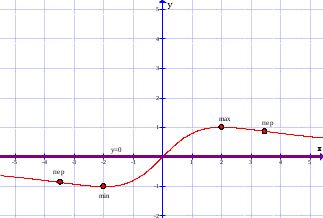 Б) На отрезке [-3;3] функция непрерывна и имеет на данном отрезке две точки экстремума х= 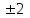 , значит наибольшее и наименьшее значение функции может быть достигнуто в точках экстремума и на концах отрезка. , значит наибольшее и наименьшее значение функции может быть достигнуто в точках экстремума и на концах отрезка.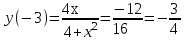 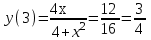 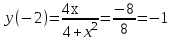 минимум функции на отрезке минимум функции на отрезке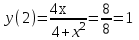 максимум функции на отрезке максимум функции на отрезкеКонтрольная работа №3 Неопределенный и определенный интегралы. Функции нескольких переменных. Кратные интегралы. 8.1.1. Найти неопределенные интегралы. Результаты проверить дифференцированием. Решение: а) Используем табличные интегралы и сразу получаем ответ: 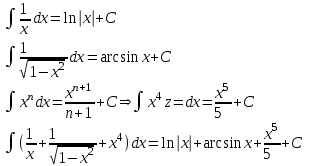 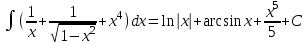 Проверка: 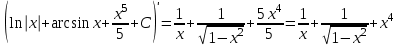  б) 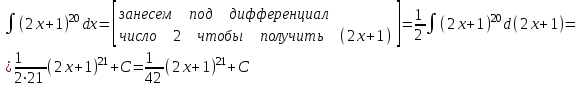 Проверка: 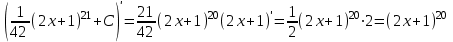 в) Используем формулу интегрирования по частям: 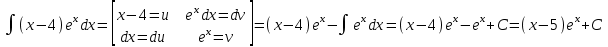 Проверка: 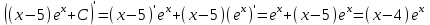 г) 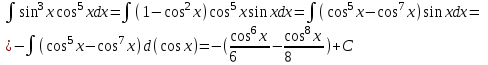 Проверка: 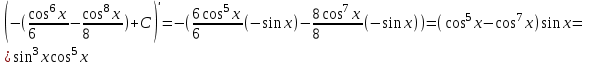 Ответ: а) 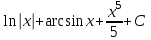 б) 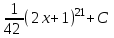 в) 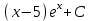 г) 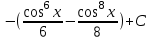 8.2.31 Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж. Решение: 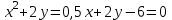 Сделаем чертеж. 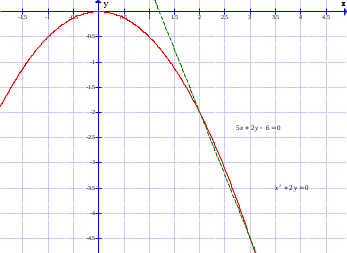 Вот эта маленькая область Пусть функции 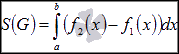 . .Найдем точки пересечения из решения системы уравнений: 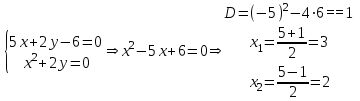 Тогда корни уравнения 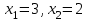 – это абсциссы точек пересечения графиков. – это абсциссы точек пересечения графиков.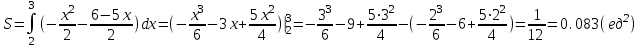 Ответ: Ответ: 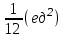 9.1.11 Найти производные функции двух переменных 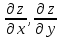 , если , если 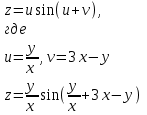 Решение: 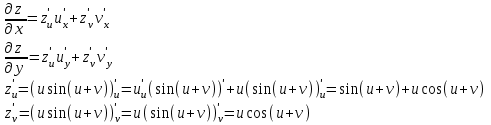 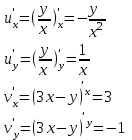 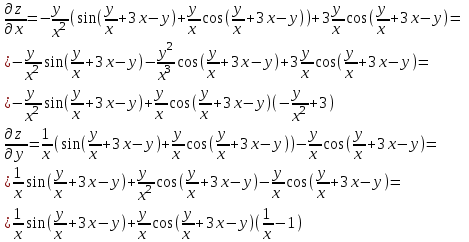 Ответ: 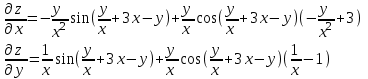 9.1.51 Расставить пределы интегрирования в повторном интеграле для двойного интеграла 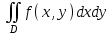 , и изменить порядок интегрирования. , и изменить порядок интегрирования. 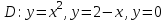 . .Решение: 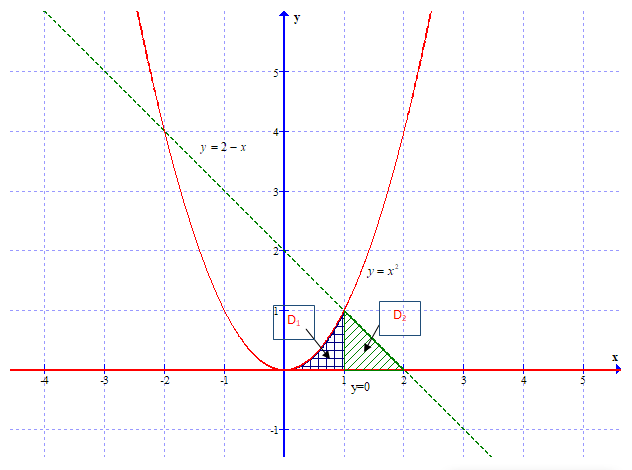 Найдем точки пересечения из решения системы уравнений: 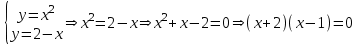 Значит, корни уравнения 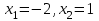 . Получим точки пересечения (-2,4) и (1,1) . Получим точки пересечения (-2,4) и (1,1)Если двигаться вдоль оси Оу, то у изменяется от 0 до 1, затем если двигаться по направлению оси Ох, то начала пересекается линия 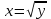 , а затем линия , а затем линия 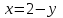 . .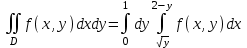 Изменим порядок интегрирования. Получим две области. Первая область: Если двигаться вдоль оси Ох, то х изменяется от 0 до 1. Затем если двигаться по направлению оси Оу, то начала пересекается линия 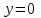 , а затем линия , а затем линия 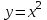 . . Вторая область: Если двигаться вдоль оси Ох, то х изменяется от 1 до 2. Затем если двигаться по направлению оси Оу, то начала пересекается линия 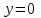 , а затем линия , а затем линия 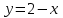 . .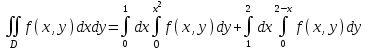 Итак, 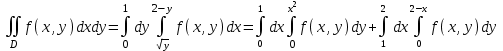 10.1.1 Вычислить криволинейный интеграл. Сделать чертеж кривой дуги L. 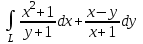 , где L– отрезок прямой от точки (1,0) до точки (2,1). , где L– отрезок прямой от точки (1,0) до точки (2,1). Решение: Найдем уравнение линии: 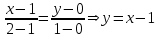 Сделаем чертеж. 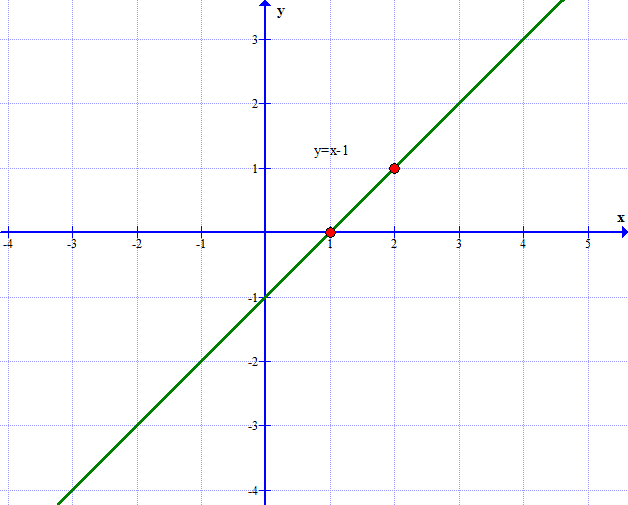 Значит, х изменяется от 1 до 2 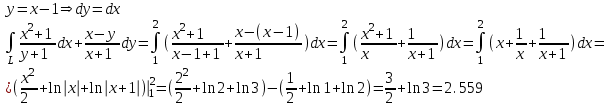 Ответ: 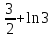 Список использованной литературы Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. – Т.1. –М.: Дрофа, 2007. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения, кратные интегралы. Ряды. Функции комплексного переменного. – Т.3. – М.: Дрофа, 2005. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. – Т. 1,2. – М.: Высшая школа,2002 . Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 2001. Лисичкин В.Т., Соловейчик И.Л. Математика. - Москва.: Высшая школа, 1991. Германова Е.Н. Высшая математика (дополнительный учебный материал). - Москва.: Связь, 1970. Зайцев И.Л. Элементы высшей математики. - Москва.: Наука, 1972. Богомолов Н.В., Сергиенко Л.Ю. Сборник дидактических заданий по математике. - Москва.: Высшая школа, 1987. |

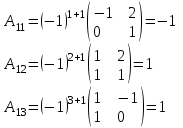
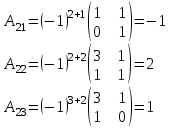
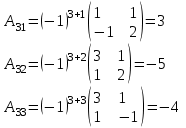
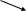
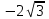 )
) )
)