лабараторная работа. лабораторная работа № 2. Косвенные измерения. Методические указания по проведению лабораторной работы по дисциплине Практическая метрология

Название	Методические указания по проведению лабораторной работы по дисциплине Практическая метрология
Анкор	лабараторная работа
Дата	08.03.2023
Размер	339.5 Kb.
Формат файла
Имя файла	лабораторная работа № 2. Косвенные измерения.doc
Тип	Методические указания #974428

Федеральное агентство по образованию РФ

Государственное образовательное учреждение высшего профессионального образования

«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
УТВЕРЖДАЮ
Декан электрофизического факультета

___________________ Г.С. Евтушенко

___________ ___________ 2010 г.

КОСВЕННЫЕ ОДНОКРАТНЫЕ ИЗМЕРЕНИЯ.

ОЦЕНИВАНИЕ ПОГРЕШНОСТЕЙ И НЕОПРЕДЕЛЕННОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЙ

Методические указания

к проведению лабораторной работы по дисциплине

«Практическая метрология»

для студентов всех специальностей

Томск 2010

Косвенные однократные измерения. Оценивание погрешностей и неопределенности результата измерений.

Методические указания по проведению лабораторной работы по дисциплине «Практическая метрология» для студентов всех направлений.

Составитель
Рецензент

Методические указания рассмотрены и рекомендованы к изданию методическим семинаром кафедры компьютерных измерительных систем и метрологии

«____» _________ 2010 г

Зав. кафедрой, проф., д.т.н. С.В. Муравьев

Введение
Подавляющее большинство технических измерений являются однократными. Выполнение однократных измерений обосновывают следующими факторами:

- производственной необходимостью (разрушение образца, невозможность повторения измерения, экономическая целесообразность и т.д.);

- возможностью пренебрежения случайными погрешностями;

- случайные погрешности существенны, но доверительная граница погрешности результата измерения не превышает допускаемой погрешности измерений;

- стандартная неопределенность, оцениваемая по типу А, существенна, но расширенная неопределенность не превышает заданного предела (см. раздел 2).

За результат однократного измерения принимают одно-единственное значение отсчета показания прибора. Будучи по сути дела случайным, однократный отсчет х включает в себя инструментальную, методическую и субъективную составляющие погрешности измерения, в каждой из которой могут быть выделены систематические и случайные составляющие погрешности.

В зависимости от характера проявления различают систематическую (

) и случайную (

) составляющие погрешности измерений, а также грубые погрешности (промахи).

Систематическая погрешность измерения ( ) – это составляющая погрешности результата измерений, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.

Случайная погрешность измерения ( ) - составляющая погрешности результата измерений, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.

Грубые погрешности (промахи) возникают из-за ошибочных действий оператора, неисправности СИ или резких изменений условий измерений (например, внезапное падение напряжения в сети электропитания).

В зависимости от вида источника возникновения погрешности рассматриваются следующие составляющие общей погрешности измерений:

Погрешности метода – это погрешности, обусловленные несовершенством метода измерений, приемами использования средств измерения, некорректностью расчетных формул и округления результатов, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений.

Инструментальные погрешности – это погрешности, зависящие от погрешностей применяемых средств измерений.

Исследование инструментальных погрешностей является предметом специальной дисциплины – теории точности измерительных устройств.

Субъективные погрешности – это погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при оценке центра интервала между двумя делениями и т.д.

При измерении с точным оцениванием погрешности проблема заключается в выявлении и оценке систематических и случайных составляющих погрешности полученного отсчета х с последующим их раздельным суммированием.

При измерении с приближенным оцениванием погрешности оценивание погрешностей производится на основе данных нормативных документов о свойствах используемых средств измерений (пределов допускаемой основной и дополнительной погрешностей). Такие оценки хотя и грубо, но все же дают возможность оценить погрешность.

Для приближенного оценивания погрешности измерения необходимы сведения о погрешностях (основной и дополнительной) средств измерений. Методические погрешности должны быть учтены заранее. Субъективные погрешности при однократных измерениях предполагаются малыми и их не учитывают.
1 Оценивание погрешности при косвенных измерениях.

При косвенных измерениях искомое значение величины находят расчетом на основе прямых измерений других физических величин, функционально связанных с искомой величиной известной зависимостью

(1.1)

где

– подлежащие прямым измерениям аргументы функции

.

Результатом косвенного измерения является оценка величины у, которую находят подстановкой в формулу (1.1) измеренных значений аргументов х_i.

Поскольку каждый из аргументов х_iизмеряется с некоторой погрешностью, то задача оценивания погрешности результата сводится к суммированию погрешностей измерения аргументов. Однако особенность косвенных измерений состоит в том, что вклад отдельных погрешностей измерения аргументов в погрешность результата зависит от вида функции (1.1).

Для оценки погрешностей существенным является разделение косвенных измерений на линейные и нелинейные косвенные измерения.

При линейных косвенных измерениях уравнение измерений имеет вид:

, (1.2)

где

– постоянные коэффициенты при аргументах х_i .

Результат линейного косвенного измерения вычисляют по формуле (1.2), подставляя в неё измеренные значения аргументов.

Погрешности измерения аргументов х_i могут быть заданы своими границами

.

При малом числе аргументов (меньше пяти) простая оценка погрешности результата

получается простым суммированием предельных погрешностей (без учета знака), т.е. подстановкой границ

х₁,

х₂,…,

х_n в выражение:

. (1.3)

Однако эта оценка является излишне завышенной, поскольку такое суммирование фактически означает, что погрешности измерения всех аргументов одновременно имеют максимальное значение и совпадают по знаку. Вероятность такого совпадения практически равна нулю. Для нахождения более реалистичной оценки переходят к статическому суммированию погрешности аргументов по формуле: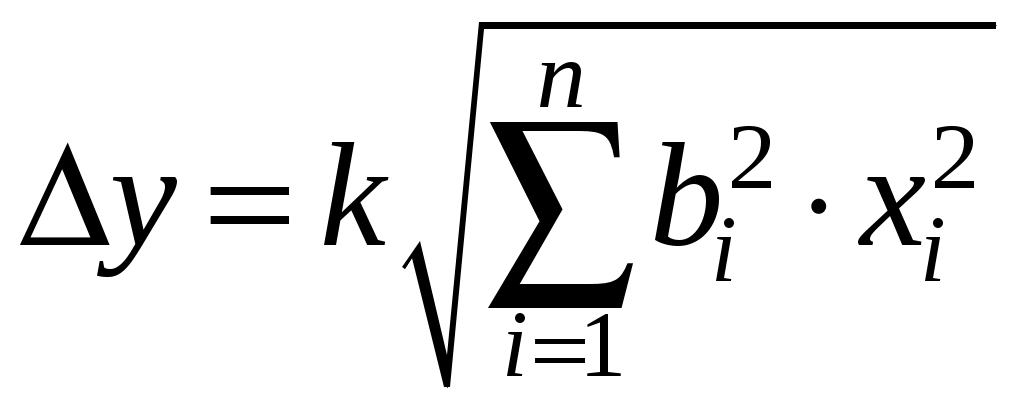

, (1.4)

где

– коэффициент, определяемый принятой доверительной вероятностью (при Р= 0,9 при k= 1,0; Р = 0,95 при k= 1,1; Р= 0,99 при k= 1,4).

Нелинейные косвенные измерения – любые другие функциональные зависимости, отличные от (1.2).

При сложной функции (1.1) и, в особенности, если это функция нескольких аргументов, определение закона распределения погрешности результата связано со значительными математическими трудностями. Поэтому в основе приближенного оценивания погрешности нелинейных косвенных измерений лежит линеаризация функции (1.1) и дальнейшая обработка результатов, как при линейных измерениях.

Запишем выражение для полного дифференциала функции у через частные производные по аргументам х_i:

. (1.5)

По определению полный дифференциал функции – это приращение функции, вызванное малыми приращениями её аргументов.

Учитывая, что погрешности измерения аргументов всегда являются малыми величинами по сравнению с номинальными значениями аргументов, можно заменить в формуле (1.5) дифференциалы аргументов

на погрешность измерений

, а дифференциал функции

на погрешность результата измерения

. (1.6)

Если проанализировать формулу (1.6), то можно получить простые правила оценивания погрешности результата нелинейного косвенного измерения:

- если результат измерений получается перемножением измерений

или делений измерений

, то для получения полной относительной погрешности складываются относительные погрешности каждого измерения

, где

;

- если результат измерений получается суммирование измерений

или вычитанием измерений

, то для получения полной погрешности складываются абсолютные погрешности каждого измерения

;

- если результат измерений возведен в степень, то для получения полной относительной погрешности показатель степени умножается на относительную погрешность измерения.
1.2 Погрешность записи числа

Погрешность записи числа определяется как отношение половины единицы младшего разряда числа к значению числа.

Например, для нормального ускорения падающих тел g = 9,81 м/с², единица младшего разряда равна 0,01, следовательно, погрешность записи числа 9,81 будет равна
δ

1.3 Правила округления погрешности и записи результатов измерений

В соответствии с МИ 1317 погрешность измерений выражается числом с одной или двумя значащими цифрами.

Эмпирически были установлены следующие правила округления рассчитанного значения погрешности и полученного результата измерения.

- если первая значащая цифра числа, выражающего погрешность, равна 1 или 2, то это значение погрешности должно содержать две значащих цифры. При этом округление проводится всегда в большую сторону.

- если первая значащая цифра числа, выражающего погрешность, равна 3 и более, то значение погрешности должно содержать одну значащую цифру. При этом округление проводится по законам математики.

- при записи результатов измерений числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности.

- округление производится лишь в окончательном ответе, все промежуточные вычисления производятся с одним, двумя лишними знаками.
2 Оценивание неопределенности измерений.

В соответствии с РМГ 43 неопределенность измерений - параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые могли бы быть обоснованно приписаны измеряемой величине.

Неопределенность результата измерения отражает отсутствие точного значения измеряемой величины, т.е. переменной. Результат измерения поправки на известные систематические эффекты все еще является только оценкой значения измеряемой величины, вследствие неопределенности, возникающей из-за случайных эффектов и неточной поправки результата на систематические эффекты. Результат измерения (после внесения поправки) может быть (неизвестно на сколько) очень близким к значению измеряемой величины, т.е. может иметь пренебрежимо малую погрешность, даже если он может иметь большую неопределенность. На практике существуют всевозможные источники неопределенности измерения, такие как:

- неполное определение измеряемой величины;

- несовершенная реализация определения измеряемой величины;

- непрезентативная выборка, т.е. измеренный образец может не представлять измеряемую величину;

- неадекватное знание эффектов от условий окружающей среды, влияющих на измерение, или несовершенное измерение условий окружающей среды;

- субъективная систематическая ошибка оператора при снятии показаний аналоговых средств измерений;

- разрешающая способность или порог чувствительности средств измерений;

- неточные знания констант и других параметров, взятых из внешних источников и используемых при обработке данных и другие.

Основным количественным выражением неопределенности измерений является стандартная неопределенность u. Стандартная неопределенность измерений - неопределенность результата измерений, выраженная в виде среднего квадратического отклонения.

Различают два типа вычисления стандартной неопределенности:

- вычисление по типу А - путем статистического анализа результатов многократных измерений;

- вычисление по типу В - с использованием других источников информации об измеряемом значение.
Исходными данными для вычисления неопределенности по типу А

являются результаты многократных измерений:

(где

;

- число измерений

-й входной величины).

Стандартную неопределенность единичного измерения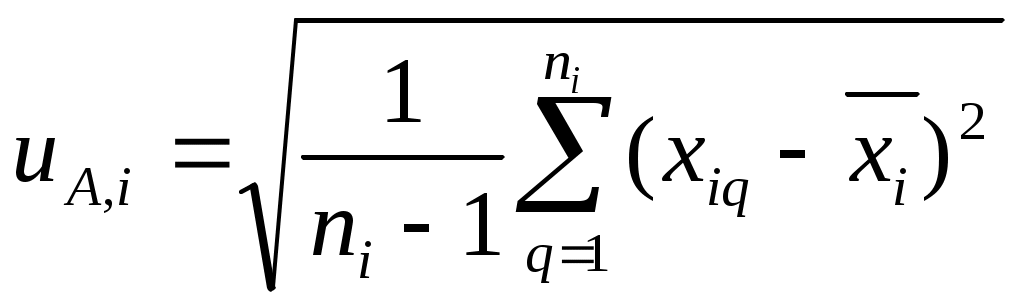

-й входной величины

вычисляют по формуле (1.7):

_{, (1.7)}

где

- среднее арифметическое результатов измерений

-й входной величины.

Стандартную неопределенность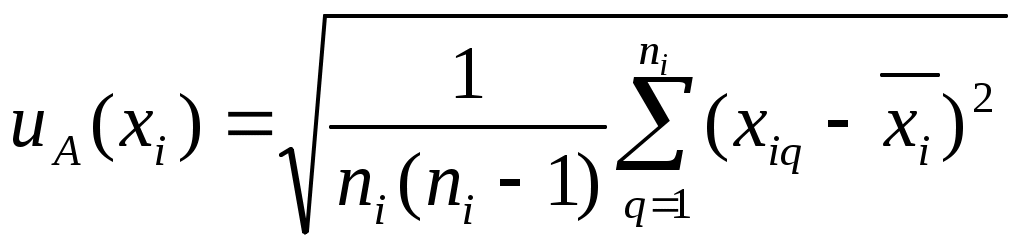

измерений

-й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле (1.8):

(1.8)
В качестве исходных данных для вычисления неопределенности по типу В

используют:

- данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;

- данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов;

- неопределенности констант и справочных данных;

- данные поверки, калибровки, сведения изготовителя о приборе и т.п.

Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных (нижней и верхней) границах [θ_i_-,θ_i₊] для

-й входной величины. При этом стандартную неопределенность, вычисляемую по типу В -

, определяют по формуле:

_{, (1.9)}

где θ_i - неисключенная систематическая погрешность, заданная границами ± θ.

а для симметричных границ (± θ_i) - по формуле:

_{, (1.10)}
Примечание - В случае других законов распределения формулы для вычисления неопределенности по типу В будут иными.
Для вычисления коэффициента корреляции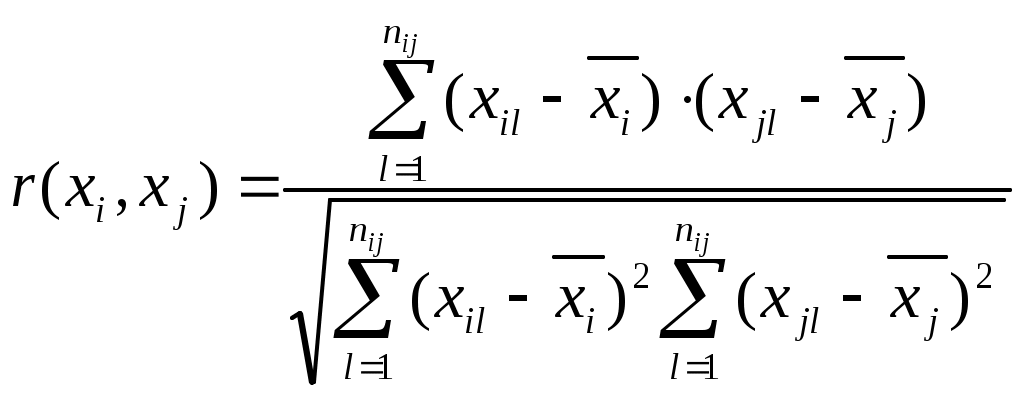

используют согласованные пары измерений

(где

;

- число согласованных пар результатов измерений):

_(1.11)

В большинстве случаев измеряемая величина у не является прямо измеряемой, а зависит от других измеряемых величин , входящих в функциональную зависимость вида

или в модель F(x,y) = 0. Тогда суммарную неопределенность можно рассчитать используя следующие формулы:

- в случае отсутствии корреляции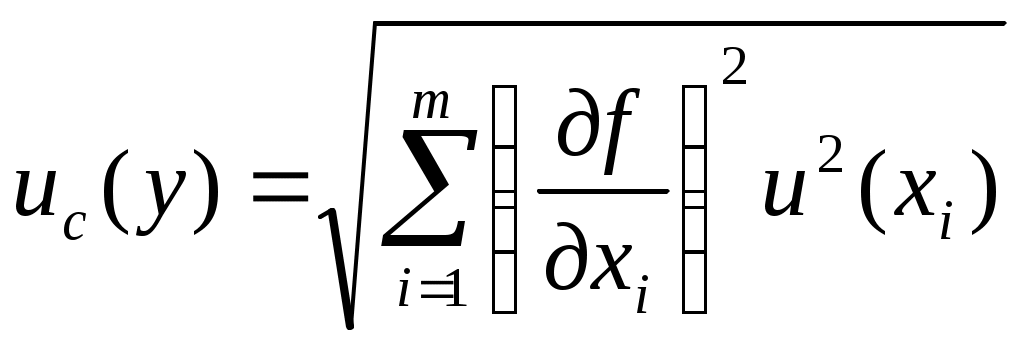

оценок суммарная стандартная неопределенность

определяется по формуле:

_{, (1.12)}

где с_i =

- коэффициенты чувствительности;

- стандартная неопределенность

-й входной величины, вычисленная по типу А или В.

- в случае коррелированных оценок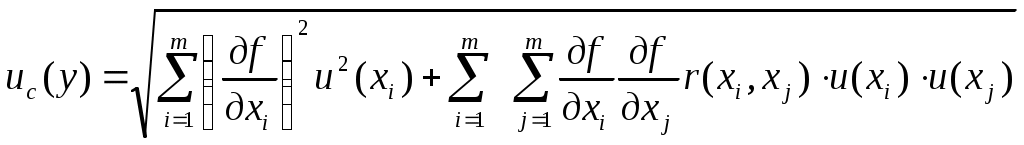

суммарную стандартную неопределенность вычисляют по формуле:

_(1.13)
где

- коэффициент корреляции;

- в случае положительно коррелированных оценок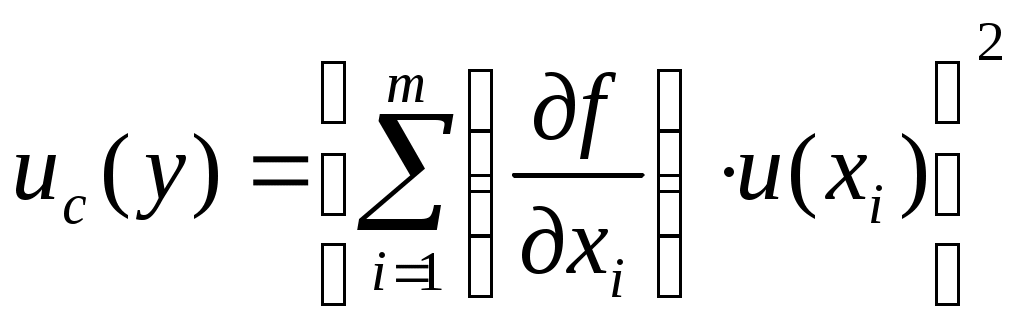

суммарную стандартную неопределенность вычисляют по формуле:

_(1.14)

- в случае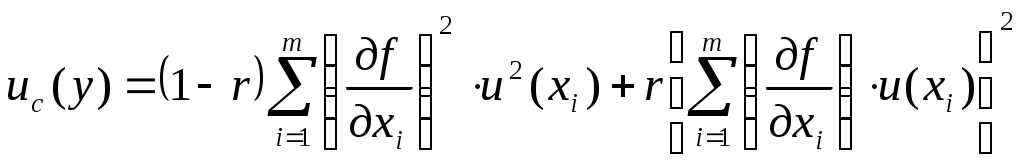

суммарную стандартную неопределенность вычисляют по формуле:

_(1.15)

Суммарная стандартная неопределенность может повсеместно использоваться для выражения неопределенности результата измерения, но в некоторых случаях в промышленности, торговле и регулирующих актах необходимо дать неопределенность в виде интервала для результата измерения, в пределах которого, можно ожидать, находится большая часть распределения значений, которые можно с достаточным основанием приписывать измеряемой величине. Из этого следует, что результатом измерения должен быть интервал, центром которого является искомое значение с данной вероятностью того, что в процессе повторных измерений оно будет находиться в пределах этого интервала. Такой интервал представляется с помощью расширенной неопределенности U. Значение расширенной неопределенности находиться по формуле:

_{, (1.16)}

где

- коэффициент охвата;

Если значения некоторой величины и ее стандартная неопределенность подчиняется нормальному закону распределения, то при числе степеней свободы

= ∞ коэффициент охвата k равен 2 при вероятности Р = 0,95.

Если вычисление значений входных величин и соответствующих стандартных неопределенностей осуществляется по методу типа А, а количество измерений равно n, то данное вычисление значений ограничено числом степеней свободы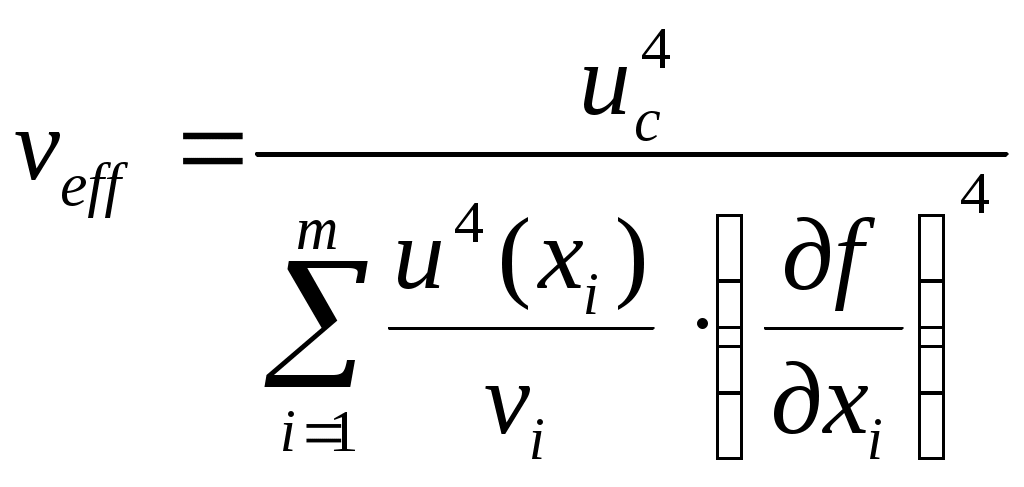

, то тогда коэффициент охвата рассчитывается по формуле:

_{, (1.17)}

где

- квантиль распределения Стьюдента с эффективным числом степеней свободы

и доверительной вероятностью Р;

- эффективная степень свободы, вычисляется по формуле:

_(1.18)
2.1 Правила округления неопределенности измерений

Округление неопределенности измерений проводится в соответствии с МИ 1317 (см. раздел 1.3).
Цель работы:

освоить методы проведения однократных прямых и косвенных измерений;
усвоить правила обработки, представления (записи) и интерпретации результатов проведенных измерений;
приобрести практические навыки применения различных по точности средств измерений, а также анализа и сопоставления точности результатов косвенных измерений с точностью средств измерений, используемых при проведении прямых измерений;
приобрести навыки оценивания погрешностей и неопределенности результата измерения;
приобрести навыки выявления возможных источников и причин методических погрешностей

Для подготовки к лабораторной работе изучить:

Р 50.2.038-2004 ГСИ. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений;
МИ 2083-90 ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей;
Руководство по выражению неопределенности измерений;
РМГ 43-2001 ГСИ. Применение «Руководства по выражению неопределенности измерений»;
МИ 1317-2004 ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях продукции и контроле их параметров

Используемое оборудование и материалы:

штангенциркуль;
микрометр;
линейка;
цилиндры разных объемов;
источник питания АТН 1232;
мультиметр АМ 1097;
мультиметр СХ-506;
универсальный вольтметр В7-22 А;
резистор;
лабораторный макет

Программа работы

1 Измерение геометрических величин

1.1 Измерить объем цилиндра, используя функциональную зависимость:

_{, (1)}

_{где π=3,14}_{- числовой коэффициент, представляющий собой иррациональное число;}

- диаметр цилиндра, мм;

- высота цилиндра, мм.

1.2 Произвести однократные измерения диаметра и высоты цилиндра средствами измерений различной точности: штангенциркулем, микрометром и линейкой. Результаты измерений записать в таблицу 1.
Таблица 1

_{цилиндр}

_{Средство измерений}

_{Результаты измерений}

_{Погрешность результата измерений}

_{Неопределенность}

_{измерений}

Диаметр

, мм

Высота

, мм

Объем

, мм

_Δ_с,_d_{, мм}

_Δ_с,_h_{, мм}

δ_V, %

, мм³

_U_в_,d_{, мм}

_U_в_,h_{, мм}

_U_с_{, мм}

_U_(Р)_{, мм}³

_{Малого размера}

_{штанген-}

_{циркуль}

_{Окончательный результат измерений при}_P_=0,95

мм³

_{микрометр}

_{Окончательный результат измерений при}_P_=0,95

мм³

_{Большого размера}

_{штанген-циркуль}

_{Окончательный результат измерений при}_P_=0,95

мм³

_{линейка}

_{Окончательный результат измерений при}_P_=0,95

мм³

1.3 Оценить погрешность результата измерений

_1.3.1 _{Оценить погрешность используемых СИ, используя нормативную или техническую документацию на средства измерений.}

_1.3.2 _{Оценить суммарную систематическую погрешность прямых однократных измерений (для высоты и диаметра цилиндра, измеренных разными СИ):}

_{, (}₂₎

где Δ_с_i - i-ая составляющая систематической погрешности измеряемой величины Х;

n - число составляющих систематической погрешности;

k - поправочный коэффициент, определяемый принятой доверительной вероятностью. При доверительной вероятности Р = 0,95 поправочный коэффициент принимают равный 1,1.

Полученные данные внести в таблицу 1.

1.3.2 Оценить относительную погрешность измерений, выраженную в относительных единицах

δ_V

(3)

Для определения относительной погрешности измерений δ_V необходимо формулу (3) преобразовать в удобную для расчета, используя формулу (1.6).

В полученной формуле

- погрешности средств измерений, используемых при измерениях, Δπ - погрешность округления числового коэффициента π.

При косвенных измерениях физических величин очень часто используются табличные данные или иррациональные константы. В силу этого используемое при расчетах значение константы, округленное до некоторого знака, является приближенным числом, вносящим свою долю в погрешность измерений. Эта доля погрешности определяется как погрешность записи (округления) константы (см. п. 1.2 «Введение»).

1.3.3 Оценить погрешность вычисления объема по формуле:

δ_v

, мм³ (4)
Данные записать в таблицу 1.

1.3.4 Округлить погрешности измерений и записать результат измерений объёмов цилиндров

, мм³ (5)

Окончательный результат и погрешность косвенных измерений, необходимо округлить в соответствии с МИ 1317 (см. п.1.3 «Введение»).

Данные занести в таблицу 1.

1.3.5 Изобразить на рисунках области, в которых находятся результаты измерений объемов, полученные разными средствами измерений для каждого из цилиндров.
1.4 Оценить неопределенность измерений

1.4.1Оценить стандартную неопределенность по типу В для измерений диаметра и высоты цилиндров по формуле (1.10). Данные занести в таблицу 1.

1.4.2Оценить суммарную неопределенность измерения по типу В по формуле (1.12):

_{Дать обоснование выбора формулы расчета суммарной неопределенности измерения.}

1.4.3Определить и обосновать выбор значения коэффициента охвата.

1.4.4Оценить расширенную неопределенность при доверительной вероятности Р = 0,95 по формуле (1.16).

1.4.5Записать результат измерений в соответствии с правилами округлениями неопределенности, данные занести в таблицу 1.

, мм³ (6)
Окончательный результат и неопределенность косвенных измерений, необходимо округлить в соответствии с МИ 1317 (см. п.1.3 «Введение»).
2 Измерение электрических величин

2.1 Измерить постоянный ток, используя функциональную зависимость:

_{, (}₇₎

где U напряжение на сопротивлении ;

R сопротивление.

2.2 Произвести однократные измерения напряжения на сопротивлении и номинального значения сопротивления средствами измерений различной точности в соответствии с рисунком 1: мультиметром АМ 1097, мультиметром СХ-506, универсальным вольтметром В7-22 А.

2.3 Для проведения эксперимента собрать схему, представленную на рисунке 1. На источнике питания АТН 1232 установить значения напряжения в диапазоне (0-30) В.

2.3.1 Измерить напряжение на сопротивлении мультиметром СХ-506. Отключить источник питания АТН 1232 от лабораторного макета. Перевести мультиметр СХ-506 в режим измерения сопротивления и измерить номинальное значение сопротивления.

Результаты измерений занести в таблицу 2.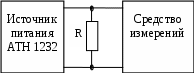

Рисунок 1
2.3.2 Измерить напряжение на сопротивлении мультиметром АМ 1097. Отключить источник питания АТН 1232 от лабораторного макета. Перевести мультиметр АМ 1097 в режим измерения сопротивления и измерить номинальное значение сопротивления.

Результаты измерений занести в таблицу 2.

2.3.3 Измерить напряжение на сопротивлении универсальным вольтметром В7-22 А. Отключить источник питания АТН 1232 от лабораторного макета. Перевести универсальным вольтметром В7-22 А в режим измерения сопротивления и измерить номинальное значение сопротивления.

Результаты измерений занести в таблицу 2.
Таблица 2

_{Средство измерений}

_{Результаты измерений}

_{Погрешность результата измерений}

_{Неопределенность}

_{измерений}

Напря-жение, U, B

Сопро-тивление,R, Ом

Ток,

I, А

_Δ_с,_U_,_B

_Δ_с,_R_,_O_м

δ_I, %

ΔI, A

_U_в_{, U}_,_B

_U_в_{, R}_,_O_м

_U_с_,_A

_U_(Р)_,_A

_{Мультиметр СХ-506}

_{Окончательный результат измерений при}_P_=0,95

_{Мультиметр АМ 1097}

_{Окончательный результат измерений при}_P_=0,95

_{Универсальный вольтметр В7-22А}

_{Окончательный результат измерений при}_P_=0,95

_2.4_{Оценить погрешность результата измерений}

_2.4.1_{Перечислить и определить составляющие систематической погрешности прямых однократных измерений напряжения и сопротивления для двух экспериментов. Полученные данные систематической погрешности занести в таблицу 2.}

2.4.2Оценить относительную погрешность измерений, выраженную в относительных единицах

δ_I

(8)

Для определения относительной погрешности измерений δ_I необходимо формулу (8) преобразовать в удобную для расчета, используя формулу (1.6).

В полученной формуле

– погрешности средств измерений, используемых при измерениях.

2.4.3Оценить погрешность вычисления сопротивления по формуле:

δ_I I₍₉₎

Окончательный результат и погрешность косвенных измерений, необходимо округлить в соответствии с МИ 1317. Данные занести в таблицу 2.

А

2.5.4 Изобразить на рисунках области, в которых находятся результаты измерений постоянного тока, полученные разными средствами измерений для каждого эксперимента.
2.5 Оценить неопределенность измерений

2.5.1Оценить стандартную неопределенность по типу В измерения падения напряжения на сопротивлении и сопротивления по формуле (1.10). Данные расчета занести в таблицу 2.

2.5.2Представить в удобной форме и оценить суммарную неопределенность измерения по типу В по формуле (1.12). Дать обоснование выбранной формуле.

2.5.3Определить и обосновать выбор значения коэффициента охвата.

2.5.4Оценить расширенную неопределенность при доверительной вероятности Р=0,95 по формуле (1.16).

2.5.5Записать результат измерений в соответствии с правилами округлениями неопределенности (см. п. 2.1 «Введение»), данные занести в таблицу 2.

A
3Составить отчет о проделанной работе.

Отчет о проделанной работе выполняется один на подгруппу. Отчет должен включать в себя:

титульный лист оформленный в соответствии с приложением В стандарта организации СТО ТПУ 2.3.05 – 2006 «Система образовательных стандартов. Занятия лабораторные. Общие требования к организации и проведению»;
цель работы;
используемое оборудование и материалы;
результаты измерений и вычислений, представленные в виде таблиц, расчетов и т.д.;
выводы.

В выводах дать обоснование различия полученных результатов измерений, выявить возможные источники и причины их возникновения. Сравнить погрешность и неопределенность измерений.