Итоговый. Методические указания по решению задач Омск 2004 Составители Ласица Александр Михайлович Кондратьева Тамара Николаевна

• Название: Методические указания по решению задач Омск 2004 Составители Ласица Александр Михайлович Кондратьева Тамара Николаевна
• Анкор: Итоговый.doc
• Дата: 01.12.2017
• Размер: 2.6 Mb.
• Имя файла: Итоговый.doc
• Тип: Методические указания; #10576
• Категория: Физика
• страница: 2 из 4

= 50 Гц. Радиус ротора a = 0,5 м. Определить давление газа на стенку ротора, если в его центре давление p₀ = 10⁵ Па. Температуру по всему объёму считать постоянной, равной Т=300 К.

Дано: = 50 Гц a = 0,5 м. p0= 105 Па. Т=300 К.

p -?

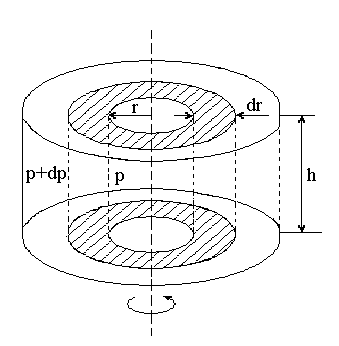Р ешение:

Рассмотрим находящийся в центрифуге цилиндрический слой воздуха бесконечно малой толщины dr, такой, что можно считать, что все молекулы данного слоя находятся на одинаковом расстоянии r от оси вращения.

Запишем для данного слоя второй закон Ньютона :

F = ma

Под силой F в данном случае нужно понимать разность сил давления действующих с внешней и внутренней стороны слоя

F = ((p+dp)-p)2r h = dp 2r h,

где произведение 2r h даёт площадь боковой поверхности слоя воздуха. Массу данного слоя можно получить, умножив плотность воздуха  на объём слоя dV = 2r dr h; m = dV =2r dr h. Все молекулы данного слоя вовлечены во вращательные движения с угловой скоростью и находятся на одинаковом расстоянии r от оси вращения, следовательно, обладают одинаковым нормальным ускорением . Объединяя выражения, получим

dp =dr·

(в правой и левой части сокращён одинаковый множитель 2r h). Из уравнения Менделеева–Клапейрона следует . Подставляя в предыдущее выражение и разделяя переменные, получим .

Проинтегрируем полученное уравнение:



где А - некоторая постоянная интегрирования. Представим её в виде натурального логарифма от некоторой другой постоянной С:A = ln C. Тогда



или .

По условию задачи на оси центрифуги давление должно быть p₀, это возможно только в случае, когда C= p₀. Заменяя C на p₀, определим давление как функцию расстояния до оси вращения:

.

Вспоминая, что , получим расчетную формулу для давления

.

Подставляя в последнюю формулу r = a = 0,5 м и молярную массу радона

= 0,222 кг/моль, вычислим давление газа на стенку центрифуги p = 3 10⁵ Па.

Ответ: давление на стенку ротора p₀ =3 10⁵ Па.

Задача № 4

Стальной стержень длиной ℓ = 20 см с площадью поперечного сечения S = 3 см² нагревается с одного конца до температуры t₁ = 300⁰С, а другим концом упирается в лёд. Предполагая, что передача тепла происходит исключительно вдоль стержня (без потерь через стенки), подсчитать массу льда, растаявшего за время t = 10 мин. Теплопроводность стали  = 60 Вт/(м∙К).

Дано: t1 = 3000С S = 3см2 t2 = 00С ℓ = 20см. = 10мин. = 60 Вт/м∙К

m -?

Решение:

Найдём количество теплоты полученное льдом. Для этого запишем уравнение теплопроводности.

.

Считая, что поток тепла не изменяется со временем и постоянен в пределах сечения стержня, данную формулу можно записать в виде

.

Производная представляет собой градиент температуры в стержне. Так как длина стержня равна ℓ, а разность температур на его концах t₁-t₂, можно произвести замену . Знак минус в выражении Q можно не учитывать, так как он показывает, что направление переноса теплоты противоположно направлению возрастания температуры. С учётом этого количество теплоты получённое льдом:

.

Так как всё это количество теплоты идёт на плавление льда, Q = m ( = 3,310⁵ Дж/кг – удельная теплота плавления льда). Объединяя выражения и производя расчеты получим

Ответ: масса растаявшего льда m = 0,049 кг = 49 г.

Задача № 5

В результате некоторого процесса вязкость некоторого идеального газа увеличилась в раза, а коэффициент диффузии – в раза. Во сколько раз увеличилось давление газа.

Дано: =

-?

Решение:

Согласно молекулярно кинетической теории,

, ,

где 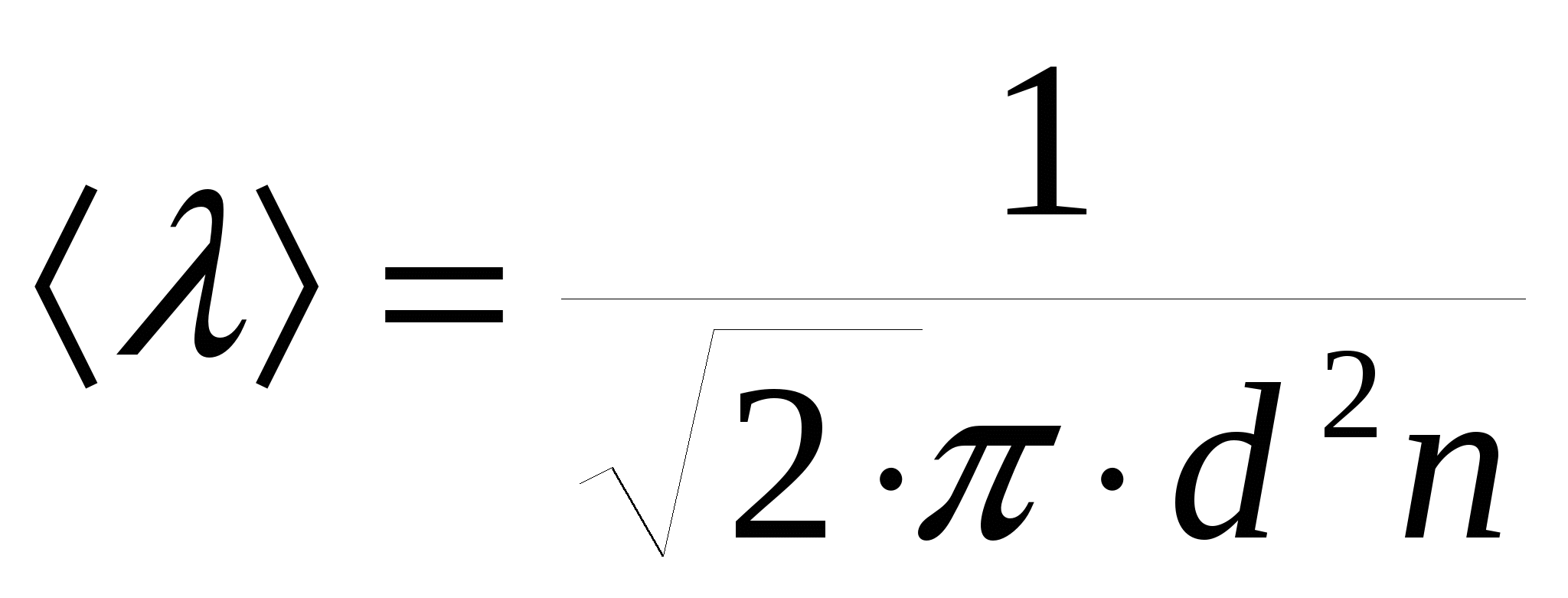 средняя длина свободного пробега, - средняя скорость движения молекул, =m₀n- плотность газа.

По основному уравнению МКТ , поэтому . Подставим в выражение для  значения , и , тогда

;

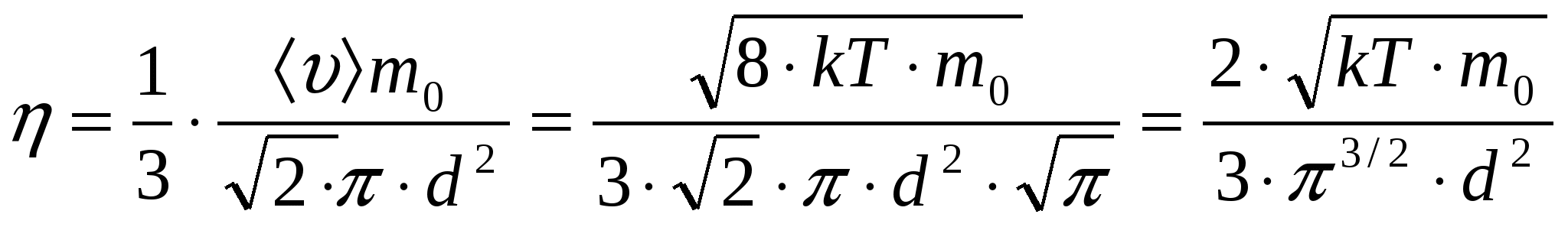Из формул видно, что , значит, . Для того чтобы найти отношение , свяжем между собой и D. Из формул видно, что . Отсюда , а отношение . В итоге получаем отношение давлений .

Ответ: давление возрастет в два раза.

Задачи, рекомендуемые для аудиторных занятий

1. 12 г газа занимают объем 4 дм³ при температуре 7⁰С. После нагревания газа при постоянном давлении его плотность стала равна 0,6 мг/см³. До какой температуры нагрели газ?

Ответ: до 1400 К.
2. В сосуде находится 14 г азота и 9 г водорода при температуре 10⁰С и давлении 1 МПа. Найти молярную массу смеси и объем сосуда.

Ответ: 4,6 г/моль; 12 дм³.
3. В двух сосудах емкостями 3 и 4 л находится газ под давлениями 0,2 и 0,1 МПа соответственно. Температура в обоих сосудах одинакова. Под каким давлением будет находиться газ, если соединить сосуды трубкой?

Ответ: 140 кПа.
4. В баллоне емкостью 150 см³ содержится газ при температуре 30 ⁰С. Вследствие утечки из колбы вышло 4∙10¹⁸ молекул. Определить, на сколько понизилось при этом давление газа?

Ответ: 112 Па.
5. Плотность некоторого газа равна 6∙10^-2 кг/м³, средняя квадратичная скорость молекул этого газа равна 500 м/с. Найти давление, которое газ оказывает на стенки сосуда.

Ответ: 5 кПа.
6. В баллоне емкостью 5 л находится 25∙10²¹ молекул азота. Найти среднюю квадратичную скорость его молекул, если давление в баллоне P = 720 мм рт.ст.

Ответ: 1100 м/с.
7. Найти число молекул азота в 1 см³ при нормальных условиях и обладающих скоростью: а) между 99 м/с и 101 м/с; б) между 499 м/с и 501 м/с.

Ответ: 8,6∙10¹⁸; 4,9∙10¹⁹.

8. Найти для газообразного азота температуру, при которой скоростям молекул υ₁ = 300 и υ₂ = 600 м/с соответствуют одинаковые значения функции распределения Максвелла.

Ответ: 330 К.
9. Полагая температуру воздуха и ускорение свободного падения не зависящими от высоты, определить, на какой высоте h над уровнем моря плотность воздуха меньше своего значения на уровне моря в 2 раза. Температура воздуха t= 0⁰С.

Ответ: 5,5 км.
10. Вычислить среднюю длину свободного пробега молекул воздуха при температуре 17 ⁰С и нормальном давлении. Эффективный диаметр молекул воздуха принять равным 3∙10^-8 см.

Ответ: 10^-7 м.
11. Определить среднее число всех столкновений между молекулами, которые происходят в течение 1 с в 1 см³ кислорода при температуре 17 ⁰С и давлении 5 мм рт. ст. Эффективный диаметр молекулы кислорода 2,9∙10^-8 см.

Ответ: 2,27∙10²⁴.
12. Найти среднюю длину свободного пробега азота, если его динамическая вязкость 17 мкПас, d = 0,3 нм.

Ответ: 0,09 нм.
13. Найти коэффициент теплопроводности воздуха при температуре 10 ⁰С и давлении 100 кПа, если диаметр молекулы воздуха принять равным 0,3 нм.

Ответ: 13 мВт/(мּК).
14. Вычислить коэффициент диффузии и динамическую вязкость азота при давлении 0,1 МПа и температуре 7 ⁰С.

Ответ:14ּ10^-6 м²/с и 17ּ10^-6 Паּс.

Задачи для самостоятельного решения

1. 
   Сколько молекул содержится в 2 л кислорода, находившегося при температуре 17⁰С и давлении 0,2 МПа?
   
2. 
   Сосуд емкостью 1 л содержит 1,5 г некоторого газа под давлением 0,25 МПа. Определить среднюю квадратичную скорость молекул газа.
   
3. 
   Среднеквадратичная скорость молекул газа при давлении 0,1 МПа составляет 500 м/с. Определить плотность газа при этих условиях.
   
4. 
   При какой температуре средняя квадратичная скорость атомов гелия станет равной второй космической скорости (11,2 км/с)?
   
5. 
   Определить массу одной молекулы углекислого газа.
   
6. 
   В сосуде емкостью 5 л находится 0,2 моля некоторого газа. Определить, какой это газ, если его плотность 1,12 кг/м³.
   
7. 
   Газ при температуре 309 К и давлении 0,7 МПа имеет плотность 12 кг/м³. Определить молярную массу этого газа.
   
8. 
   Сколько молекул газа содержится в баллоне вместимостью 30 л при температуре 300 К и давлении 5 МПа?
   
9. 
   Плотность некоторого газа 0,06 кг/м³, средняя квадратичная скорость молекул этого газа 500 м/с. Найти давление, которое газ оказывает на стенки сосуда.
   
10. 
    Давление газа 1 МПа; концентрация молекул 10¹⁰ см^-1. Найти температуру газа и среднюю кинетическую энергию поступательного движения одной молекулы.
    
11. 
    Плотность воздуха при температуре 0 ⁰С и давлении 760 мм рт. ст. равна 0,001293 г/см³. Сколько весит литр воздуха при температуре 27,3 ⁰С и давлении 750 мм рт. ст.?
    
12. 
    Баллон содержит газ при t₁ = 50⁰С и давлении 30 атм. Каково давление, когда из баллона будет выпущена половина массы газа, а температура понизится до t₂ = 10 ⁰С?
    
13. 
    Сосуд ёмкостью V = 0,01 м³ содержит азот массой m₁ = 7 г и водород массой m₂ = 1 г при температуре Т = 280 К. Определить давление P смеси газов.
    
14. 
    Найти плотность ρ газовой смеси, состоящей по массе из одной части водорода и восьми частей кислорода, при давлении P = 0,1 МПа и температуре Т = 290 К.
    
15. 
    Баллон емкостью V = 15 л содержит смесь водорода и азота при температуре Т = 300 К и давлении P = 1,23 МПа. Масса смеси m = 145 г. Определить массу m₁ водорода и массу m₂ азота.
    
16. 
    Газовая смесь, состоящая из кислорода и азота, находится в баллоне под давлением P = 1 МПа. Считая, что масса кислорода составляет 20% от массы смеси, определить парциальные давления P₁иP₂от дельных газов.
    
17. 
    Два сосуда с объемами V₁ = 1 л и V₂ = 3 л соединены трубкой с краном. До открытия крана в первом сосуде содержался азот под давлением P₁ = 0,5 атм и при температуре t₁ = 0 ⁰С, а во втором - аргон под давлением P₂ = 1,5 атм и при температуре t₂ = 100 ⁰С. Определить, какое давление установится в смеси газов, если открыть кран. Температура смеси 79 ⁰С.
    
18. 
    Плотность газа ρ при давлении P = 720 мм рт. ст. и температуре t₂ = 0 ⁰С равна 1,3 г/л. Найти массу моля μ газа.
    
19. 
    Сколько молекул водорода находится в объеме 1,55 л при температуре 27⁰С и давлении 750 мм рт. ст.?
    
20. 
    Найти число молекул Nв 1 см³ и плотность ρ азота при давлении 1,0010^-11 мм рт. ст. и температуре 15 ⁰С.
    
21. 
    Два баллона соединены трубкой с краном. В первом находится газ под давлением 10⁵ Н/м², во втором – при 6ּ10⁴ Н/м². Емкость первого баллона 1 л, второго – 3 л. Какое давление установится в баллонах (в мм рт. ст.), если открыть кран? Температуре постоянна. Объемом трубки можно пренебречь.
    
22. 
    Найти число ν молей и число N молекул, содержащихся в объеме V = 1см³ водяного пара при температуре t = 4 ⁰С.
    
23. 
    В баллоне емкостью V = 20 л находится аргон под давлениемP₁ = 800 кПа и температуре Т₁ = 325 К. когда из баллона было взято некоторое количество аргона, давление в баллоне снизилось до P₂ = 600 кПа, а температура установилась Т₂ = 300 К. Определить массу mаргона, взятого из баллона.
    
24. 
    Баллон емкостью V = 40 л заполнен азотом. Температура азота Т = 300 К. Когда часть азота израсходовали, давление в баллоне понизилось на ∆P = 400 кПа. Определить массу израсходованного азота. Процесс считать изотермическим.
    
25. 
    В баллоне находился идеальный газ при давлении 4ּ10⁷ Па и температуре 300 К. Затем 3/5 содержащегося в баллоне газа выпустили, а температура понизилась до 240 К. Под каким давлением находится оставшийся в баллоне газ?
    
26. 
    Какой объем