Итоговый. Методические указания по решению задач Омск 2004 Составители Ласица Александр Михайлович Кондратьева Тамара Николаевна
 Скачать 2.6 Mb. Скачать 2.6 Mb.
|
|
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА Методические указания по решению задач Омск 2004 Составители: Ласица Александр Михайлович; Кондратьева Тамара Николаевна; Павловская Ольга Юрьевна. Печатается по решению редакционно-издательского совета Омского государственного технического университета. Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяются два качественно различных метода: статистический и термодинамический. Первый лежит в основе молекулярной физики, второй – термодинамики. Основные положения молекулярной физики Молекулярная физика – раздел физики, изучающий строение и свойства вещества, исходя из молекулярно–кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном движении. Наиболее полное описание любой системы состояло бы в определении уравнений движения всех тел, входящих в нее, однако из-за большого числа частиц входящих в макроскопическую систему, данная задача является принципиально неразрешимой. Состояние системы в молекулярной физике определяется небольшим набором величин, называемых параметрами состояния (термодинамическими параметрами) характеризующих свойства системы в целом. В качестве основных параметров состояния выбирают температуру Т, давление р и объем V. Если система находится во внешнем поле, то к параметрам состояния добавляются характеристики поля. Параметры состояния в большинстве случаев не являются независимыми, они связаны между собой некоторым уравнением, называемым уравнением состояния. Одной из основных задач молекулярной физики является установление явного вида уравнения состояния и установление связи между параметрами состояния и усредненными характеристиками движения частиц, входящих в систему. Для решения такой задачи приходится прибегать к рассмотрению различных физических моделей вещества. Одной из самых простых моделей является модель идеального газа. Идеальным называют газ, удовлетворяющий следующим условиям:
Модель идеального газа можно использовать при изучении реальных газов, так как в условиях, близких к нормальным, а также при низких давлениях и высоких температурах они близки к идеальному газу. Кроме того, внеся поправки на собственный размер молекул и действующие молекулярные силы, можно перейти к теории реальных газов. Уравнение состояния идеального газа носит название уравнение Менделеева -Клапейрона и имеет вид 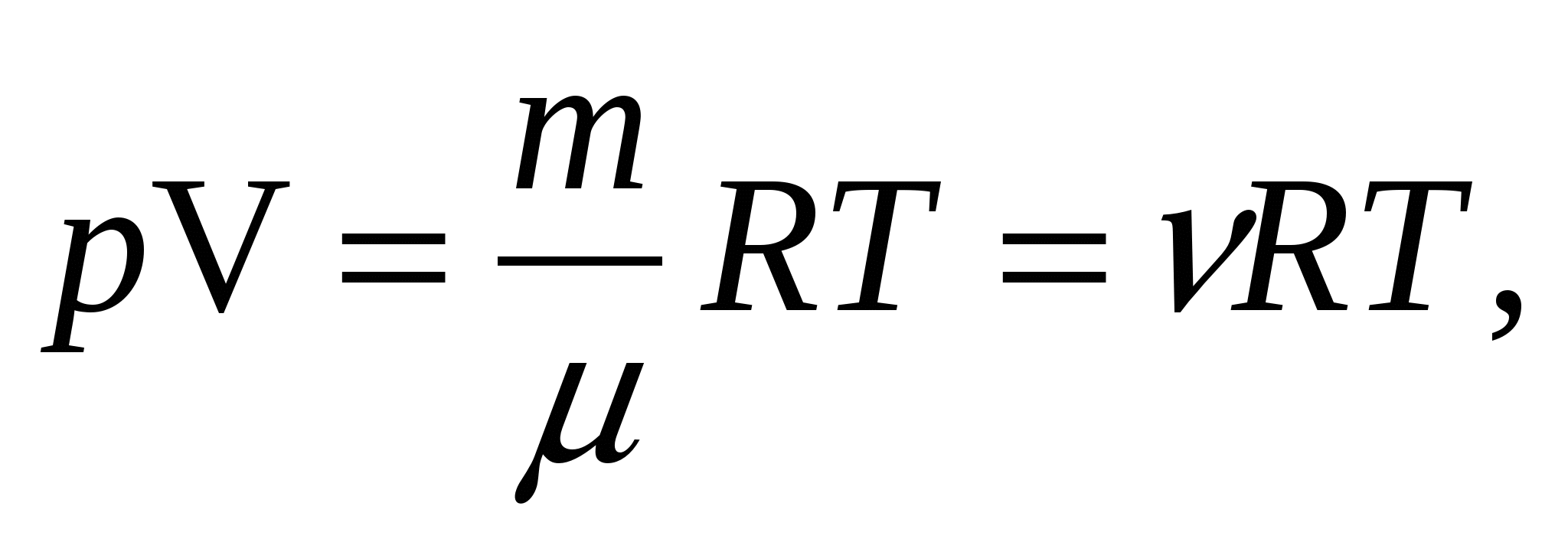 где =m/число молей газа, R=8,31 Дж/(мольК)универсальная газовая постоянная. Данное уравнение является обобщением установленных экспериментально законов поведения идеального газа к которым относятся законы:
p = p1 + p2 + p3 +, (р1, р2,…- парциальные давления – давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре);
По определению, в одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро: NA = 6,0221023 моль-1. Уравнение Менделеева - Клапейрона может быть переписано в другом виде: где n – концентрация молекул газа, Основным уравнением молекулярно кинетической теории идеального газа называется уравнение связывающее давление, оказываемое идеальным газом на стенки сосуда с характеристиками его молекул: (m0 – масса молекулы газа; Средняя кинетическая энергия поступательного движения одной молекулы идеального газа пропорциональна термодинамической температуре и зависит только от нее. Более детальное описание системы заключается в определении не только средней скорости, но и закона распределения молекул по скоростям. Этот закон теоретически выведен Максвеллом. Закон Максвелла описывается некоторой функцией f(), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, то на каждый интервал скорости будет приходиться некоторое число молекул dN(), имеющих скорости в интервале от до +d , пропорциональное ширине интервала d. Таким образом, функция f() определяет относительное число молекул Г 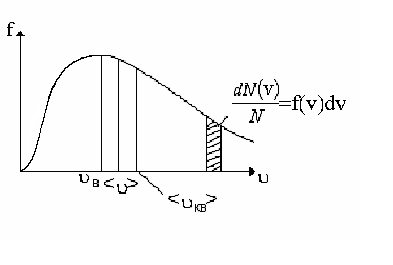 рафик функции представляет собой немонотонную кривую обращающуюся в ноль при = 0 и = . При увеличении температуры максимум функции распределения становится более пологим и смещается в область больших скоростей. Скорость при которой достигается максимум функции распределения называется наиболее вероятной скоростью В. Этой скоростью и близкой к ней обладает наибольшее число молекул. Кривая несимметрична относительно В. Расчеты показывают, что рафик функции представляет собой немонотонную кривую обращающуюся в ноль при = 0 и = . При увеличении температуры максимум функции распределения становится более пологим и смещается в область больших скоростей. Скорость при которой достигается максимум функции распределения называется наиболее вероятной скоростью В. Этой скоростью и близкой к ней обладает наибольшее число молекул. Кривая несимметрична относительно В. Расчеты показывают, чтоС помощью функции распределения можно установить среднее значение любой величины X зависящей от скорости Например, среднее значение скорости  , ,среднее значение квадрата скорости 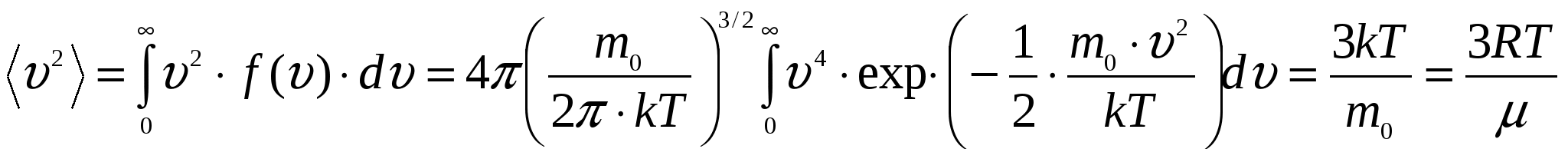 . .Если газ находится в поле внешних сил, то кроме распределения по скоростям устанавливается распределение по координатам. В случае поля тяготения Земли это приводит к тому, что концентрация молекул и давление газа изменяются с высотой. Закон изменения установлен Больцманом для изотермической атмосферы: 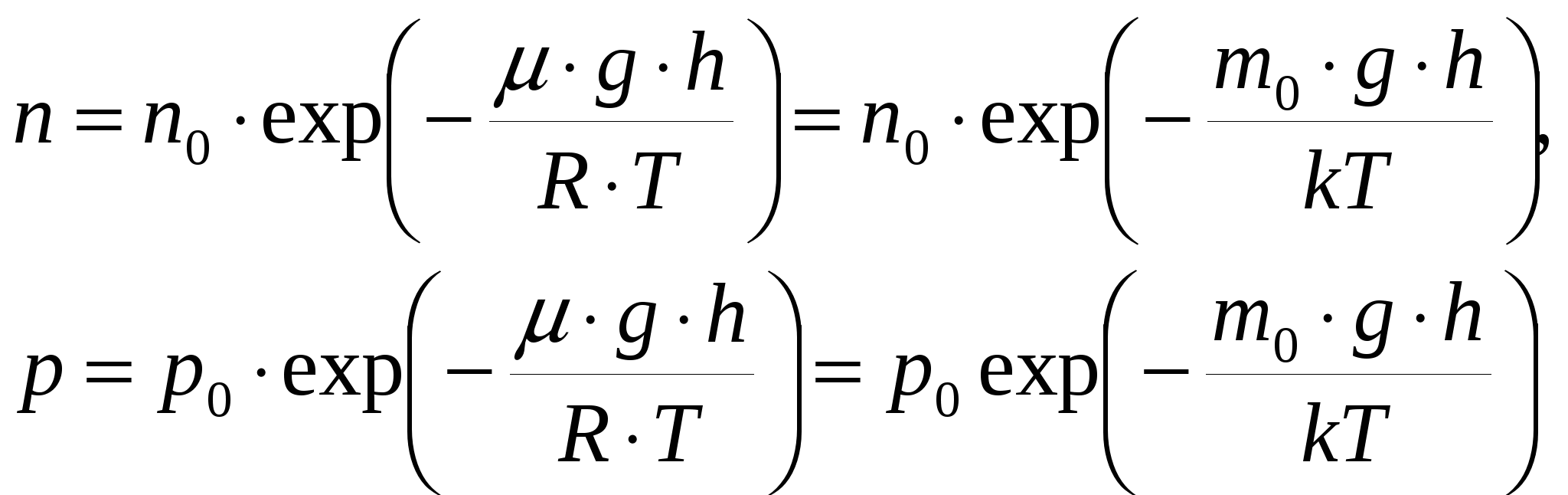 где p0 и n0-давление и концентрация молекул на высоте h = 0. Первая из формул называется распределением Больцмана, вторая - барометрической формулой. Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь , который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, поэтому можно говорить о средней длине свободного пробега молекул < >. За единицу времени молекула проходит путь, равный <> и, если (d эффективный диаметр молекулы). В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии (теплопроводность), массы (диффузия), импульса (внутреннее трение). Уравнения, описывающие явления переноса называются:
(
(
( Знак минус в уравнениях показывает, что перенос энергии, массы и импульса идет в направлении противоположном направлению возрастания температуры, плотности и скорости соответственно. Коэффициенты , D и связаны простыми соотношениями: Примеры решения задач Задача № 1 В сосуде объёмом V = 1 л находится углекислый газ массой m = 0,2 г. При температуре T =2600 K некоторая часть молекул диссоциировала на молекулы кислорода и окиси углерода. При этом давление газа в сосуде оказалось равным 108 кПа. Определить какая часть молекул диссоциировала.
Рассмотрим уравнение диссоциации углекислого газа Таким образом, каждый моль углекислого газа, распадаясь вызывает появление одного моля окисла углерода и половину моля кислорода. В результате распада части молекул в сосуде будут находиться три газа: CO2, CO, O2. По закону Дальтона найдём выражение для давления, создаваемого данной смесью газов Введём степень диссоциации число молей CO число молей O2 (с учётом уравнения реакции) И Общее давление будет связано со степенью диссоциации Так как Ответ: степень диссоциации газа = 0,2. Задача № 2 Используя функцию распределения Максвелла по скоростям, найдите наиболее вероятное значение кинетической энергии атомов гелия, который при давлении P = 105 Па имеет плотность =160 г/м3.
Запишем функцию распределения Максвелла по скоростям. Поскольку нужно найти наиболее вероятное значение энергии, имеет смысл перейти от распределения по скоростям к распределению по энергиям f( Из данного выражения можно получить соотношение связывающее две функции распределения: 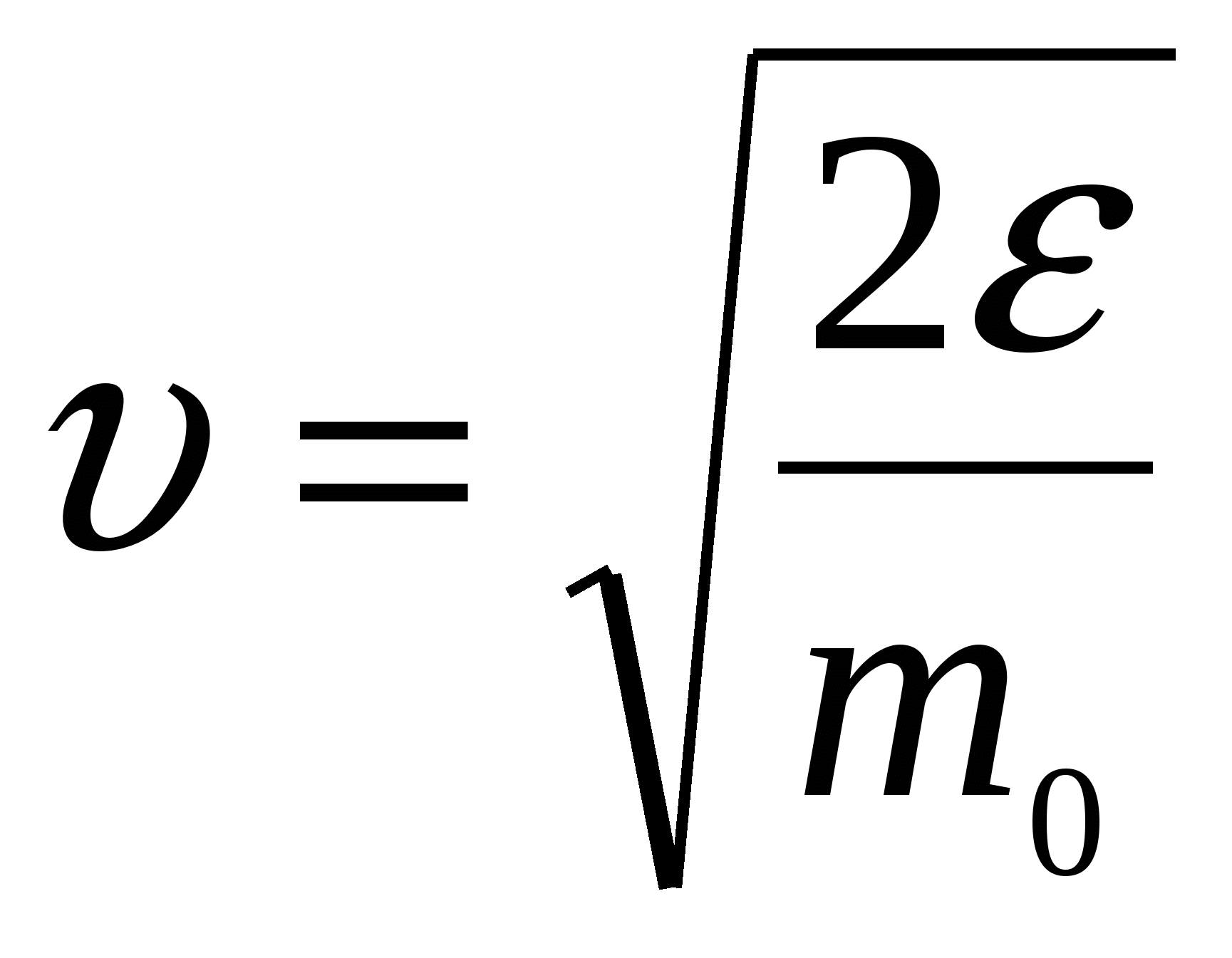 , то производная , то производная 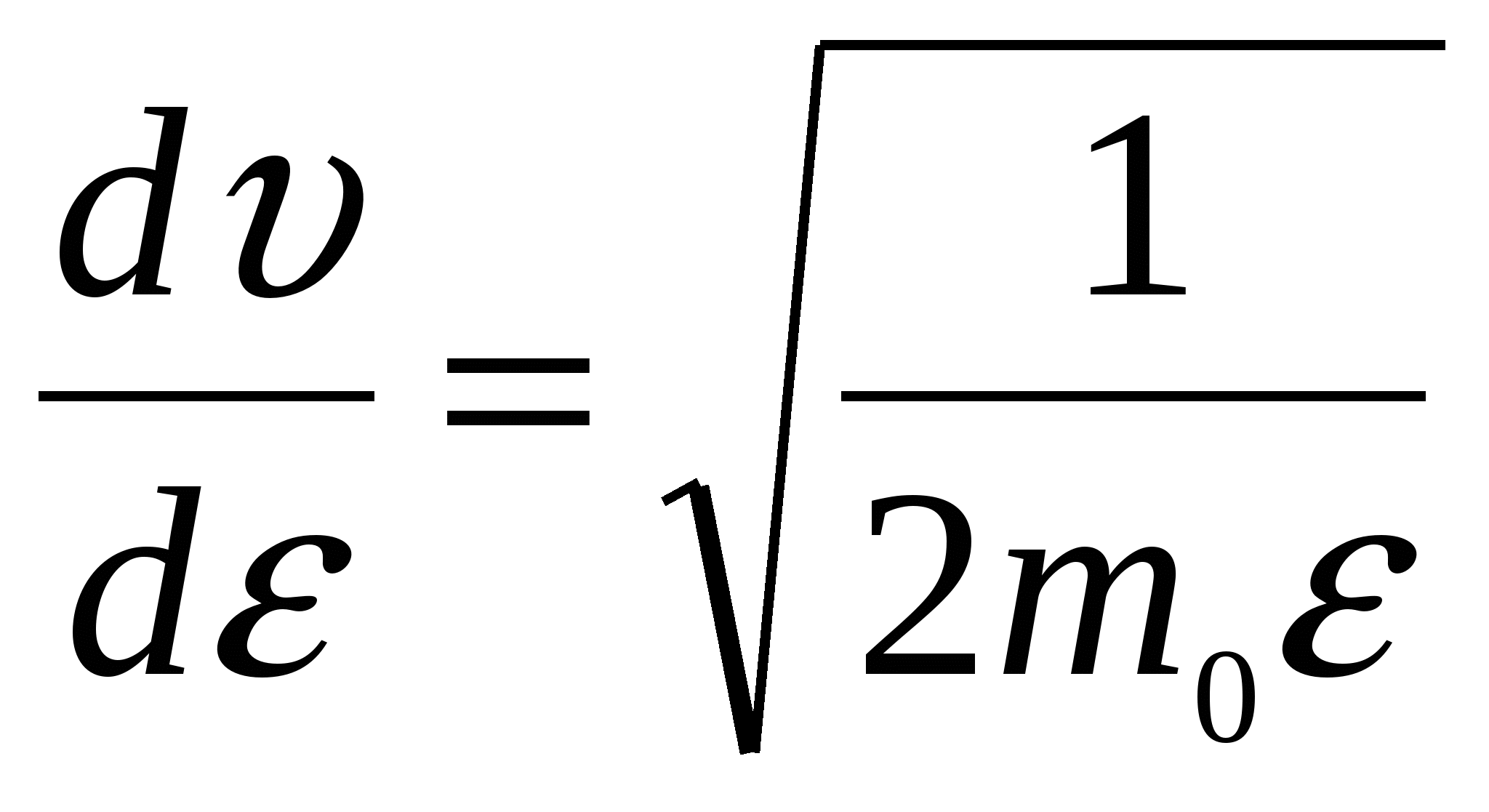 , и выражения для распределения по энергиям будет иметь вид. , и выражения для распределения по энергиям будет иметь вид.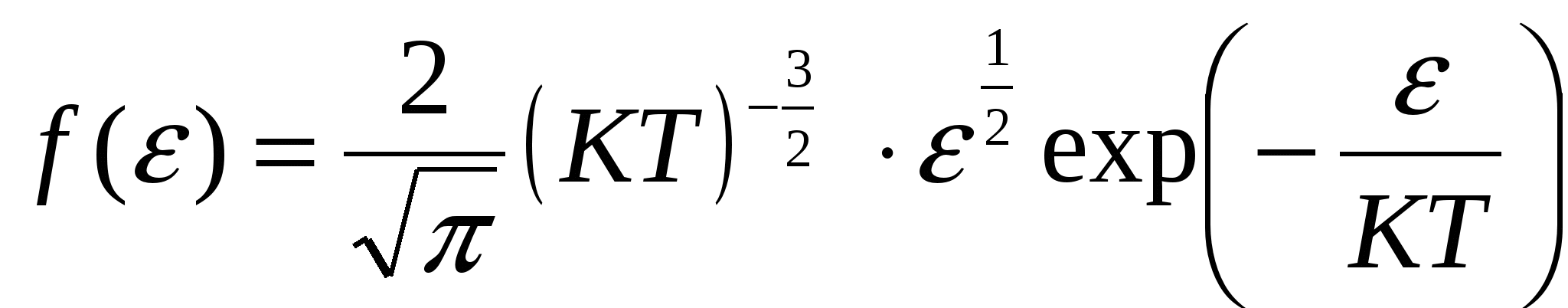 . .Наиболее вероятное значение энергии 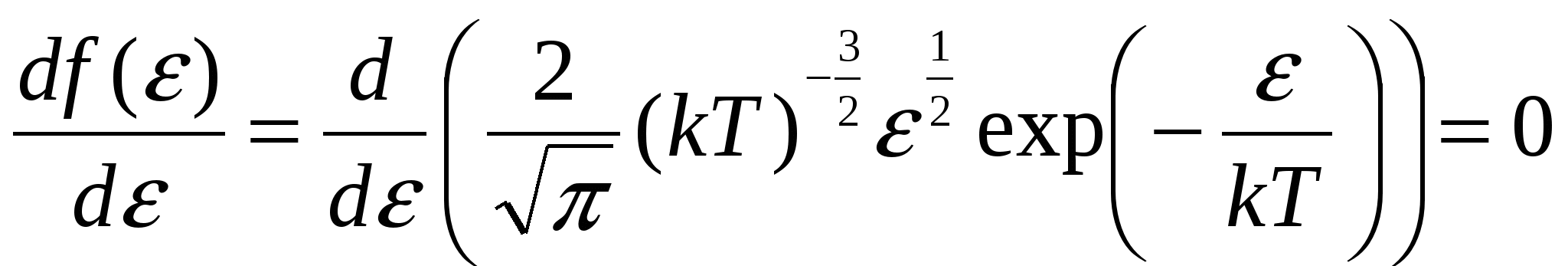 , ,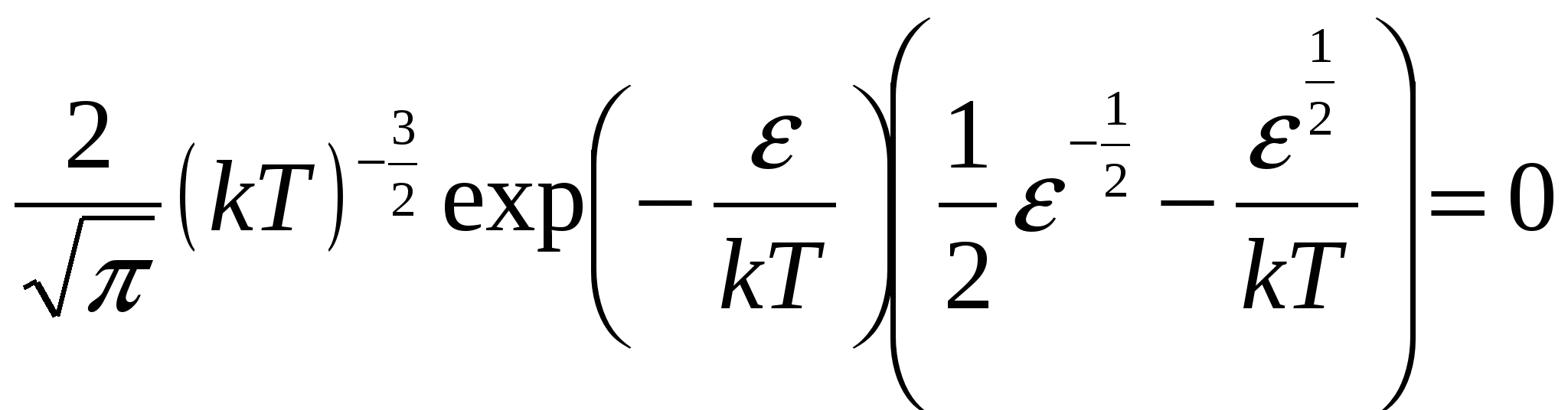 , ,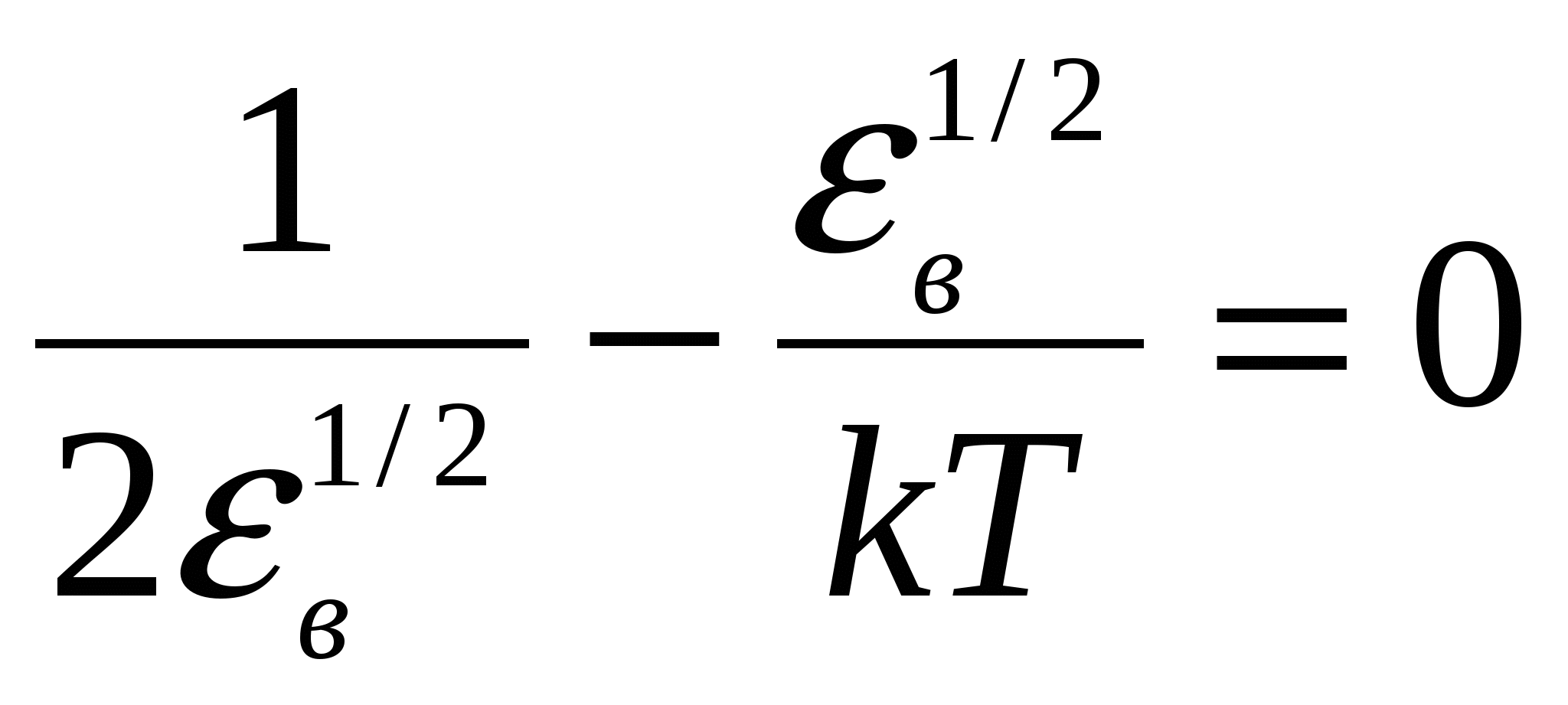 , , Обращаем внимание, что выражение для наиболее вероятной энергии нельзя получить подставив в формулу Из уравнения МенделееваКлапейрона следует, что (в последней формуле учтено, что R = NA·k). Подставляя данные из условия и молярную массу гелия Ответ: наиболее вероятное значение кинетической энергии атома гелия Задача № 3 Ротор центрифуги, заполненный радоном, вращается с частотой |
