Итоговый. Методические указания по решению задач Омск 2004 Составители Ласица Александр Михайлович Кондратьева Тамара Николаевна

• Название: Методические указания по решению задач Омск 2004 Составители Ласица Александр Михайлович Кондратьева Тамара Николаевна
• Анкор: Итоговый.doc
• Дата: 01.12.2017
• Размер: 2.6 Mb.
• Имя файла: Итоговый.doc
• Тип: Методические указания; #10576
• Категория: Физика
• страница: 3 из 4

V занимает смесь азота массой m₁ = 1 кг и гелия m₂ = 1 кг при нормальных условиях – давлении 760 мм рт. ст. и температуре 273 К?

Один баллон емкостью V₁ = 20 л содержит азот под давлением P₁ = 24 атм, другой – емкостью V₂ = 44 л содержит кислород под давлением P₂ = 16 атм. Оба баллона были соединены между собой и оба газа смешались, образовав однородную смесь (без изменения температуры). Найти парциальные давления P₁ и P₂ обоих газов в смеси и полное давление Р.

В сосуде при температуре t = 100 ⁰С и давлении P = 4ּ10⁵ Па находится 2 м³ смеси кислорода и сернистого газа SO₂. Определить парциальные давления компонентов, если масса сернистого газа т₂ = 9 кг.

Три баллона емкостью 3 л, 7 л и 5 л наполнены соответственно кислородом (2 атм), азотом (3 атм) и углекислым газом (0,6 атм) при одной и той же температуре. Баллоны соединяют между собой, причем образуется смесь той же температуры. Каково давление смеси?

Газовая смесь, состоящая из кислорода и азота, находится в баллоне под давлением P = 720 мм рт. ст. Считая, что масса кислорода составляет 40 % от массы смеси, определить концентрацию молекул отдельных газов при температуре 290 К.

Зная функцию распределения молекул по скорости, вывести формулу наиболее вероятной скорости.

Используя функцию распределения молекул по скорости, получить функцию, выражающую распределение молекул по относительным скоростям u (u = υ/υ_в).

Определить относительное число молекул идеального газа, скорости которых заключены в пределах от нуля до одной сотой наиболее вероятной скорости.

Какая часть молекул азота при 150 ⁰С обладает скоростями от 300 до 325 м/с?

Какая часть молекул кислорода при 0⁰С обладает скоростью от 100 до 110 м/с?

Какая часть молекул азота, находящегося при температуре Т, имеет скорости, лежащие в интервале от υ_в до υ_в +∆υ, где ∆υ = 20 м/с, Т = 400 К.

Определить температуру кислорода для которой функция распределения по скоростям будет иметь максимум при скорости υ = 420 м/с.

Определить температуру водорода, при которой средняя квадратичная скорость молекул больше их наиболее вероятной скорости на ∆υ = 400 м/с.

Во сколько раз средняя квадратичная скорость молекул водорода больше средней квадратичной скорости молекул водяных паров при той же температуре?

Азот находится под давлением p = 10⁵ Па при температуре Т =300 К. Найти относительное число молекул азота, скорости которых лежат в интервале от υ_в до υ_в +∆υ, где ∆υ = 1 м/с.

Зная функцию распределения молекул по скоростям, определить среднюю арифметическую скорость <υ> молекул.

По функции распределения молекул по скоростям определить среднюю квадратичную скорость <υ_кв.>.

Найти среднюю арифметическую, среднюю квадратичную и наиболее вероятную скорости молекул газа, плотность которого при давлении 300 мм рт. ст. равна 0,3 г/л.

При какой температуре средняя квадратичная скорость молекул азота больше их наиболее вероятной скорости на 50 м/с?

Какая часть общего числа N молекул имеет скорости: 1) больше наиболее вероятной скорости и 2) меньше наиболее вероятной скорости?

Пылинки, взвешенные в воздухе, имеют массу m = 10^-18 г. Во сколько раз уменьшится их концентрация n при увеличении высоты на ∆h =10 м? Температура воздуха Т = 300 К.

Масса т каждой из пылинок, взвешенных в воздухе, равна 1 аг. Отношение концентрации n₁ пылинок на высоте h₁ = 1 м к концентрации п₀их на высоте h₀= 0 равно 0,787. Температура воздуха Т = 300 К. Найти по этим данным значение постоянной Авогадро N_A.

Насколько уменьшится атмосферное давление p= 100 кПа при подъеме наблюдателя над поверхностью Земли на высоту h= 100 м? Считать, что температура Т воздуха равна 290 К и не изменяется с высотой.

На какой высоте h над поверхностью Земли атмосферное давление вдвое меньше, чем на её поверхности? Считать, что температура Т воздуха равна 290 К и не изменяется с высотой.

Барометр в кабине летящего вертолета показывает давление p = 90 кПа. На какой высоте h летит вертолет, если на взлетной площадке барометр показывал давление p₀ = 100 кПа? Считать, что температура Т воздуха равна 290 К и не изменяется с высотой.

Найти изменение высоты ∆h, соответствующее изменению давления на ∆p= 100 Па, в двух случаях: 1) вблизи поверхности Земли, где температура T₁= 290 К, давление p₁ = 100 кПа; 2) на некоторой высоте, где температура Т₂ = 220 К, давление p₂ = 25 кПа.

Барометр в кабине летящего самолета все время показывает одинаковое давление p = 80 кПа, благодаря чему летчик считает высоту h полета неизменной. Однако температура воздуха изменилась на ∆Т = 1 К. Какую ошибку ∆h в определении высоты допустил летчик? Считать, что температура не зависит от высоты и что у поверхности Земли давление p₀ = 100 кПа.

Высотная космическая станция расположена на горе Алагез в Армении на высоте 3250 м над уровнем моря. Найти давление воздуха на этой высоте. Температуру воздуха считать постоянной и равной 5⁰С. Массу одного киломоля воздуха принять равной 29 кг/моль. Давление воздуха на уровне моря равно 760 мм рт. ст.

На какой высоте давление воздуха составляет 75 % от давления на уровне моря? Температуру считать постоянной и равной 0 ⁰С.

Пассажирский самолет совершает полеты на высоте 8300 м. чтобы не снабжать пассажиров кислородными масками, в кабинах при помощи компрессора поддерживается постоянное давление, соответствующее высоте 2700 м. Найти разность давлений внутри и снаружи кабины. Среднюю температуру наружного воздуха считать равной 0 ⁰С.

Найти в предыдущей задаче, во сколько раз плотность воздуха в кабине больше плотности воздуха вне её, если температура наружного пространства равна минус 20⁰С и температура внутри кабины 20⁰С.

Какова масса 1 м³ воздуха: 1) у поверхности Земли, 2) на высоте 4км от поверхности Земли? Температуру воздуха считать постоянной и равной 0⁰С. Давление воздуха у поверхности Земли равно 10⁵ Па.

На какой высоте плотность газа составляет 50 % от его плотности на уровне моря? Температуру считать постоянной и равной 0 ⁰С. Задачу решить для: 1) воздуха и 2) водорода.

На поверхности Земли барометр показывает 101 кПа. Каково будет давление при подъеме барометра на высоту 540 м. Температуру считать одинаковой и равной 7 ⁰С.

Определить высоту горы, если давление на её вершине равно половине давления на уровне моря. Температура всюду одинакова и равна 0 ⁰С.

Найти количество азота, прошедшего вследствие диффузии через площадку 10 см² за 5 с, если градиент плотности азота в направлении, перпендикулярном площадке, 1,26 мг/см⁴. Коэффициент диффузии 1,42 см²/с.

За какое время 720 мг углекислого газа продиффундируют из почвы в атмосферу через 1 м² её поверхности при градиенте плотности 500 мг/см⁴? Коэффициент диффузии принять равным 1,42 см²/с.

Определить динамическую вязкость кислорода при нормальных условиях. Принять среднюю длину свободного пробега молекул 100 нм.

При некоторых условиях длина свободного пробега молекул водорода равна 0,5 мкм. Определить диаметр молекулы, если эти условия таковы: давление 0,2 МПа, температура 17 ⁰С.

Найти количество азота, прошедшего вследствие диффузии через площадку 100 см² за 10 с, если градиент плотности в направлении, перпендикулярном к площадке, равен 1,26 кг/м⁴.

Коэффициенты диффузии и внутреннего трения кислорода при некоторых условиях соответствуют 0,12 Мм²/с и 19,5 мкПаּс. Найти при этих условиях плотность кислорода.

В сосуде объемом 2 л находится 4,0ּ10²² молекул двухатомного газа. Коэффициент диффузии равен 2,0ּ10^-5 м²/с. Определить коэффициент теплопроводности газа при этих условиях.

Какой толщины следовало бы сделать деревянную стену здания, чтобы она давала такую же потерю теплоты, как кирпичная стена толщиной 40 см при одинаковых температурах внутри и снаружи здания? Коэффициенты теплопроводности кирпича и дерева равны соответственно 0,70 и 0,175 Вт/(мּК).

Между двумя пластинками, находящимися на расстоянии 1 мм друг от друга, находится воздух. Между пластинками поддерживается разность температур 1⁰С. Площадь каждой пластины равна 100 см². Какое количество тепла передается за счет теплопроводности от одной пластины к другой за 10 мин? Считать, что воздух находится при нормальных условиях. Диаметр молекулы равен 0,3 нм.

Найти коэффициент теплопроводности водорода, если известно, что коэффициент внутреннего трения для него при этих условиях 8,6 мкПаּс.

Средняя длина свободного пробега молекулы углекислого газа при нормальных условиях равна 50 нм. Определить среднюю арифметическую скорость молекулы и число соударений, которое испытывает молекула. d = 0,7 нм.

В колбе объемом 100 см³ находится 0,5 г азота. Найти среднюю длину свободного пробега молекул азота при этих условиях, d= 0,3 нм.

В сосуде объемом 0,5 л находится кислород при нормальных условиях. Найти общее число столкновений между молекулами кислорода за одну минуту. d = 0,3 нм.

Найти среднее время между двумя последовательными столкновениями молекул азота при температуре 10 ⁰С и давлении 1 мм рт. ст. d = 0,3 нм.

Какое предельное число молекул газа должно находиться в 1 см³ сферического сосуда диаметром 15 см, чтобы молекулы не сталкивались друг с другом? Диаметр молекулы газа принять равным 0,3 нм.

Как изменится число ударов молекул одноатомного газа о стенку баллона площадью 1м² за 1 с, если давление газа увеличится в 4 раза в 1) изотермическом и 2) изохорном процессах?

При каком давлении средняя длина свободного пробега молекул азота равна 1 мм, если при нормальном давлении она равна 8ּ10^-6 см?d = 0,3 нм.

Плотность фотосферы, оцениваемая оптическими методами, составляет 2ּ10^-4кг/м³. Определить длину свободного пробега атомов водорода в фотосфере, d = 0,23 нм.

В сосуде вместимостью 1 дм³ находится азот при температуре 7 ⁰С и давлении 0,2 МПа. Определить число столкновений молекул азота в этом сосуде за 1с, d = 0,3 нм.

Какое давление нужно создать в колбе диаметром 0,1 м, содержащей азот при температуре 20 ⁰С, чтобы получить вакуум? d = 0,3 нм.

Средняя длина свободного пробега молекул водорода при некотором давлении и температуре 21 ⁰С равна 90 нм. В результате изотермического процесса давление газа увеличилось в 3 раза. Найти среднее число столкновений молекул водорода за 1 с в конце процесса. d = 0,23 нм.

При каком давлении средняя длина свободного пробега молекул водорода равна <λ> = 2,5 см? Температура t =68 ⁰С, d = 0,23 нм.

В баллоне вместимостью 10 дм³ находится гелий массой 2 г. Определить среднюю длину свободного пробега молекул гелия, d = 0,2 нм.

Средняя длина свободного пробега молекул гелия при нормальных условиях 230 нм. Найти среднюю продолжительность свободного пробега молекул гелия при давлении 1,0 МПа и температуре 17 ⁰С, d = 0,2 нм.

В сферическом сосуде вместимостью 2 дм³ находится водород. При какой плотности водорода молекулы его практически не будут сталкиваться друг с другом? d = 0,23 нм.

Определить коэффициент диффузии двухатомного газа, находящегося в сосуде объемом 2,0 л с числом молекул 4,0ּ10²², если коэффициент теплопроводности этого газа 144 мВт/(мּК).

Определить среднюю длину свободного пробега молекул кислорода, если при температуре 0 ⁰С коэффициент диффузии кислорода 0,20 см²/с, d = 0,3 нм.

Найти коэффициент теплопроводности водорода, если коэффициент вязкости для него при этих условиях 8,6 мкПаּс.

Определить коэффициент диффузии гелия, если средняя длина свободного пробега атомов гелия при нормальных условиях 180 нм.

Углекислый газ и азот находятся при одинаковых температурах и давлениях. Найти для этих газов отношение коэффициентов диффузии, внутреннего трения, теплопроводности. Диаметры молекул этих газов: d₁ = 0,4 нм, d₂ = 0,3 нм.


Основные положения термодинамики
Термодинамика – раздел физики, изучающий общие свойства макроско­пи­чес­ких систем и процессы перехода между различными состояниями. В основе термодинамики лежат установленные из опыта и подтверждающиеся всей совокупностью вытекающих из них следствий законы, называемые началами термодинамики.

Первое начало термодинамики по существу представляет собой закон сохранения энергии, примененный к термодинамическим процессам: количество теплоты, сообщенное термодинамической системе, идет на увеличение ее внутренней энергии U и совершение системой работы против внешних сил.

.

Для процессов, в которых термодинамические параметры системы меняются бесконечно мало можно записать первое начало в дифференциальной форме.

.

Под внутренней энергией системы подразумевают энергию этой системы за вычетом кинетической энергии системы как целого и потенциальной энергии системы в поле внешних сил. Внутренняя энергия, в отличие от работы и количества теплоты, является функцией состояния. Выражение для внутренней энергии предельно упрощается при рассмотрения простейшей термодинамической системы – идеального газа. В этом случае

.

где i- число степеней свободы молекул газа (i= 3 для одноатомного, i= 5 для двухатомного,i= 6 для многоатомного газа с жесткой связью между атомами в молекуле).

Элементарная работа, совершаемая газом против внешних сил при изменении его объема: 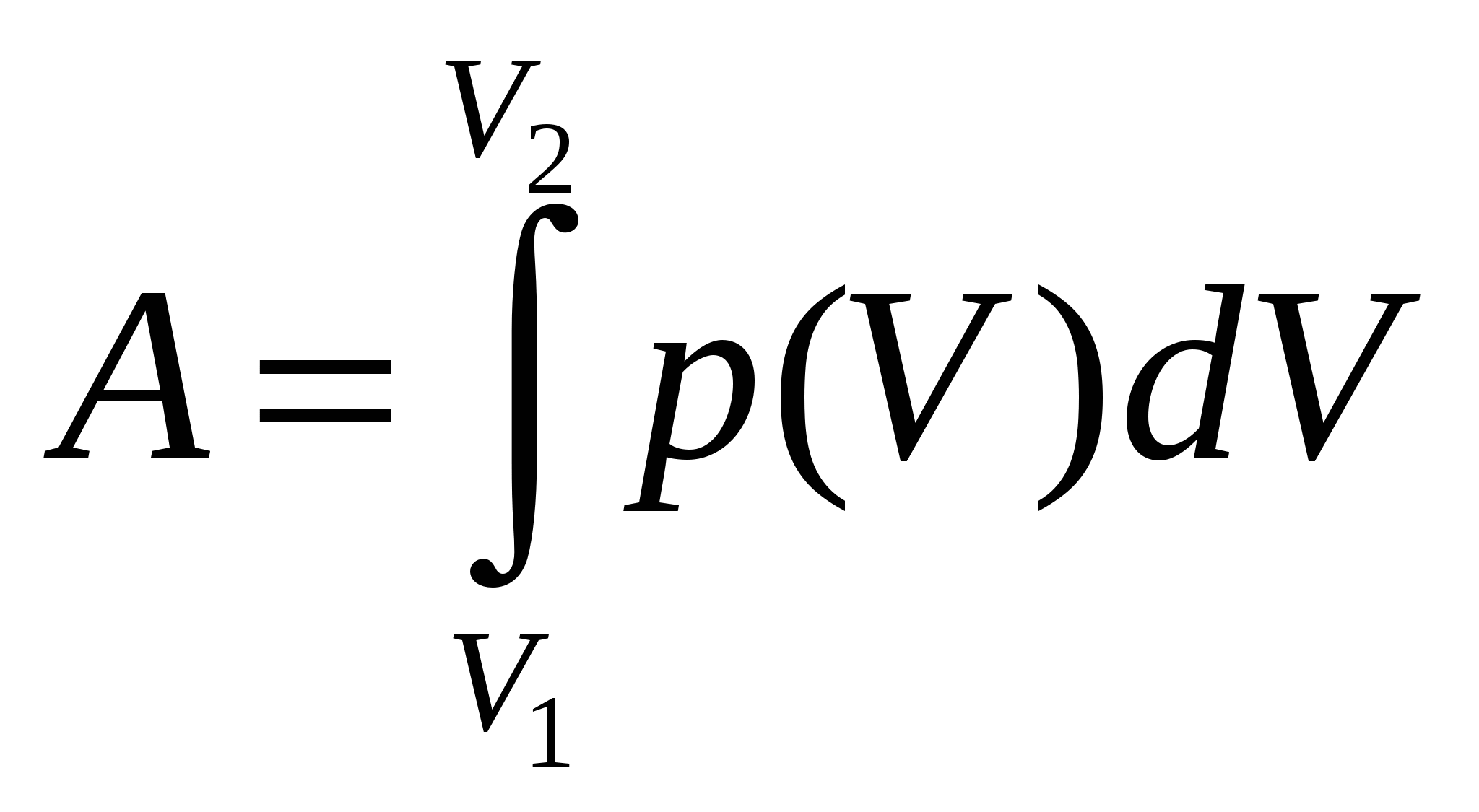. При изменении объема газа от V₁ до V₂ газ совершит работу

.

где p(V)  зависимость давления от объема в процессе расширения газа. Для изобарического процесса эта формула принимает вид

,

а для изотермического

.

Для расчета количества теплоты, переданного системе, вводится понятие теплоемкости – величины, равной количеству теплоты, не­об­хо­димому для нагревания вещества на 1 К: . Удобно ввести также удельную теплоемкость – величину, равную количеству теплоты, не­об­хо­димому для нагревания 1 кг вещества на 1 К: и молярную теплоемкость – величину, равную количеству теплоты, необходимому для нагревания одного моля вещества на 1 К: . Удельная теплоемкость связана с молярной соотношением .

Различают теплоемкости при постоянном давлении и постоянном объеме, если в процессе нагревания вещества поддерживается постоянным соответственно давление или объем. В случае нагревания при постоянном объеме не совершается работа против внешних сил, поэтому теплоемкость при постоянном объеме меньше теплоемкости при постоянном давлении. Применяя первое начало термодинамики, можно получить выражения для молярных теплоемкостей при постоянном объеме и давлении, а также уравнение связи между ними:



Последнее выражение называется уравнением Майера.

Адиабатическим называется процесс, происходящий без теплообмена с окружающей средой, при адиабатическом процессе давление, объем и температура газа связаны уравнениями Пуассона:

,

где 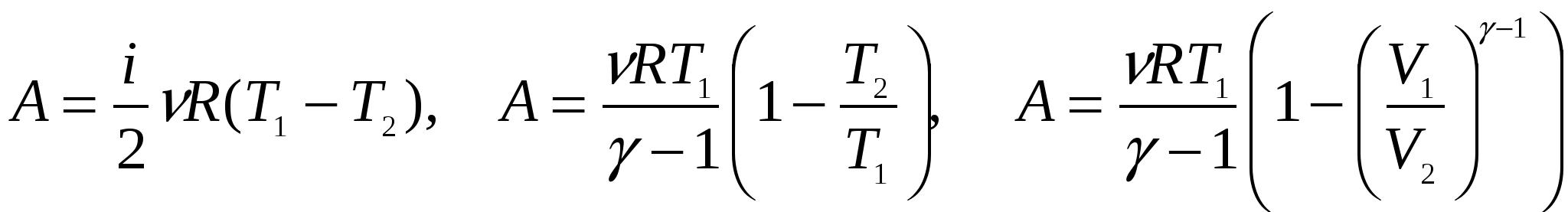 отношение теплоемкостей при постоянном давлении и объеме, которое называют показателем адиабаты или коэффициентом Пуассона. Работа в адиабатическом процессе совершается за счет убыли внутренней энергии и выражается следующими формулами:

.

Круговым процессом или циклом называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. Коэффициентом полезного действия тепловой машины называется выражение, определяемое формулами:

,

где А  работа, совершенная рабочим веществом тепловой машины за цикл, Q_Н  количество теплоты, полученное рабочим веществом от нагревателя, Q_Х  количество теплоты, отданное рабочим веществом холодильнику за то же время.

Второе начало термодинамики определяет направление протекания термодинамических процессов и может быть сформулировано несколькими эквивалентными способами. Наиболее часто встречаются формулировки Клаузиуса и Томсона: 1) невозможен процесс, единственным результатом которого является передача теплоты от холодного тела к горячему; 2) невозможен процесс, единственным результатом которого является совершение работы за счет охлаждения одного тела. Основываясь на втором начале термодинамики, Карно вывел теорему, носящую его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателя и холодильника, наибольшим КПД обладают обратимые машины; при этом КПД обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от конструкции машин. Введя в рассмотрение абстрактный обратимый цикл, состоящий из двух изотерм и двух адиабат, Карно установил формулу максимально возможного КПД тепловой машины 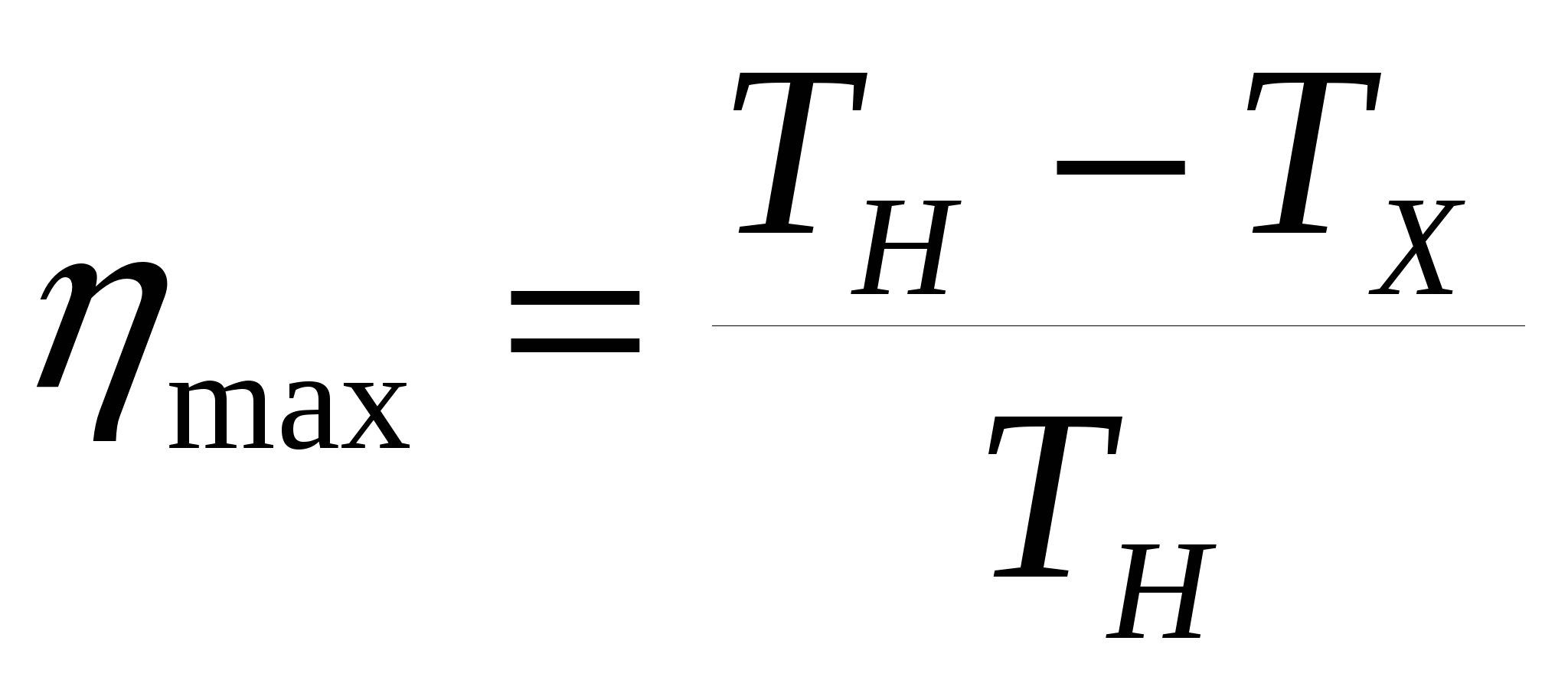(Т_Н, Т_Х  температуры нагревателя и холодильника).

Введя специальную функцию состояния системы  энтропию S, можно дать еще одну формулировку второго начала термодинамики: энтропия адиабатически изолированной системы при любых процессах, происходящих в ней, не уменьшается  она возрастает при необратимых процессах и остается постоянной при обратимых . Если система совершает переход из состояния 1 в состояние 2, то изменение энтропии

,

(знак равенства относится к обратимым процессам). Физический смысл энтропии раскрывает формула Больцмана , где k - постоянная Больцмана,W  термодинамическая вероятность состояния системы - число способов, которыми может быть реализовано данное состояние макросистемы.
Примеры решения задач
Задача № 1

Газ, занимавший объем 2 л при давлении 0,1 МПа, расширился изотермически до 4 л. После этого, охлаждая газ изохорически, уменьшили давление в 2 раза. Далее газ изобарически расширился до 8 л. Начертите график зависимости давления от объема, найдите работу, совершенную газом.

Дано: V1 = 2 л P1= 0,1 МПа V2 = 4 л P3 = V3 = 8 л

A - ?

Решение:

Построим график зависимости давления от объема. Первый процесс, происходящий с газом, является изотермическим. Выразим давление через объём и температуру при помощи уравнения Менделеева – Клапейрона . Так как T = const, давление в данном процессе обратно пропорционально объёму, и линия, изображающая данный процесс на p-V диаграмме, будет участком гиперболы начинающейся в точке V₁, p₁ и заканчивающейся в точке V₂, p₂.

Второй процесс, происходящий с газом, является изохорическим. В этом процессе объём не изменяется и, следовательно, на P-V диаграмме он изображается в виде вертикальной прямой, идущей из точки V₂, p₂ в точку V₂, p₃.

Третий процесс происходящий с газом, по условию задачи, изобарический. На P-V диаграмме он будет выглядеть как горизонтальная линия, идущая из точки V₂, p₃ в точку V₃, p_3.

П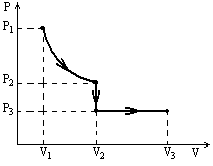оследовательно изображая все процессы, получим следующую P-V диаграмму.

Рассчитаем работу, совершенную газом. Так как работа, совершаемая газом,  аддитивная величина

А = А₁+А₂+А₃ ,

где А₁ – работа, совершенная в изотермическом процессе, А₂ – работа, совершенная в изохорическом процессе, А₃ – работа, совершенная в изобарическом процессе. Каждую из работ можно вычислить по формуле 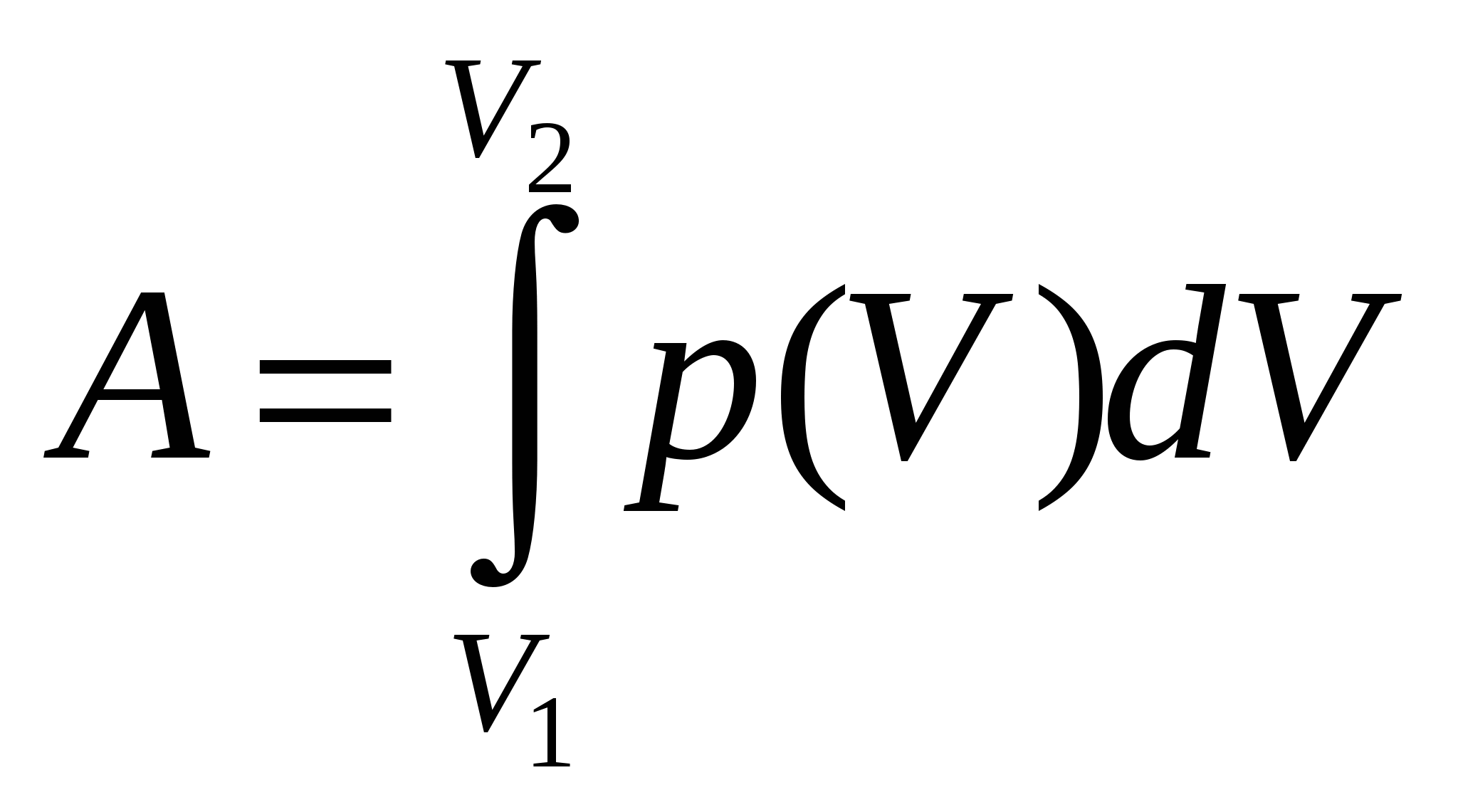(V₁ и V₂ – начальные и конечные объёмы занимаемые газом). Применим эту формулу для определения работы А₁. Согласно уравнению Менделеева – Клапейрона, зависимость p(V) имеет вид .

Следовательно, работа 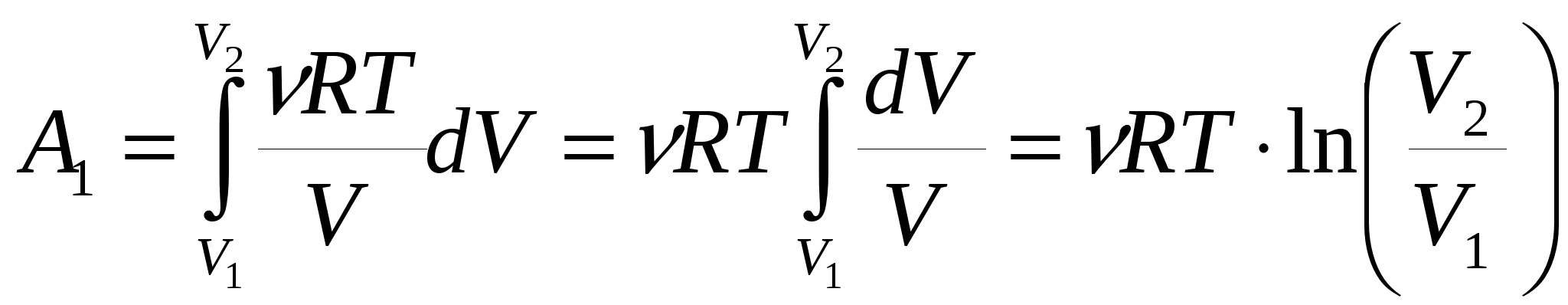. Множитель RT вынесем из-под знака интеграла как постоянную величину, заменяя её на p₁V₁, получим

.

В изохорическом процессе изменение объёма газа не происходит, следовательно, А₂ = 0.

При вычислении работы А₃ учтём, что давление, как постоянная величина, может быть вынесена из под знака интеграла
.

Для расчёта необходимо знать давление P₃. Так как первый процесс изотермический, . По условию задачи , следовательно,

.

Общая работа А = А₁+А₂+А₃ = 238,63 Дж.

Ответ: работа, совершенная газом А = 238,63 Дж.

В качестве дополнения заметим, что существует еще один способ определения работы, совершаемой газом, – графический. Как известно, площадь на диаграмме pV между линией, изображающей процессы, происходящие с газом, и осью объема по модулю равна работе. Если объём газа увеличится, то работа положительна, в противном случае  отрицательна. В ряде случаев этот метод позволяет найти работу, не прибегая к вычислению интегралов.

Задача № 2

Азот находящийся при температуре 400 К, подвергли адиабатическому расширению, в результате которого его объём увеличился в n = 5 раз, а внутренняя энергия уменьшилась на 4 кДж. Определите массу азота, считая его идеальным газом.

Дано: =28 г/моль i = 5 T1 = 400 K V2 = nV1 n = 5 ΔU = - 4 кДж

m -?

Решение:

Составим выражение изменения внутренней энергии азота, считая его идеальным газом.

ΔU = ΔT =

Учитывая, что процесс расширения происходил адиабатически, воспользуемся уравнением Пуассона, связывающим температуры и объёмы (-п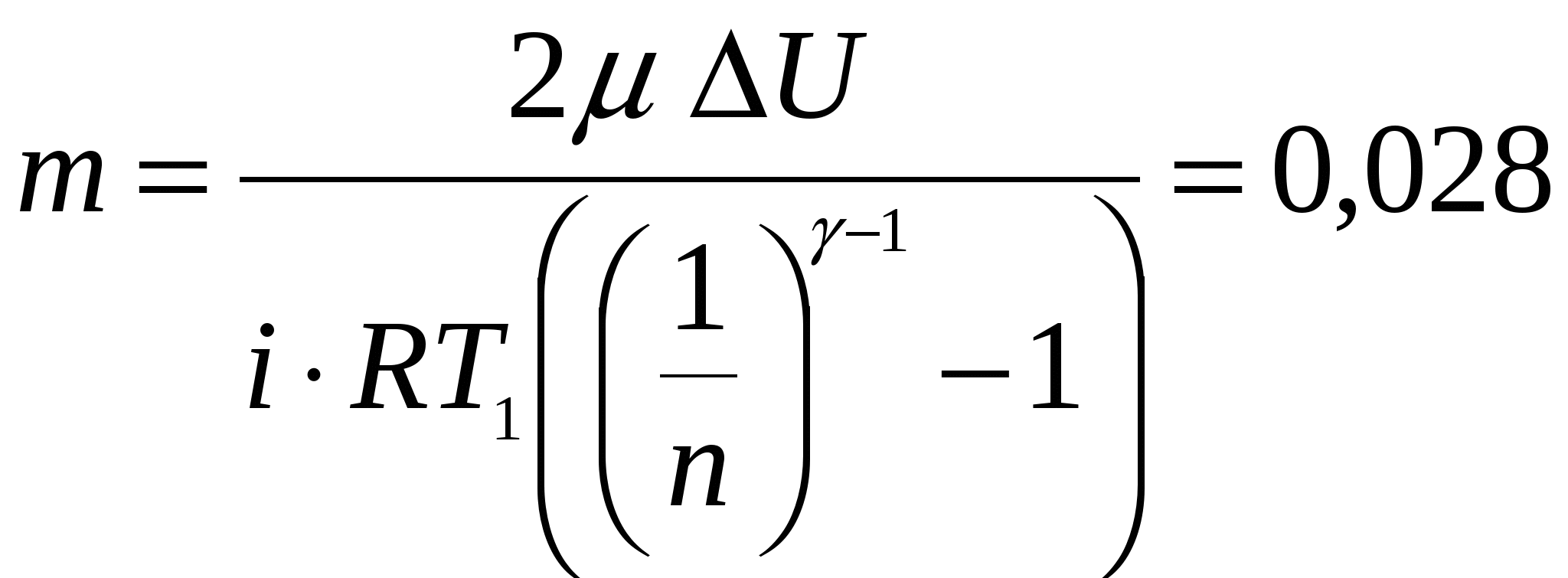оказатель адиабаты). С помощью данного уравнения сведём неизвестное отношение температур к известному отношению объёмов: .

Для изменения внутренней энергии в итоге получаем формулу .

Выразив массу и произведя расчеты, получим кг.
Ответ: масса азота m = 0.028 кг.

Задача № 3

Определите показатель адиабаты  для смеси газов, содержащей гелий массой = 8 г и водород массой = 2 г. Газы считать идеальными.

Дано: = 8г. 1= 4·10-3 кг/моль = 2г. 2 = 2·10-3 кг/моль

-?

Решение:

По определению . Рассчитаем удельные теплоёмкости для смеси газов. Первой вычислим теплоёмкость при постоянном объёме. Количество теплоты, необходимое для нагревания смеси газов на ΔT, с одной стороны, по определению теплоёмкости, равно .

С другой стороны, данное количество теплоты может быть представлено как сумма теплот, идущих на нагревание двух газов по отдельности:

.

Приравнивая выражения, получим .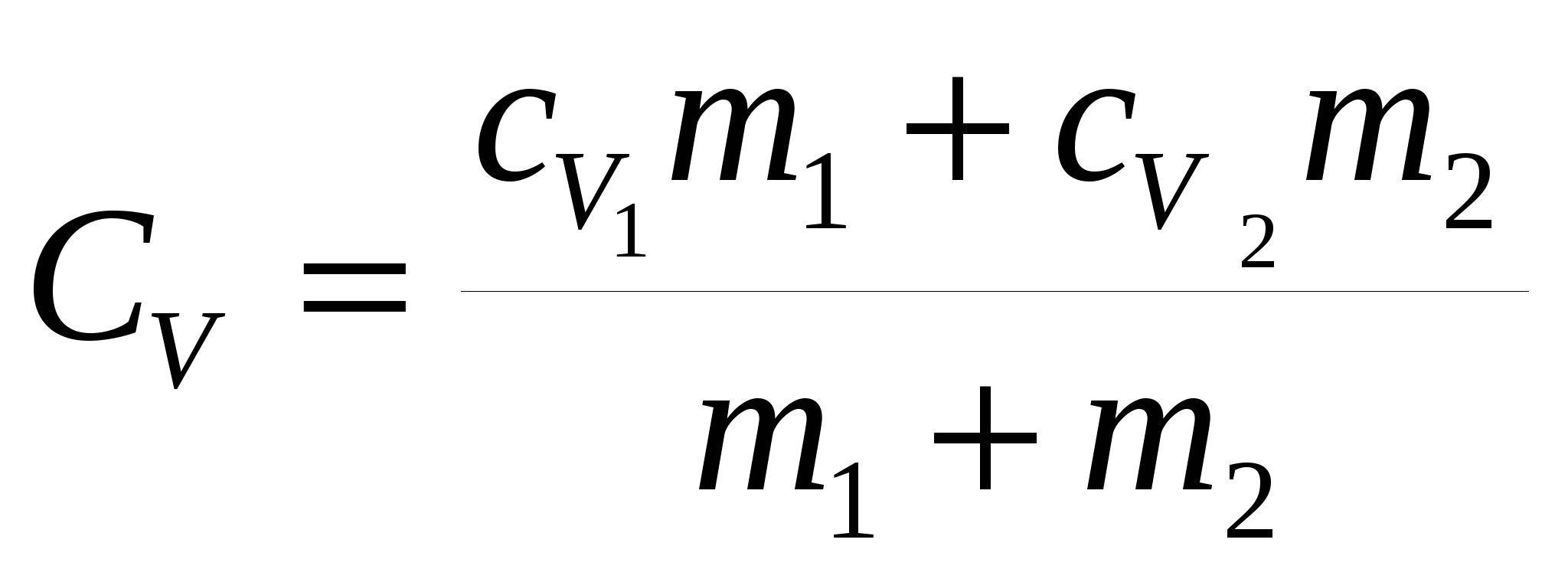

Удельные теплоёмкости газов можно выразить через число степеней свободы молекул и молярные массы газов:

; ,

где 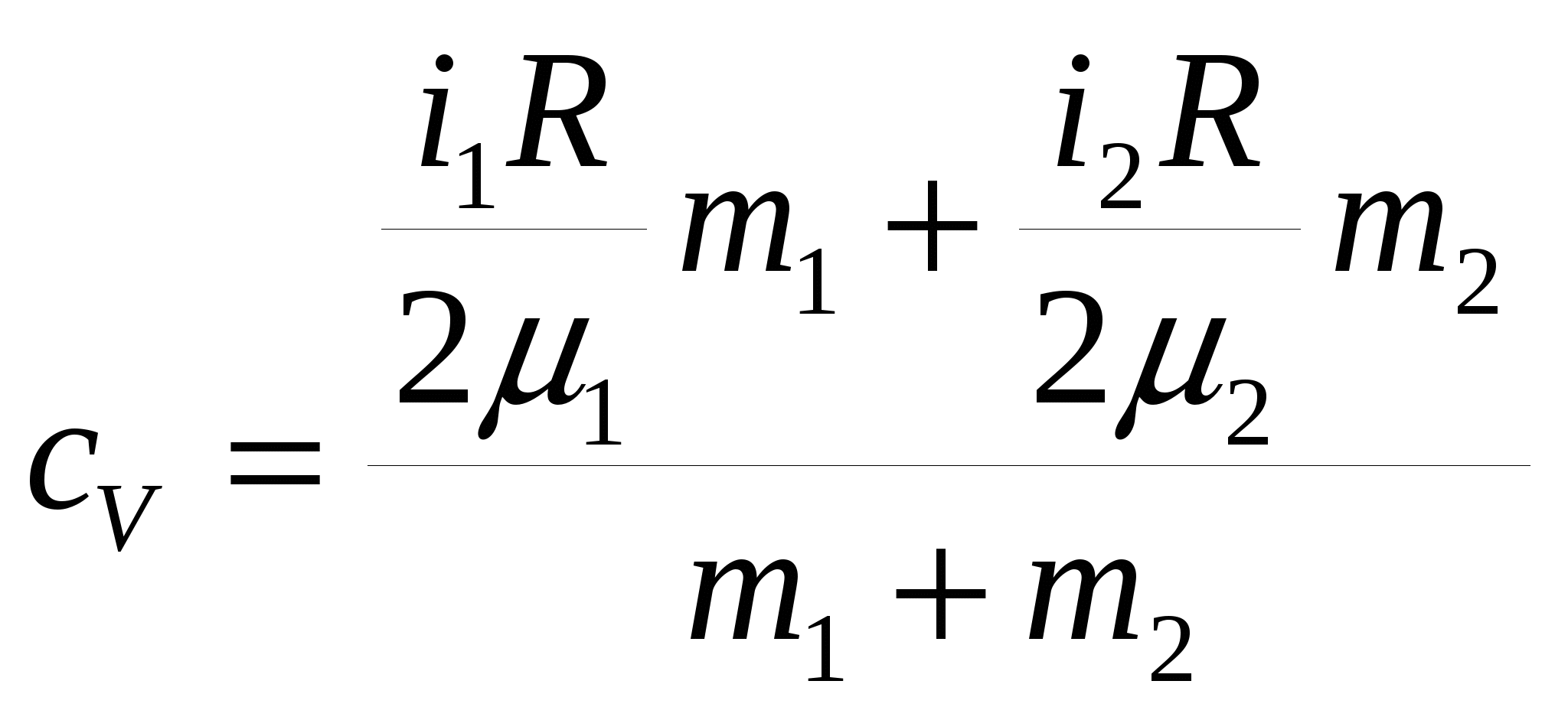= 3, = 5. После подстановки получаем

.

Аналогичные рассуждения дадут для удельной теплоёмкости при постоянном давлении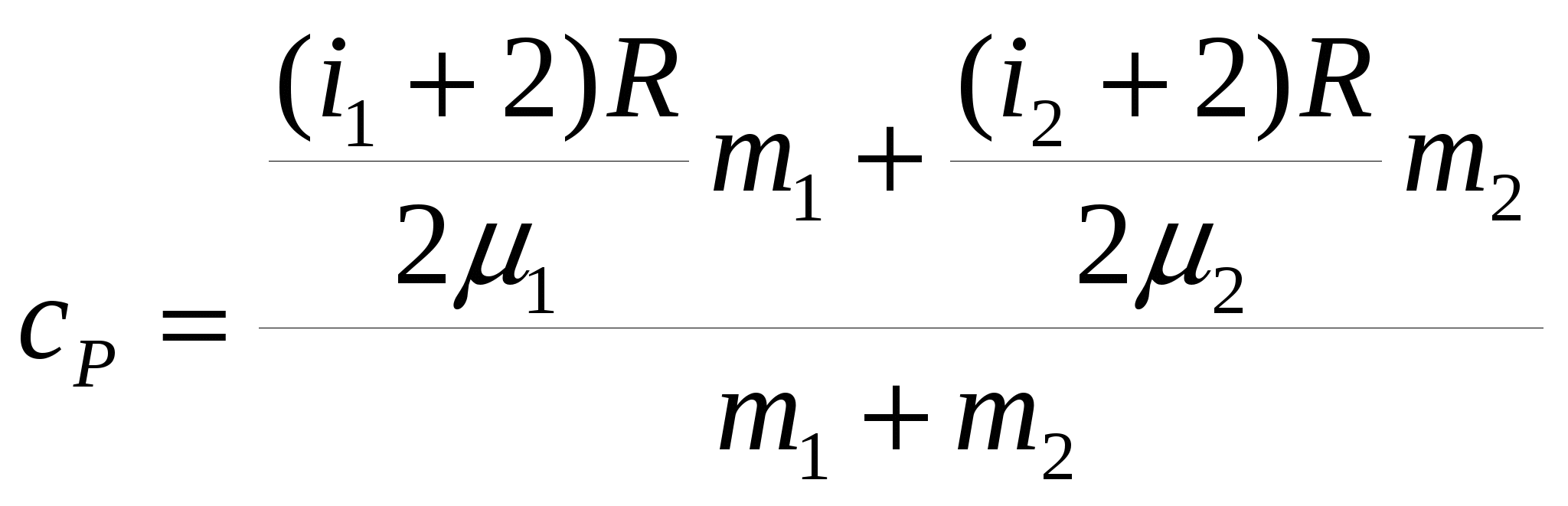

.

Соответственно, показатель адиабаты после подстановки полученных выражений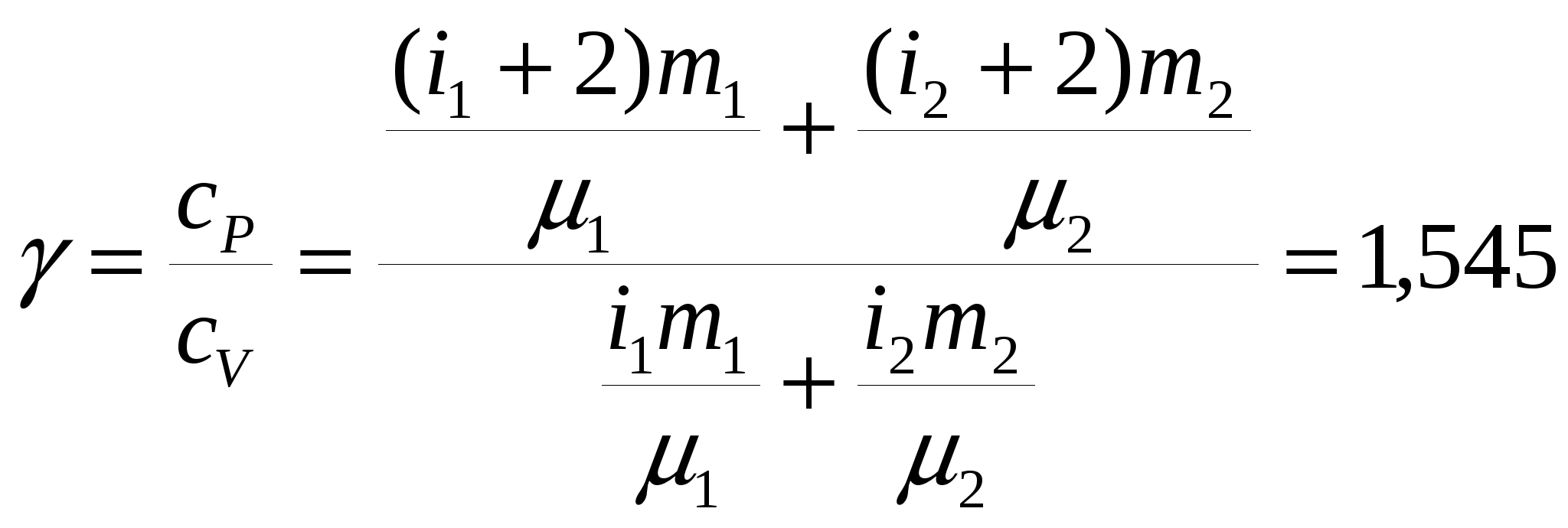

.

Ответ: показатель адиабаты .

З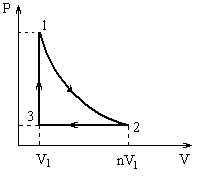адача № 4

Некоторая тепловая машина работает по циклу, состоящему из адиабаты, изобары и изохоры, изображенному на рисунке. Определить теоретический к. п. д. такого двигателя если степень сжатия (отношение максимального объёма к минимальному) n = 10, а в качестве рабочего тела используется идеальный двухатомный газ.

Дано: n = 10 i = 5

-?

Решение:

Теоретический КПД тепловой машины можно определить по формуле

.

Рассмотрим p-V диаграмму цикла, совершаемого тепловой машиной. На участке 1-2 машина не получает и не отдаёт теплоту, так как этот процесс адиабатический.

На участке 2-3 при постоянном давлении происходит уменьшение объёма, это возможно только в том случае, если уменьшаются температура газа, а следовательно, и его внутренняя энергия. Кроме того, работа, совершённая газом на этом участке, тоже отрицательна. Значит, согласно первому началу термодинамики (Q = A+ ΔU), отрицательным будет и количество теплоты, получаемой системой в данном процессе. Последнее означает, что процесс 2-3  это процесс, в котором система отдает теплоту холодильнику:

Q_X = ^- Q₂₃

(в формуле поставлен знак минус потому, что в выражении КПД стоят модули количеств теплоты, полученных и отданных тепловой машиной).

Рассмотрим участок 3-1: на данном участке при постоянном объёме увеличивается давление газа. Из уравнения Менделеева  Клапейрона следует, что увеличиваются температура газа и его внутренняя энергия. Так как работа в данном процессе не совершается (V = const), количество теплоты, полученное системой, равно изменению внутренней энергии и является положительной величиной - на участке 3-1 тело находится в контакте с нагревателем и

Q_H = Q₃₁.

С учётом всего вышесказанного можно преобразовать выражение КПД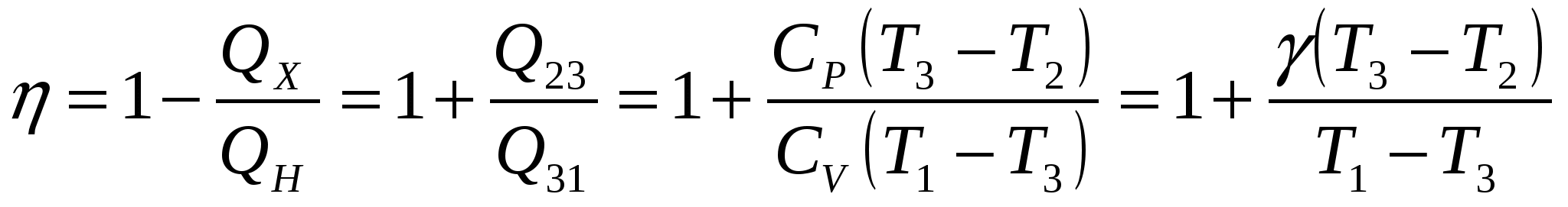

, где  показатель адиабаты.

Используя уравнение изобары, можно получить связь между температурами T₂ и T₃ = T₂/n.

Температуры в первом и во втором состояниях можно связать с помощью уравнения Пуассона: 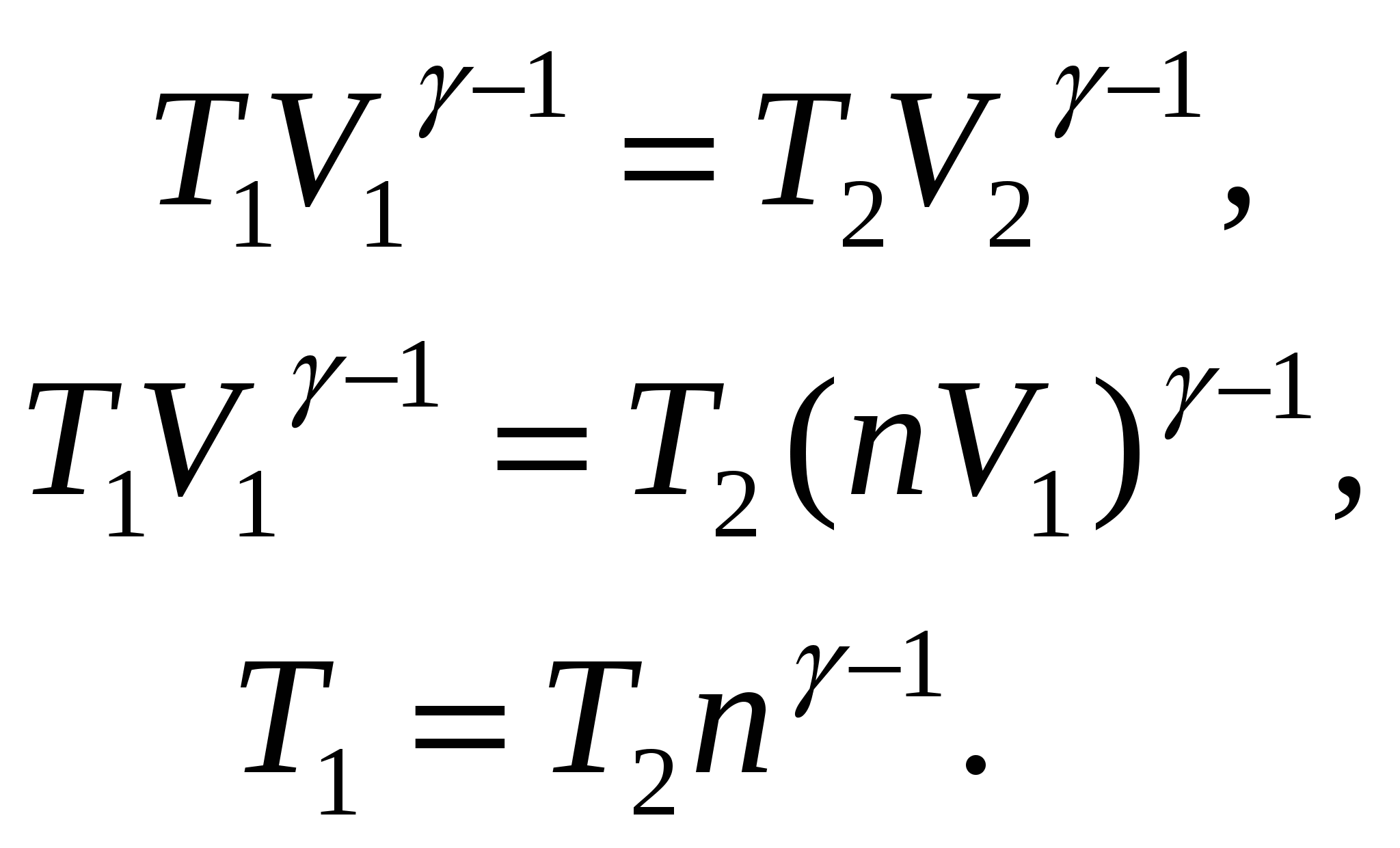. Применяя его к первому и второму состояниям, получим



Подставляя выражения для T₁ и T₃ в формулу КПД, получим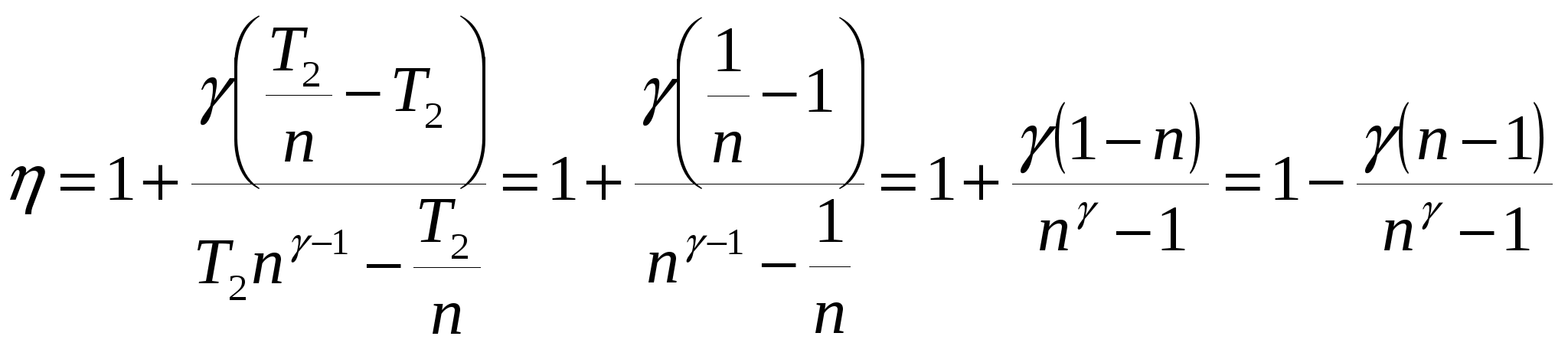

.

Учитывая, что для двухатомного газа i = 5 и , проводя расчёты, получим .

Ответ: .

Задача № 5

О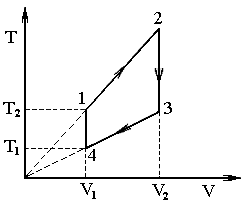пределить КПД тепловой машины, работающей по циклу, изображенному на рисунке, если известно, что V₂ = 2V₁, Т₂ = 2Т₁, а рабочим телом является идеальный трехатомный газ.

Дано: Т2 = 2Т1 V2 = 2V1

-?

Решение:

П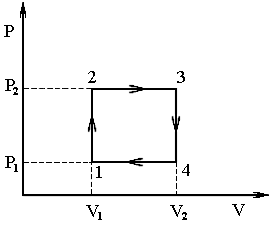режде всего проанализируем процессы, происходящие с газом. Процессы 2 – 3 и 4 – 1, как видно из рисунка, являются изохорическими. В процессах 1 – 2 и 3 – 4 температура прямо про­порциональна объёму. Значит, данные процессы являются изобарическими.

Перерисуем цикл машины в координатах p–V. По условию задачи температуры в начале и конце изохорического процесса отличаются в 2 раза. Значит, во столько же раз должны отличаться давления газа и можно записать, что p₂ = 2p₁.

КПД цикла, по определению, равен отношению работы, совершенной газом к количеству теплоты, полученной от нагревателя: .

Работа, совершаемая газом за цикл, численно равна площади, ограничиваемой циклом на диаграмме p-V. В данном случае эта площадь представляет собой прямоугольник, следовательно:

A = (p₂ - p₁)(V₂ - V₁) = p₁V₁.

Используя рассуждения, аналогичные приведенным в предыдущей задаче, можно прийти к выводу, что тело получает теплоту от нагревателя на участках 1-2 и 2-3 (на участках 3-4 и 4-1 рабочее тело тепловой машины отдаёт теплоту холодильнику): Q_н = Q₁₂ + Q₃₄.

Рассчитаем количество теплоты Q₁₂ = С_V(T₂ - T₁). С_V = 3R  молярная теплоемкость трёхатомного газа при постоянном объёме. Учтем, что для трёхатомного газа число степеней свободы i = 6. Т₁ и Т₂ температуры в соответствующих точках цикла. Раскрывая скобки и учитывая, что

RT₁ = p₁V₁; RT₂ = p₂V₁ = 2p₁V₁,

получим

Q₁₂ = 3R(T₂-T₁) = 3 (RT₂- RT₁) = 3(2p₁V₁ - p₁V₁) =3 p₁V₁.

Аналогично, можно записать Q₂₃ = С_p(T₃-T₂). С_р = 4R – молярная теплоёмкость трёхатомного идеального газа при постоянном объёме. Учитывая, что

RT₃ = p₂V₂ = 4p₁V₁,

запишем

Q₂₃ = 4R(T₃-T₂) = 4(4p₁V₁ – 2p₁V₁) = 8p₁V₁,

Q_Н = Q₁₂ + Q₂₃ = 11 p₁V₁.

Рассчитаем коэффициент полезного действия .

Ответ: .

Задача № 6

В двух сосудах одного и того же объёма находится гелий массой 10 г (₁= 4·10^-3 кг/моль) и азот массой 56 г (₂ = 28·10^-3 кг/моль). Давление и температура газов одинаковы. Сосуды соединяют и начинается процесс диффузии. Определить изменение энтропии системы в данном процессе.

Дано: m1 = 10 г 1= 4 г/моль m2 = 56 г 2=28 г/моль

ΔS -?

Решение:

Процесс диффузии в данной задаче можно рассматривать как процесс изотермического расширения. В этом случае изменениT энтропии гелия

.

Так как процесс изотермический, Q₁ = A₁. Вычисляя работу в изотермическом процессе, получим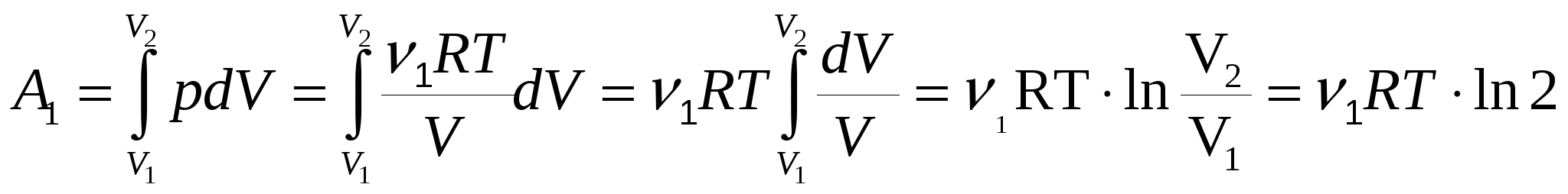

.

В последней формуле учтено, что V₂ = 2V₁, так как по условию объёмы обоих сосудов равны. Следовательно, .

Аналогичные вычисления для второго газа дают .

Полное изменение энтропии всей системы

.

Ответ: изменение энтропии системы в данном процессе .
Задачи, рекомендуемые для аудиторных занятий
1. Азот массой 5 кг, нагретый на 150 К, сохранил неизменный объем. Найти количество теплоты, сообщенное газу, изменение его внутренней энергии и совершенную газом работу.
2.Водород массой m = 4 г был нагрет на ∆T = 10 К при постоянном давлении. Определить работу расширения газа.
3. При изотермическом сжатии двух киломолей азота, находившегося при температуре 20 °С, до давления 2 атм. термостату отдано 20 кДж теплоты. Определить давление, под которым находился азот до сжатия, и работу, совершенную над газом при сжатии.
4. Водород при нормальных условиях имел объем V₁ = 100 м³. Найти изменение внутренней энергии газа при его адиабатическом расширении до объема V₂ = 150 м³.
5. В цилиндре под поршнем находится водород масcой m = 0,02 кг при температуре Т₁ = 300 К. Водород сначала расширился адиабатически, увеличив свой объем в пять раз, а затем был сжат изотермически, причем объем газа уменьшился в пять раз. Найти температуру Т₂ в конце адиабатного расширения и полную работу, совершенную газом. Изобразить процесс графически.
6. Кислород массой 2 кг занимает объем 1 м³ и находится под давлением 0,2 МПа. При нагревании газ расширился при постоянном давлении до объема 3 м³ , а затем давление его возросло до 0,5 МПа при неизменном объеме. Найти изменение внутренней энергии газа, совершенную им работу и переданное газу количество теплоты.
7. Какова удельная теплоемкость с_v смеси газов, содержащей кислород m₁ = 10 г и азот m₂ = 20 г?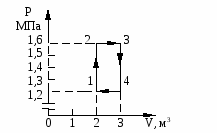




8. Идеальный двухатомный газ, содержащий количество вещества  = 1 кмоль, совершает замкнутый цикл, график которого изображён на рисунке. Определить 1) количество теплоты полученное, от нагревателя; 2) количество теплоты, переданное охладителю; 3) работу, совершаемую газом за цикл; 4) к.п.д цикла .




9. Идеальный двухатомный газ совершает цикл Карно, график которого изображен на рисунке. Объемы газа в состояниях В и C соответственно V₁ = 12 л и V₂ = 16 л. Найти к.п.д цикла .
10. Вычислить приращение энтропии ∆S при нагревании 1 кмоль трехатомного газа от 0 °С до 500 °С, если процесс нагревания происходит: а) при постоянном объеме; б) при постоянном давлении.
11. 2 кг льда, находящегося при t = ^18°С, нагрели и превратили в пар. Определить изменение энтропии в этом процессе. Температура плавления 273 К, температура парообразования 373 К (удельная теплоемкость льда с_л = 2,1·10³ Дж/(кгК), удельная теплоемкость воды с_в = 4,2·10³ Дж/(кгК), удельная теплота плавления льда  = 3,3·10⁵ Дж/(кгК), удельная теплота парообразования r = 23·10⁵ Дж/кг).
Задачи для самостоятельного решения
1. При адиабатном расширении кислорода с начальной температурой T₁ = 320 K внутренняя энергия уменьшилась на ∆U = 8,4 кДж, а его объем увеличился в n = 10 раз. Определить массу m кислорода.

2. Баллон вместимостью V = 20 л содержит водород при температуре T = 300 К под давлением р = 0,4 МПа. Каковы будут температура T₁ и давление р₁, если газу сообщить количество теплоты Q = 6 кДж?

3. Водород занимает объем 10 м³ при давлении 10⁵ Па. Газ нагрели при постоянном объеме до давления 3·10⁵ Па. Определить изменение внутренней энергии газа, работу, совершенную газом, и количество теплоты, сообщенное газу.

4. Азот нагревался при постоянном давлении, причем ему соoбщено количество теплоты Q = 21 кДж. Определить работу A, которую совершил при этом газ, и изменение его внутренней энергии∆U.

5. Кислород при неизменном давлении р = 80 кПа нагревается. Его объем увеличивается от V₁ = 1 м³ до V₂ = 3 м³. Определить: 1) изменение внутренней энергии кислорода; 2) работу, совершенную им при расширении; 3) количество теплоты, сообщенное газу.

6. Для нагревания углекислого газа на 50 °С при постоянном давлении требуется 3,3·10⁵ Дж тепла. Определить массу углекислого газа, работу расширения и изменение внутренней энергии.

7. Азот массой m = 200 г расширяется изотермически при температуре Т = 280 К, причем объем газа увеличивается в два раза. Найти: 1) изменение внутренней энергии газа; 2) совершенную при расширении газа работу; 3) количество теплоты, полученное газом.

8. Азот, занимавший объем V₁ = 10 л под давлением р₁ = 0,2 МПа, изотермиче­ски расширился до объема V₂ = 28 л. Определить работу расширения газа и количе­ство теплоты, полученное газом.

9. При изотермическом расширении кислорода, содержавшего количество вещества  = 1 моль и имевшего температуру Т = 300 К, газу было передано количество теплоты Q = 2 кДж. Во сколько раз увеличился объем газа?

10. При адиабатном сжатии кислорода массой m = 20 г его внутренняя энергия увеличилась на ∆U = 8 кДж и температура повысилась до Т₂ = 900 К. Найти: 1) повышение температуры ∆Т; 2) конечное давление газа Р₂, если начальное давление Р₁ = 200 кПа.

11. Кислород массой 10 г, находящийся при температуре 370 К, подвергли адиабатическому расширению, в результате которого его давление уменьшилось в 4 раза. В результате последующего изотермического процесса газ сжимается до первоначального давления. Определить: 1) температуру газа в конце процесса; 2) количество теплоты, отданное газом; 3) приращение внутренней энергии газа; 4) работу, совершенную газом.

12. Некоторая масса газа, занимающего объем V₁ = 0,01 м³, находится при давлении Р₁ = 0,1 МПа и температуре Т₁ = 300 К. Газ нагревается вначале при постоянном объеме до температуры Т₂ = 320 К, а затем при постоянном давлении до температуры Т₃ =350 К. Найти работу, совершаемую газом при переходе из начального состояния в конечное.

13. Кислород массой 5 кг занимает объем 1,5 м³ и находится под давлением 3 атм. Газ нагрет сначала при постоянном давлении до объема 4 м³, а затем при постоянном объеме до давления 5 атм. Найти изменение внутренней энергии газа и совершенную им работу.

14. Водород массой 40 г, имевший температуру 300 К, адиабатно расширился, увеличив объем в 3 раза. Затем при изотермическом сжатии объем газа уменьшился в 2 раза. Определить полную работу, совершенную газом, и конечную температуру газа.

15. Кислород массой 200 г занимает объем 100 л и находится под давлением 200 кПа. При нагревании газ расширился при постоянном давлении до объема 300 л, а затем его давление возросло до 500 кПа при неизменном объеме. Найти изменение внутренней энергии газа, совершенную им работу и теплоту, переданную газу.

16. Моль идеального газа имеет первоначально температуру 290 К. Газ расширяется изобарически до тех пор, пока его объем не возрастет в два раза. Затем газ охлаждается изохорически до первоначальной температуры. Определить приращение внутренней энергии газа, работу, совершенную газом, и количество теплоты, полученное газом.

17. В цилиндре под поршнем находится водород массой 0,02 кг при температуре 300 К. Водород сначала расширился адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце адиабатического расширения и полную работу, совершенную газом. Изобразить процесс графически на диаграмме "давление - температура".

18. Некоторая масса кислорода занимает объем V₁=3 л при температуре t₁ = 27°С и давлении p₁ = 8,2·10⁵ Па. Во втором состоянии газ имеет параметры V₂=4,5 л и p₂=6·10⁵ Па. Найти: количество тепла, полученного газом; работу, совершенную газом при расширении; изменение внутренней энергии газа. Задачу решить при условии, что перевод газа из первого состояния во второе осуществляется: 1) путем АСВ и 2) путем АDВ.

19. Азот массой m = 50 г находится при температуре T₁ = 280 K. В результате изохорного охлаждения его давление уменьшилось в 2 раза, а затем в результате изобарного расширения температура газа в конечном состоянии стала равной пер­воначальной. Определите: 1) работу, совершенную газом; 2) изменение внутренней энергии газа.

20. Двухатомный идеальный газ занимает объем V₁ = 1 л и находится под давлением p₁ = 0,1 МПа. После адиабатического сжатия газ характеризуется объемом V₂ и давлением p₂. В результате последующего изохорного процесса газ охлаждается до первоначальной температуры, а его давление p₃ = 0,2 МПа. Определить: 1) объем V₂; 2) давление p₂.

21. Считая азот идеальным газом, определить его удельную теплоемкость: 1) для изохорного процесса; 2) для изобарного процесса.

22. Определить удельные теплоемкости c_v и c_p смеси углекислого газа массой m₁ = 3 г и азота массой m₂ = 4 г.

23. Определить удельную теплоемкость с_p смеси кислорода и азота, если количество вещества первого компонента равно 2 моль, а количество вещества второго  4 моль.

24. Смесь газов состоит из хлора и криптона, взятых при одинаковых условиях и в равных объемах. Определить удельную теплоемкость с_p смеси.

25. Вычислить удельные теплоемкости c_v и с_p газов: 1) гелия; 2) водорода; 3) углекислого газа.

26. Разность удельных теплоемкостей (c_р - с_v) некоторого двухатомного газа равна 260 Дж/(мольК). Найти молярную массу  газа и его удельные теплоемкости с_v и с_р.

27. Дана смесь газов, состоящая из неона, масса которого m₁= 4 кг и водорода, масса которого m₂ = 1 кг. Газы считать идеальными. Определить удельные теплоемкости смеси газов в процессах: р = соnst, V = соnst.

28. Принимая отношение теплоемкостей для двухатомных газов n = 1,4, вычислить удельные теплоемкости кислорода.

29. Найти отношение с_p/с_v для смеси газов, состоящей из 10 г гелия и 4 г водорода.

30. Вычислить отношение c_р/с_v для смеси 3 моль аргона и 5 моль кислорода.

31. Идеальный многоатомный газ совершает цикл, состоящий из двух изохор и двух изобар, причем наибольшее давление газа в два раза больше наименьшего, а наибольший объем в четыре раза больше наименьшего. Определить к. п. д. цикла .

32. Идеальный газ, совершающий цикл Карно, 2/3 количества теплоты Q₁, полученного от нагревателя, отдает охладителю. Температура Т₂ охладителя равна 280 К. Определить температуру Т₁ нагревателя.

33. Идеальный газ совершает цикл Карно. Температура Т₂ охладителя равна 290 К. Во сколько раз увеличится к. п. д. цикла, если температура нагревателя по­высится от 400 К до 600 К?

34. Идеальный газ совершает цикл Карно. Температура Т₁ нагревателя в три раза выше температуры T₂ охладителя. Нагреватель передал газу количество теплоты Q₁ = 42 кДж. Какую работу А совершил газ?

35. Газ совершил цикл Карно. Абсолютная температура нагревателя в три раза выше, чем температура холодильника. Нагреватель передал газу количество теплоты 5 кДж. Какую работу совершил газ?

36. Газ совершает цикл Карно. За счет теплоты 4200 Дж, полученной от нагревателя, он совершает работу 598 Дж. Каков к. п. д. цикла? Во сколько раз абсолютная температура нагревателя больше абсолютной температуры холодильника?

37. Газ совершает цикл Карно. Работа изотермического расширения газа 5 Дж. Определить работу изотермического сжатия, если КПД цикла равен 0,2.

38. Идеальный газ совершает цикл Карно, Температура нагревателя 220 °С, температура холодильника 7 °С. При изотермическом расширении газ совершает работу 120 Дж. Определить количество теплоты, которое газ отдает холодильнику при изотермическом сжатии.

39. В результате кругового процесса газ совершил работу 5 Дж и отдал холодильнику 16,8 Дж теплоты. Определить к. п. д. цикла.

40. Совершая замкнутый процесс, газ получил от нагревателя количество теплоты Q₁ = 4 кДж. Определить работу А газа при протекании цикла, если его к. п. д.  = 0,1.

41.В результат кругового процесса газ совершил работу А = 1 Дж и передал охладителю количество теплоты Q₂ = 4,2 Дж. Определить к. п. д. цикла.

42.Идеальный газ, совершающий цикл Карно, произвел работу 600 Дж. Темпе­ратура нагревателя 500 К, холодильника 300 К. Определить: 1) к. п. д. цикла; 2) количество теплоты, отданное холодильнику за один цикл.

43.Идеальный газ, совершающий цикл Карно, 70 % количества теплоты, полученной от нагревателя, отдает холодильнику. Количество теплоты, получаемое от нагревателя, равно 5 кДж. Определить: 1) к. п. д. цикла; 2) работу, совершенную при полном цикле.

44. Наименьший объем газа, совершающего цикл Карно, равен 153 л. Определить наибольший объем, если объем газа в конце изотермического расширения составляет 189 л, а в конце изотермического сжатия  160 л.

45. Определить к. п. д. цикла, состоящего из двух адиабат и двух изохор, совер­шаемого идеальным газом, если известно, что в процессе адиабатного расширения абсолютная температура газа Т₂ = 0,75·Т₁, а в процессе адиабатного сжатия Т₄ = 0,75·Т₃.

46. Идеальная тепловая машина, работающая по циклу Карно, имеет температуру нагревателя 227 °С, температуру холодильника 127 °С. Во сколько раз нужно увеличить температуру нагревателя, чтобы к. п. д. машины увеличился в 3 раза?

47. Идеальная тепловая машина, работающая по циклу Карно, получает за каждый цикл от нагревателя 2514 Дж. Температура нагревателя 400 К, холодильника - 300 К. Найти работу, совершаемую машиной за один цикл, и количество тепла, отдаваемое холодильнику за один цикл.

48. Идеальная тепловая машина работает по циклу Карно. При этом 80 % тепла, получаемого от нагревателя, передается холодильнику. Количество тепла, получае­мого от нагревателя, равно 6,3 кДж. Найти: 1) к. п. д. цикла; 2) работу, совершен­ную при полном цикле.

49. Один киломоль кислорода совершает цикл Карно в интервале температур от 27 °С до З27 °С. Известно, что отношение максимального за цикл давления к мини­мальному равно 20. Вычислить: 1) к. п. д. цикла; 2) количество теплоты, получен­ное от нагревателя за цикл ; 3) количество теплоты, отданное холодильнику за цикл; 4) работу, совершаемую газом за цикл.

50. Идеальный газ совершает цикл Карно. Температура Т₁ нагревателя равна 470 К, температура Т₂ охладителя равна 280 К. При изотермическом расширении газ совершает работу А = 100 Дж. Определить к. п. д. цикла , а также количество теплоты Q₂, которое газ отдает охладителю при изотермическом сжатии.

51. Идеальный газ совершает цикл Карно. Температура T₁ нагревателя в четыре раза выше температуры T₂ охладителя. Какую долю количества теплоты, получаемого за один цикл от нагревателя, газ отдает охладителю?

52. Идеальная тепловая машина. работающая по циклу Карно, совершает за одни цикл работу 7,35·10⁴ Дж. Температура нагревателя 100 °С, температура холодильника 0° С, Найти: I) к. п. д. машины; 2) количество тепла, получаемого машиной за один цикл от нагревателя; 3) количество тепла, отдаваемого за один цикл холодильнику.

53. Многоатомный идеальный газ совершает цикл Карно, при этом в процессе адиабатического расширения объем газа увеличивается в 4 раза. Определить к. п. д. цикла.

54.Идеальный двухатомный газ, содержащий количество вещества  = 1 моль, совершает цикл, состоявший из двух изохор и двух изобар Наименьший объем V_min = 10 л, наибольший V_max= 20 л, наименьшее давление p_min = 246 кПа, наибольшее p_max=410 кПа. Построить график цикла. Определить к. п. д.

55. Идеальный газ совершает цикл Карно, к. п. д. которого 0,4. Определить работу изотермического сжатия газа, если работа изотермического расширения 400 Дж.

56. Газ совершает цикл Карно. Температура холодильника 280 К, нагревателя 380 К. Во сколько раз увеличится коэффициент полезного действия цикла, если температуру нагревателя повысить на 200 К?

57.Опеределить к. п. д. цикла изображенного на рисунке. Рабочим телом является идеальный одноатомный газ, p₂ = 2p₁, V₂ = 4V₁.
5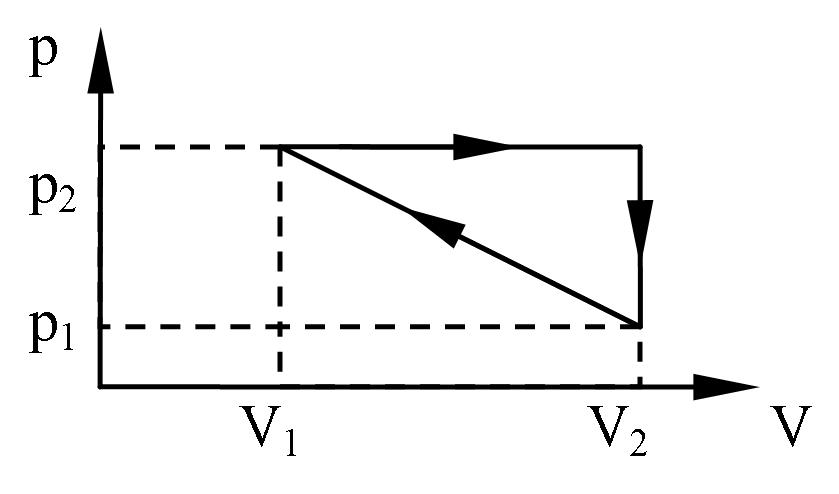8. Тепловая машина, рабочим телом которой является идеальный двухатомный газ, совершает цикл, изображенный на рисунке. Найти к. п. д. этой машины, если p₂ = 2p₁, V₂ = 4V₁.

59. Идеальная тепловая машина работает по циклу Карно. Определить КПД цикла, если известно, что за один цикл была произведена работа, равная 3000 Дж, и холодильнику было передано 13,4 кДж тепла.

60. В результата циклического процесса газ совершил работу А = 100 Дж и передал холодильнику 400 Дж теплоты. Определить коэффициент полезного действия цикла.

61. Смешали воду массой m₁ = 5 кг при температуре T₁ = 280 K с водой массой m₂ = 8 кг при температуре T₂ = 350 K. Найти: 1) температуру смеси; 2) изменение энтропии ∆S, происходящее при смешивании.

62. В результате изохорного нагревания водорода массой m = 1 г давление p газа увеличилось в два раза. Определить изменение ∆S энтропии газа.

63. Найти изменение ∆S энтропии при изобарном расширении азота массой m = 4 г от объема V₁ = 5 л до объема V₂ = 9 л.

64. Кусок льда массой m = 200 г, взятый при температуре t_{1 =} -10 °С, был нагрет до температуры t₂ = 0 °С и расплавлен, после чего образовавшаяся вода была нагрета до температуры t₁= 10 °С. Определить изменение энтропии ∆S в ходе указанных процессов.

65. Лед массой m₁ = 2 кг при температуре t₁ = 0 °С был превращен в воду той же температуры с помощью пара, имеющего температуру T₂ = 100 °С. Определить массу m₂ израсходованного пара. Каково изменение энтропии ∆S системы лед - пар?

66. Кислород массой m = 2 кг увеличил свой объем в 5 раз один раз изотермически, другой - адиабатно. Найти изменение энтропии в каждом из указанных процессов.

67. Вычислить изменение энтропии двух молей идеального двухатомного газа, если его температура изохорически повышается от 200 К до 300 К. Убывает энтропия газа или возрастает?

68. Вычислить изменение энтропии при изотермическом сжатии трех молей идеального газа от 20 до 15 л. Убывает энтропия газа или возрастает ? Газ двухатомный.

69. Вычислить изменение энтропии при изотермическом изменении давления шести молей идеального одноатомного газа от 9 до 6 МПа при комнатной температуре. Уменьшается или увеличивается при этом энтропия газа?

70. Вычислить изменение энтропии при изотермическом изменении давления трех молей идеального двухатомного газа от 5 до 7 МПа при комнатной температуре.

71. Вычислить изменение энтропии при изобарическом нагревании пяти молей идеального одноатомного газа от 200 до 300 К. Увеличивается или уменьшается при этом энтропия газа?

72. Вычислить изменение энтропии двух молей идеального двухатомного газа, если его давление изохорически увеличивается от 2 до 3 МПа. Увеличивается или уменьшается энтропия газа в этом случае?

73. Вычислить изменение энтропии восьми молей идеального одноатомного газа, если его температура изохорически убывает от 325 до 285 К. Убывает или возрастает энтропия газа ?

74. Вычислить изменение энтропии трех молей идеального одноатомного газа, если ему изобарически сообщается 5 кДж тепла. Первоначальная температура газа равна 300 К. Увеличивается или уменьшается энтропия газа в этом случае ?

75. Вычислить изменение энтропии семи молей идеального одноатомного газа, если его давление изохорически уменьшается от 7 до 5 МПа. Увеличивается или уменьшается энтропия газа?

76. Вычислить изменение энтропии пяти молей идеального одноатомного газа, если у него изохорически отнимается 3 кДж тепла. Начальная температура газа равна 350 К. Увеличивается или уменьшается энтропия газа?

77. 1 кмоль двухатомного идеального газа находится при некоторой температуре, охлаждается изохорически, вследствие чего его давление уменьшается в два раза. Затем газ изобарически расширяется так, что в конечном состоянии его температура равна первоначальной. Найти приращение энтропии.

78. Водород массой m = 100 г был изобарно нагрет так, что его объем, увеличился в 3 раза, затем водород был изохорно охлажден так, что давление его уменьшилось в 3 раза. Найти изменение ∆S энтропии в ходе указанных процессов.

79. Вычислить изменение энтропии двух молей идеального двухатомного газа, если ему изохорически сообщаются 5 Дж тепла. Начальная температура газа равна 250 К.

80. Вычислить изменение энтропии четырех молей идеального одноатомного газа, если он изотермически отдает количество тепла 7 кДж. Температур газа равна 350 К. Увеличивается или уменьшается энтропия газа?

81. Вычислить изменение энтропии трех молей идеального двухатомного газа, если ему изотермически сообщается количество тепла 4 кДж. Температура газа равна 300 К.

82. Вычислить изменение энтропии пяти молей идеального двухатомного газа, если от него изобарически забирают 3 кДж тепла. Начальная температура газа равна 330 К.

83. Найти приращение энтропии при превращении 200 г льда, находившегося при температуре минус 10,7 °С, в воду. Теплоемкость льда считать не зависящей от температуры. Температуру плавления принять равной 273 К.

84. Вычислить изменение энтропии трех молей идеального двухатомного газа, если газ изобарически сжимают от 2 до 1 л при комнатных температурах. Увеличивается или уменьшается при этом энтропия газа?

85. Найти изменение энтропии при переходе 8 г кислорода от объема в 10 л при температуре 80 °С к объему в 40 л при температуре 300 °С.

86. 6,6 г водорода расширяется изобарически изобарически до увеличения объема в два раза. Найти изменение энтропии при этом расширении.

87. Найти изменение энтропии ∆S 5 г водорода, изотермически расширившегося от объема 10 л до объема 25 л.

88. Найти приращение энтропии ∆S при расширении 2 г водорода от объема 1,5 л до объема 4,5 л, если процесс расширения происходит при постоянном давлении.

89. 10 г кислорода нагревают от t₁ = 50 °С до t₂ = 150 °С. Найти изменение энтропии, если нагревание происходит: 1) изохорически; 2) изобарически.

90. При нагревании 1 кмоль двухатомного газа его абсолютная температура увеличивается в 1,5 раза. Найти изменение энтропии, если нагревание происходит 1) изохорически; 2) изобарически.