Контрольная. 120101 МР для ЗО МДК 01.02 Калачева Н.А. нов-1. Методические указания по выполнению контрольной работы для студентов заочной формы обучения, осваивающих профессиональный модуль пм. 01 Выполнение работ по созданию геодезических, нивелирных сетей и сетей специального назначения
 Скачать 0.89 Mb.
|
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯРОСТОВСКОЙ ОБЛАСТИГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОСТОВСКОЙ ОБЛАСТИ «РОСТОВСКИЙ-НА-ДОНУ АВТОДОРОЖНЫЙ КОЛЛЕДЖ»  МДК 01.02 МЕТОДЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ПОЛЕВЫХ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ И ОЦЕНКА ИХ ТОЧНОСТИ Методические указания по выполнению контрольной работы для студентов заочной формы обучения, осваивающих профессиональный модуль ПМ. 01 « Выполнение работ по созданию геодезических, нивелирных сетей и сетей специального назначения» в рамках основной профессиональной образовательной программы по специальности 120101 Прикладная геодезия на основе ФГОС СПО Ростов-на-Дону 2012
МДК 01.02 «Методы математической обработки результатов полевых геодезических измерений и оценка их точности»: Методические указания по выполнению контрольной работы для студентов заочной формы обучения, осваивающих профессиональный модуль ПМ. 01 «Выполнение работ по созданию геодезических, нивелирных сетей и сетей специального назначения» в рамках основной профессиональной образовательной программы по специальности 120101 Прикладная геодезия на основе ФГОС СПО Методические указания включают тематический план и содержание рабочей программы профессионального модуля, отнесенных к МДК 01.01 «Геодезические измерения для определения координат и высот пунктов геодезических сетей и сетей специального назначения», содержат общие сведения о порядке, правилах подготовки и представления домашней письменной контрольной работы, варианты контрольных заданий, разъяснения по производимым расчетам, рекомендуемые информационно-библиографические ресурсы. Предназначаются студентам заочной формы обучения. Рассмотрено на заседании цикловой комиссии профессионального цикла специальности 120101 Прикладная геодезия (протокол № 2 от 9 октября 2012).
© Методический отдел РАДК, 2012 СОДЕРЖАНИЕ
ВВЕДЕНИЕ В МДК 01.02 «Методы математической обработки результатов полевых геодезических измерений и оценка их точности» рассматриваются теория ошибок измерений, способы создания геодезических сетей, обработка результатов измерений в этих сетях. Решением этих задач занимается дисциплина ТМОГИ «Теория математической обработки геодезических измерений». ТМОГИ включает в себя «Теорию ошибок измерений», которая изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок - нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений. По своей природе ошибки бывают грубые, систематические и случайные. Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются. Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений. Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то есть, при большом количестве измерений; такие закономерности называют статистическими. Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям: - при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой, - положительные и отрицательные случайные ошибки равно возможны, - среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений, - малые по абсолютной величине случайные ошибки встречаются чаще, чем большие. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок. При производстве геодезических измерений, кроме необходимых, достаточных для однозначного получения искомых величин, выполняются измерения избыточные. При их наличии возникает неоднозначность получения определяемых величин, что приводит к невязкам. В процессе математической обработки геодезических измерений необходимо исправить их результаты так, чтобы удовлетворить все математические связи, т. е. устранить невязки. Процесс математической обработки, направленный на устранение невязок, называется уравниванием. Вторая задача математической обработки - оценка точности измеренных и уравненных величин. Уравнивание под условием [pν²] = min называют уравниванием по методу наименьших квадратов (МНК). Это задача на условный экстремум имеет два основных способа решения - коррелатный и параметрический. Первый - способ Лагранжа с неопределенными множителями для нахождения условного экстремума. Второй - способ абсолютного минимума, когда все измеренные величины представляют в виде функций некоторых параметров. Существуют также комбинированные способы - коррелатный с дополнительными неизвестными и параметрический, с избыточными параметрами ФГОС СПО устанавливает следующие требования к результатам освоения профессионального модуля ПМ.01 «Выполнение работ по созданию геодезических, нивелирных сетей и сетей специального назначения», в том числе к умениям и знаниям подготовки выпускников, завершивших изучение МДК 01.02 «Методы математической обработки результатов полевых геодезических измерений и оценка их точности». Выпускник в ходе освоения профессионального модуля должен: иметь практический опыт: полевых работ по созданию, развитию и реконструкции геодезических сетей; поверки и юстировки геодезических приборов и систем; по полевому обследованию пунктов геодезических сетей; уметь: выполнять полевые геодезические измерения в геодезических сетях; обследовать пункты геодезических сетей; исследовать, поверять и юстировать геодезические приборы; осуществлять первичную математическую обработку результатов полевых измерений; знать: нормативные требования создания геодезических сетей; устройство и принципы работы геодезических приборов и систем; методы угловых и линейных измерений, нивелирования и координатных определений; особенности поверки и юстировки геодезических приборов и систем; техники выполнения полевых и камеральных геодезических работ по созданию, развитию и реконструкции отдельных элементов государственных геодезических, нивелирных сетей и сетей специального назначения; основы современных технологий определения местоположения пунктов геодезических сетей на основе спутниковой навигации; методы электронных измерений элементов геодезических сетей; алгоритмы математической обработки результатов полевых геодезических измерений с использованием современных компьютерных программ; основы анализа и приемы устранения причин возникновения брака и грубых ошибок измерений; приемы контроля результатов полевых и камеральных геодезических работ В МДК 01.02 рассмотрен раздел ТМОГИ по уравниванию государственных геодезических сетей, плановых и высотных. 1 ТЕМАТИЧЕСКИЙ ПЛАН И СОДЕРЖАНИЕ МДК 01.02 «Методы математической обработки результатов полевых геодезических измерений и оценка их точности»1
2 ОПРЕДЕЛЕНИЕ ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ Контрольная работа выполняется по одному из вариантов, номер которого для каждого студента определяется по двум последним цифрам его личного шифра и количеству букв в его фамилии. Если две последние цифры (N) его шифра от 1 до 30, то для определения варианта применяется следующая формула: № = N+K, где K – количество букв в его фамилии. Если две последние цифры (N) его шифра от 31 до 60, то для определения варианта применяется следующая формула: № = (N-30)+K, где K – количество букв в его фамилии. Если две последние цифры (N) его шифра от 61 до 90, то для определения варианта применяется следующая формула: № = (N-60)+K, где K – количество букв в его фамилии. Если две последние цифры (N) его шифра от 91 до 100, то для определения варианта применяется следующая формула: № = (N-90)+K, где K – количество букв в его фамилии. Например, личный шифр студента Иванова И.И. обозначен цифрами 7499, тогда вариант контрольного задания определяется следующим образом: устанавливаются две последние цифры – это 99, затем находится число для вычитания – это 90, количество букв в его фамилии «Иванов» - 6 ; далее производится простое арифметическое действие (99–90)+6 = 15 и устанавливается номер варианта; в данном примере - это вариант № 15. Самостоятельная замена или произвольный выбор студентом варианта контрольного задания не допускается. 3 МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ 3.1 Введение Обязательным видом самостоятельной работы студентов заочной формы обучения, изучающих МДК 01.02 «Методы математической обработки результатов полевых геодезических измерений и оценка их точности», является домашняя письменная контрольная работа, которая одновременно выполняет функции средства приобретения и углубления знаний, а также их контроля и оценки. Контрольная работа является неотъемлемой частью учебной программы, выполняется студентом в межсессионный период и представляется к рецензированию в сроки, установленные графиком учебного процесса. Выполнение контрольной работы демонстрирует способность студентов применить умения и знания при уравнивании полигонометрического хода двухгрупповым способом по МНК. Завершенная контрольная работа представляет собой выполненные расчеты по уравниванию разомкнутого полигонометрического хода, оформленные в виде таблиц. Контрольная работа по МДК 01.02 выполняется после предварительного ознакомления с требованиями ФГОС СПО к результатам освоения профессионального модуля ПМ.01«Выполнение работ по созданию геодезических, нивелирных сетей и сетей специального назначения», рабочей программой по данному модулю, изучения рекомендованных информационно-библиографических ресурсов. Выполнение контрольной работы состоит из следующих этапов: 1) ознакомление с содержанием МДК 01.02 «Методы математической обработки результатов полевых геодезических измерений и оценка их точности»; 2) определение варианта заданий контрольной работы; 3) подбор и изучение информационно-библиографических ресурсов (учебников и учебных пособий, различных инструкций, Интернет-материалов и др.); 4) систематизация материала; 5) изучение порядка выполнения каждого задания контрольной работы; 6) консультация у преподавателя, преподающего дисциплину; 7) вычисления, их проверка, окончательное оформление работы; 8) представление выполненной работы методисту заочного отделения; 9) оценка и рецензия представленной контрольной работы преподавателем; 10) устранение автором работы указанных в рецензии замечаний; 11) подготовка к устному собеседованию по содержанию каждого задания контрольной работы. Написанию контрольной работы должен предшествовать активный поиск информационно-библиографических ресурсов по избранной теме. 3.2 Указания по выполнению контрольной работы Способы уравнивания полигонометрических ходов Полигонометрией называют метод определения положения геодезических пунктов путем построения на местности полигонометрического хода (ломанной линии) или систем ходов (полигонометрическая сеть), в которых измеряются все углы и стороны. Полигонометрические ходы опираются на исходные пункты более высокого класса. Они могут быть разомкнутыми и замкнутыми. Если ход по форме близок к прямой линии, то его называют вытянутым, в противном случае – изогнутым. Задача уравнивания возникает в том случае, когда имеются избыточные измерения. Установим, сколько избыточных измерений будет в полигонометрическом ходе, опирающемся на исходные пункты Тн и Тк и исходные направления ни к. Число избыточных измерений может быть подсчитано по формуле:  , (1)где  - число всех измерений; - число необходимых измерений (определяемых неизвестных).При проложении полигонометрического хода измеряют n сторон и n+1 углов, т.е производят всего измерений n/ =2n+1. Неизвестными, подлежащими определению в ходе, являются координаты его вершин. Всего пунктов в ходе n+1, но координаты двух из них известны, следовательно, надо определить координаты n+1-2=n-1 пунктов. Для каждого пункта необходимо найти x и y – два неизвестных. Тогда общее число неизвестных будет равно k=2(n-1). Подставим найденные значения и в формулу (1), получим: ,т.е. будет три избыточных измерения. Полигонометрические сети уравниваются двумя способами: строгим, когда уравнивание производится под условием (pvv)=min и нестрогим, раздельным, когда сначала уравниваются углы, а затем раздельно между собой приращения координат. При строгом уравнивании по методу наименьших квадратов (МНК), возникает вопрос, каким способом производить уравнивание: коррелатным или параметрическим? При уравнивании параметрическим способом число нормальных уравнений равно числу неизвестных, в данном случае 2(n-1) (всего пунктов n+1, но координаты двух из них известны, следовательно, надо определить координаты n+1-2=n-1 пунктов), т.е. чем длиннее ход, тем больше нормальных уравнений. При уравнивании коррелатным способом число нормальных уравнений определяется числом условий, а число условий – числом избыточных измерений r=n/-k =3. Следовательно, в полигонометрическом ходе независимо от числа линий и его длины будет только три нормальных уравнения. Т.о. полигонометрию целесообразно уравнивать коррелатным способом. Однако объем вычислений и в этом способе уравнивания остается значительным. Поэтому используют все возможные упрощения, вытекающие из самого способа (двухгрупповой, трехгрупповой способы уравнивания). ЗАДАНИЕ Уравнивание полигонометрического хода 4 класса двухгрупповым способом по методу наименьших квадратов (МНК) Три избыточных измерения в полигонометрическом ходе приводят, как было установлено, к возникновению трех условий и трех условных уравнений. Первое условие возникает из связи углов поворота полигонометрического хода с начальным ни конечным к дирекционными углами. Оно может быть выражено так:  , (2)где  - уравненные значения углов, равные измеренным углам  плюс поправки  :  .В зависимости от ориентации хода относительно исходных направлений в последнем слагаемом формулы (2) множитель бывает не только (n+1), но может иметь и другие значения, например, (n-2). Второе и третье условия вытекают из связи приращений координат с исходными начальными  и конечными  координатами: ,  , (3)где  ,  - уравненные значения приращений координат, равные вычисленным приращениям координат  ,  плюс поправки:  ,  .От данных трех условий перейдем к трем условным уравнениям поправок: азимутальному (угловому) и двум координатным:  ; ; (4) ,где  - невязка по измеренным углам поворота полигонометрического хода,  ,  - невязки в приращения координат, штрихи у невязок обозначают, что эти невязки получены по приращениям, вычисленным по измеренным углам (без их предварительного уравнивания). Поправки  и  - поправки к величинам зависимым, т.к. приращения координат не измерялись в поле, а вычислялись по одним м тем же углам и линиям в камеральных условиях. Поэтому условные уравнения (4) необходимо преобразовать так, чтобы вместо поправок и в них фигурировали поправки в углы  и линии  .После преобразований условные уравнения поправок (4) примут вид:  (5) .Для решения данной системы условных уравнений введем центральные координаты. Начало координат выгодно перенести в точку с координатами xц и yц (центр тяжести), которые вычисляются по формулам: 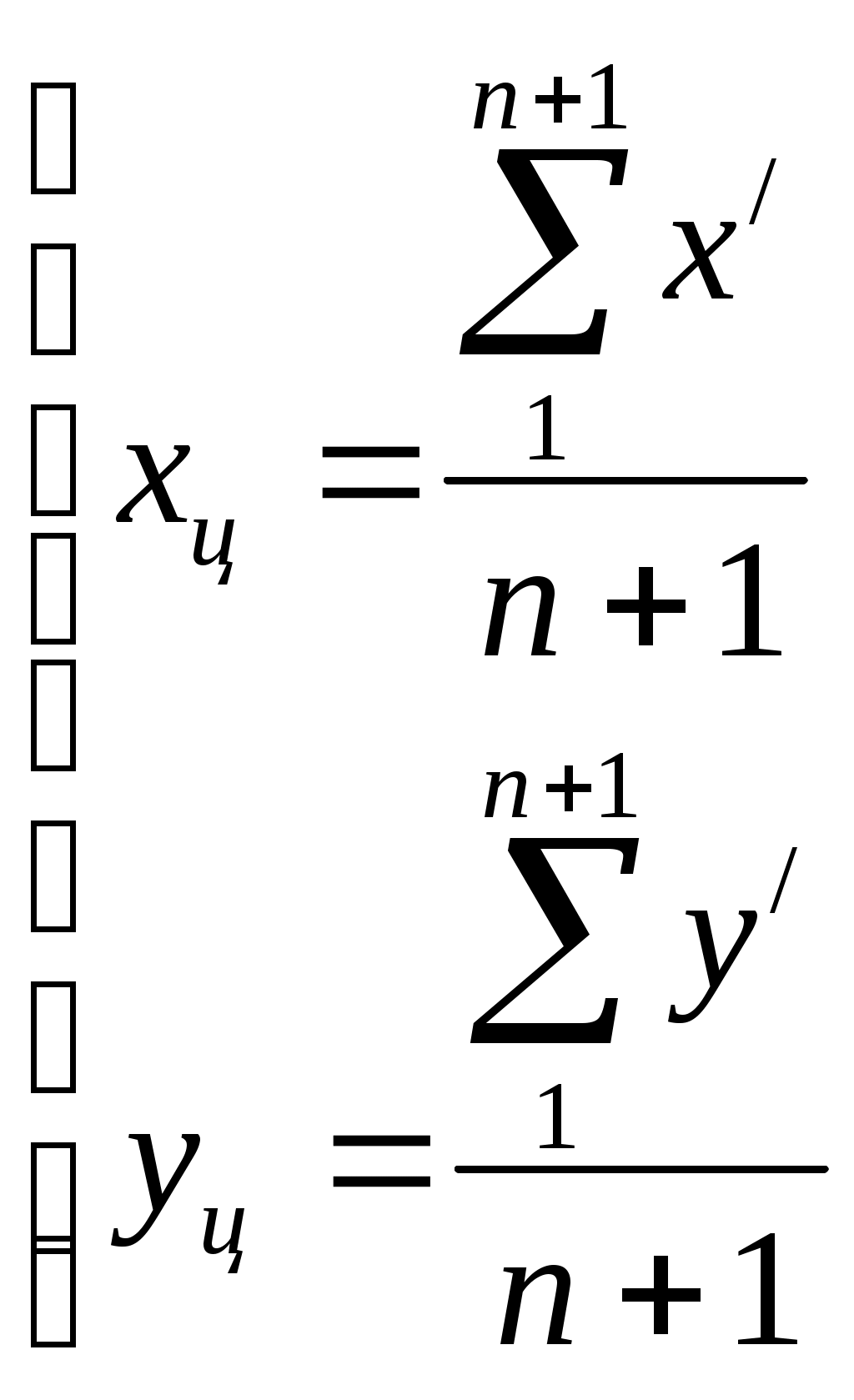 (6)где x/ и y/ - условные координаты пунктов хода. После переноса начала координат в центр тяжести новые координаты пункта называются центральными i и i. Связь центральных координат с координатами x и y, осуществляется по формулам: 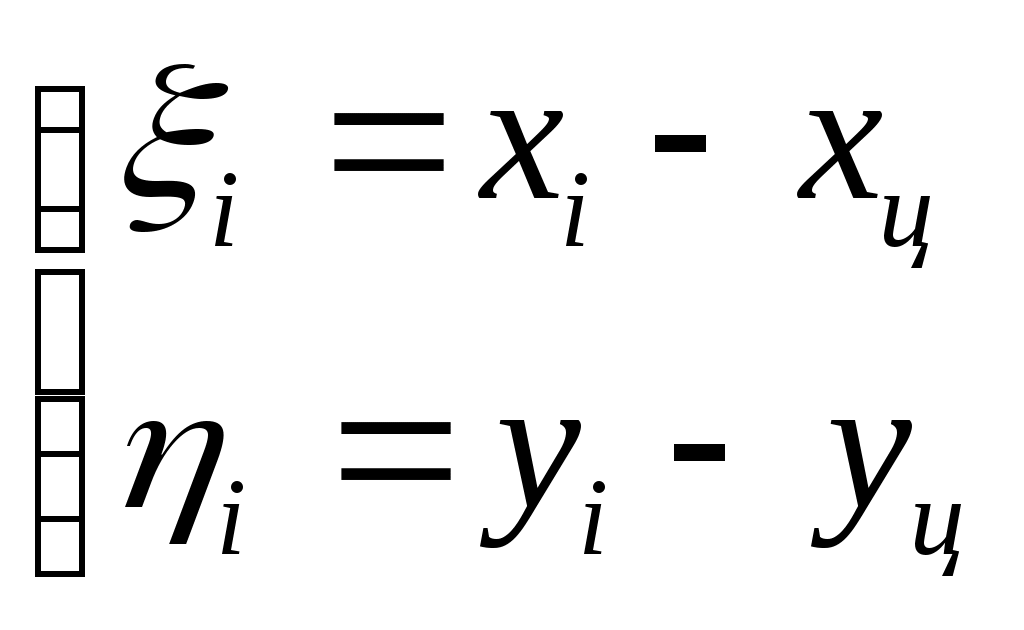 (7), а сумма центральных координат равна нулю:  (8).При параллельном переносе координат будут справедливы равенства 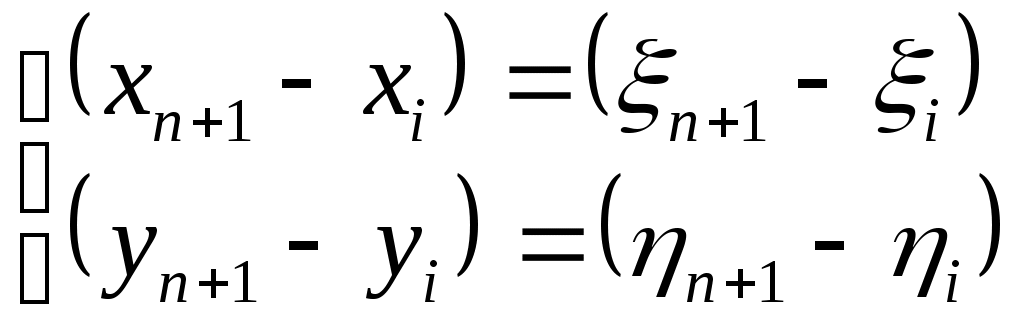 (9). Тогда условные уравнения поправок абсцисс и ординат в системе (5) можно записать относительно центральных координат:  , (10) .Условные уравнения (10) и  решим двухгрупповым способом. Разделим три условных уравнения поправок на две группы: в первую отнесем условное уравнение поправок углов, а во вторую – координат вида (10). Условное уравнение первой группы решим отдельно и найдем поправки в углы V/ - первичные поправки. Первичная поправка в угол равна невязке с обратным знаком, деленной на количество углов: . (11)Полная поправка в угол будет состоять из первичной V/ и V//вторичной поправок:  . Для нахождения вторичных поправок в углы и одновременно поправок в длины линий Vs надо совместно решить систему уравнений (10) и уравнение , но со свободными членами, вычисленными по углам, предварительно исправленными поправками V/.Т.о. уравнение можно записать в виде  , но  , тогда  . (12)Следовательно, вторичная поправка только подправляет первичную, а сумма поправок остается равной невязке f. с обратным знаком. Преобразуем коэффициенты условных уравнений второй группы, в результате чего условные уравнения (10), получат окончательный вид:  , (13)  .Системы преобразованных условных уравнений (12) и (13) будем решать под условием  . (14)Трем условным уравнениям будут соответствовать три нормальных уравнения коррелат с тремя неизвестными – коррелатами  ,  ,  . Согласно  =0. Следовательно, нормальные уравнения коррелат примут вид , (15) .Раскроем буквенные обозначения коэффициентов:  , (16) , (17) . (18)Нормальные уравнения (15) решаются способом определителей. Коррелаты 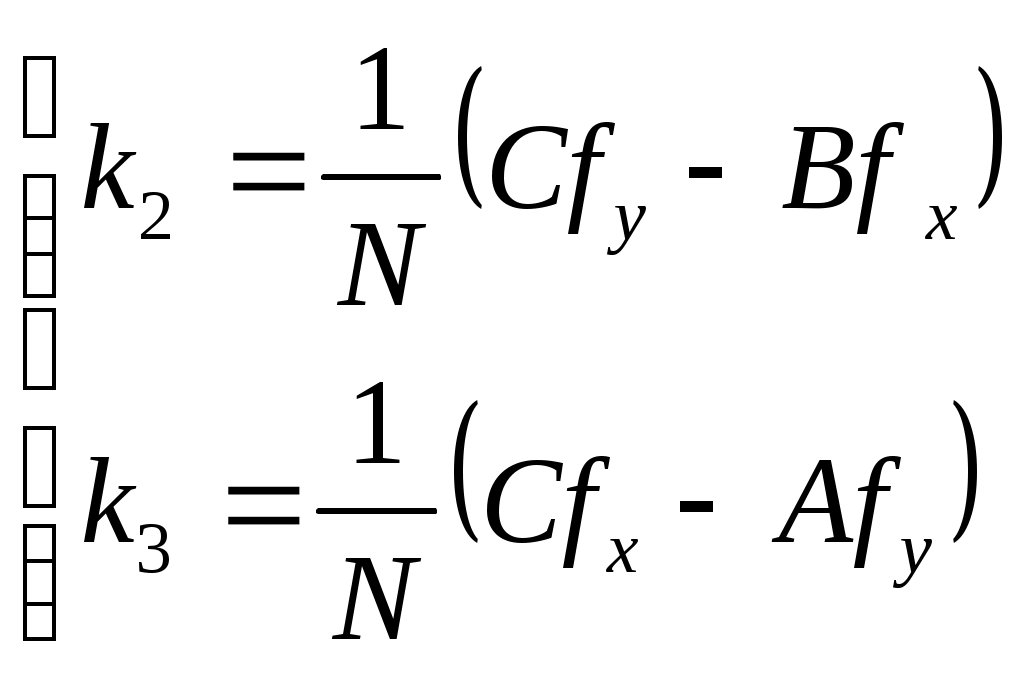и будут равны: , (19)где  . (20)Затем вычисляются вторичные поправки в углы из коррелатных уравнений V//и поправки в линии Vs: 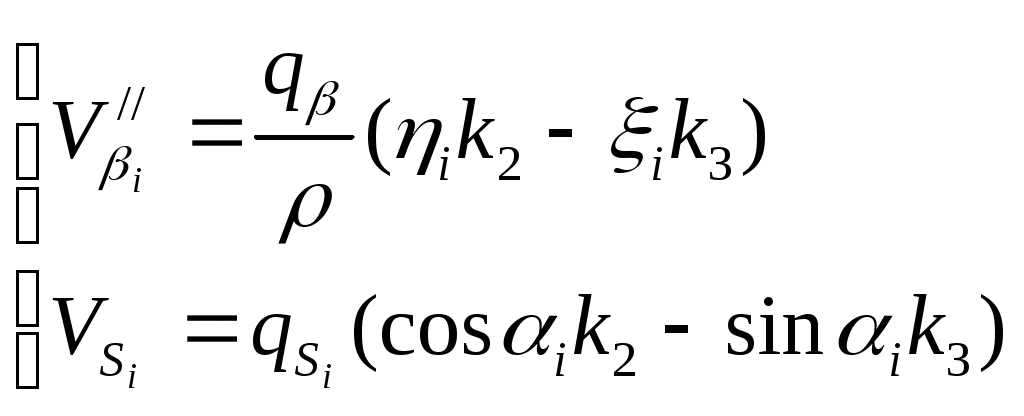 (21)Поправки в дирекционные углы находятся по формуле:  . (22)Уравненные углы, дирекционные углы и линии находятся путем введения поправок V//, Vи Vs в соответствующие значения. Поправки в приращения координат вычисляются по формулам: 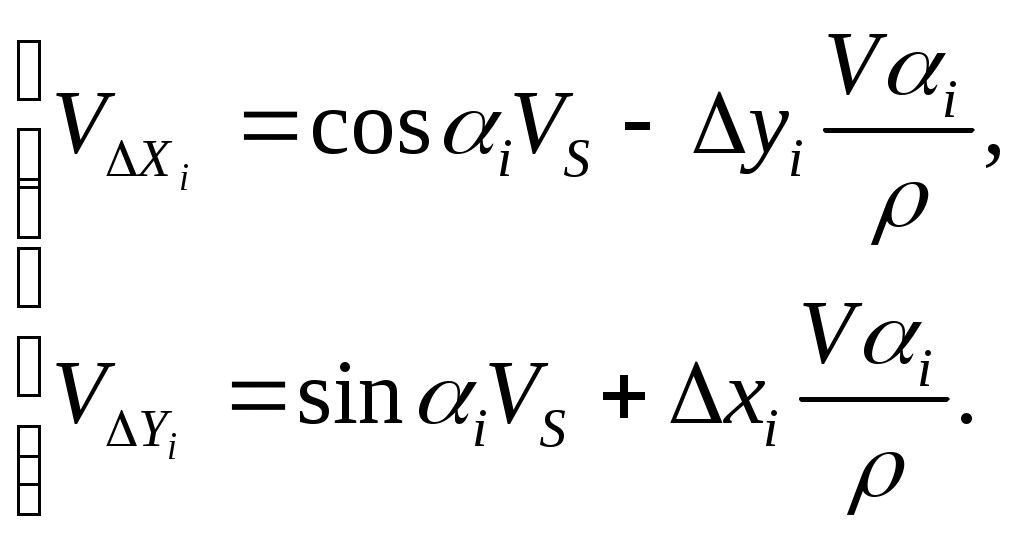 (23)Контролем вычисления поправок в приращения координат служат равенства: 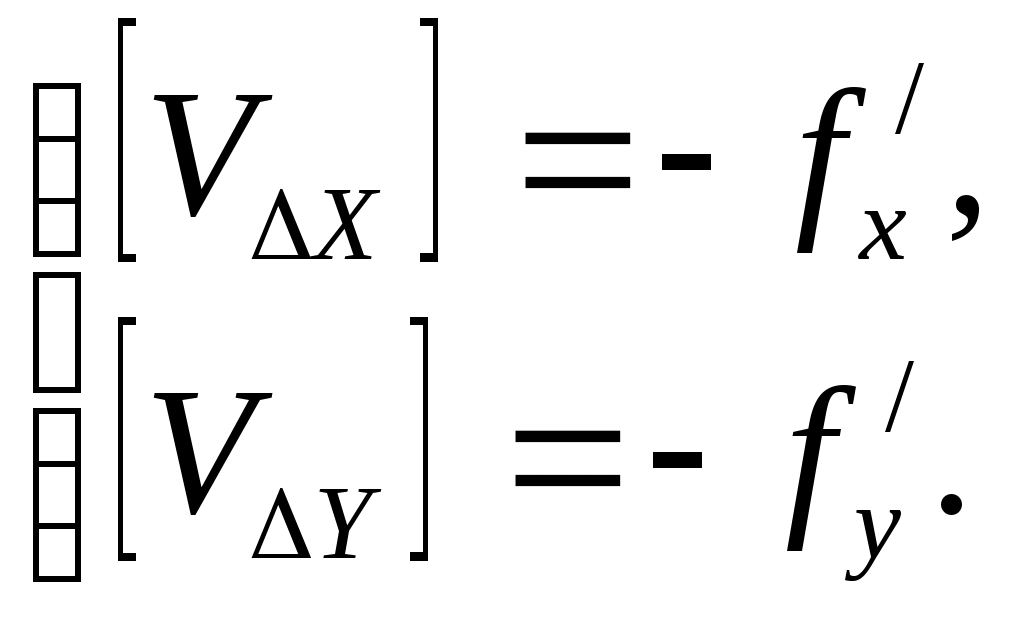 (24)По уравненным приращениям координат определяются уравненные координаты. Оценка точности в двухгрупповом способе уравнивания В формулах (21) величины  и  являются обратными весами, исходя их соотношения . (25)Вес измеренного угла и линии определяются по формулам:  или  , (26) , (27)где с – произвольная величина. При измерении линий малыми светодальномерами (топографическими) принимается 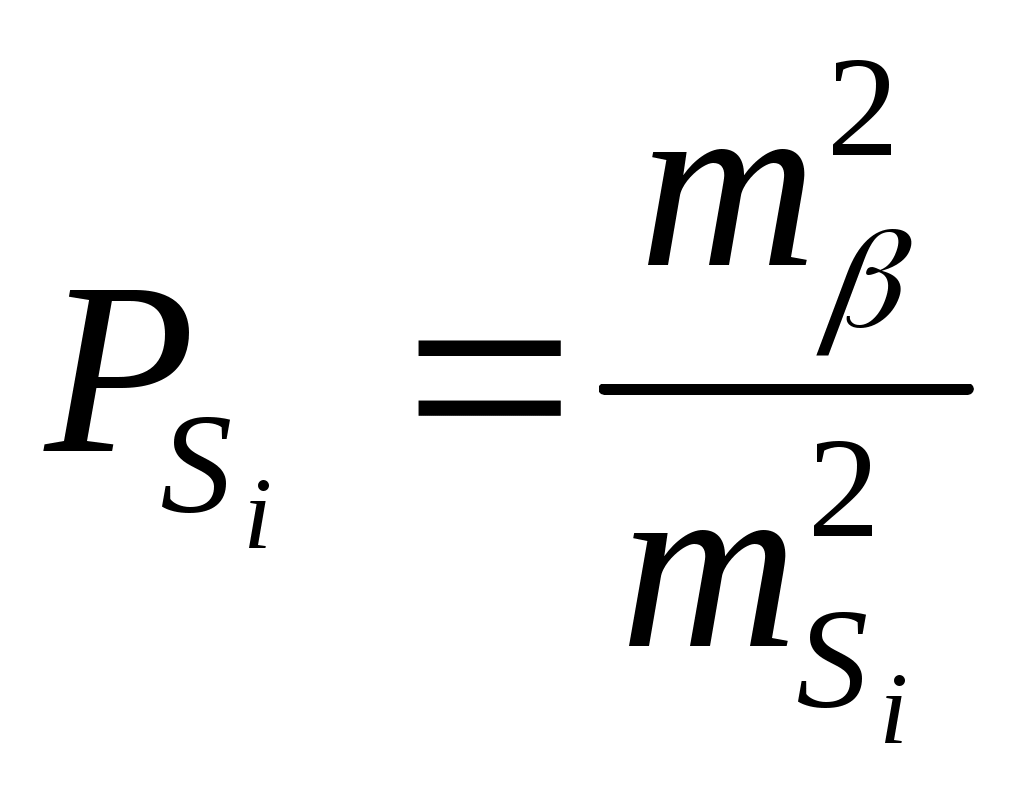 , тогда ,  . (28)При измерении линий светодальномерами типа СТ и СП веса линий можно принять практическим равными, т.е.  (29)ЗАДАНИЕ Произвести уравнивание двухгрупповым способом полигонометрического хода 4 класса. Схема хода приведена на рис.1. Найти средние квадра тические ошибки уравненных значений дирекционного угла линии (4-5) и координат пункта 5, как наиболее удаленных от исходных. 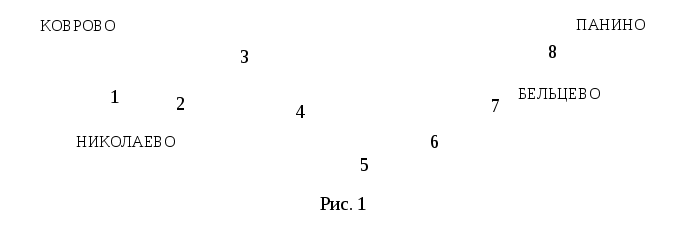 Варианты индивидуального задания выбираются из приложения 1. ПРИМЕР Исходные данные и вычисления приведены в табл.1, оценка точности в табл.2,3,4,5. ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫЧИСЛЕНИЙ Уравнивание полигонометрического хода 1. Вычисление дирекционных углов и приращений координат Определяется угловая невязка хода f  , (30)где  - сумма левых углов поворота полигонометрического хода, - начальный дирекционный угол, - конечный дирекционный угол,(n+1) – количество углов. Первичные поправки в углы вычисляются по формуле (11). По исправленным за первичную поправку углам производятся предварительные вычисления (дирекционных углов линий хода, приращений координат), в результате которых находятся невязки  ,  ,  (графы 3,6,7 табл.1). Относительная ошибка измерения линий  , для полигонометрии 4 класса, должна быть меньше  .2. Вычисление коэффициентов нормальных уравнений коррелат А,В,С В графах 10,11 табл. 1 определяются условные координаты пунктов полигонометрического хода  и  в км, принимая за начало координат первую точку хода (т.е.  ,  и т.д.). Координаты центра тяжести вычисляются по формулам (6), центральные координаты  и  - по формулам (7) и результаты заносятся в графы 12,13 табл.1. Величины , ,xц, yц, , вычисляются с округлением до 0,001 км. В графах 14-20 табл.1 (с округлением 0,001) определяются величины, входящие в формулы коэффициентов нормальных уравнений коррелат. Контролем при этом являются равенства:  , (31) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||