Методические указания по выполнению контрольной работы по дисциплине Теория принятия решений

• Название: Методические указания по выполнению контрольной работы по дисциплине Теория принятия решений
• Дата: 19.05.2022
• Размер: 314.5 Kb.
• Имя файла: Metod (1).doc
• Тип: Методические указания; #538257
• страница: 2 из 3

Алгоритм Кемени – Снелла

Эвристический алгоритм Кемени – Снелла предназначен для определения результирующего ранжирования альтернатив. Реализуется алгоритм в несколько этапов.

1. 
   Исходя из частных ранжирований n альтернатив А₁, А₂, …, А_n определяются матрицы бинарных предпочтений (по каждому эксперту Э₁, Э₂, …, Э_m) с оценками :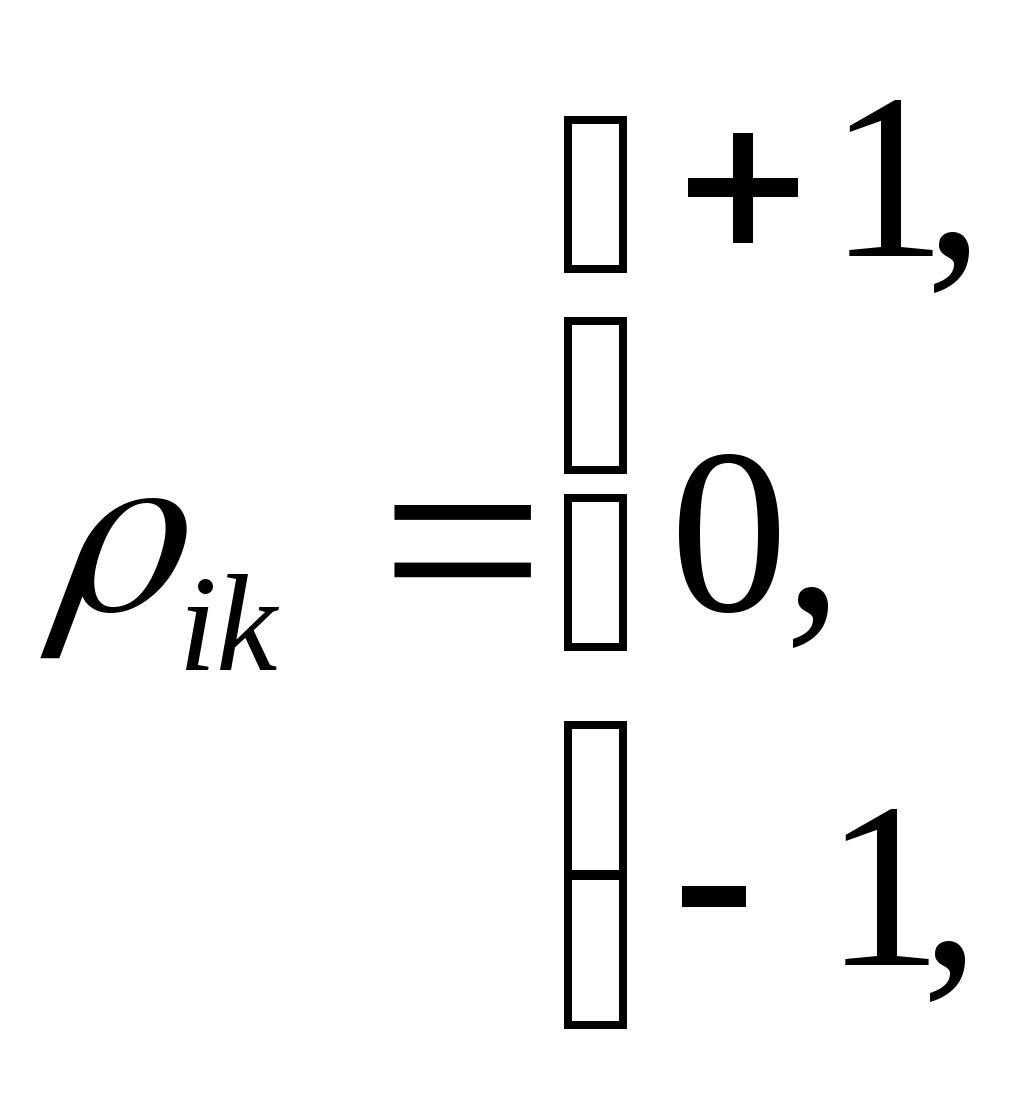
   

и ..

Например, известны частные ранжирования 8 экспертами 4 альтернатив (в экспертизе использован метод предпочтений):

Эj	Аi
	А1	А2	А3	А4
Э1	3	2	1	4
Э2	1	2	3	4
Э3	3	1	2	4
Э4	2	4	1	3
Э5	2	1	1	3
Э6	3	4	1	2
Э7	2	1	2	3
Э8	2	2	1	3

Исходя из указанных частных ранжирований, определяем матрицы бинарных предпочтений каждого эксперта с оценками .

Э1

А1

А2

А3

А4

Э2

А1

А2

А3

А4

Э3

А1

А2

А3

А4

Э4

А1

А2

А3

А4

А1

×

-1

-1

+1

А1

×

+1

+1

+1

А1

×

-1

-1

+1

А1

×

+1

-1

+1

А2

+1

×

-1

+1

А2

-1

×

+1

+1

А2

+1

×

+1

+1

А2

-1

×

-1

-1

А3

+1

+1

×

+1

А3

-1

-1

×

+1

А3

+1

-1

×

+1

А3

+1

+1

×

+1

А4

-1

-1

-1

×

А4

-1

-1

-1

×

А4

-1

-1

-1

×

А4

-1

+1

-1

×

Э5

А1

А2

А3

А4

Э6

А1

А2

А3

А4

Э7

А1

А2

А3

А4

Э8

А1

А2

А3

А4

А1

×

-1

-1

+1

А1

×

+1

-1

-1

А1

×

-1

0

+1

А1

×

0

-1

+1

А2

+1

×

0

+1

А2

-1

×

-1

-1

А2

+1

×

+1

+1

А2

0

×

-1

+1

А3

+1

0

×

+1

А3

+1

+1

×

+1

А3

0

-1

×

+1

А3

+1

+1

×

+1

А4

-1

-1

-1

×

А4

+1

+1

-1

×

А4

-1

-1

-1

×

А4

-1

-1

-1

×

2. 
   Определяется матрица потерь с оценками :
   

, .

По данным примера определим матрицу потерь с оценками :

Матрица потерь

	А1	А2	А3	А4
А1	×	9	13	2
А2	7	×	9	4
А3	3	7	×	0
А4	14	12	16	×

Например, элемент рассчитан следующим образом:

.

3. 
   Выполняется обработка матрицы потерь в несколько циклов. В каждом цикле рассчитываются суммы оценок потерь по строкам матрицы, находится альтернатива с минимальной суммой, которая исключается из матрицы потерь.
   

Выполним обработку матрицы потерь по данным примера:

Циклы вычислений	1	2	3
А1	24 (=9+13+2)	11 (=9+2) ←min А1 исключается из матрицы	-
А2	20 (=7+9+4)	11 (=7+4) ←min А2 исключается из матрицы	-
А3	10 (=3+7+0)←min А3исключается из матрицы	-	-
А4	42 (=14+12+16)	26 (=14+12)	0

4. 
   Находится результирующее ранжирование альтернатив (ранжирование определяется порядком исключения альтернатив из матрицы потерь).
   

Результирующее ранжирование альтернатив в примере получено таким: .