Методические указания по выполнению контрольной работы по дисциплине Теория принятия решений

• Название: Методические указания по выполнению контрольной работы по дисциплине Теория принятия решений
• Дата: 19.05.2022
• Размер: 314.5 Kb.
• Имя файла: Metod (1).doc
• Тип: Методические указания; #538257
• страница: 1 из 3

Лапченко Д.А. (моб. тел. [phone])

Методические указания

по выполнению контрольной работы по дисциплине

«Теория принятия решений»

для студентов заочной формы обучения
Задача 1. Обоснование решений в условиях риска

Суть статистического способа заключается в том, что изучается статистика потерь и прибылей, имевших место на данном или аналогичном производстве. Устанавливаются величина и частотность получения той, или иной экономической отдачи. На основе оставляется наиболее вероятный прогноз на будущее. Применительно к экономическим задачам методы теории вероятности сводятся к определению вероятности наступления событий и к выбору из возможных событий самого предпочтительного. Исходить следует из наибольшей величины математического ожидания, которое равно абсолютной величине этого события, умноженной на вероятность его наступления.

Главные инструменты статистического метода расчета экономического риска:

- вариация

- дисперсия

- стандартное (среднеквадратическое) отклонение.

Величина риска, или степень риска, может быть измерена двумя критериями: 1) среднее ожидаемое значение, 2) колеблемость (изменчивость) возможного результата.

Среднее ожидаемое значение – это то значение величины события, которое связано с неопределенной ситуацией. Оно является средневзвешенной всех возможных результатов, где вероятность каждого результата используется в качестве частоты, или веса, соответствующего значения. Таким образом, вычисляется предположительный результат.

В ситуации риска реализуется вероятностный подход, предполагающий прогнозирование возможных исходов и присвоение им соответствующих вероятностей. При этом пользуются:

• 
  известными, типовыми ситуациями;
  
• 
  предыдущими распределениями вероятностей на основании статистики предшествующих периодов или результатов выборочных обследований;
  
• 
  субъективными оценками, сделанными аналитиками, ЛПР самостоятельно или с привлечением экспертов.
  

Однако использование в качестве измерителей риска абсолютных показателей вариации не всегда является обоснованным. В частности необходимо сделать выбор наиболее рационального варианта из множества потенциально возможных решений. Возможность проведения сравнительной оценки вариантов решения дает относительный показатель вариации – коэффициент вариации ( ), который рассматривается в качестве показателя оценки степени риска. Чем больше значение коэффициента вариации, тем больше неопределенности для получения запланированного результата, и, следовательно, тем больше степень риска. Таким образом, рассматривая коэффициент вариации в качестве критерия обоснования решений в условиях риска, следует помнить, что этот критерий должен стремиться к минимуму:



Коэффициент вариации рассчитывается как отношение среднеквадратического отклонения (σ) к математическому ожиданию случайной величины (МО), выраженное в процентах:



Для интерпретации полученного значения коэффициента вариации может быть использована следующая шкала:

- малая степень риска;

- средняя степень риска;

- высокая степень риска.

Математическое ожидание случайной величины (например, ожидаемый размер прибыли) и среднеквадратическое отклонение могут быть рассчитаны следующим образом:

1. 
   Если имеется полная информация о распределении случайной величины, используют формулы: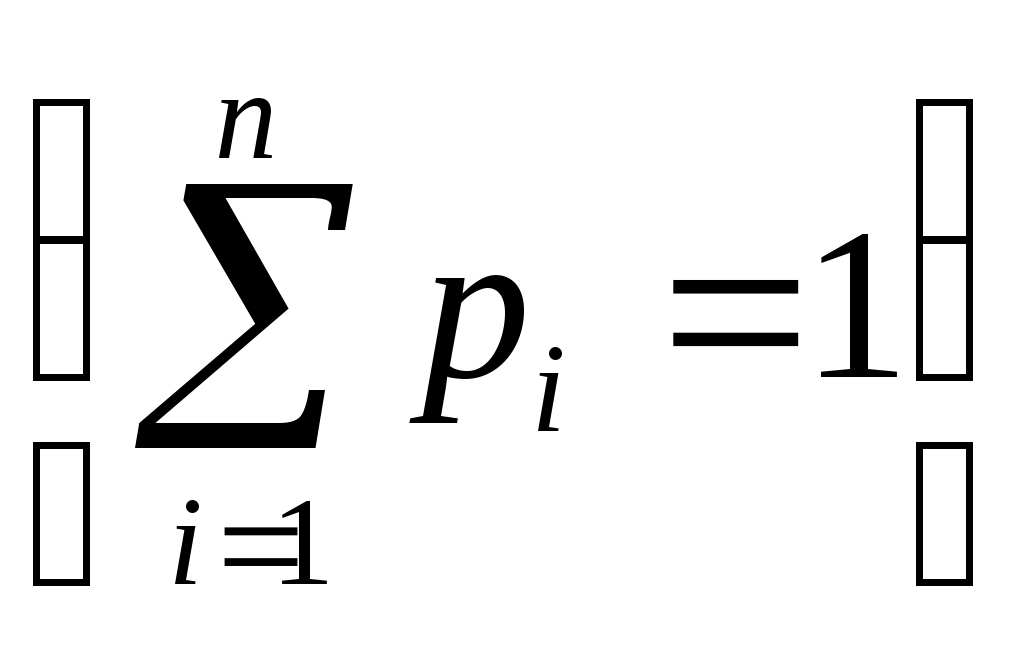
   

, ,

где x_i– прогнозная оценка случайной величины в i-м состоянии;

p_i – вероятность i-й прогнозной оценки;

.

2. 
   Если известны только размах вариации случайной величины (x_min и x_max) и соответствующие вероятности (p_min и p_max) – расчет производится на основе предположения о β-распределении случайной величины с использованием формул (p_min > p_max):
   

;

.

3. 
   Если известен только размах вариации (а вероятности не известны), то на основании предположения о β-распределении случайной величины величину отклонения можно оценить приближенно:
   

.

Задача 2. Обоснование решений в условиях неопределенности

Выбор рациональной альтернативы (стратегии) осуществляется с использованием различных критериев для оптимизации решений в условиях неопределенности.

Разработкой рекомендаций для выбора наилучшего варианта действий в условиях неопределенности занимается теория статистических решений. Эта математическая теория рассматривает игры с природой, в которых под природой понимаются объективные обстоятельства, внешняя среда. Считается, что природа сознательно не противодействует игроку. Условие задачи представлено в виде матрицы выигрышей (a_ji) игры с природой:

Матрица игры

Si xj	S1	S2	…	Sn
x1	a11	a12		a1n
x2	a21	a22		a2n
…	…
xm	am1	am2		amn

x_j – стратегии сознательного игрока, ;

S_i – состояния природы, ;

a_ji – выигрыш сознательного игрока при использовании им стратегии x_j, если состоянием природы будет S_i.

1. Критерий Лапласа.

Данный критерий предполагает равновероятность состояний внешней среды и рекомендует выбор стратегии с максимальным средним выигрышем:

К_Л = .

Вероятности состояний природы p_i равны между собой:

.

2. Критерий Байеса.

Этот критерий учитывает вероятности состояний природы и рекомендует выбор стратегии с максимальным среднеожидаемым выигрышем:

К_Б = , .

3. Критерий Вальда (максиминный критерий, критерий крайнего пессимизма, критерий наибольшей осторожности).

Данный критерий ориентируется на худшее состояние внешний среды и рекомендует выбор стратегии с максимальным гарантированным выигрышем в таких условиях:

К_В= .

4. Критерий Сэвиджа (минимаксного риска).

Критерий минимаксного риска ориентируется на самую неблагоприятную обстановку и рекомендует выбор стратегии с минимальным риском:

К_С = .

Для использования данного критерия необходимо перейти от матрицы выигрышей к матрице рисков.

Риск (r_ji) – разность между выигрышем, который игрок получил бы, если бы он знал, что состоянием природы будет состояние S_i, и выигрышем, который игрок получит, не имея этой информации при использовании стратегии x_j:

, (при заданном i).

5. Критерий Гурвица (компромиссный критерий, критерий пессимизма-оптимизма).

Этот критерий учитывает индивидуальные предпочтения сознательного игрока к пессимизму и оптимизму. Для его использования необходимо задать значение коэффициента пессимизма α, α [0,1]:

К_Г = .

Возможны следующие характерные случаи использования критерия Гурвица:

1. 
   если  = 1, то
   

К_Г¹ = .

В этом частном случае критерий Гурвица совпадает с критерием Вальда (крайнего пессимизма).

2. 
   если  = 0, то
   

К_Г⁰ = .

В этом частном случае критерий Гурвица совпадает с критерием крайнего оптимизма.

3. 
   если  = 0,5, то
   

К_Г^0,5 = .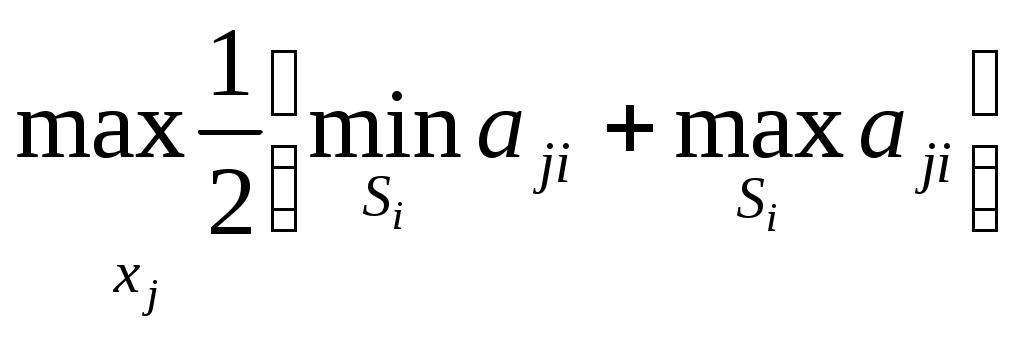
Задача 3. Обоснование решений в условиях многовариантности и

многокритериальности

Для выполнения задачи 3 расчетной части контрольной работы студентам необходимо применить один из методов экспертного или системного анализа для обоснования управленческих решений. Описания некоторых процедур обоснования решений приведены ниже.
Определение множества Эджворта - Парето

В основе определения множества Эджворта - Парето лежит принцип согласованного оптимума. Согласно данному принципу оптимизация систем по одному из критериев практически исключает возможность оптимизации по другим критериям, т.е. возможна оптимизация систем по многим, часто противоречивым критериям.

Парето оптимальные решения – это такие перспективные компромиссные решения, которые не обеспечивают оптимум по каждому из частных критериев, однако являются удовлетворительными на множестве критериев, причем улучшение состояния по любому из критериев приводит к ухудшению состояния по другим критериям.

Альтернативы относятся к множеству Эджворта - Парето, если каждая из них превосходит любую другую по какому-то из критериев. Такие альтернативы принято называть несравнимыми. Их действительно невозможно сравнить непосредственно на основе критериальных оценок. Но если решение должно быть принято, то сравнение альтернатов, принадлежащих множеству Эджворта - Парето, возможно на основе дополнительной информации о системе предпочтений лица, принимающего решение (ЛПР), на множестве частных критериев. Множество Эджворта - Парето включает в себя наиболее «контрастные» альтернативы, сложные для сравнения. Если стоит задача выбора одной лучшей альтернативы, то она обязательно принадлежит данному множеству.

Один из возможных способов решения задачи определения множества Эджворта - Парето состоит в попарном сравнении альтернатив и исключении доминируемых. Если одна альтернатива лучше другой по всем или хотя бы по одному из критериев, а по другим критериям не уступает, то эта другая альтернатива исключается из рассмотрения (не включается во множество).
Метод ранга (балльных оценок). Оценка качества экспертизы

Пусть имеется m экспертов Э₁, Э₂, …, Э_m и n альтернатив А₁, А₂, …, А_n. Каждый эксперт оценивает важность альтернатив, пользуясь некоторой балльной шкалой оценок (например, 10-, 12-, 100-балльные шкалы). В этих условиях веса альтернатив определяются следующим образом:

1. 
   Составляется исходная матрица предпочтений с оценками ρ_ji:
   

	А1	А2	…	Аn
Э1	ρ11	ρ12	…	ρ1n
Э2	ρ21	ρ22	…	ρ2n
…	…	…	…	…
Эm	ρm1	ρm2	…	ρmn

0 ≤ ρ_ji≤ К; К=10, 12, 100 – в зависимости от используемой шкалы, j = ; i = .

2. 
   Вычисляются искомые веса альтернатив:
   

ω_i = ; .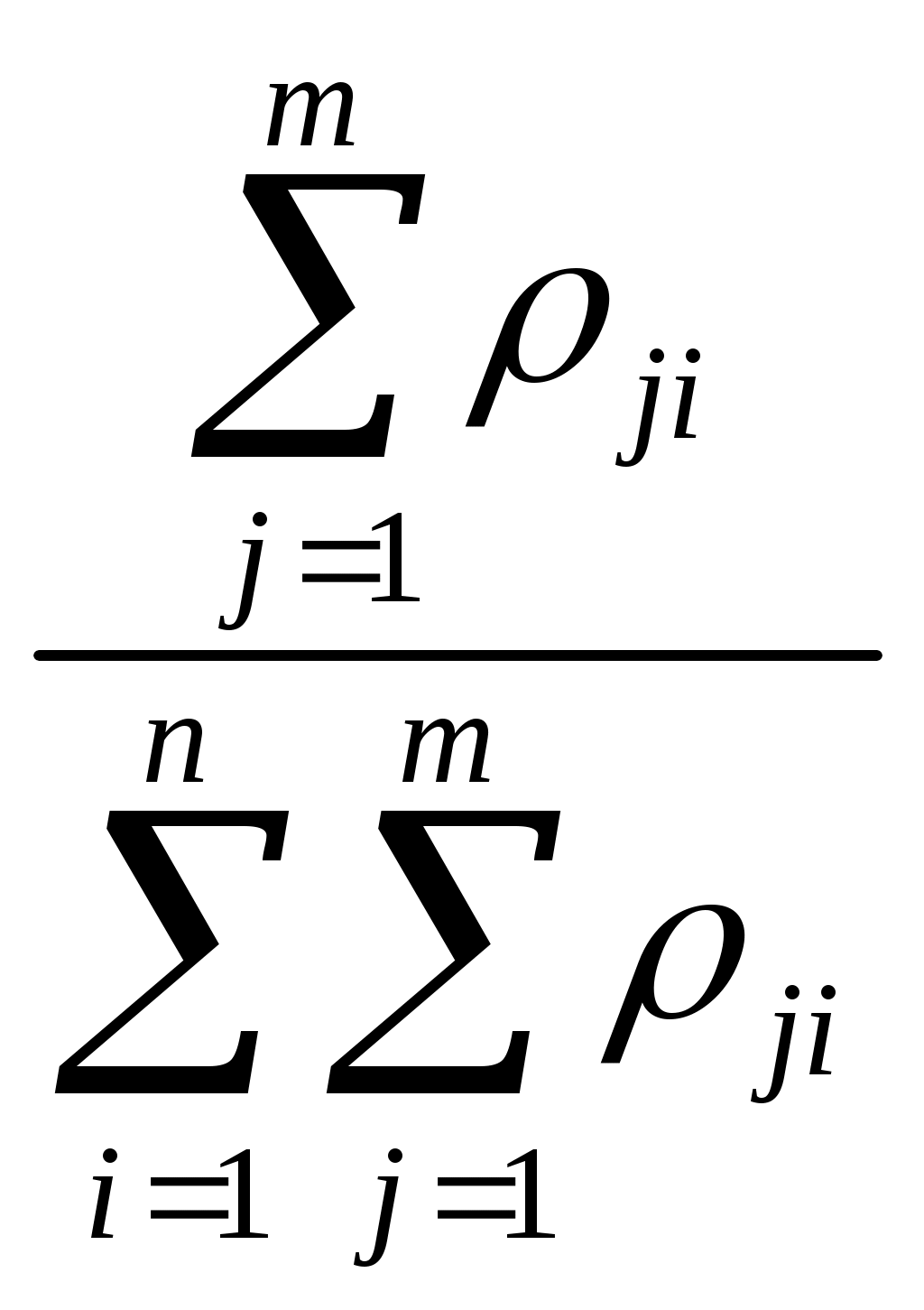

Для оценки качества экспертизы, проведенной с использованием метода ранга, могут быть рассчитаны дисперсии:

1. 
   дисперсии, характеризующие близость суждений каждого отдельного эксперта с коллективным суждением группы экспертов –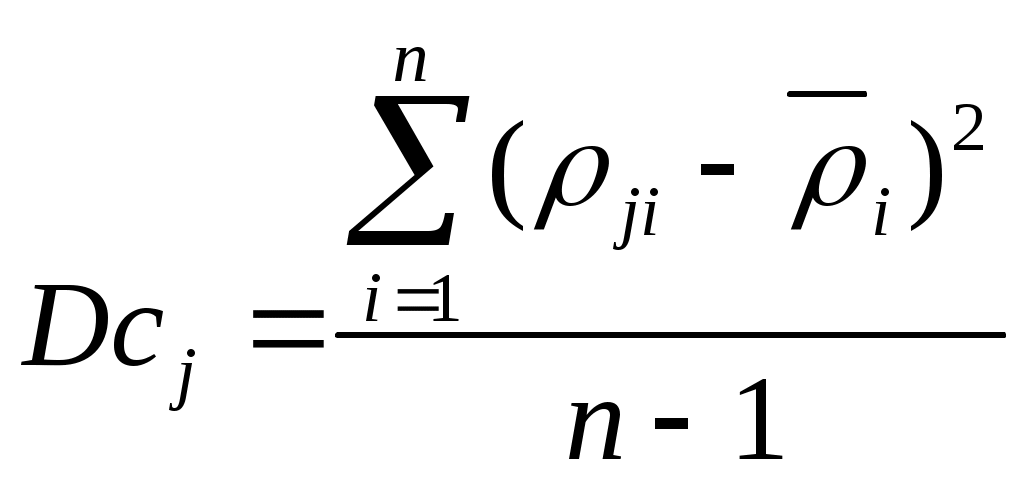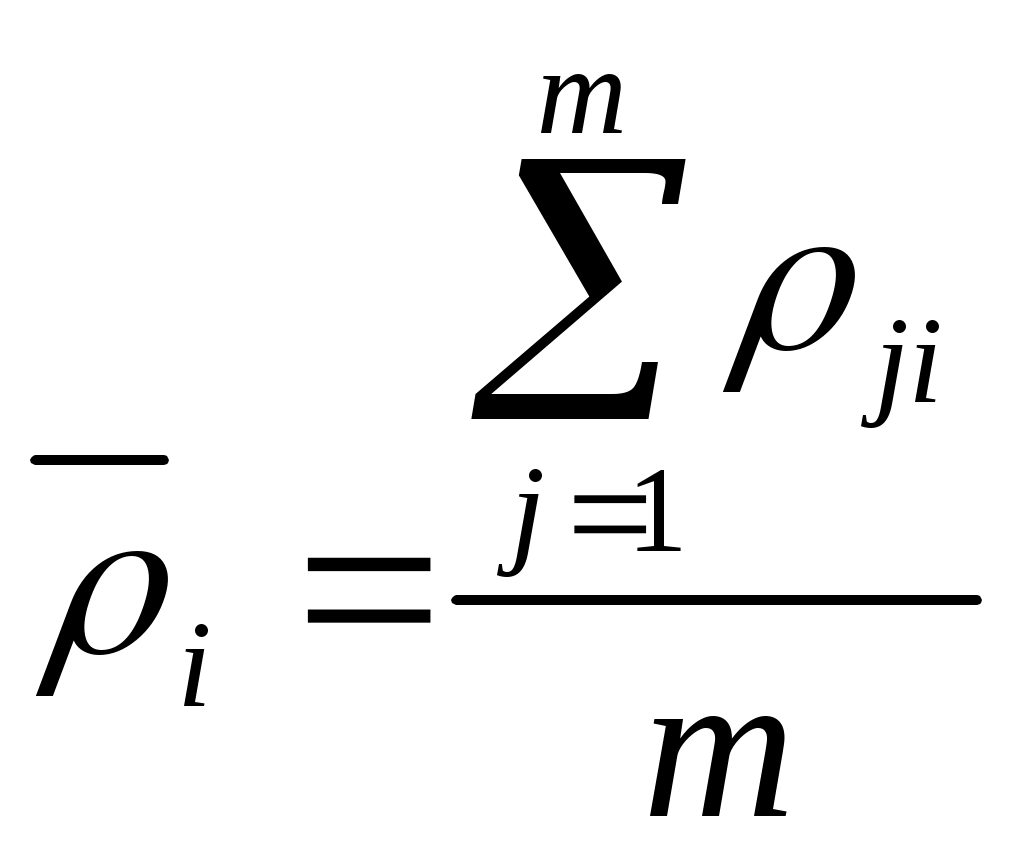
   

, ;

2. 
   дисперсии, характеризующие согласованность экспертов при оценке каждой альтернативы –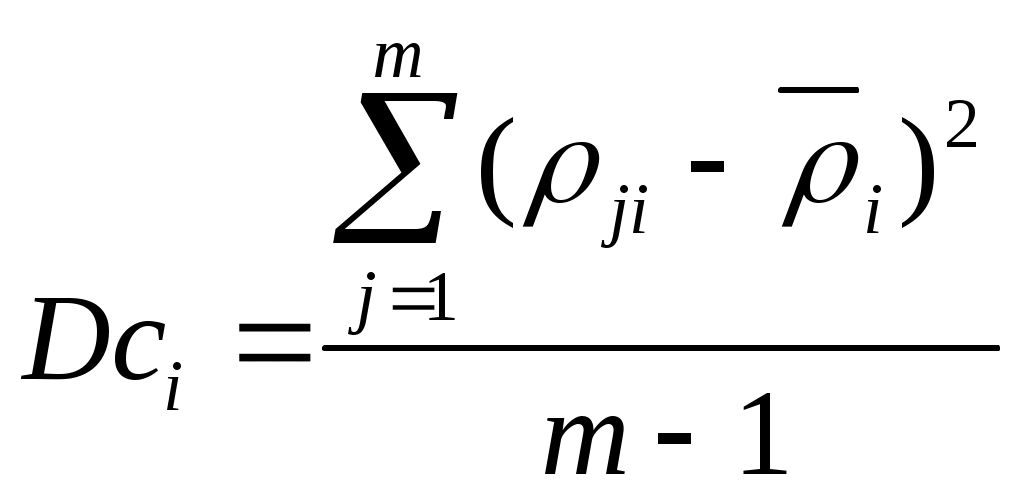
   

.

Чем меньше величина дисперсии, тем больше степень согласованности и меньше разброс мнений.
Метод предпочтений. Оценка согласованности экспертов

Пусть имеется m экспертов Э₁, Э₂, …, Э_m и n альтернатив А₁, А₂, …, А_n. Каждый эксперт оценивает важность альтернатив, пользуясь числами натурального ряда, причем наиболее важной альтернативе присваивается 1, следующей по важности -2 и т.д. В этих условиях веса альтернатив определяются следующим образом:

3. 
   Составляется исходная матрица предпочтений с оценками K_ji:
   

	А1	А2	…	Аn
Э1	K11	K12	…	K1n
Э2	K21	K22	…	K2n
…	…	…	…	…
Эm	Km1	Km2	…	Kmn

1 ≤ K_ji≤ n; j = ; i = .

4. 
   Составляется модифицированная матрица предпочтений с оценками:
   

K^/_ji = n - K_ji.

5. 
   Находятся суммарные оценки предпочтений альтернатив:
   

K_i = .

6. 
   Вычисляются искомые веса альтернатив:
   

ω_i = ; .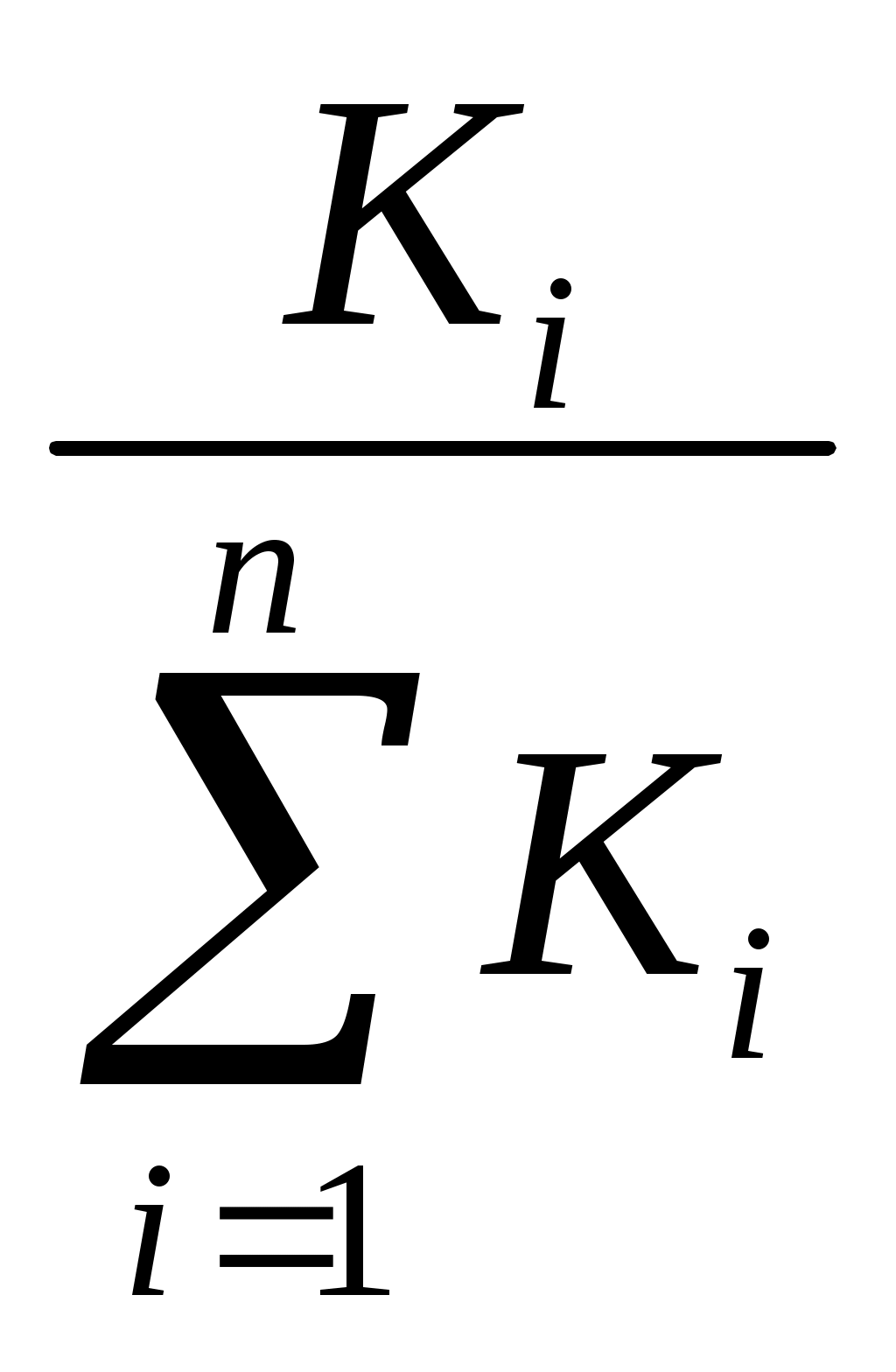

Для оценки согласованности экспертов используется коэффициент конкордации Кендалла:

W = , .

Согласованность считается достигнутой, если значение коэффициента конкордации больше 0,5.

Расчет коэффициента производится следующим образом:

• 
  находится вспомогательная величина:
  

А = ;

• 
  определяется разности значений по каждой альтернативе:
  

R_i = S_i – A,

где S_i– сумма оценок по каждой альтернативе на основе исходной матрицы предпочтений;

• 
  находится сумма квадратов разностей:
  

S = ∑ R_i².
Метод парных сравнений

Экспертам предлагается произвести сравнение n альтернатив А₁, А₂, …, А_n попарно, с тем, чтобы установить наиболее значимую в каждой паре. Для облегчения этой процедуры составляют матрицы парных сравнений, в которых все сопоставляемые альтернативы записываются дважды: по горизонтали и по вертикали. Каждый эксперт, заполняющий такую матрицу, должен проставить на пересечении сравниваемых альтернатив оценку 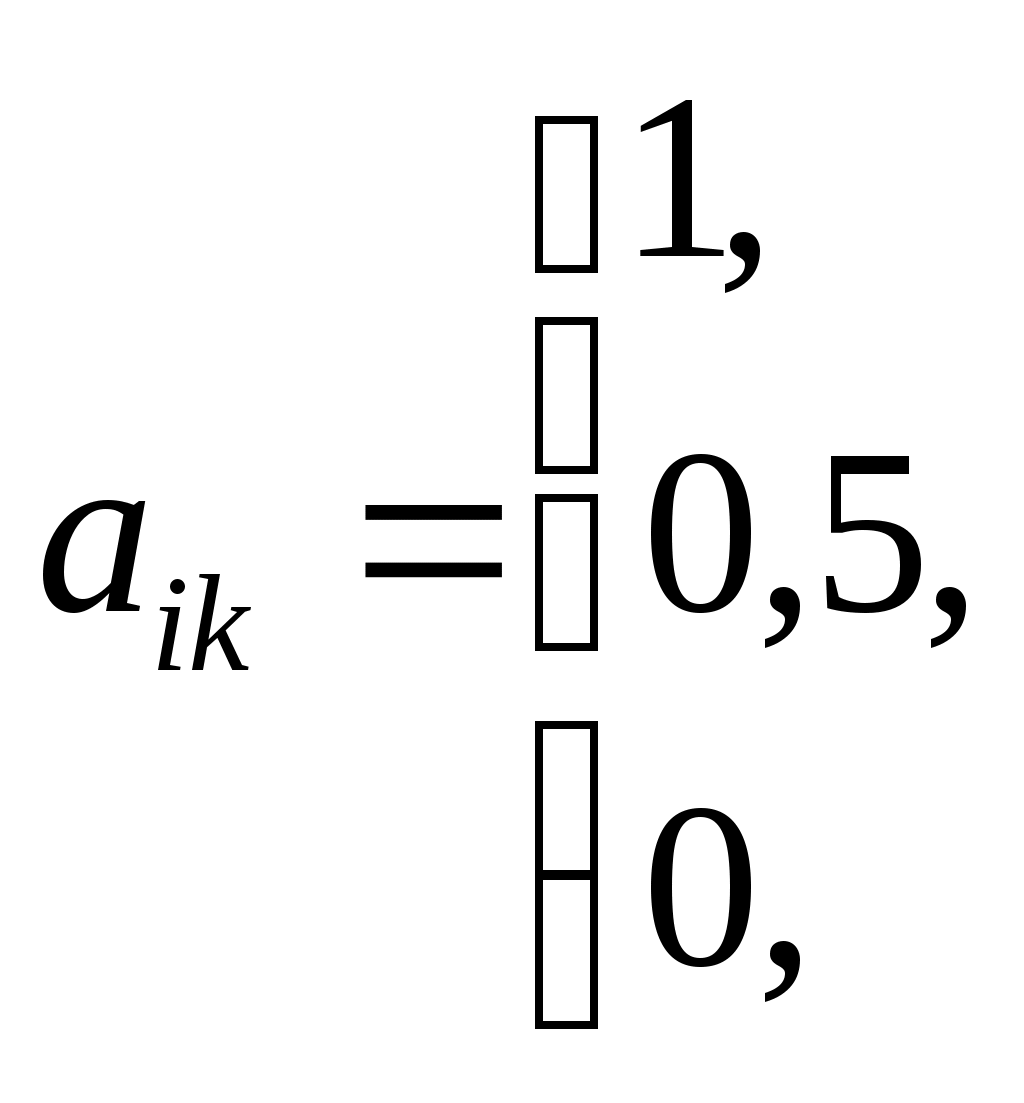с использованием определенной шкалы, например:

и .

Матрица парных сравнений

	А1	А2	…	Аn
А1	×	a12	…	a1n
А2	a21	×	…	a2n
…	…	…	…	…
Аn	an1	an2	…	×

Если процедура сравнения выполняется несколькими экспертами, то в результате сложения одноименных элементов частных матриц составляется суммарная матрица, отражающая предпочтения всех экспертов.

В таких условиях веса альтернатив определяются следующим образом:

• 
  определяется цена каждой альтернативы как сумма оценок по строке матрицы –
  

;

• 
  вычисляются искомые веса альтернатив путем нормирования цен альтернатив –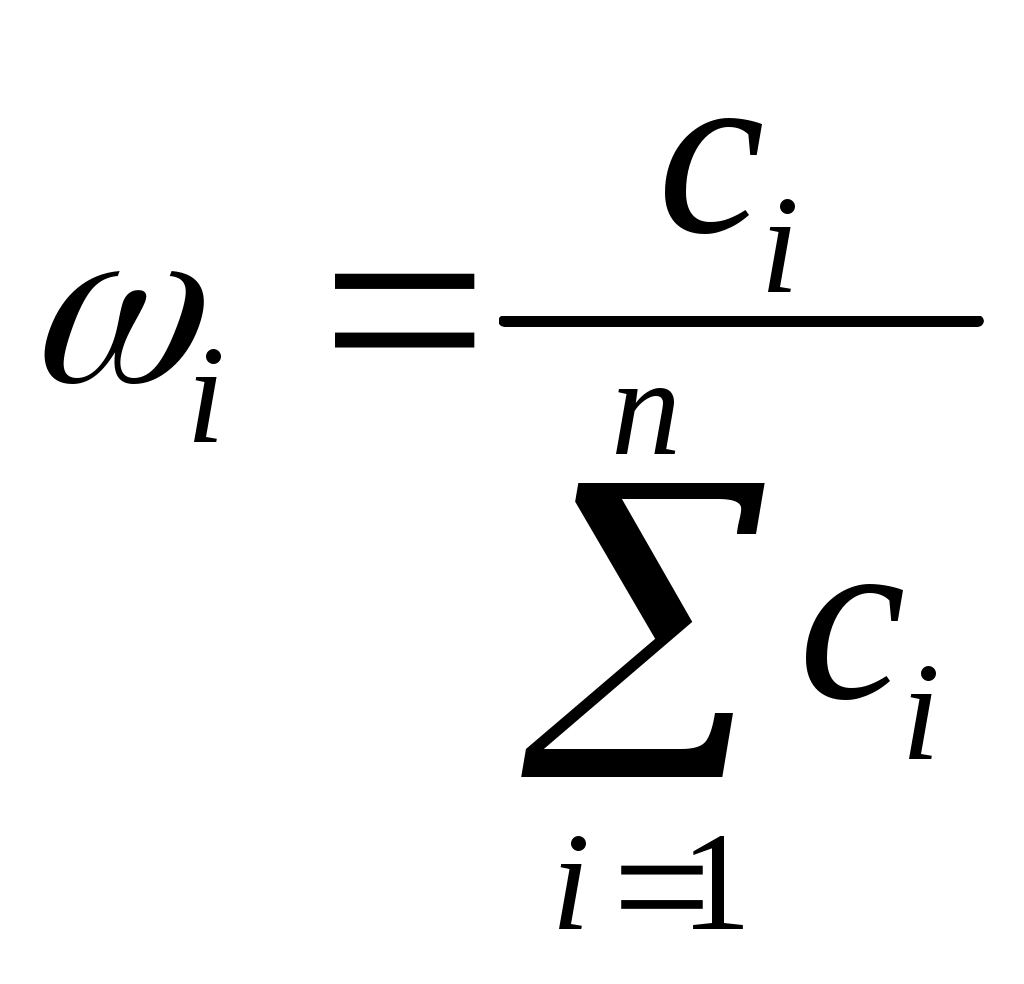
  

, .