Методические указания по выполнению курсовой работы для студентов всех форм обучения. Лысьва, 2016, 28 с
 Скачать 1.19 Mb. Скачать 1.19 Mb.
|
|
М Федеральное государственное бюджетное образовательное учреждение высшего образования Пермский национальный исследовательский политехнический университет Лысьвенский филиал Кафедра естественнонаучных дисциплин УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ «Теория автоматического управления» основной образовательной программы подготовки бакалавров по направлению 13.03.02 «Электроэнергетика и электротехника» МЕТОДИЧЕСКИЕ УКАЗАНИЯ по выполнению курсовой работы Лысьва, 2016 Разработчик-составитель доцент Лопатин В.Г. Рецензент д.т.н., профессор В.П. Казанцев. Учебно-методический комплекс дисциплины «Теория автоматического управления» основной образовательной программы подготовки бакалавров по направлению 13.03.02 «Электроэнергетика и электротехника». Методические указания по выполнению курсовой работы для студентов всех форм обучения. Лысьва, 2016, – 28 с. Методические указания рассмотрены и одобрены на заседании кафедры ЕН « 14 » сентября 2016 г, протокол № 2. Лысьвенский филиал Пермский национальный исследовательский политехнический университет, 2016 г. содержание
ВВЕДЕНИЕ Предполагается, что к моменту начала выполнения курсовой работы студент твердо усвоил необходимые теоретические знания. Консультации руководителя курсовой работы служат для текущего контроля выполнения расчетов и, при необходимости, их коррекции. Цель выполнения работы: углубление знаний основных разделов ТАУ, ознакомление с методами исследования и проектирования систем автоматического управления (САУ) с заданными параметрами и получение практических навыков автоматизированного проектирования и исследования систем регулирования с применением персональных компьютеров. Задачи, решаемые в процессе выполнения курсовой работы: - ознакомление с математическим описанием систем управления; - изучение процедуры синтеза систем регулирования, базирующейся на принципах подчиненного регулирования координат; - получение практических навыков проектирования типовых структур управления; - приобретение практических навыков работы с компьютерной системой автоматизированного проектирования и исследования объектами управления. Порядок выполнения курсовой работы: - ознакомление с заданием на курсовую работу (вариант задает преподаватель); - ознакомление с математическим описанием и процедурой синтеза САУ; - преобразование структурной схемы с использованием пакета Microsoft Office Visio и определение передаточной функции разомкнутой системы; - определение устойчивости системы по характеристикам, построенным с использованием пакета Matlab. В методических указаниях кроме задания и примера выполнения, дается небольшой объем теоретического материала, способствующего наиболее быстрому вхождению в курс решаемых вопросов, однако наличие этого материала не исключает пользование справочной, научной и учебной литературой. Курсовые работы выполняются в соответствии с требованиями, сформированными на основании ГОСТ 7.32 – 2001, и сопровождаются ясным текстом, поясняющими рисунками и схемами. Небрежно выполненные работы не принимаются. Курсовые работы сдаются преподавателю для оценки не позднее, чем за месяц до экзаменов. Окончательная оценка выставляется после защиты курсовой работы. Все рисунки и графики выполняются четко на миллиметровой бумаге или на листах формата А4 с использованием прикладного программного обеспечения. 1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ По заданной системе дифференциальных уравнений, описывающих работу САУ необходимо: Составить структурную схему САУ; Найти передаточную функцию разомкнутой системы на основе использования правил структурных преобразований Построить асимптотическую ЛАЧХ, ЛФЧХ и АФХ разомкнутой САУ; Определить устойчивость замкнутой САУ; найти предельный коэффициент усиления; Определить статическую и кинетическую ошибки замкнутой системы. Сделать выводы о результатах проделанной работы. Для определения передаточной функции разомкнутой системы, структурную схему, составленную на основе заданной системы дифференциальных уравнений, следует привести к одноконтурной системе (к виду аналогичному, представленному на рис. 2, г). Если САУ при заданном коэффициенте усиления окажется неустойчивой, то статическую и кинетическую ошибки следует определять для системы с коэффициентом усиления в 2 раза меньше предельного. К оформлению расчетного задания предъявляются следующие требования: 1) На титульном листе указываются: тема расчетного задания, номер варианта, фамилия и инициалы студента и преподавателя, год выполнения (см. пример оформления на последней странице). 2) Выполненная курсовая работа оформляется на отдельных листах формата А4. Поля: сверху, снизу, слева – 20 мм, справа – 10 мм. Межстрочный интервал в тексте – 1,5. Межстрочный интервал в заголовке (если больше 1 строки) – 1,0. Интервал после заголовка 12 пт. По тексту работы установить интервал «перед» и «после» – 0 пт. Шрифт – Times New Roman, 14 пт., обычный. Подчеркивание в тексте не допускается. Отступ –1,25. Использовать клавиши «Tab» и «Enter». Не допускается повышенная разряженность в последней строке абзаца. Для исключения этой ошибки следует использовать клавишу «Enter». Нумерация страниц – по центру снизу. Расположение текста на странице – по ширине. Расположение заголовков – по центру. Полужирное выделение допускается для заголовков и, в порядке исключения, для ключевых понятий в тексте. Таковых на 1 странице не должно быть больше 4-5. Любые сокращения или аббревиатуры сначала должны быть полностью названы и обозначены. Только после этого ими можно пользоваться в тексте работы. Названия рисунка пишется снизу рисунка. Расположение названия – по центру. Для названия рисунка использовать шрифт «курсив». Текст в оформляется шрифтом 12. Нумерация рисунков – сквозная. Название таблицы пишется сверху таблицы. Расположение названия – справа. Для названия таблиц использовать шрифт «курсив». Текст в таблицах оформляется шрифтом 12 с межстрочным интервалом – одинарный. Нумерация таблиц – сквозная. Каждый новый раздел (но не параграф!!!) следует начинать с новой страницы. Не допускать пустых!!! листов в тексте, когда на странице всего 2-3 строки. В этом случае нужно отредактировать текст таким образом, чтобы исключить эту ситуацию. Последний лист раздела должен быть заполнен, минимум, на 50÷75%. При использовании литературы должна быть дана ссылка на литературный источник, откуда она взята. 3) Рисунки должны выполняются с помощью прикладных программ, а если вручную, то линеек, лекал и могут располагаться как по тексту, так и в конце. Рисунки должны иметь сквозную нумерацию со ссылками в тексте. 2. ПРИМЕР ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ Работа системы автоматического управления задана системой дифференциальных уравнений:   Решение Составим структурную схему САУ. Перепишем в операторной форме исходную систему дифференциальных уравнений, приняв начальные условия нулевыми: 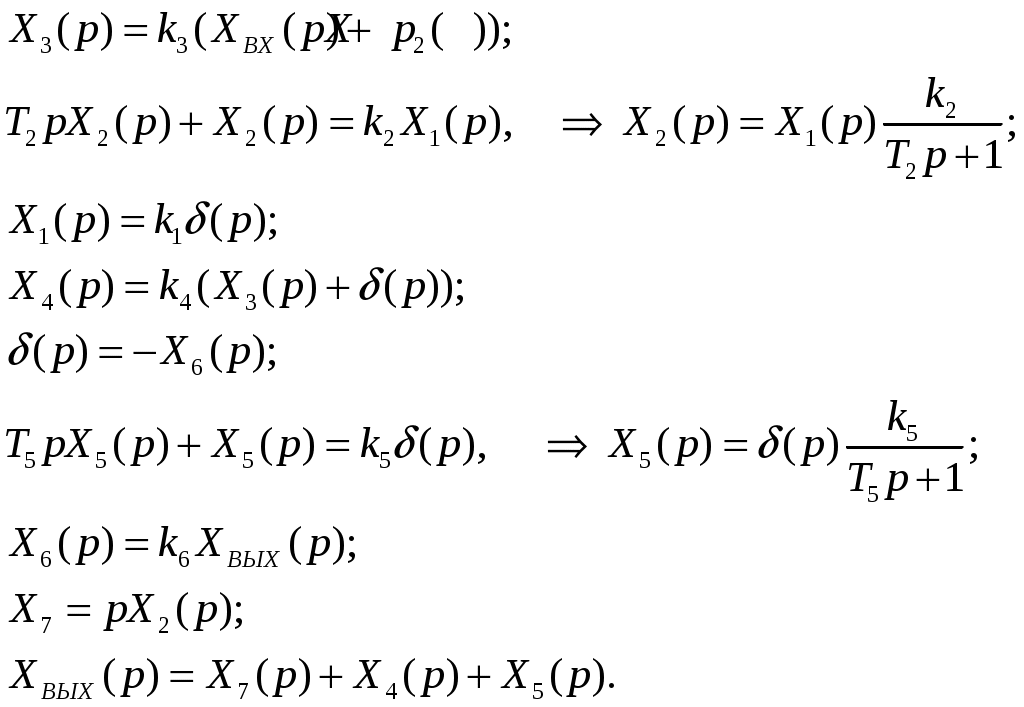 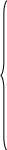 Полученной схеме уравнений соответствует структурная схема, представленная на рис. 1. 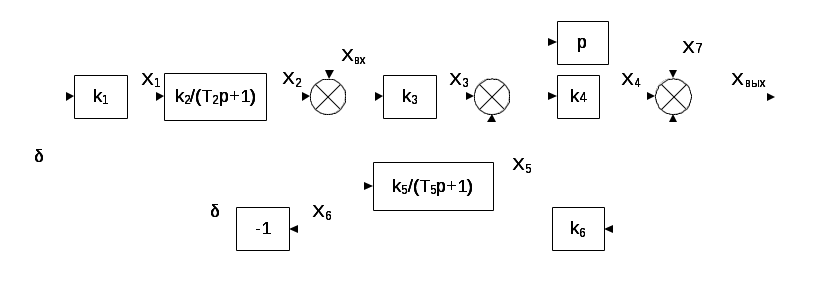 Рисунок 1. Структурная схема САУ 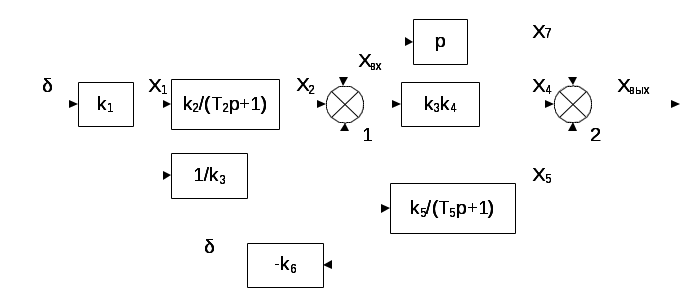 Рисунок 2 а. Преобразование исходной схемы САУ. 1-й этап 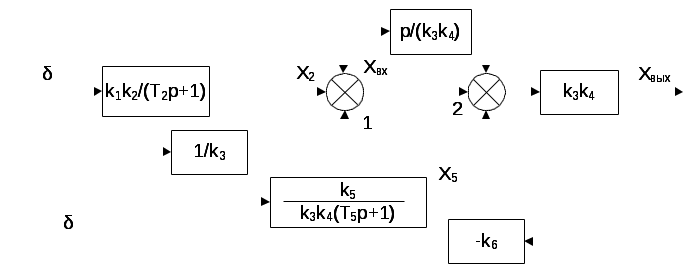 Рисунок 2 б. Преобразование исходной схемы САУ. 2-й этап 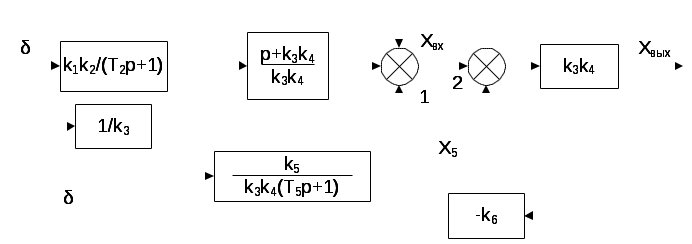 Рисунок 2 в. Преобразование исходной схемы САУ. 3-й этап 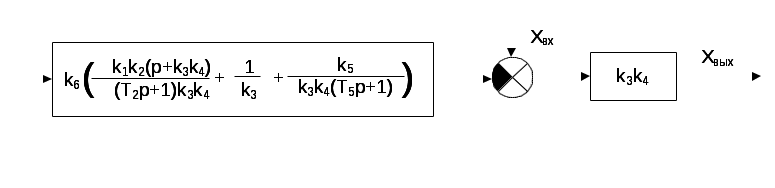   Рисунок 2 г. Преобразование исходной схемы САУ. 4-й этап Для нахождения передаточной функции системы 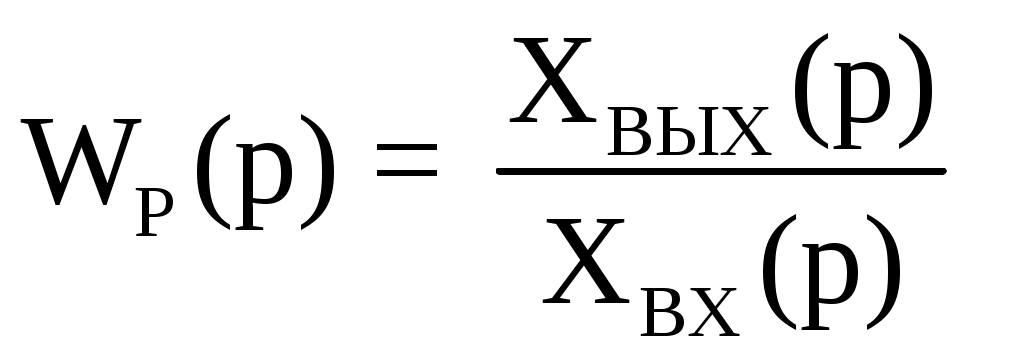 преобразуем структурную схему САУ, изображенную на рис. 1. Для этого используем известные правила структурных преобразований. Последовательность преобразований показана (рис. 2, а, б, в, г). Затем разорвем обратную связь. Тогда искомая передаточная функция разомкнутой системы будет равна: преобразуем структурную схему САУ, изображенную на рис. 1. Для этого используем известные правила структурных преобразований. Последовательность преобразований показана (рис. 2, а, б, в, г). Затем разорвем обратную связь. Тогда искомая передаточная функция разомкнутой системы будет равна: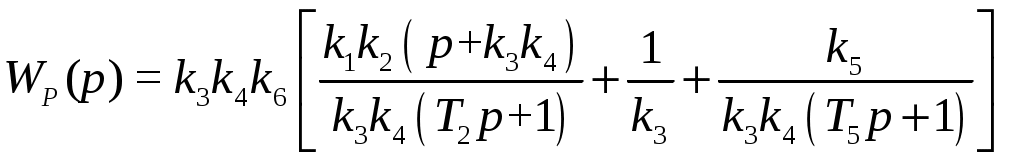 После подстановки в выражение WP(p) численных значений параметров, получим: 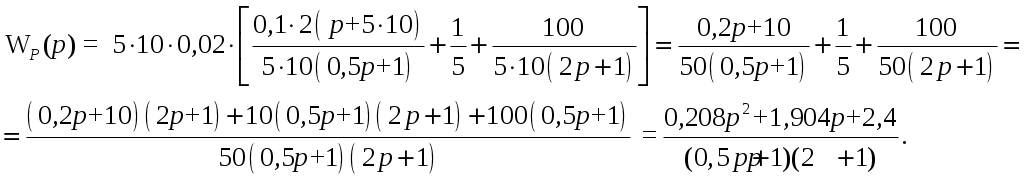 (1) (1)Затем в числителе желательно получить коэффициент при р0 равным единице. Для этого вынесем значение 2,4 за скобки. 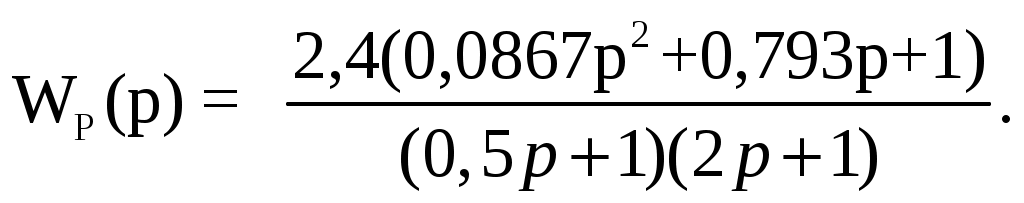 Решим полученное в числителе квадратное уравнение в скобках 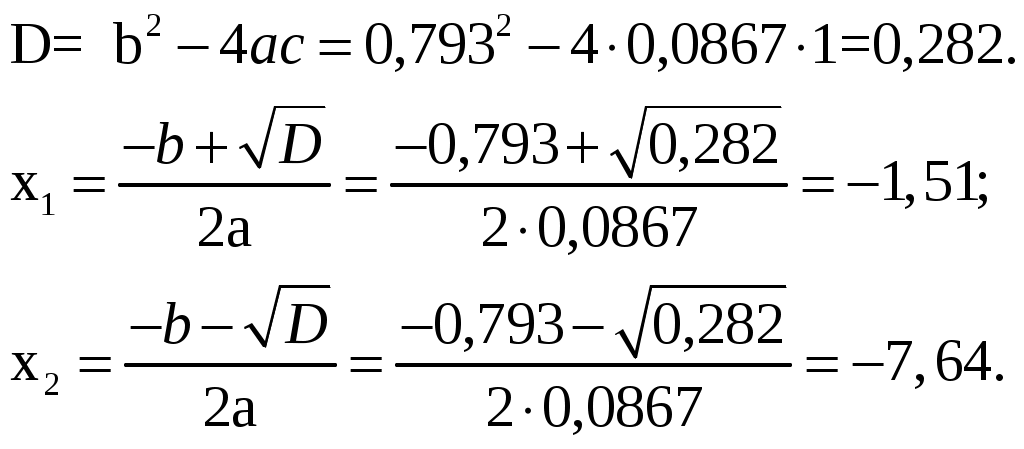 Выполним замену х → р, т.к. в передаточной функции используется параметр р, и, исходя из соотношения Для получения в передаточной функции числителя коэффициента при р0 равного единице с тем чтобы с = 1 преобразуем числитель следующим образом: 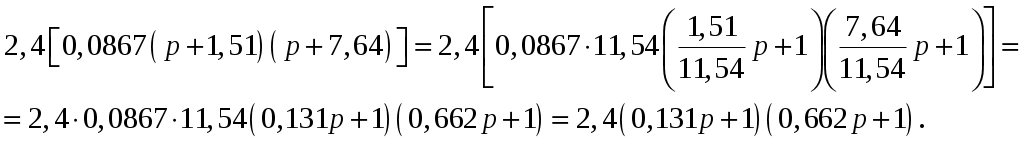 В результате получим удобное выражение преобразованной передаточной функции WP(p), в котором при каждом коэффициенте р0 стоит 1 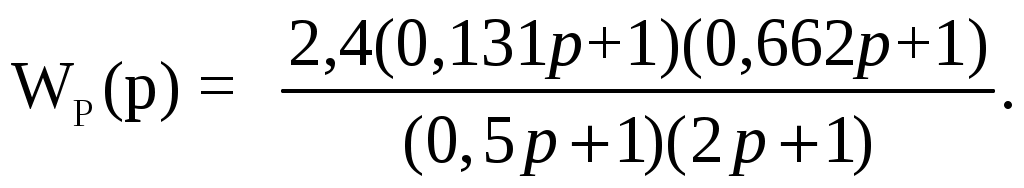 Для построения ЛАЧХ, ЛФЧХ и АФХ разомкнутой САУ запишем выражения для: а) комплексного коэффициента усиления: 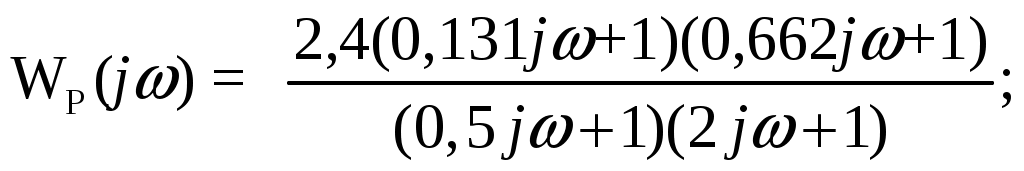 б) амплитудно–частотной характеристики: 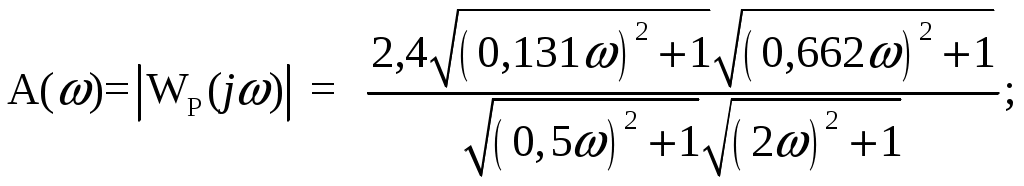 в) фазо–частотной характеристики: г) логарифмической амплитудно-частотной характеристики: 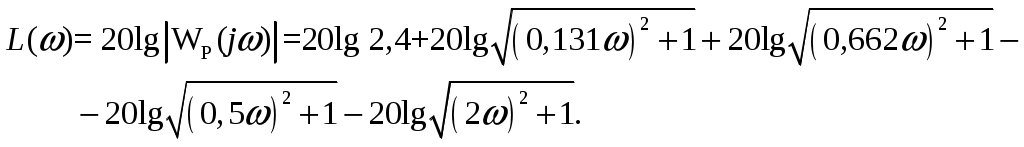 Асимптотическая ЛАЧХ и соответствующая ей ЛФЧХ представлены на рис.3. Их можно построить с помощью графического редактора Excel, с помощью пакета MathCAD. Универсальным средством для моделирования систем является пакет прикладных программ для решения задач технических вычислений Matlab. Воспользуемся функцией Marginиз данного пакета для расчета и построения ЛАЧХ и ЛФЧХ в виде диаграммы Боде с одновременным определением относительной устойчивости системы. Запишем скрипт Matlab >> num=[0.208 1.904 2.4]; den=[1 2.5 1]; >> sys=tf(num, den) Transfer function: 0.208 s^2 + 1.904 s + 2.4 ------------------------- s^2 + 2.5 s + 1 >> margin(sys) 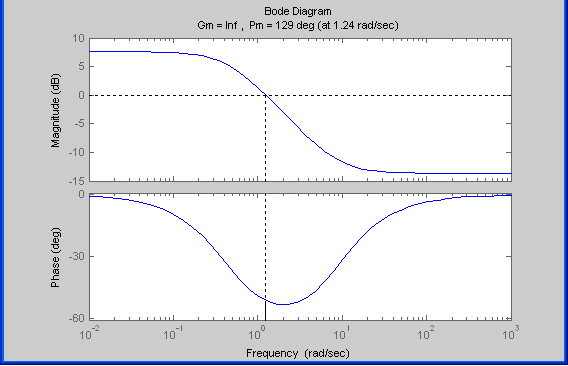 Рисунок 3. ЛАЧХ и ЛФЧХ – диаграмма Боде с показателями относительной устойчивости 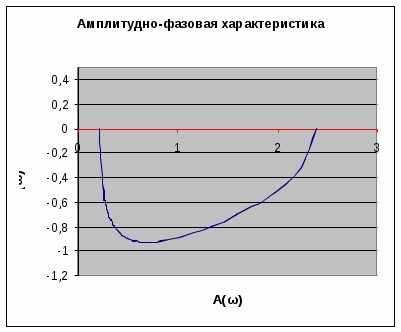 Рисунок 4. АФХ разомкнутой системы Построение амплитудно-фазовых характеристик Определение динамических свойств элементарных звеньев производится по амплитудно-фазовой характеристике (АФХ) W(jω) = R(ω) + jΙm(ω) = A(ω)ejφ(ω) , где R(ω) – вещественная часть амплитудно-фазовой характеристики (ВЧХ); Ι(ω) – мнимая часть амплитудно-фазовой характеристики (МЧХ); A(ω) – амплитудная характеристика; φ(ω) – фазовая характеристика. Амплитудно-фазовую характеристику можно построить в прямоугольной системе координат по значениям R(ω) и Ιm(ω). Для этого для каждого значения ω определяется R(ω) и откладывается по оси абсцисс, затем определяется Ιm(ω) и откладывается по оси ординат. Полученные точки с координатами (R(ω); Ιm(ω)) соединяются плавной кривой, которая и будет АФХ. Построить АФХ можно в полярных координатах по значению φ(ω) и A(ω). Для этого для каждого значения частоты ω определяется угол сдвига фаз φ(ω) и откладывается от вектора R(ω). Затем определяется A(ω) и откладывается на луче с заданным φ(ω). Данные расчета помещены в табл. 11. Полученные точки соединяются плавной кривой, которая и будет амплитудно-фазовой характеристикой. АФХ разомкнутой системы представлена на рис. 4. 5. Определим устойчивость замкнутой САУ. По критерию Найквиста определяем устойчивость разомкнутой системы, а по корням характеристического полинома устойчивость замкнутой системы. Таблица 11
Критерий Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике разомкнутого контура системы. Построим диаграмму Найквиста с использованием функции nyquist системы программирования Matlab. Для этого возьмем передаточную функцию разомкнутой САУ, представленную в уравнении (1) Передаточная функция замкнутой САУ: 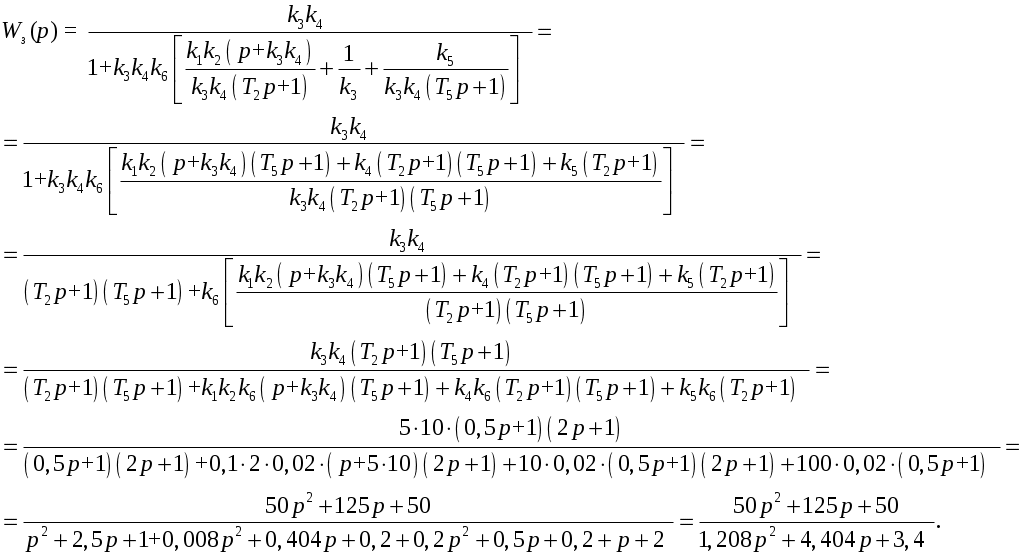 (2) (2)Запишем скрипт Matlab с переменными num и den для разомкнутой САУ и numz и denz для замкнутой САУ соответственно: >> num=[0.208 1.904 2.4]; den=[1 2.5 1];numz=[50 125 50]; denz=[1.208 4.404 3.4]; >> sys=tf(num, den); >> roots(den) ans = -2.0000 -0.5000 >> roots(denz) ans = -2.5357 -1.1100. >> nyquist (sys). Команда roots(den) возвращает значения корней разомкнутой САУ, а команда roots(denz) определяет значения корней замкнутой САУ. Как видим, все корни замкнутой САУ имеют отрицательные вещественные части, а значит, система устойчива. На рис. 5 приведена диаграмма Найквиста, которая, как видим, не охватывает точку (-1; j0) комплексной плоскости. Это позволяет говорить об устойчивости замкнутой САУ без нахождения корней характеристического уравнения. Поскольку функция nyquist применена без указания параметров, то диаграмма строится автоматически для всего диапазона регулирования частоты ω (–; +) и полный годограф Найквиста симметричен относительно действительной оси. 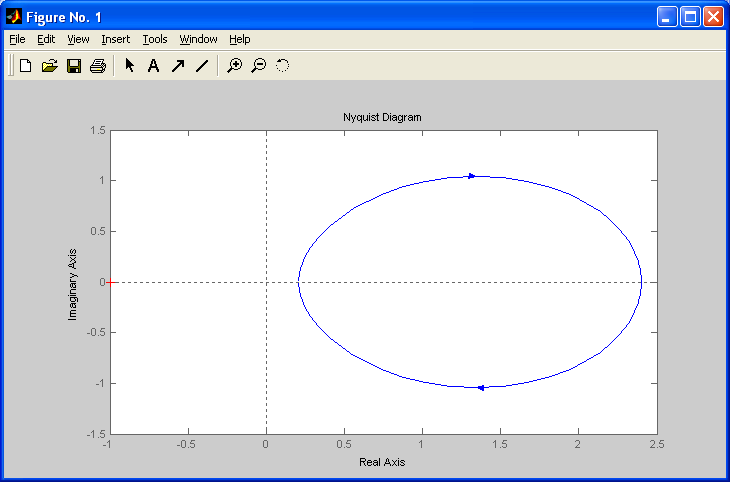 Рисунок5 Годограф Найквиста разомкнутой САУ По критерию Гурвица: для этого передаточную функцию замкнутой САУ (2): 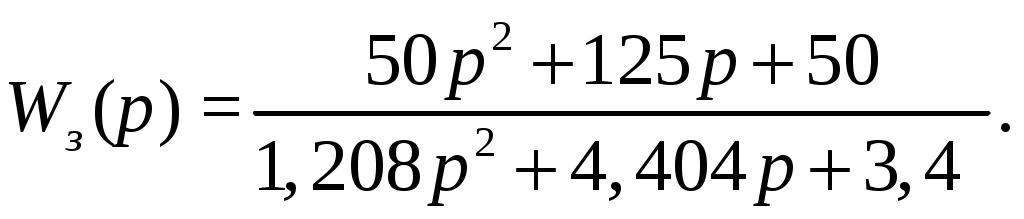 Составим определители Гурвица из коэффициентов характеристического полинома замкнутой системы 2-го порядка: 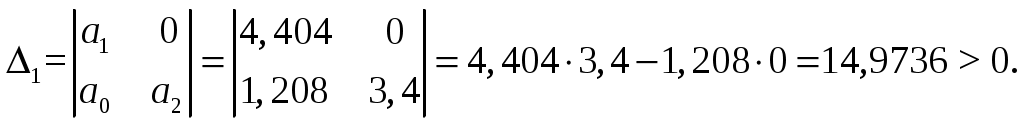 Определитель положительный при положительном коэффициенте а0, следовательно, замкнутая система устойчива. Все корни характеристического полинома имеют отрицательную действительную часть, следовательно, в соответствии с необходимым и достаточным условием устойчивости, замкнутая система неустойчива. 6. Проверим полученный результат с помощью системы программирования Matlab, непосредственно вычислив корни характеристического уравнения: замкнутой системы. Для этого воспользуемся функцией «pole». Ниже приведен скрипт и результат вычисления и результат вычисления корней, а также их расположение на комплексной плоскости (рис. 6). >> numz=[50 125 50]; denz=[1.208 4.404 3.4]; >> sysz=tf(numz, denz); >> sys=feedback(sysz,[0]) Transfer function: 50 s^2 + 125 s + 50 ------------------------- 1.208 s^2 + 4.404 s + 3.4 >> pole(sys) ans = -2.5357 -1.1100 >> pzmap(sys) Построим временные характеристики системы, для чего воспользуемся пакетом MatLab и библиотекой Simulink. Для построения воспользуемся передаточной функцией замкнутой системы (2). На вход 1-го звена подадим входное ступенчатое воздействие с задержкой 1 с, на вход второго – импульсное воздействие с параметрами (Period – 10 sec; Pulse Width – 1 %). В результате путем моделирования замкнутой САУ получим переходную и импульсную переходные характеристики системы. Установившееся значение на выходе системы составило 15 единиц. 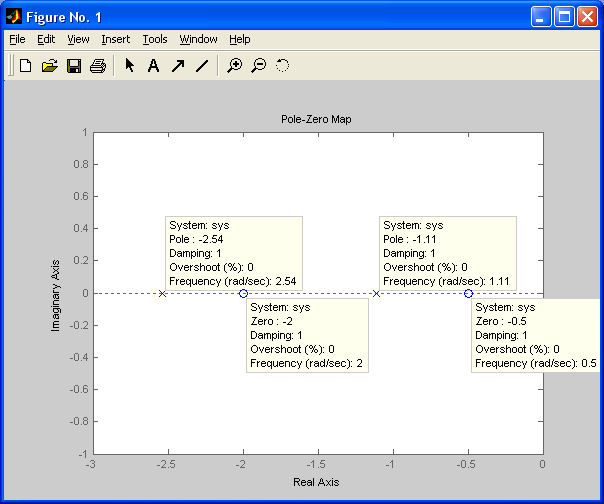 Рисунок 6. Расположение корней характеристического полинома на комплексной плоскости 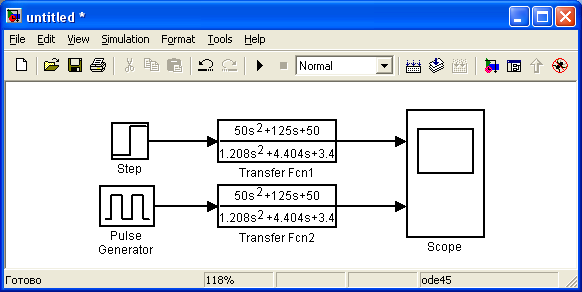 Рисунок 7. Схема для получения временных характеристик 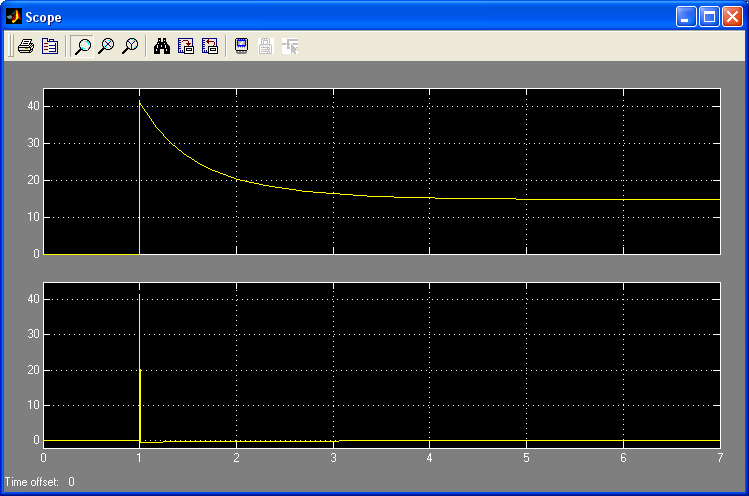 Рисунок7 Схема для получения временных характеристик В завершении работы необходимо: оценить устойчивость системы; сравнить показатели устойчивости системы, полученные с использованием различных критериев устойчивости; сделать вывод о качественных показателях регулирования рассматриваемой системы, о ее работоспособности и целесообразности внедрения её в реальную систему управления. 3. ВАРИАНТЫ РАСЧЕТНЫХ ЗАДАНИЙ 1 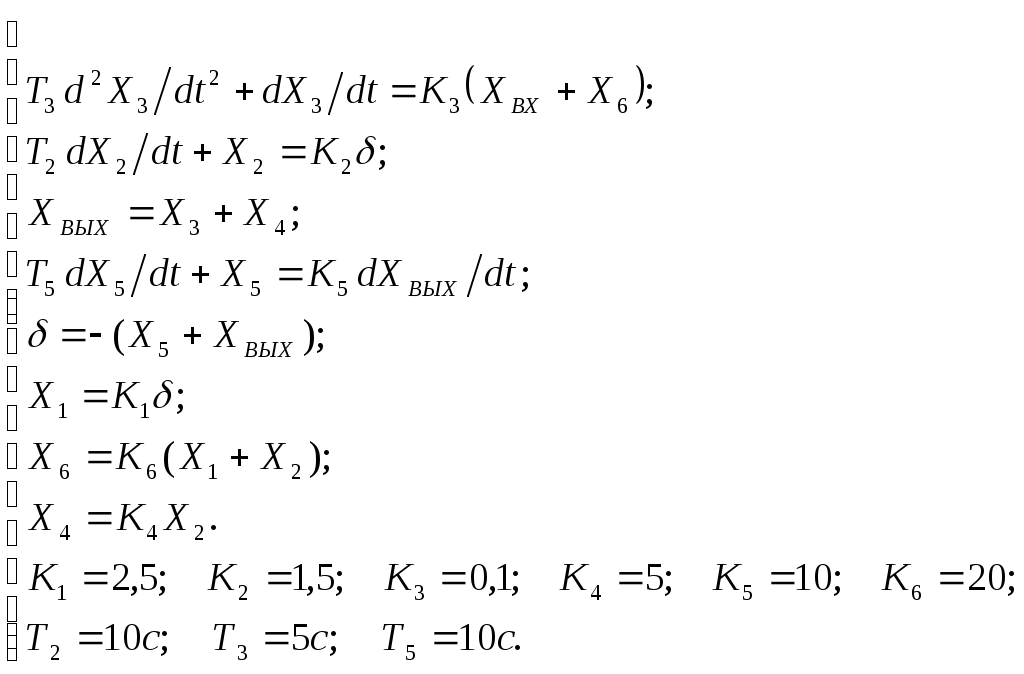 . . 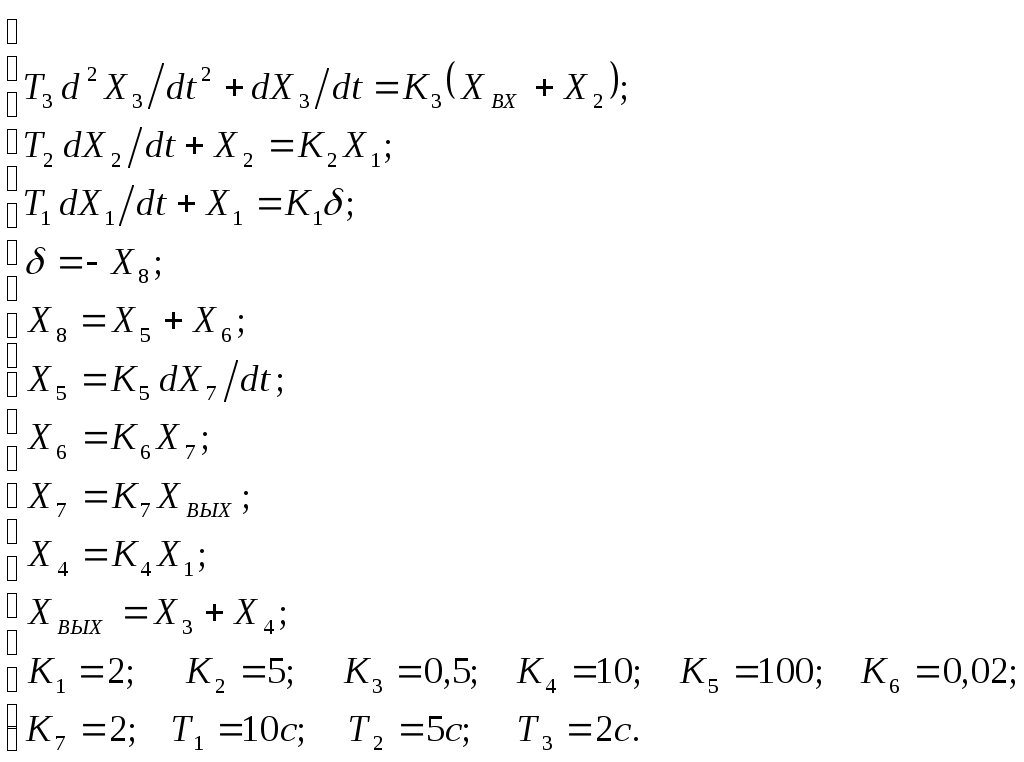 2. 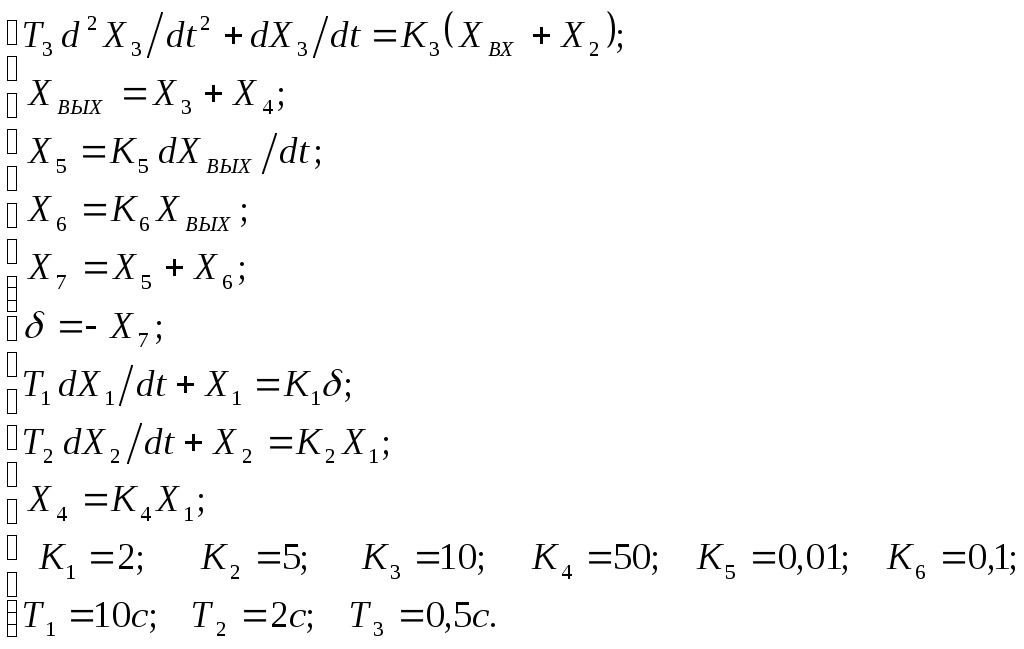 3. 4 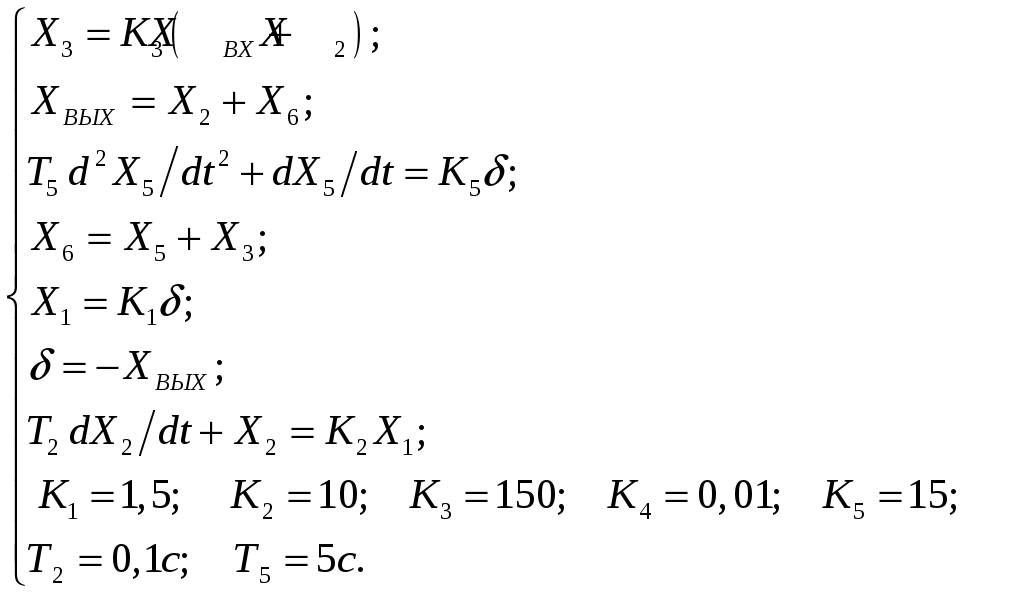 . . 5 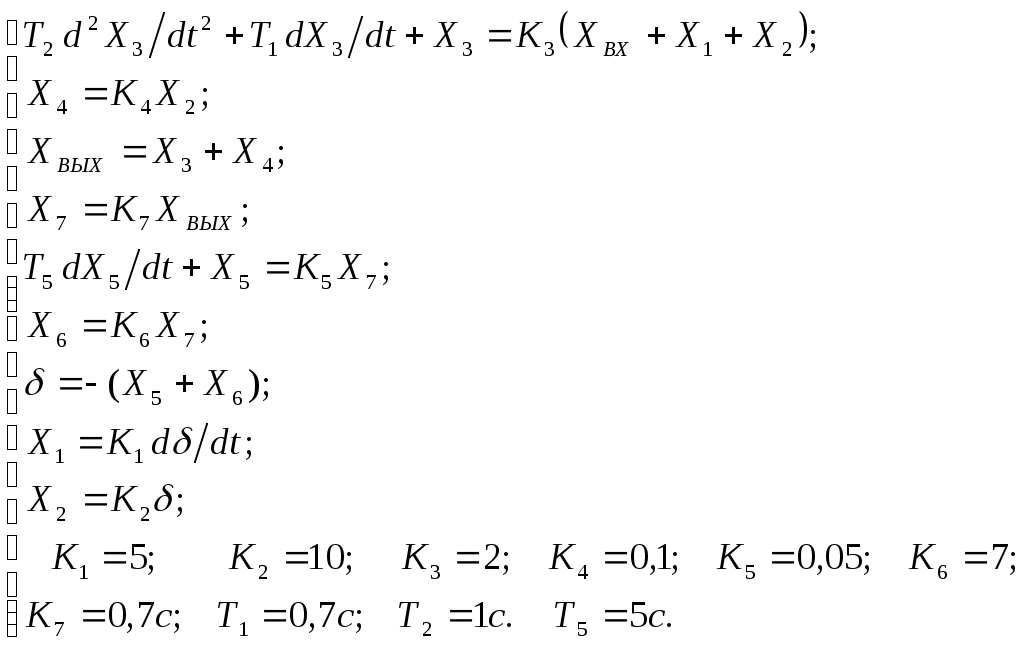 . . 6 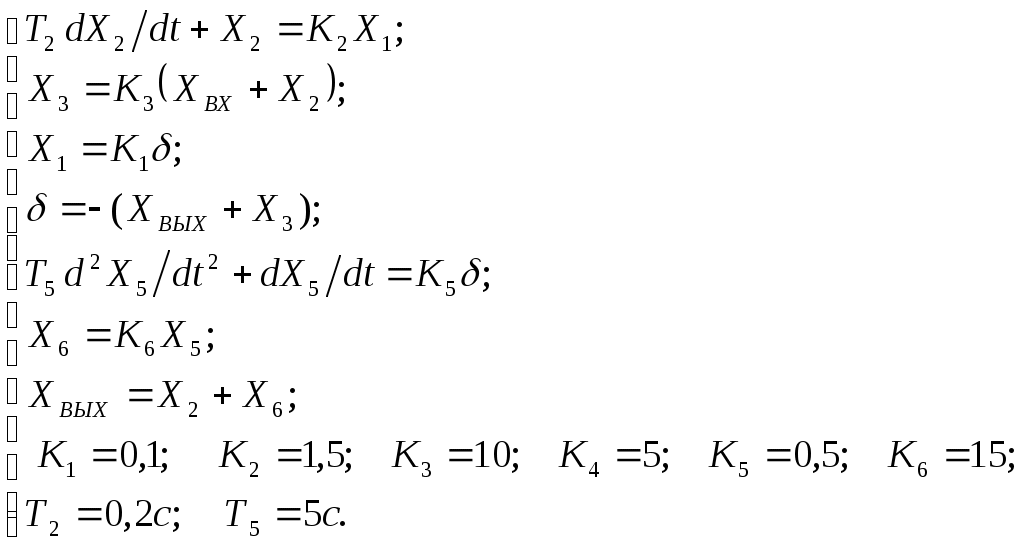 . . 7 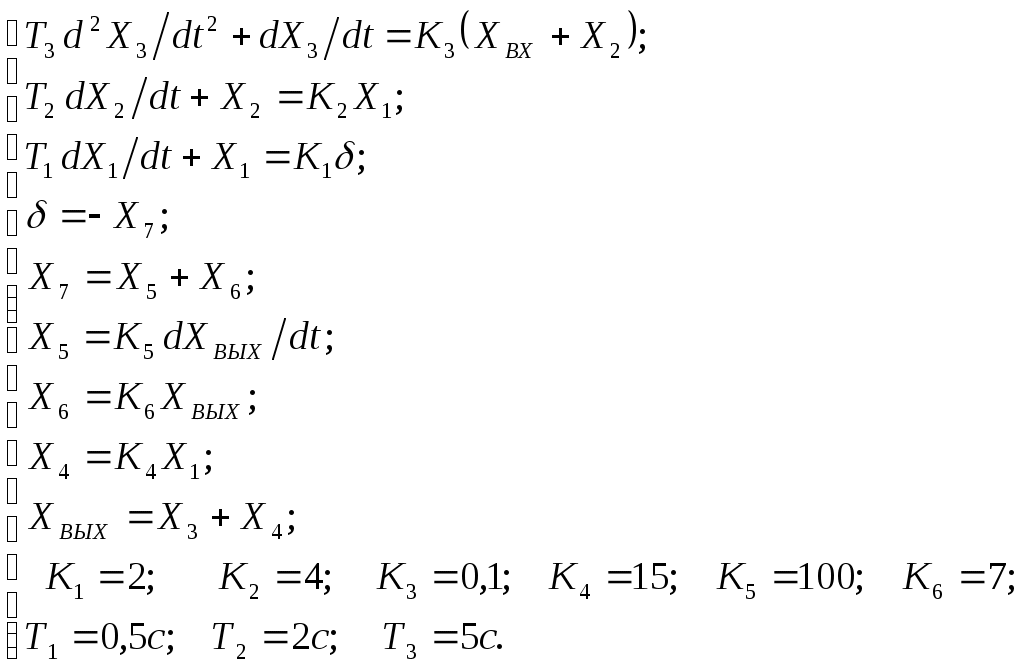 . . 8 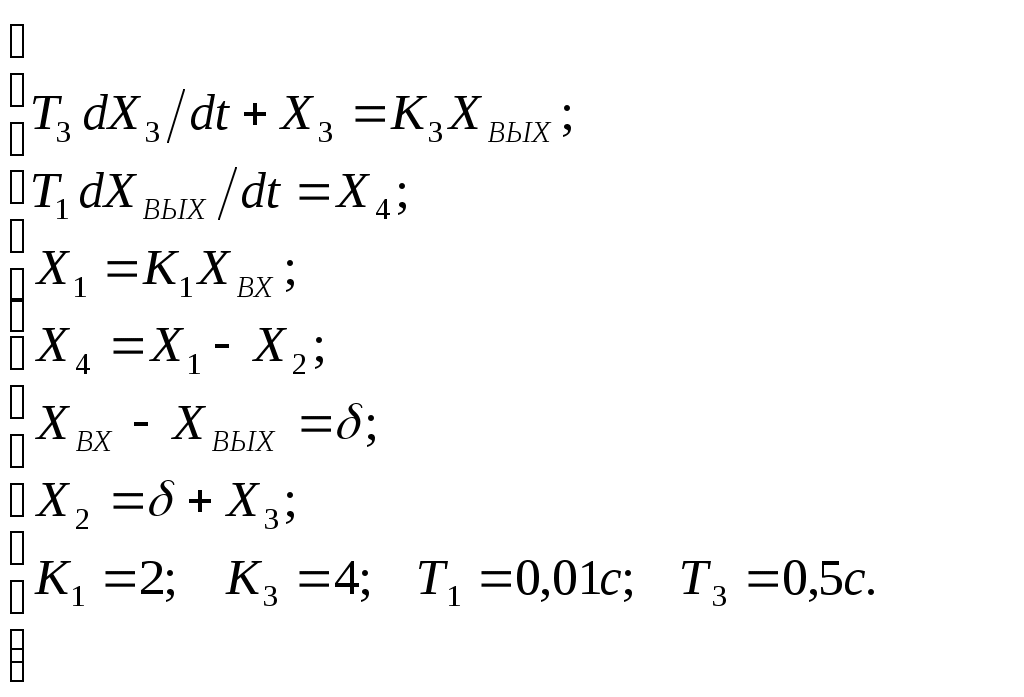 . .9 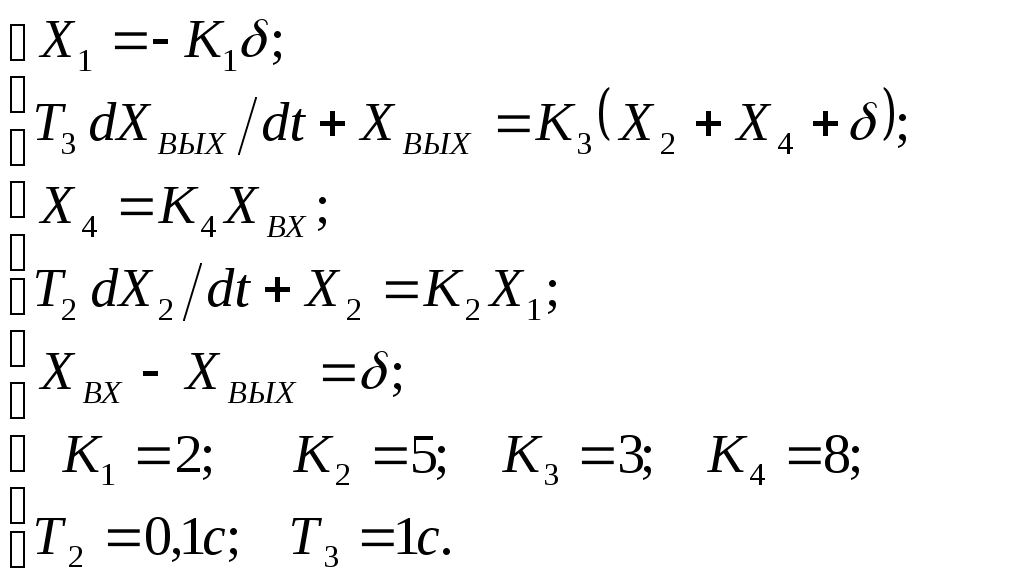 . . 1 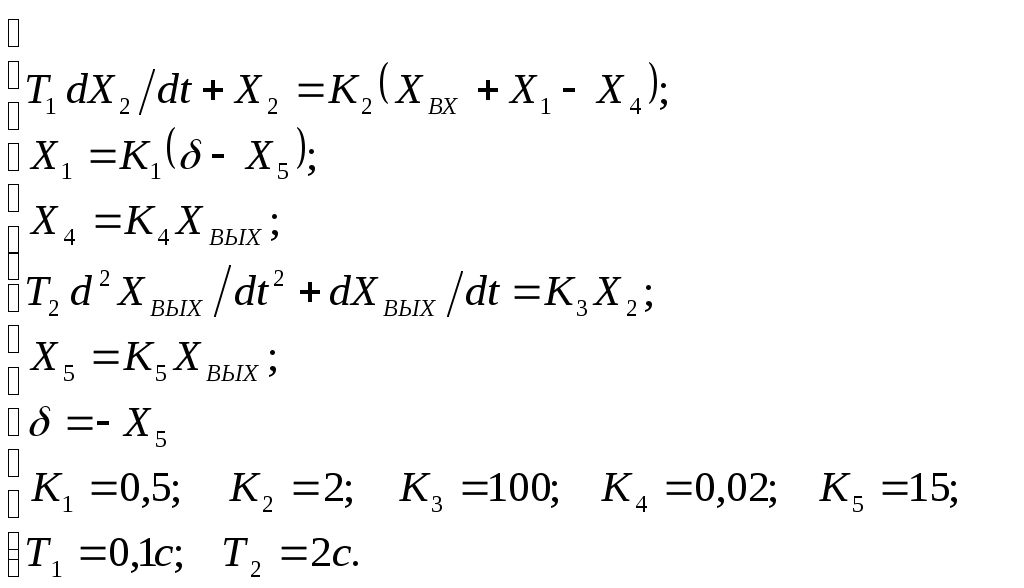 0. 0. 1 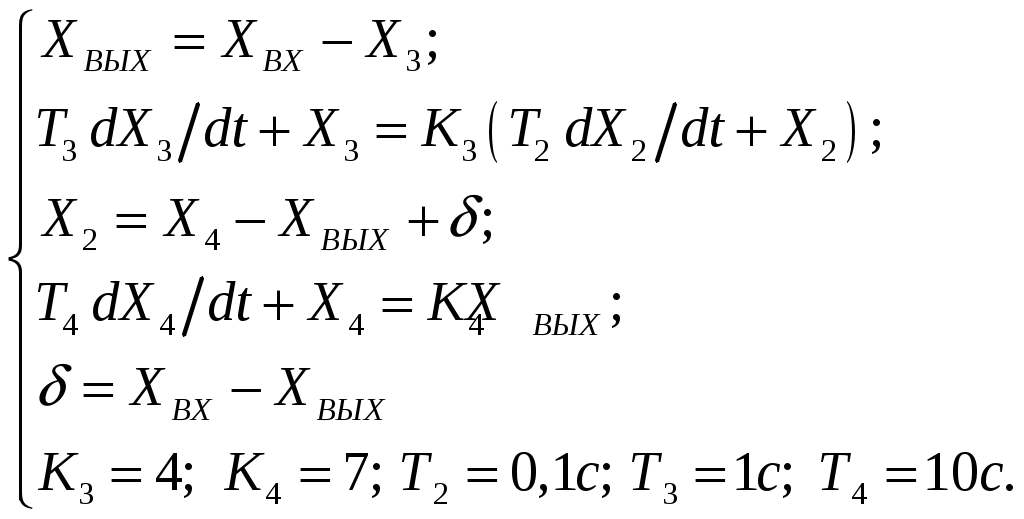 1. 1. 1 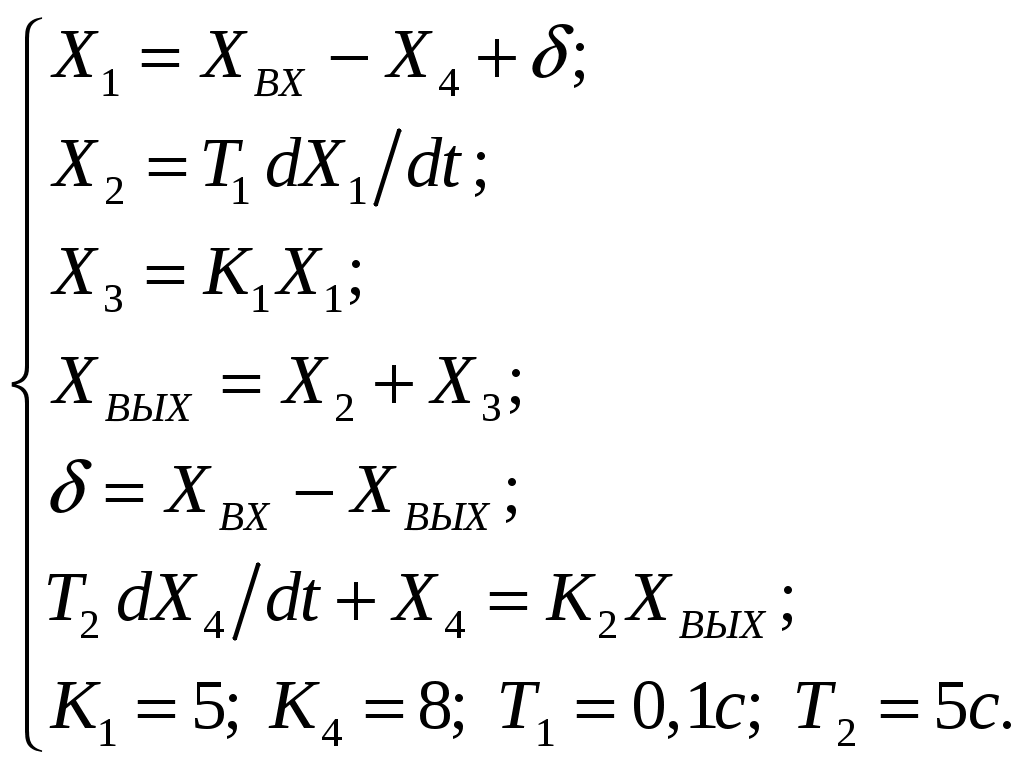 2. 2. 1 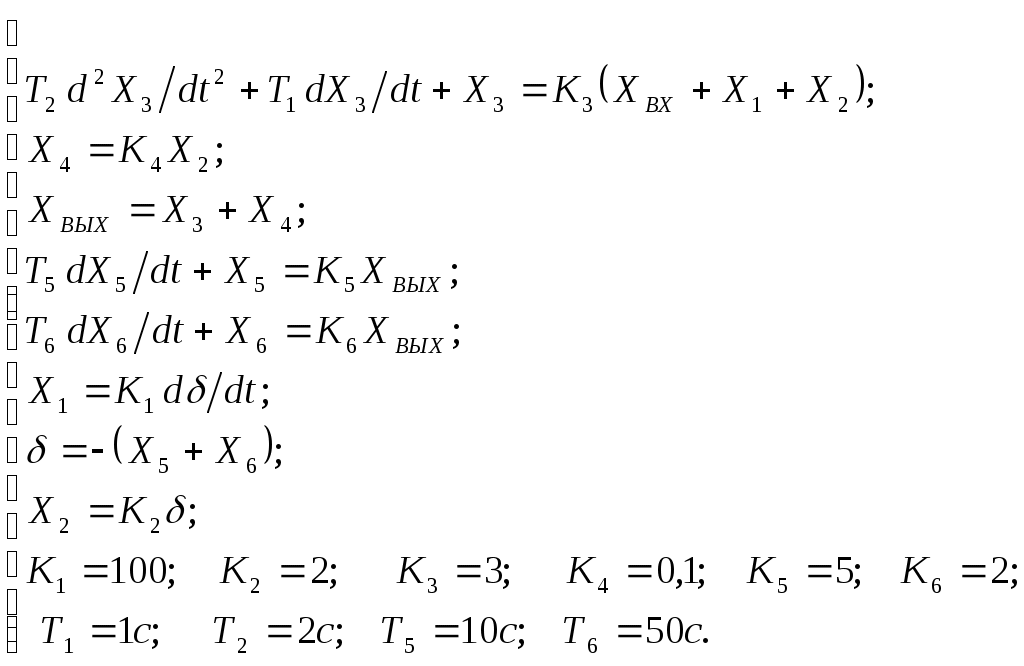 3. 3. 1 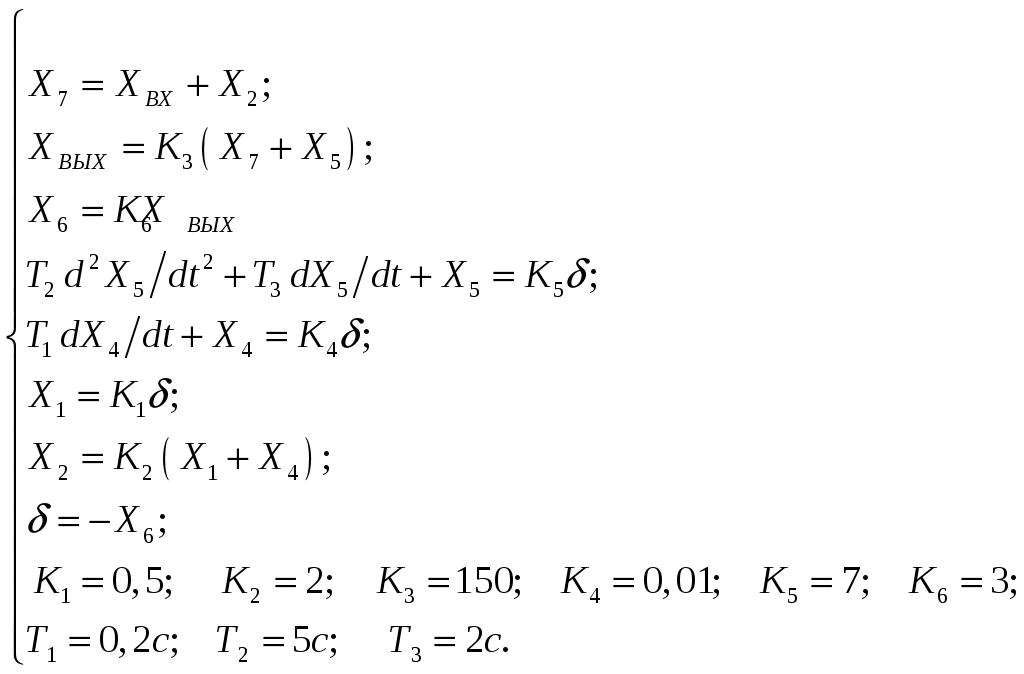 4. 4. 1 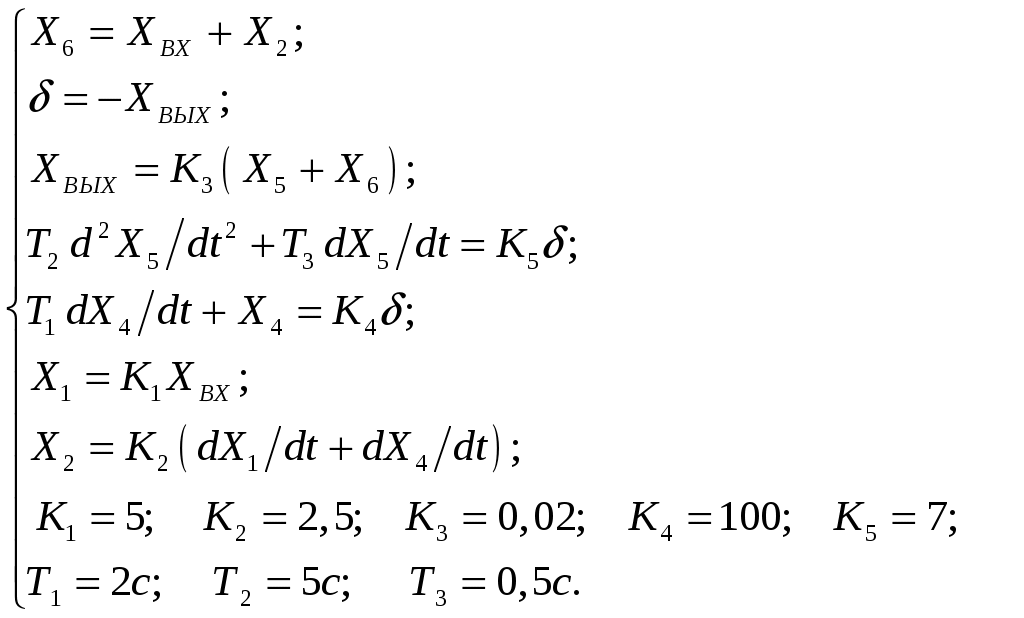 5. 5.1 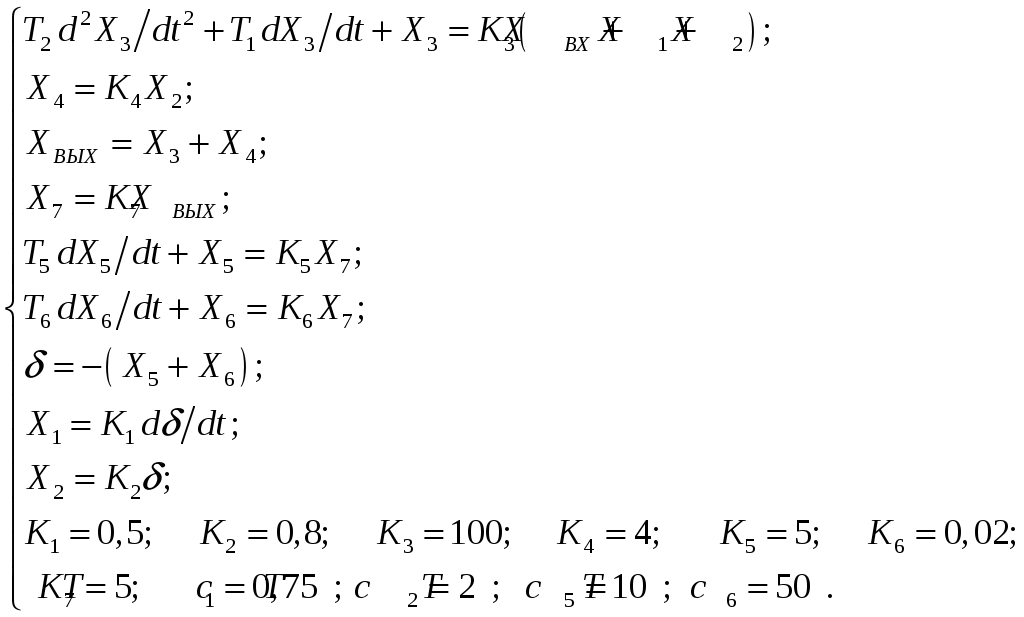 6. 6. 17. 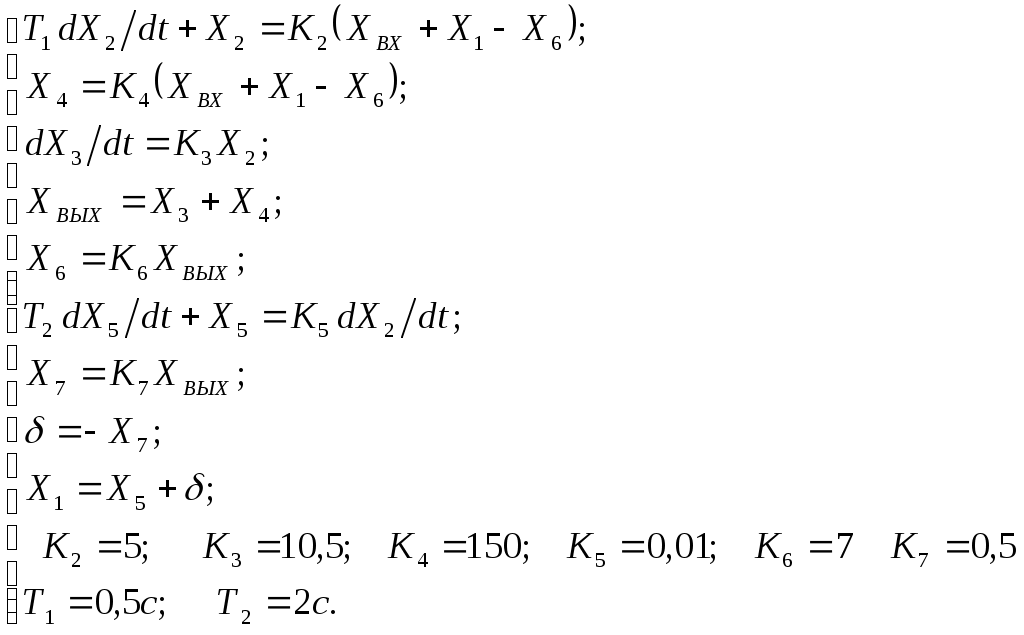 1 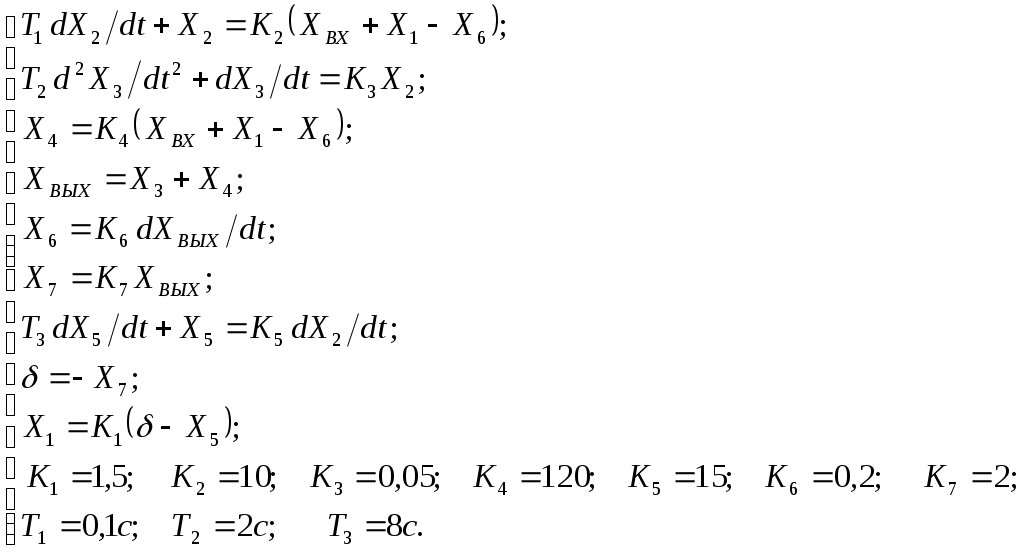 8. 8. 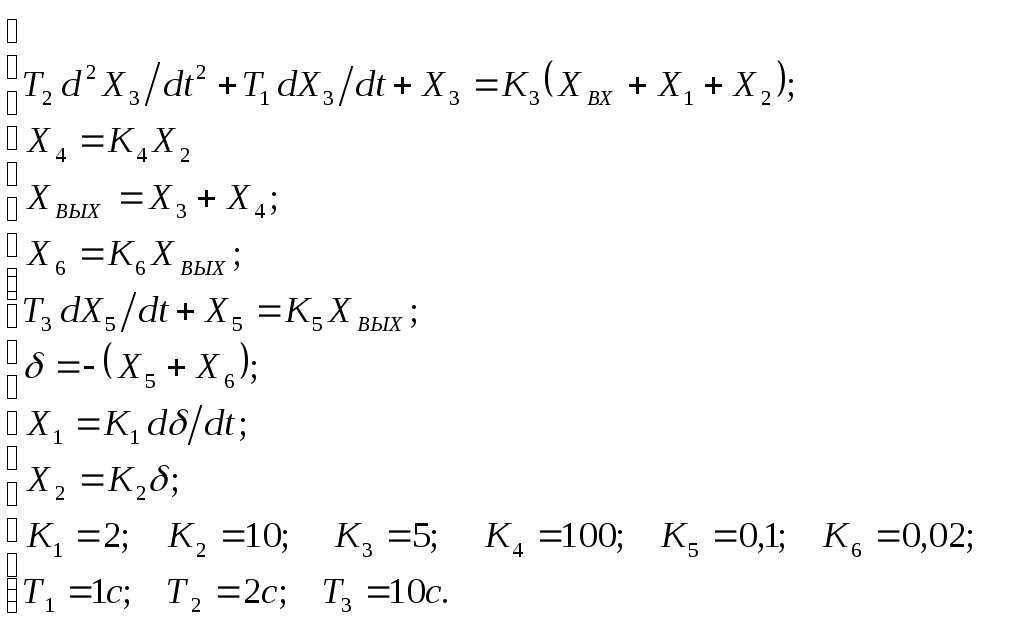 19. 2 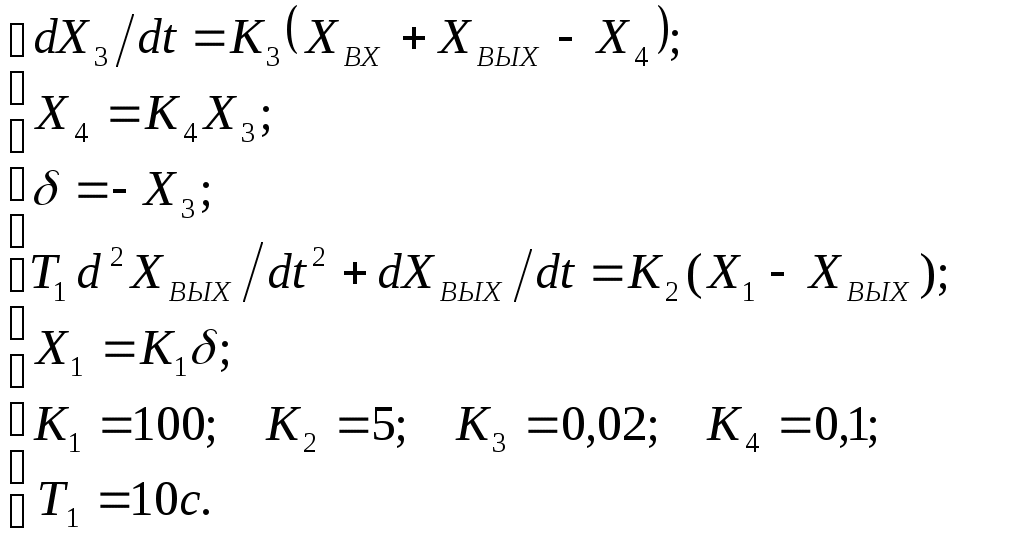 0. 0. 2 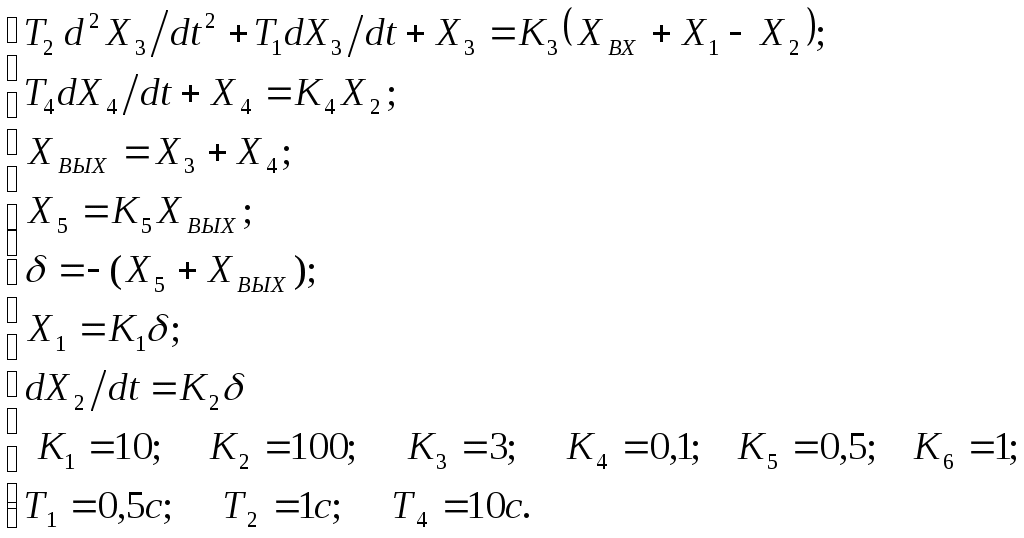 1. 1. 2 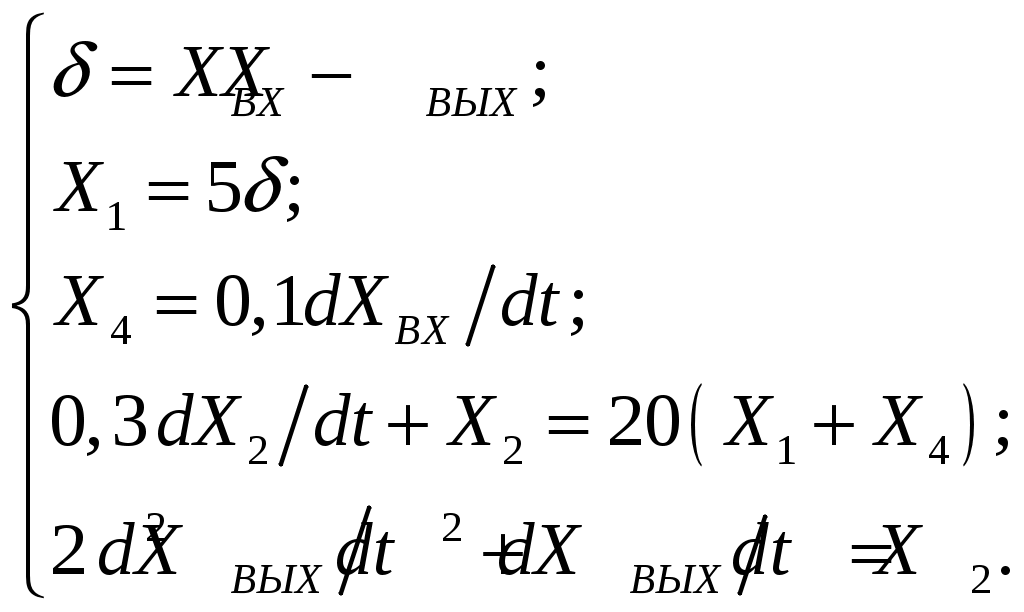 2. 2. 2 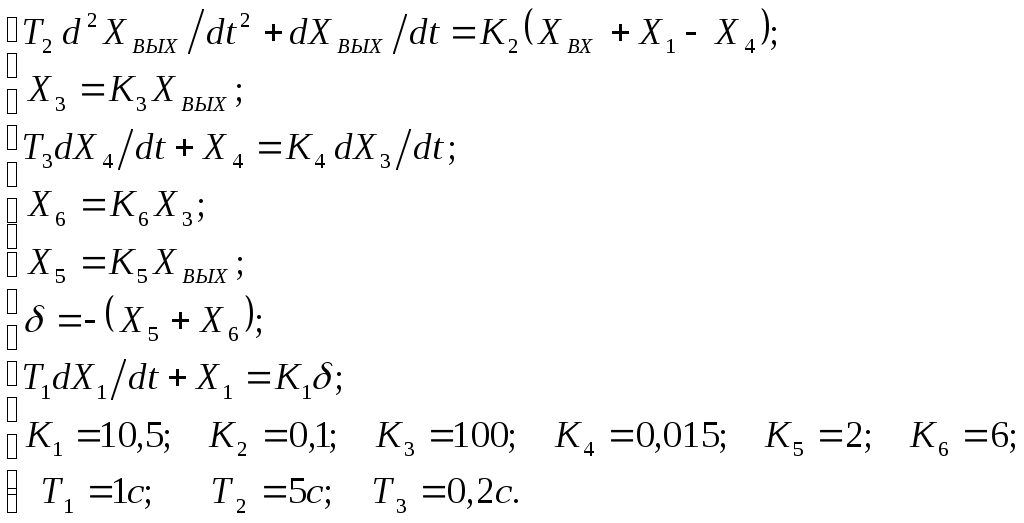 3. 3. 2 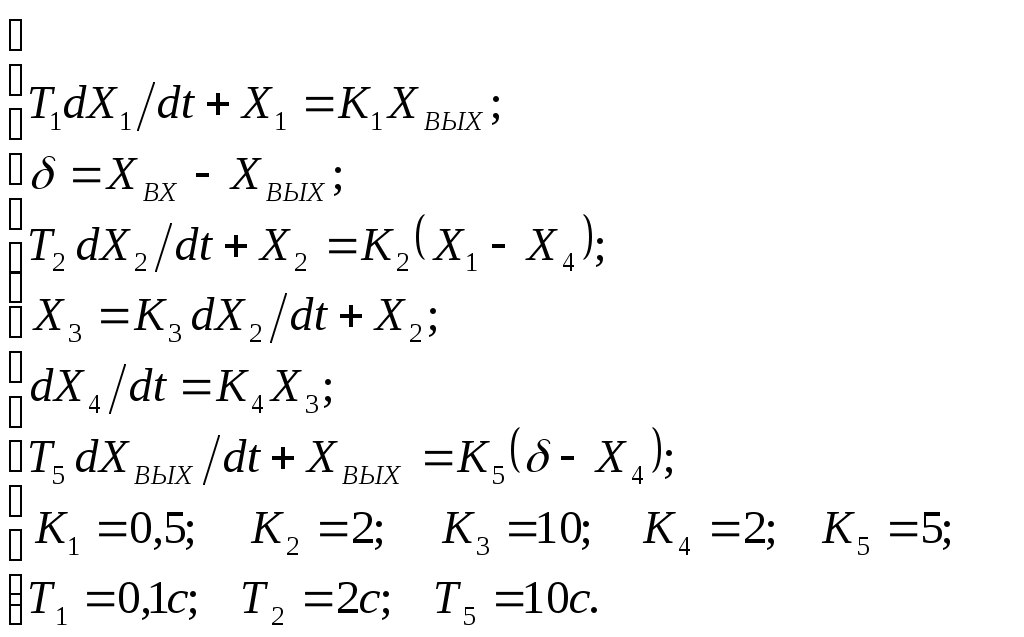 4. 4. 2 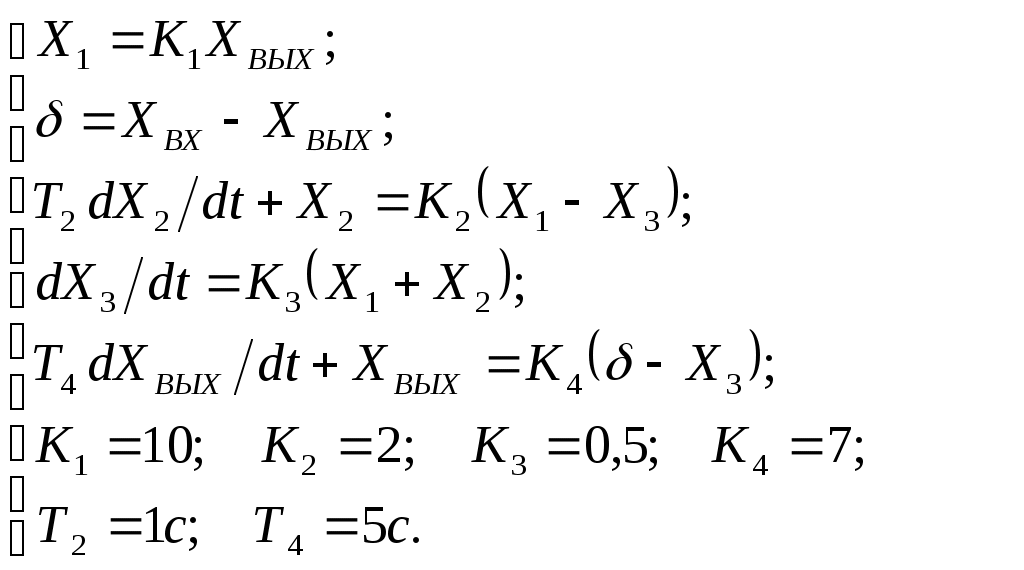 5. 5. 26. 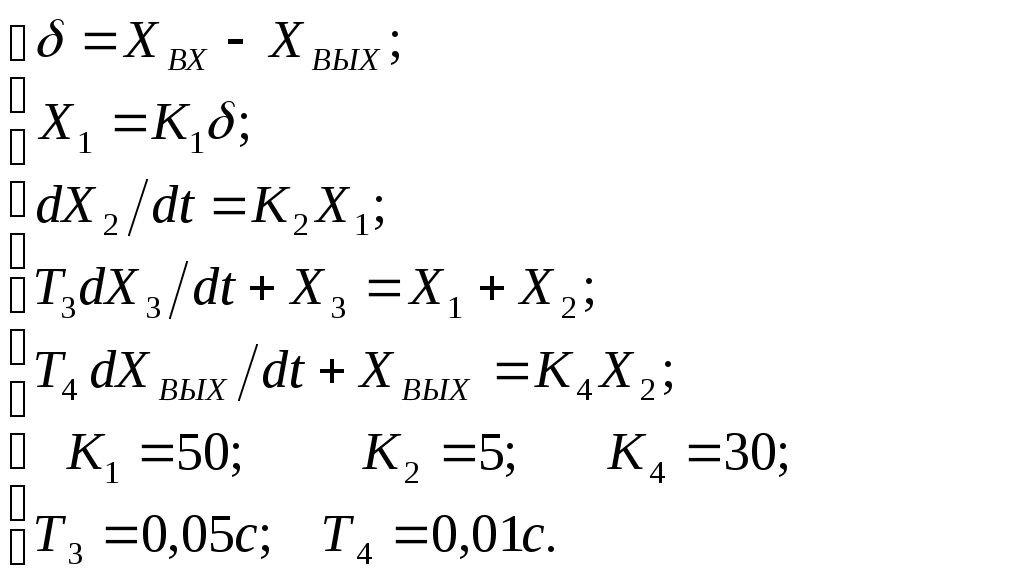 2 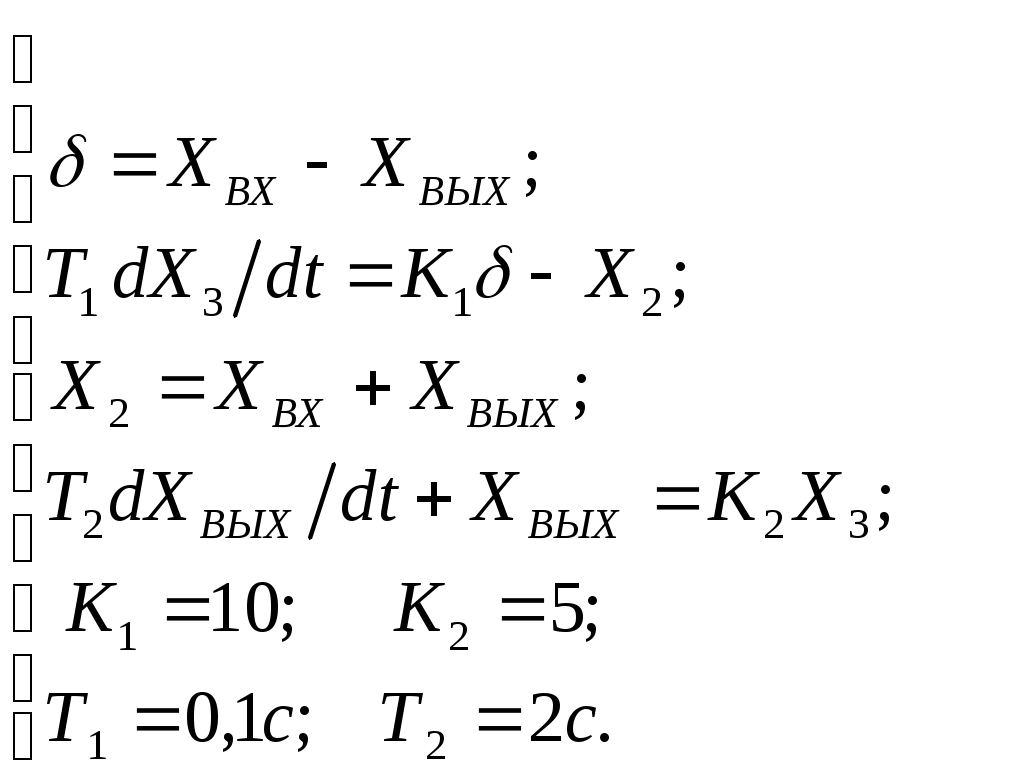 7. 7. 2 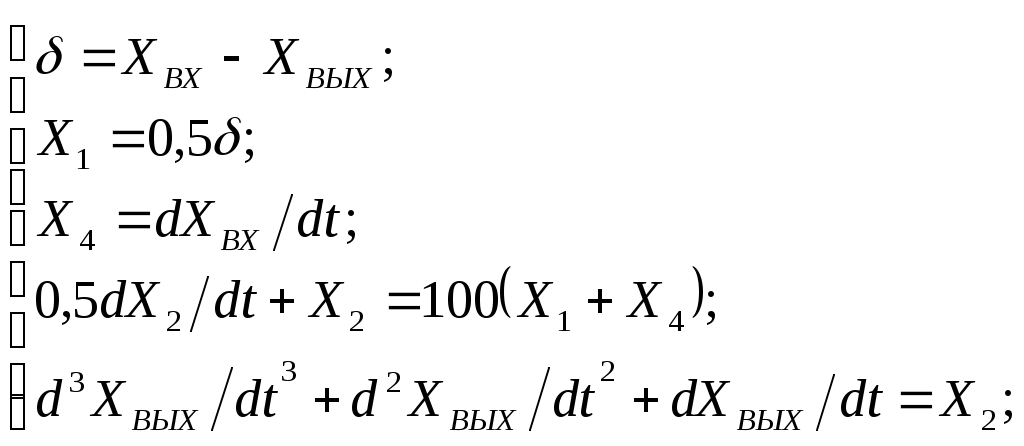 8. 8. 4. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА Теория автоматического управления: учебник для вузов/ под ред. В.Б. Яковлева. – 2-е изд., перераб. – М. : Высшая школа, 2005. – 567 с. Ерофеев А.А. Теория автоматического управления: учебник для вузов / А.А. Ерофеев. - 2-е изд., доп. и перераб. - СПб.: Политехника, 2002. - 302 с. Бесекерский В.А. Сборник задач по теории автоматического регулирования и управления. 5-е изд. перераб. и доп. – М.: Наука, 1987. – 512 с. Солодовников В.В., Плотников В.Н., Яковлев А.В. Основы теории и элементы систем автоматического регулирования. – М.: Машиностроение, 1985. – 195 с. Солодовников В.В., Плотников В.Н., Яковлев А.В. Теория автоматического управления техническими системами. – М.: Изд-во МГТУ, 1993. Топчеев Ю.И. Атлас для проектирования систем автоматического регулирования: Учеб. пособие для вузов. – М.: Машиностроение, 1989. – 752 с.: ил. Фатеев А.В. Расчет автоматических систем. – М.: Высшая школа, 1973. – 336 с. Приложение А. Пример оформления титульного листа Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования Пермский национальный исследовательский политехнический университет Лысьвенский филиал курсовАЯ работа По дисциплине «ТЕОРИЯ автоматического УПРАВЛЕНИЯ» тема: «Расчет системы автоматического управления» Вариант № __ Выполнил студент ________________________________________ И.О. Фамилия подпись, дата Группа АЭП-17-б Направление 13.03.02 «Электроэнергетика и электротехника» Руководитель (должность, ученая степень, звание) ____________ В.Г. Лопатин подпись, дата Лысьва 2017 |
