Мет[1].указ. Новикова В.В. РТА. Мет[1].указ. Новикова В.В. Методические указания по выполнению семестрового домашнего задания по дисциплине Статистика Раздел Общая теория статистики
 Скачать 3.2 Mb. Скачать 3.2 Mb.
|
|
4.4.3. Построение доверительных интервалов Конечной целью моделирования является оценка или прогнозирование показателя Yв зависимости от значений X. Прогноз подразделяется на точечный и интервальный и обычно осуществляется не более чем на одну треть размаха: 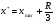 , , где 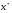 - точка прогноза. - точка прогноза.В точечном прогнозе показателя Yдля 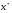 определяется лишь одно число, которое представляет условное среднее и (при выполнении предпосылок регрессионного анализа) наиболее вероятное значение с точки зрения закономерности, отраженной в модели. В таком прогнозе не учитываются отклонения от закономерностей в результате воздействия случайных и неучтенных факторов. определяется лишь одно число, которое представляет условное среднее и (при выполнении предпосылок регрессионного анализа) наиболее вероятное значение с точки зрения закономерности, отраженной в модели. В таком прогнозе не учитываются отклонения от закономерностей в результате воздействия случайных и неучтенных факторов.В интервальном прогнозе отклонения от закономерностей в результате случайных воздействий определяются границами доверительных интервалов. Доверительным интервалом называется такой интервал, которому с заданной степенью вероятности (называемой доверительной) принадлежат истинные значения показателя при условии, что закономерности, отраженные в модели, не противоречат развитию как на участке наблюдения, так и на участке оценки (или в периоде упреждения прогноза). Случайные отклонения от модели проявляются в виде ошибок. Поэтому при определении границ, доверительных интервалов необходимо определить из чего складываются возможные ошибки моделирования, оценки и прогнозирования. При условии, что модель адекватна, и возможные ошибки носят случайный характер, следует различать два основных источника ошибок:
Наличие ошибок первого типа очевидно даже визуально. Величина ошибок аппроксимации характеризуется остаточной дисперсией 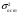 или средней квадратической ошибкой или средней квадратической ошибкой 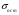 . Распределение этих ошибок для адекватных моделей – нормально (нормальность ошибок – одно из условий адекватности). . Распределение этих ошибок для адекватных моделей – нормально (нормальность ошибок – одно из условий адекватности).Ошибки оценок параметров модели обусловлены тем, что их параметры, фиксированные в модели как однозначные, в действительности являются случайными величинами, так как они оцениваются на основе фактических данных, в которых присутствует как закономерная, так и случайная составляющие. Средние значения этих оценок при выполнении предпосылок регрессионного анализа соответствует истинным значениям параметров, а их дисперсии зависят от остаточной дисперсии, числа наблюдений и вида модели. Общее среднее квадратическое отклонение истинных значений от расчетных может быть представлено как: 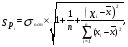 (87) (87) а в точке прогноза: 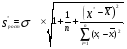 (88) (88) Исходя из предпосылки нормального распределения остатков границы доверительных интервалов определяются по формулам: 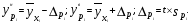 (89) (89)Анализ выражений (88, 89) позволяет для моделей парной регрессии сделать вывод, что доверительные интервалы тем шире, чем: - больше остаточная дисперсия (менее точна модель); - значение 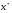 больше удалено от среднего значения больше удалено от среднего значения 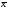 (см. рис. 7.5); (см. рис. 7.5);- сложнее форма модели; - больше заданная доверительная вероятность. Обобщая полученные результаты, можно сделать вывод, что построенная модель обладает хорошим качеством, т.е. она достаточно точна и адекватна исследуемому процессу по всем перечисленным ранее критериям. Учитывая еще и нормальность ряда остатков можно осуществлять точечный и интервальный прогнозы. В связи с этим табл. 7.5 приведены данные для построения доверительных интервалов.  Массив 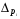 - ширина доверительного интервала; - ширина доверительного интервала; 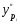 - нижняя граница доверительного интервала; - нижняя граница доверительного интервала; 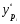 - верхняя граница доверительного интервала вычислены по формулам (87 - 89) с доверительной вероятностью 0,975 и соответствующим ей коэффициентом доверия Стьюдента 2,317. Выбор распределения Стьюдента обусловлен не большим объёмом анализируемой совокупности. - верхняя граница доверительного интервала вычислены по формулам (87 - 89) с доверительной вероятностью 0,975 и соответствующим ей коэффициентом доверия Стьюдента 2,317. Выбор распределения Стьюдента обусловлен не большим объёмом анализируемой совокупности.График доверительных интервалов и график их ширины приведены на рис. 6 и 7. Рис. 6. График доверительных интервалов Рис. 7. График ширины доверительных интервалов С учетом нормального распределения остатков при среднем значении ВТО фирм равном 1067,43 млн. долл. с вероятностью 0,975 прогнозируемые таможенные платежи в бюджет составят от 27,61 до 31,37 млн. долл., при этом условное среднее (наиболее вероятный объём поступлений) ожидается 29,49 млн. долл. ЛИТЕРАТУРА
10. Сигел, Эндрю. Практическая бизнес-статистка: Пер с англ. – М.: Издательский дом «Вильямс», 2004. – 1056 с.: ил. – Парал. Тит. англ. |
