Мет[1].указ. Новикова В.В. РТА. Мет[1].указ. Новикова В.В. Методические указания по выполнению семестрового домашнего задания по дисциплине Статистика Раздел Общая теория статистики
 Скачать 3.2 Mb. Скачать 3.2 Mb.
|
|
2.2. Показатели центра распределения Средняя арифметическая взвешенная: 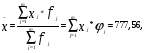 (16) (16) где 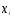 - значения j-ой середины интервалов; - значения j-ой середины интервалов;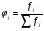 - частости j-го интервала. - частости j-го интервала.Мода и медиана относятся к структурным средним. Их значения находятся из выражений: 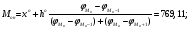 (17) (17)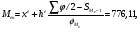 (18) (18)где 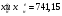 - нижние границы модального и медианного интервалов; - нижние границы модального и медианного интервалов;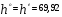 - ширина модального и медианного интервалов; - ширина модального и медианного интервалов;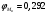 - частость модального интервала; - частость модального интервала;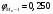 - частость интервала, предшествующего модальному; - частость интервала, предшествующего модальному; - частость интервала следующего за модальным; - частость интервала следующего за модальным;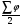 - половина суммы накопленных частостей (равна 0,5); - половина суммы накопленных частостей (равна 0,5);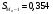 - накопленная частость до медианного интервала; - накопленная частость до медианного интервала;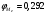 - частость медианного интервала. - частость медианного интервала.2.3. Показатели вариации
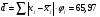 . (19) . (19)3. Дисперсия: 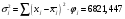 . (20) . (20)4. Среднее квадратическое отклонение:  . (21) . (21)6. Линейный коэффициент вариации: 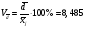 . (23) . (23) 7. Коэффициент вариации: 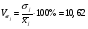 . (24) . (24)8. Относительный показатель квартильной вариации: 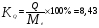 , (25) , (25) где 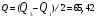 - среднее квартильное расстояние; - среднее квартильное расстояние;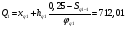 ; (26) ; (26) ; (27) ; (27) - соответственно первая и третья квартили распределения; - соответственно первая и третья квартили распределения;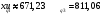 - нижние границы интервалов, в которых находятся первая и третья квартили; - нижние границы интервалов, в которых находятся первая и третья квартили;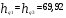 - ширины интервалов первой и третьей квартили; - ширины интервалов первой и третьей квартили;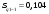 и и 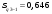 - сумма накопленных частостей в интервалах предшествующих интервалам, в которых находятся первая и третья квартили; - сумма накопленных частостей в интервалах предшествующих интервалам, в которых находятся первая и третья квартили;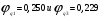 - частости интервалов, в которых находятся первая и третья квартиль. - частости интервалов, в которых находятся первая и третья квартиль.2.4. Показатели дифференциации
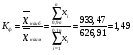 , (28) , (28) где 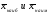 - средние значения для 10% фирм с наибольшими и для 10% с наименьшими значениями ВТО. - средние значения для 10% фирм с наибольшими и для 10% с наименьшими значениями ВТО.
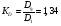 , (29) , (29) где  - максимальное значение у 10% фирм с наименьшими значениями ВТО; - максимальное значение у 10% фирм с наименьшими значениями ВТО; - минимальное значение ВТО у 10% фирм с наибольшими значениями ВТО; - минимальное значение ВТО у 10% фирм с наибольшими значениями ВТО;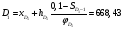 ; (30) ; (30)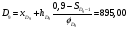 ; (31) ; (31) 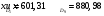 - нижние границы интервалов, в которых находятся первая и девятая децили; - нижние границы интервалов, в которых находятся первая и девятая децили;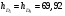 - ширины интервалов первой и девятой децили; - ширины интервалов первой и девятой децили;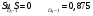 - сумма накопленных частостей в интервалах, предшествующих интервалам, в которых находятся первая и девятая децили; - сумма накопленных частостей в интервалах, предшествующих интервалам, в которых находятся первая и девятая децили;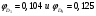 - частости интервалов, в которых находятся первая и девятая децили. - частости интервалов, в которых находятся первая и девятая децили.Следует отметить что оба показателя являются ненормированными. Вследствие этого одно и тоже значение каждого из них можно толковать по-разному. Для устранения указанной неопределенности условимся вычислять значения 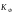 и и 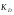 по формулам: по формулам: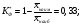 (32) (32) 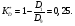 (33) (33)Оценку степени дифференциации можно осуществить по шкале Чеддока. В соответствии со шкалой Чеддока степень дифференциации фирм по ВТО является слабой. Шкала Чеддока Таблица 3
В статистике для изучения степени неравномерности распределения определенного суммарного показателя между единицами отдельных групп вариационного ряда используется кривая Лоренца (или кривая концентрации). Для ее построения распределение единиц совокупности (числа банков) и распределение суммарного показателя (суммы прибыли в банках) должны быть представлены в долях или процентах, а затем для обоих распределений рассчитываются накопленные (кумулятивные) итоги.
Рассчитывается на основе кривой Лоренца 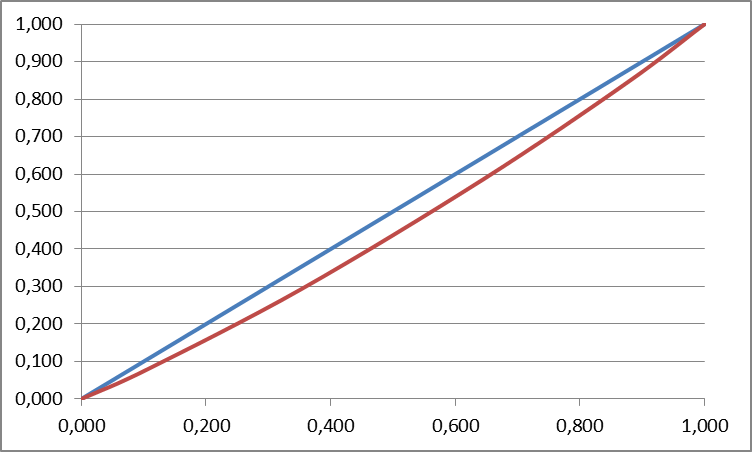 Рис. Кривая Лоренца 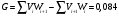 , (34) , (34)где 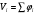 , , 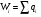 . .При построении графика на горизонтальной линии нанесена шкала для ряда накопленных частостей, а на вертикальной линии — шкала для накопленных относительных величин размера изучаемого признака (графы 5 и 7 табл.2 соответственно). 2.6. Показатели формы распределения Показатель асимметрии для сгруппированных данных находится из выражения  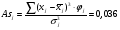 , (35) , (35)а показатель эксцесса: 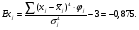 (36) (36)2.7. Проверка соответствия эмпирического распределения внешнеторгового оборота фирм нормальному распределению с помощью критериев согласия Пирсона, Романовского и Колмогорова Критерий Пирсона 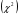 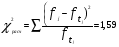 (37) (37)где 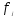 — эмпирические частоты (частости) в интервале; — эмпирические частоты (частости) в интервале; — теоретические частоты (частости) в интервале. — теоретические частоты (частости) в интервале.Значения теоретических частот (графа 9 табл. 2) рассчитаны с помощью функции плотности нормального распределения ОКРУГЛ(n*h*НОРМ.РАСП(X, Среднее, Стандартное – откл, Интегральный);0), где n=48 – объём выборки; h=69,92 – ширина интервала; X – средние значения ВТО в интервалах, (графа 2 табл. 2); Среднее = 72,29; Стандартное_ откл = 82,592; Интегральный = 0 - логическое значение, определяющее форму функции (ноль соответствует плотности распределения); 0 – количество знаков после запятой в функции округления. Расчётное значение критерия сравнивается с критическим 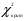 , которое определено с помощью функции ХИ2ОБР ПХ(0,05; 2) EXCEL, где 0,05 - уровень значимости, а 2 - количество степеней свободы (Ксс) для данного примера, определяемое из выражения Ксс=m-Кp-1. Здесь Кр – количество параметров в законе распределения случайной величины. Для нормального закона распределения Кр=2 ( , которое определено с помощью функции ХИ2ОБР ПХ(0,05; 2) EXCEL, где 0,05 - уровень значимости, а 2 - количество степеней свободы (Ксс) для данного примера, определяемое из выражения Ксс=m-Кp-1. Здесь Кр – количество параметров в законе распределения случайной величины. Для нормального закона распределения Кр=2 (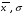 ). Формула = ХИ2ОБР ПХ(0,05; 2) рассчитывает значение 5,99, задающее правостороннюю критическую область (5,99; +∞). Так как выполняется условие ). Формула = ХИ2ОБР ПХ(0,05; 2) рассчитывает значение 5,99, задающее правостороннюю критическую область (5,99; +∞). Так как выполняется условие 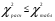 , то отклонения теоретических частот от эмпирических являются случайными и распределение ВТО фирм не противоречит нормальному. , то отклонения теоретических частот от эмпирических являются случайными и распределение ВТО фирм не противоречит нормальному.Критерий Романовского 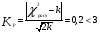 , (38) где , (38) где 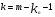 - число степеней свободы; - число степеней свободы;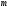 — число групп; — число групп;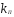 —количество параметров в теоретическом законе распределения (для нормального закона распределения —количество параметров в теоретическом законе распределения (для нормального закона распределения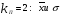 ); );В данном примере расчётное значение меньше 3, следовательно можно принять гипотезу о нормальном характере эмпирического распределения. Критерий Колмогорова ( 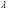 ) )Основан на определении максимального (по модулю) расхождения между накопленными частотами эмпирического и теоретического распределений (d) ,графа 11 табл. 2: 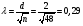 . (39) . (39)По известному значению 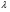 определяется вероятность определяется вероятность 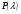 (П.2 табл. 1), если она близка к 1, то расхождение между частотами случайны. (П.2 табл. 1), если она близка к 1, то расхождение между частотами случайны.График эмпирических и теоретических частот приведен на рис. 3. Рис.3 График эмпирических и теоретических частот Анализ результатов расчета позволяет сделать следующие выводы:
3. Определение доверительного интервала для средней величины внешнеторгового оборота фирм в генеральной совокупности Величина доверительного интервала (предельная ошибка выборки) находится из выражения 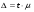 , (40) , (40)где t – коэффициент доверия; 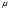 - средняя ошибка выборки. - средняя ошибка выборки.Средняя ошибка бесповторной выборки:  , (41) , (41)где 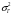 - дисперсия генеральной совокупности; - дисперсия генеральной совокупности;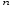 - объем выборочной совокупности; - объем выборочной совокупности;N – объём генеральной совокупности. В случае малой выборки (n<100) средняя ошибка бесповторной выборки находится из выражения: 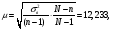 (42) (42)где 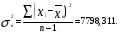 Коэффициент доверия в распределении Стьюдента является функцией доверительной вероятности и функцией объема выборки. Его значение получим с помощью функции СТЬЮДЕНТ.ОБР.2Х (0,05; 47), где 0,05 – уровень значимости, n-1=47- количество степеней свободы. 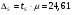 . .Выборка считается репрезентативной, если величина ее относительной ошибки составляет не более 5%, т.е. 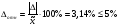 (43) (43)Учитывая, что 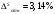 , выборку следует признать представительной. , выборку следует признать представительной. 4. Анализ зависимости таможенных платежей от внешнеторгового оборота фирм 4.1 Построение групповой таблицы. Для построения групповой таблицы вычисляются средние значения результативного признака в каждой группе фирм (графа 6 табл. 5.2). Сравнив их значения, можно предположить о наличии прямой корреляционной зависимости между признаками, что иллюстрируется рис. 4. Рис. 4. Зависимость средних перечислений в бюджет от среднего значения ВТО фирм 4.2. Проверка правила сложения дисперсий и оценка степени влияния факторного признака на величину результативного. Правило сложения дисперсий заключается в равенстве общей дисперсии сумме средней из внутригрупповых и межгрупповой дисперсий, т.е.: 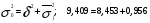 , (44) , (44)где 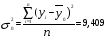 , (45) , (45)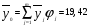 — общая средняя арифметическая результативного признака; — общая средняя арифметическая результативного признака;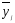 _ среднее значение результативного признака в _ среднее значение результативного признака в 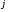 - ой группе; - ой группе; 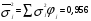 - cредняя из внутригрупповых дисперсий; - cредняя из внутригрупповых дисперсий; 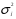 —дисперсия в j-ой группе (графа 13 табл. 5.2), вычисляемая по формуле: —дисперсия в j-ой группе (графа 13 табл. 5.2), вычисляемая по формуле: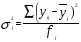 ; ; 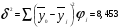 - межгрупповая дисперсия; - межгрупповая дисперсия;Как следует из выражения (44) правило сложения дисперсий выполняется. Разделив левую и правую части выражения (44) на общую дисперсию получим следующее тождество: 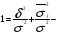 доли средней из внутригрупповых и межгрупповой дисперсий в сумме равны единице. доли средней из внутригрупповых и межгрупповой дисперсий в сумме равны единице. Второе слагаемое именуется эмпирическим коэффициентом детерминации (причинности) и обозначается 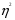 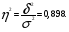 (46) (46)Квадратный корень из коэффициента детерминации принято называть корреляционным отношением: 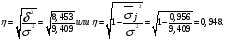 (47) (47)Изменяется корреляционное отношение от 0 до 1. При недостаточном количестве данных в выделенных группах к рассчитанной величине корреляционного отношения вносится поправка:  , (48) где m — число выделенных групп. , (48) где m — число выделенных групп.Для оценки значимости корреляционного отношения можно применить однофакторный дисперсионный анализ. Его логика рассуждений сводится к следующему: Пусть 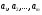 - математическое ожидание результативного признака, соответственно в группах - математическое ожидание результативного признака, соответственно в группах 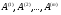 . Если при изменении уровня фактора групповые математические ожидания не изменяются, то результативный признак не зависит от фактора А - в противном случае такая зависимость имеется. . Если при изменении уровня фактора групповые математические ожидания не изменяются, то результативный признак не зависит от фактора А - в противном случае такая зависимость имеется.В связи с тем, что числовые значения математических ожиданий неизвестны, то возникает задача проверки гипотезы 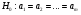 Проверить данную гипотезу можно при соблюдении следующих требований при каждом значении уровня фактора: 1. наблюдения независимы и проводятся в одинаковых условиях; 2. результативный признак имеет нормальный закон распределения с постоянной для различных уровней генеральной дисперсией. Для ответа на второй вопрос вычислим значения относительных показателей асимметрии и эксцесса  для зависимой переменной. Учитывая, что каждый из них меньше 1,5 эмпирическое распределение таможенных платежей в бюджет не противоречит нормальному. для зависимой переменной. Учитывая, что каждый из них меньше 1,5 эмпирическое распределение таможенных платежей в бюджет не противоречит нормальному. Проверим выполнение гипотезы: 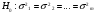 (49) (49)с помощью критерия Бартлетта: 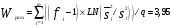 где 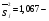 остаточная дисперсия, что является синонимом средней из внутригрупповых выборочных дисперсий; остаточная дисперсия, что является синонимом средней из внутригрупповых выборочных дисперсий;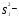 выборочная дисперсия в выборочная дисперсия в 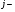 ой группе (графа 14 табл. 5.2); ой группе (графа 14 табл. 5.2); 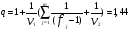 ; ;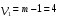 ; ;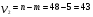 . . При выполнении гипотезы о равенстве дисперсий, величина w имеет распределение близкое к 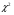 с с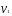 степенями свободы. степенями свободы.При соблюдении условия 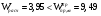 гипотеза (7.14) подтверждается. гипотеза (7.14) подтверждается. Здесь 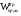 - правосторонняя критическая точка при заданном уровне значимости - правосторонняя критическая точка при заданном уровне значимости 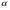 , определяющая критический интервал ( , определяющая критический интервал (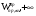 ). ).Далее можно приступить к проверке гипотезы 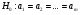 . Для этого сформируем массив значений результативного признака по группам (табл. 4). . Для этого сформируем массив значений результативного признака по группам (табл. 4).Массив значений результативного признака Таблица 4  Обратимся к режиму работы «Однофакторный дисперсионный анализ».
Проверка гипотезы о равенстве математических ожиданий основывается на сравнении оценок факторной 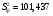 и остаточной и остаточной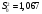 дисперсий. В математической статистике доказывается, что если гипотеза о равенстве математических ожиданий подтверждается, то величина дисперсий. В математической статистике доказывается, что если гипотеза о равенстве математических ожиданий подтверждается, то величина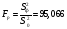 имеет F – распределения с числом свободы имеет F – распределения с числом свободы 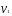 и и 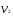 , т.е. , т.е.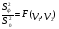 , где , где 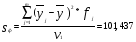 ; ; 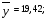 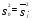 При использовании F – критерия строится правосторонняя область ( 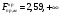 ), т.к. обычно ), т.к. обычно 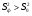 . Если расчетное значение F – критерия . Если расчетное значение F – критерия 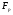 попадает в указанный интервал, то гипотеза о равенстве групповых математических ожиданий отвергается, т.е. считаем, что фактор А влияет на результативный признак Y и можно измерить степень этого влияния с помощью корреляционного отношения. попадает в указанный интервал, то гипотеза о равенстве групповых математических ожиданий отвергается, т.е. считаем, что фактор А влияет на результативный признак Y и можно измерить степень этого влияния с помощью корреляционного отношения. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||