Мет[1].указ. Новикова В.В. РТА. Мет[1].указ. Новикова В.В. Методические указания по выполнению семестрового домашнего задания по дисциплине Статистика Раздел Общая теория статистики
 Скачать 3.2 Mb.
|
|
Раздел «Общая теория статистики» Государственное казенное образовательное учреждение высшего профессионального образования РОССИЙСКАЯ ТАМОЖЕННАЯ АКАДЕМИЯ Кафедра таможенной статистики Домашнее задание по дисциплине «Статистика» Раздел «Общая теория статистики» Вариант № 37__
Москва – 2013 Семестровое домашнее задание по дисциплине «Статистика» Раздел «Общая теория статистики» 1. Проверка первичной информации на однородность, наличие аномальных наблюдений и нормальность распределения 32 2. Вариационный ряд распределения активов банков и система показателей, вычисляемая на его основе 36 2.1. Определение количества групп 36 2.2. Показатели центра распределения 41 2.3. Показатели вариации 42 2.4. Показатели дифференциации 43 2.5. Показатели концентрации 44 2.6. Показатели формы распределения 45 2.7. Проверка соответствия эмпирического распределения внешнеторгового оборота фирм нормальному распределению с помощью критериев согласия Пирсона, Романовского и Колмогорова 45 3. Определение доверительного интервала для средней величины внешнеторгового оборота фирм в генеральной совокупности 47 4. Анализ зависимости таможенных платежей в бюджет от внешнеторгового оборота фирм 48 4.1. Построение групповой таблицы 48 4.2. Проверка правила сложения дисперсий и оценка степени влияния факторного признака на величину результативного 49 4.3. Оценка степени взаимной согласованности между суммой внешнеторгового оборота фирм и величиной таможенных платежей в бюджет с помощью линейного коэффициента корреляции, проверка его значимости и возможности использования линейной функции в качестве формы уравнения 53 4.4. Построение уравнения парной регрессии 55 4.4.1. Статистический анализ модели 58 4.4.2. Оценка качества построенной модели 58 4.4.3. Построение доверительных интервалов 67 Литература 73 1. Проверка первичной информации на однородность, наличие аномальных наблюдений и нормальность распределения Исходные данные приведены в табл. 1
Совокупность считается однородной, если коэффициент ее вариации меньше 33%.  , (1) где  - среднее значение; (2) - среднее квадратическое отклонение; (3) n – объем совокупности. Если исходные данные являются эмпирическими, то их необходимо проверить на наличие аномальных наблюдений (резко выделяющихся единиц совокупности):  или  , (4) . (5)Если условия (4) или (5) не выполняются, то соответствующие единицы совокупности исключаются из дальнейшего рассмотрения, а значения  пересчитываются.Гипотеза о нормальном распределении активов банков принимается, если выполняются оба соотношения:  , (6)где  - относительный показатель ассиметрии; (7) - показатель ассиметрии; (8) -средняя квадратическая ошибка асимметрии; (9) - относительный показатель эксцесса; (10) - показатель эксцесса; (11) - средняя квадратическая ошибка эксцесса. (12) Анализ результатов расчета позволяет сделать следующие выводы:
2. Вариационный ряд распределения активов банков и система показателей, вычисляемая на его основе 2.1. Определение количества групп Количество групп (интервалов) вариационного ряда можно вычислить по формуле Стерджесса:  . (13) Полученное значение округляют до ближайшего целого меньшего. Кроме того, желательно чтобы эмпирическое распределение было одномодальным, а частота каждого из интервалов была не меньше двух. С учётом изложенного, количество интервалов (m) для рассматриваемого примера выбрано равным 5. Ширина интервала рассчитывается по формуле: , (14)где  - размах вариации. (15)Значения частот в группах можно определить с помощью подпрограммы "Гистограмма" пакета “Анализ данных” EXCEL. Для выполнения дальнейших расчетов, полученные результаты (интервалы и частоты) перепишем в табл. 2. Группировка фирм по объёму внешнеторгового оборота Таблица 2  где 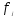 - частота (число фирм) в интервале  ; - среднее значение ВТО в интервале ; - частость (доля фирм) в интервале ; - суммарные таможенные платежи в бюджет в - ой группе фирм, млн. долл.; - частость (доля) платежей в интервале .В каждой выделенной группе различают нижнюю и верхнюю границы интервала. Так, в последней группе фирм по объёму ВТО нижняя граница — 880,98, а верхняя — 950,90 млн. долл. Ряд распределения, состоящий из двух граф (варианты и частоты), иногда дополняется другими графами, необходимыми для вычисления отдельных статистических показателей или для более отчетливого выражения характера вариации изучаемого признака. Достаточно часто в ряд вводится графа, в которой подсчитываются накопленные частоты  Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем данное значение, и исчисляются путем последовательного прибавления к частоте первого интервала частот последующих интервалов. Частоты ряда (  ) могут быть заменены частостями ( ), которые представляют собой частоты, выраженные в относительных числах (долях или процентах) и рассчитанные путем деления частоты каждого интервала на их общую сумму.Диаграмма частот ряда распределения приведена на рис. 1. Рис.1 Диаграмма частот ряда распределения |
), следовательно, средняя величина является обобщающей характеристикой ВТО фирм и отражает типичный уровень в расчете на одну фирму в конкретных условиях места и времени.