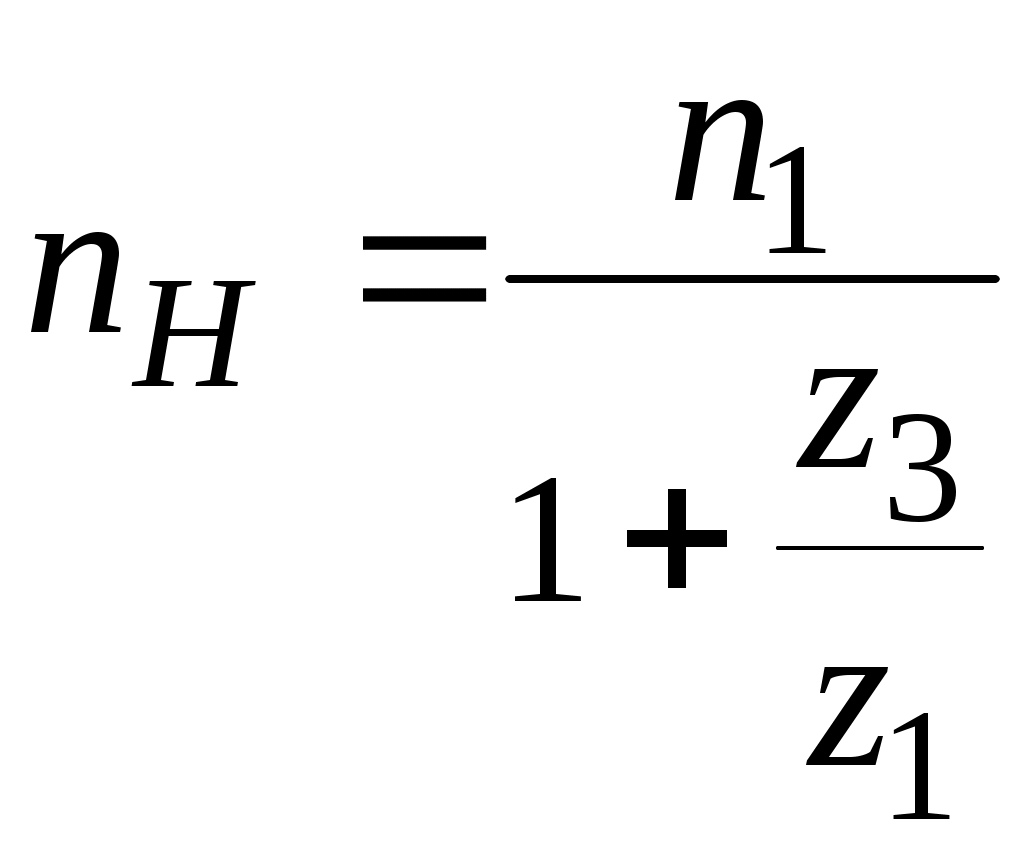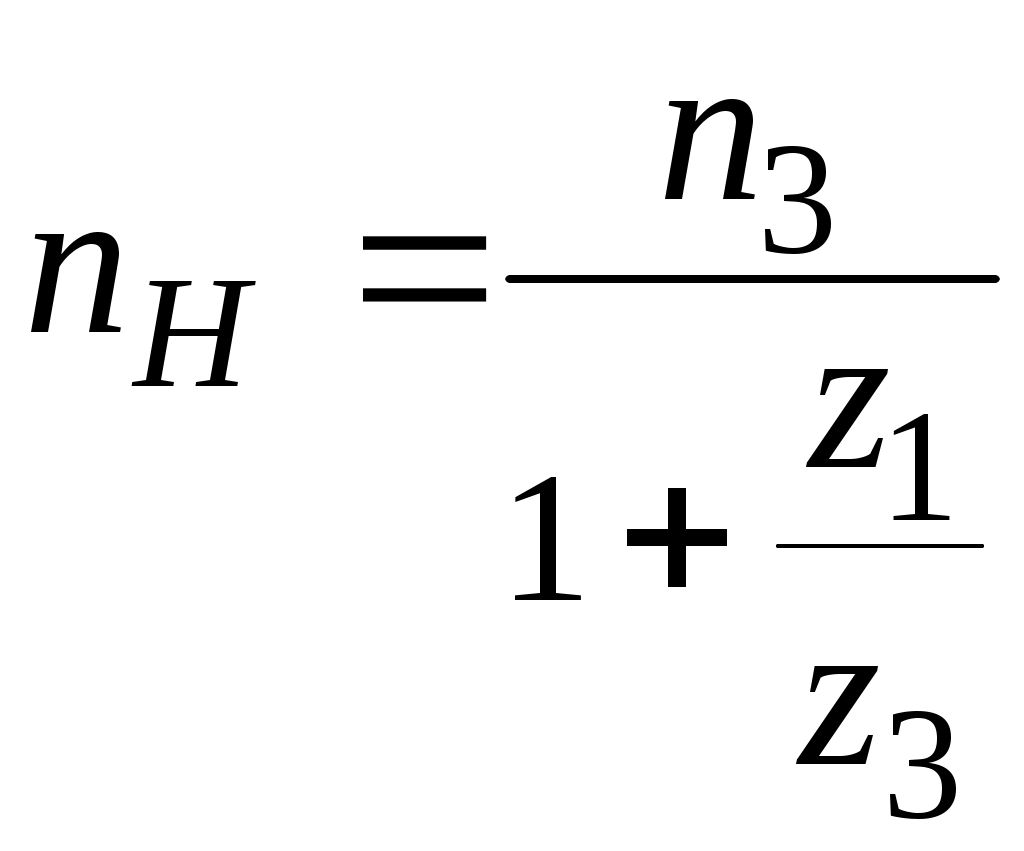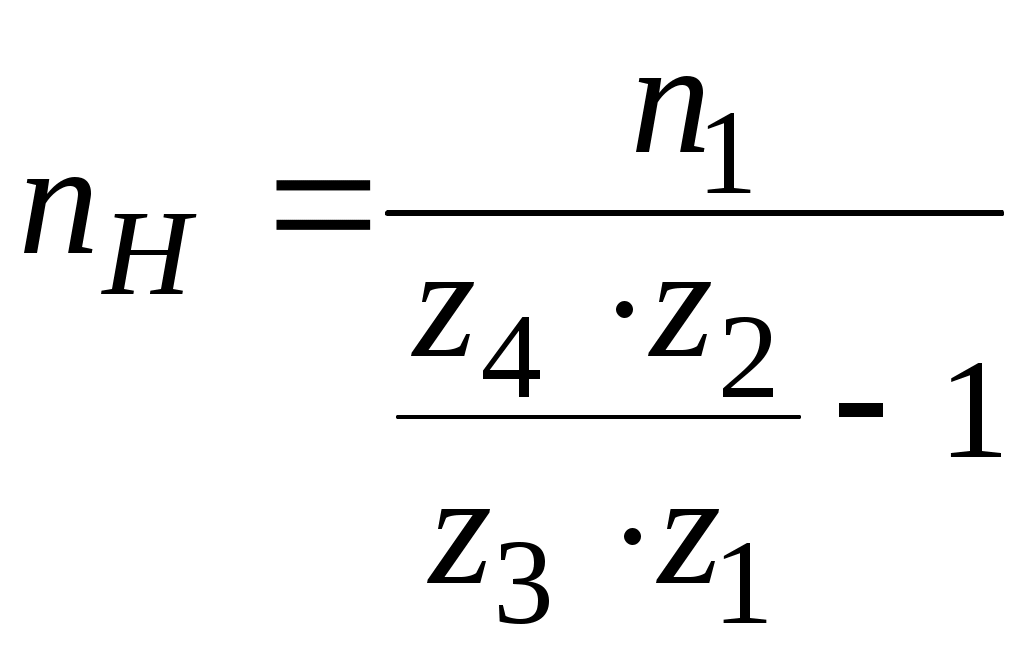Курсавая, планетарная передача. Кур раб планетарка ТММ. Методические указания предназначены для студентов, выполняющих расчетнографическую или курсовую работу по теории механизмов и машин
 Скачать 1.05 Mb.
|
|
Пример. Необходимо определить числа зубьев ступени №7 со сдвоенными сателлитами соблюдая условие соосности при  = 10. Отношение чисел зубьев равно:  1= 9.Так как колесо с числом зубьев  по размеру должно быть больше колеса с числом зубьев  (рис.7), то число D должно тоже быть больше числа C. Определяем путем подбора сомножители A,B,C,D:  9 .Отсюда имеем: D= 9, B= 1, C= 1, A= 1. Числа зубьев равны:  = 1∙(9–1) = 8;  = 1∙(9–1) = 8; = 1∙(1 + 1) = 2;  =9∙(1 + 1) = 18.Числа зубьев колес можно увеличить на одинаковое для всех сомножителей целое число, сохраняя при этом соосность колес. Для данного примера возможен другой вариант разбивки на сомножители: 9 .Отсюда имеем: D= 3, B= 3, C= 1, A= 1. Числа зубьев колес равны:  = 1 ∙ 2 = 2,  = 3 ∙ 2 = 6, = 1 ∙ 4 = 4, = 3 ∙ 4 = 12.При подборе чисел зубьев планетарных ступеней со сдвоенными сателлитами должно быть соблюдено условие соседства, заключающееся в том, что рядом расположенные сателлиты не должны касаться друг друга (рис.11).  Рис.11.Схема расположения сателлитов При этом количество сателлитов определяется из условия:  ,где  минимальный угол между сателлитами. Этот угол равен: =2 ,где  диаметр окружности вершин сателлита; диаметры начальных окружностей центрального колеса и сателлита соответственно. Для устранения возможности трения при касании цилиндров вершин соседних сателлитов предусматривают наличие между ними минимального гарантированного зазора  мм, тогда =2 .В случае сдвоенного сателлита  берётся для большего из них.При определении чисел зубьев планетарных ступеней необходимо учитывать также условие сборки. Условие сборки заключается в том, что зубья всех сателлитов должны быть во впадинах ответных колес. На рис.12 показано положение центральных колёс механизма при установке первого сдвоенного сателлита.  Рис.12.Схема расположения зубьев сателлита При выбранном значении число сателлитов  угол между ними  .Для того, чтобы установить при сборке второй сателлит под углом  к первому, повернём водило на угол  , который может быть равным  ,где  – любое целое число.При повороте водила на угол первое колесо повернётся на угол  .Для того, чтобы второй сателлит мог быть поставлен на место, которое занимал первый до поворота водила, необходимо чтобы первое колесо повернулось на целое число угловых шагов, что и обеспечивает одинаковое взаимное расположение зубьев центральных колёс  и  , т.е. .Подставляя первое и третье выражения во второе получим  ,откуда  .Из полученного следует, что если при каком-либо значении возможно получение целого значения С, то сборка механизма возможна.В простейшем случае сборки при =0. Тогда .Если ни при одном из значений значение С не будет целым, то сборка такого механизма невозможна и следует менять или числа зубьев.Для планетарных ступеней №3 – №6 при количестве сателлитов равном двум условие сборки выполняется всегда. Передаточное отношение от первого колеса к водилу для этих ступеней равно  .Тогда целое число определится из уравнения 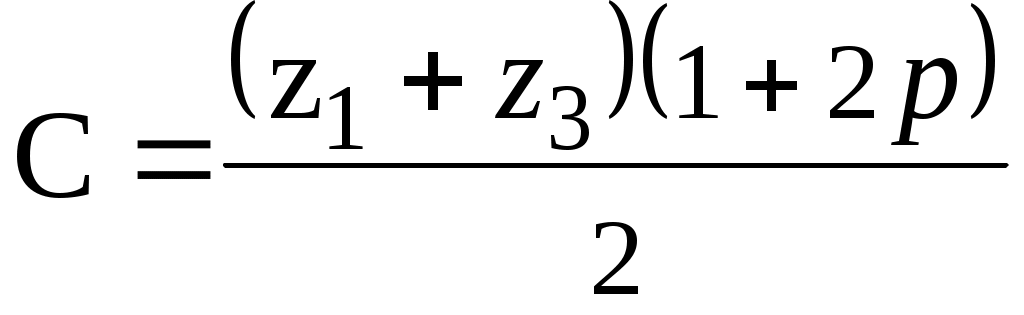 .Так как число зубьев  , то при нечетном числе число тоже нечетное, а при четном его значении – четное. Следовательно, сумма  кратна двум при любом значении чисел зубьев, а отсюда С является целым числом.За габаритные размеры редуктора при синтезе принимается наибольший размер одной из ступеней или ее частей (рис.13). 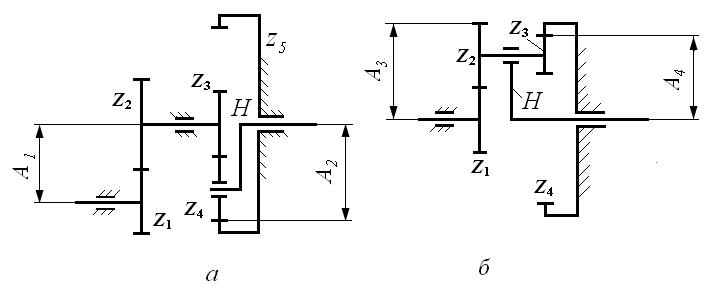 Рис.13.К определению габаритных размеров:а – комбинированного редуктора; б–ступени со сдвоенными сателлитами. Так как модули всех колес для каждого редуктора одинаковы, то габаритные размеры ступеней можно определить через соотношение чисел зубьев. Формулы для определения габаритных размеров различных ступеней приведены в табл.7 Таблица 7
Из двух вариантов редукторов в расчете выбирается редуктор с меньшими габаритными размерами. Для редуктора с минимальными габаритными размерами производится расчет чисел оборотов всех звеньев. Числа оборотов зубчатых колес различных ступеней определяются аналитическим методом по формулам, которые приведены в табл.8, и графическим способом. Таблица 8
Обозначения колес в табл.8 соответствуют рис.1 – 9. Угловая скорость колес может быть определена по формуле  ,где  число оборотов.Число оборотов или угловая скорость выходного звена редуктора не должны отличаться от заданного значения больше, чем на ± 5%. 4.Пример расчета Исходные данные для расчета: 1.Структурная схема комбинированного редуктора (рис.14). 2.Число оборотов на входе редуктора  об/мин. 3.Число оборотов на выходе редуктора  об/мин.4.Модуль зубчатых колес передачи 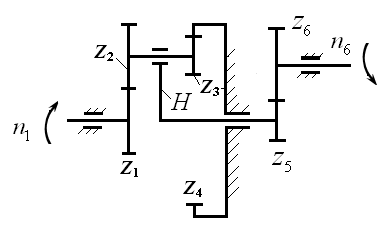 3 мм. Рис.14 Необходимо выполнить синтез данного планетарного редуктора (найти все  ) обеспечивающие работоспособность и заданные передаточные отношения.Решение. 1.Разбивка общего передаточного отношения по ступеням (первая ступень планетарная  и вторая ступень рядовая  ). ;  Обычно для такой планетарной ступени рекомендуется принимать  (см. табл.1). Для цилиндрической зубчатой передачи  3…7. Принимаем  15, тогда . |
