|
|
Контрольная работа по математике. Контрольная работа по математике (1 ч.). Задача Найти матрицу a Dab2C, b Fвв т а в с
ТИПОВОЙ РАСЧЕТ №1. ЛИНЕЙНАЯ АЛГЕБРА
Задача 1. Найти матрицу a) D=AB-2C, b) F=ВВТ
А = 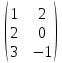 ; В = ; В = 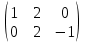 ; С = ; С = 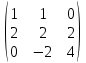
а) D=AB-2C
Найдем произведение матриц А и В:
АВ = 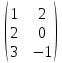 × × 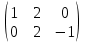 = = 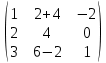 = = 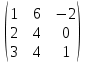
Найдем произведение числа 2 на матрицу С:
2С = 2 × 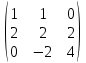 = = 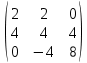
Найдем матрицу D
D = 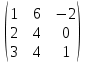 - - 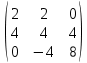 = = 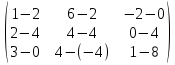 = =
= 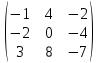
Ответ: D = 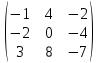
b) F=ВВТ
Найдем ВТ, для этого заменим строки матриц соответствующими столбцами
ВТ = 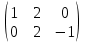 Т = Т = 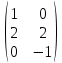
Найдем матрицу F=ВВТ
F = 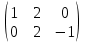 × × 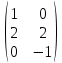 = = 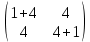 = = 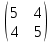
Ответ: F = 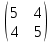
Задача 2. Решить невырожденные системы линейных уравнений с тремя неизвестными матричным методом, по формулам Крамера и методом Гаусса 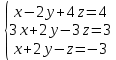
Решим данную систему матричным методом:
АХ = В Х = А-1В, где
А = 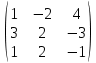 ; В = ; В = 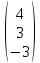
Вычислим А-1:
Найдем определитель матрицы А:
 = = 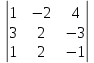 = -2 + 6 + 24 – 8 +6 – 6 = 20 ≠ 0 = -2 + 6 + 24 – 8 +6 – 6 = 20 ≠ 0
Поочередно найдем элементы матрицы А-1:
а11 = (-1)1+1 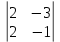 = 4 = 4
а12 = (-1)1+2 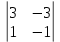 = 0 = 0
а13 = (-1)1+3 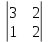 = 4 = 4
а21 = (-1)2+1 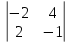 = 6 = 6
а22 = (-1)2+2 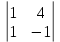 = -5 = -5
а23 = (-1)2+3 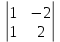 = -4 = -4
а31 = (-1)3+1 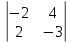 = -2 = -2
а32 = (-1)3+2 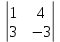 = 15 = 15
а33 = (-1)3+3 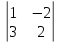 = 8 = 8
А-1 = 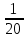 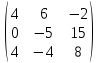
Х = А-1В = 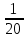 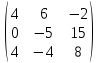 × × 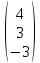 = = 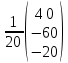 = = 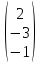 х = 2; х = 2;
у = -3; z = -1
Ответ: х = 2; у = -3; z = -1
Решим данную систему методом Крамера
Δ =  = 20 = 20
Δх = 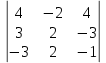 = -8 + 24 – 18 +24 +24 -6 = 40 = -8 + 24 – 18 +24 +24 -6 = 40
Δу = 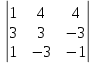 = -3 – 36 – 12 – 12 – 9 + 12 = -60 = -3 – 36 – 12 – 12 – 9 + 12 = -60
Δz = 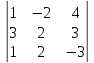 = -6 + 24 – 6 – 8 – 6 -18 = -20 = -6 + 24 – 6 – 8 – 6 -18 = -20
Х = 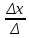 = = 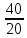 = 2 = 2
У = 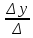 = = 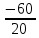 = -3 = -3
Z = 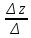 = = 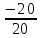 = -1 = -1
Ответ: х = 2; у = -3; z = -1
   Решим данную систему методом Гаусса Решим данную систему методом Гаусса
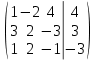 - *3 - - *3 - 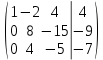 *2 - *2 -
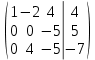 / (-5) / (-5)
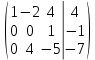 *(-4) + *5 + *(-4) + *5 +
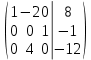 /4 (третью строку) /4 (третью строку)
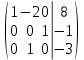 х = 2; у = -3; z = -1 х = 2; у = -3; z = -1
ТИПОВОЙ РАСЧЕТ № 2. ЭЛЕМЕНТЫ ОБЩЕЙ АЛГЕБРЫ
Задача 1. а) представить комплексное число в тригонометрической и показательной форме, изобразить на комплексной плоскости;
б) выполнить действие.
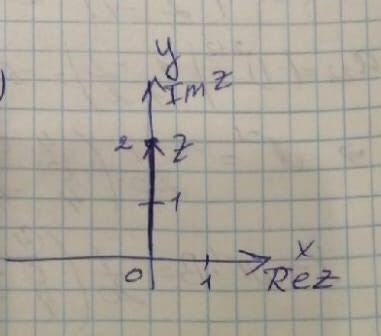
а) z = 2j
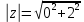 = 2 = 2
argZ = 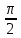 (т.к. х = 0, у > 0) (т.к. х = 0, у > 0)
Z = 2 (cos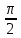 + jsin + jsin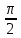 ) )
Z = 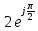
б) 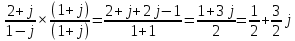
Задача 2. Найти корни уравнения, сделать проверку.
2x2 - 6x + 5 = 0
X1, 2 = 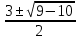 = = 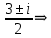 X1 = X1 = 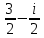 ; X2 = ; X2 = 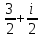
Выполним проверку: (Х – Х1)( Х – Х2) = 0
2 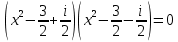
2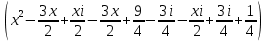 = 2x2 - 6x + 5 = 2x2 - 6x + 5
Задача 3. Разложите рациональную дробь на сумму простейших дробей
 R(x) = R(x) = 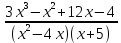
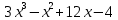 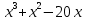
 - -
 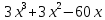 3 3
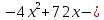 4 4
 R(x) = 3 + R(x) = 3 + 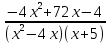 = 3 + = 3 + 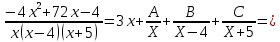
= 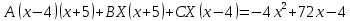
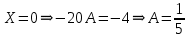
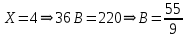
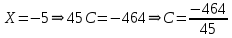
= 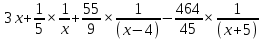
Ответ: 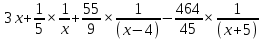
ТИПОВОЙ РАСЧЕТ № 3. ВЕКТОРНАЯ АЛГЕБРА
Задача 1. Найти:
1) координаты, модуль и направляющие косинусы вектора АВ;
2) скалярное произведение 4AB CD;
3) угол между векторами АВ и СD;
4) площадь треугольника АВС.
5) Объем пирамиды АВСD
A2;3;2, B4; 1; 2 , C6;3; 2 , D 5; 4;8 .
1) 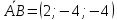 ; ;
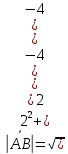 ; ;
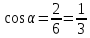 ; ; 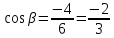 ; ; 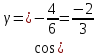
2) 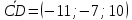
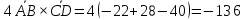
3)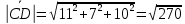
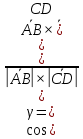
4) SABC = 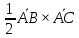
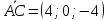
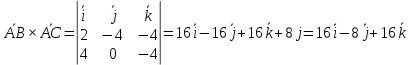
S = 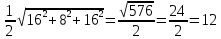
5) VABCD = 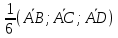
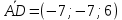
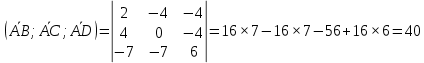
VABCD = 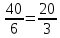
Задача 2. Выяснить, образуют ли векторы 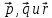 базис. Если образуют, разложить вектор базис. Если образуют, разложить вектор 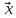 по это базису. по это базису.
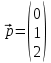 , , 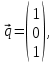 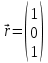 , , 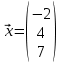
 = 1-1 = 0 не образует базис. = 1-1 = 0 не образует базис. 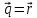 |
|
|
 Скачать 75.53 Kb.
Скачать 75.53 Kb.