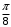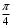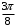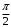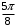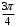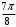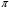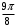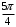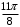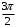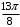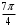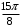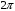ИРНИТУ Высшая математика, КР. 3804190207-1 математика решение (1). Задача Данную систему линейных уравнений решить тремя способами методом Крамера и методом Гаусса, и с помощью обратной матрицы
 Скачать 196.2 Kb.
|
|
Контрольная работа 1 Элементы линейной алгебры и аналитической геометрии Задача 1. Данную систему линейных уравнений решить тремя способами: методом Крамера и методом Гаусса, и с помощью обратной матрицы. 4. 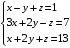 Решение: а) метод Крамера Вычислим определители , 1, 2, 4, где определители i находятся путём замены i-го столбца в главном определителе (составленном из коэффициентов при неизвестных) на столбец свободных членов с числами bi. 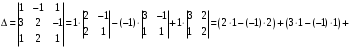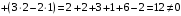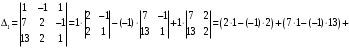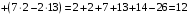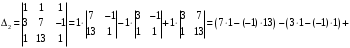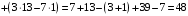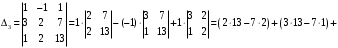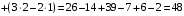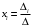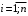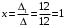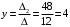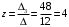Определители вычисляем разложением по элементам 1-й строки:   ,  ,  ,  ,по формулам Крамера  ,  , определяем значения неизвестных: ,  ,  .Ответ: x = 1, y = 4, z= 4. б) метод Гусса Чтобы привести расширенную матрицу данной системы 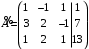 к треугольному виду, выполним следующие преобразования. 1. 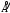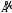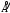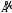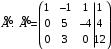Сформируем новую матрицу  , в первом столбце которой все элементы, кроме первого, равного 1, нули:– прибавим ко 2-й строке  строку 1, умноженную на (3), и поставим её 2-й в ;– прибавим к 3-й строке 1-ю, умноженную на (1), и поставим её третьей в : .Последняя матрица соответствует следующей системе: 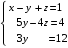 из которой определяем 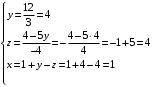 Ответ: x = 1, y = 4, z= 4. в) решение системы с помощью обратной матрицы Для решения системы матричным методом вводим матрицы 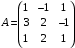 ,  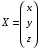,  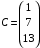.Тогда система запишется в виде матричного уравнения АХ = С. Умножив левую и правую части уравнения на А-1слева, получим А-1АХ= А-1С, где А-1– обратная матрица. Так как А-1А = Е, то Х= А-1С. 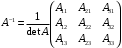 где 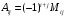 ; Aij– алгебраическое дополнение, соответствующее элементу aij; Mij– минор (определитель), который получается из матрицы А после вычеркивания i-ой строки и j-го столбца. Найдем алгебраические дополнения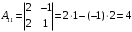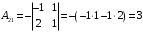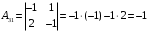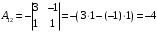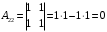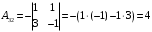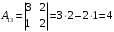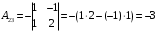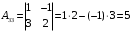:  ;  ;  ;  ;  ;  ;  ;  ;  .Следовательно, 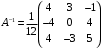 .Пользуясь правилом умножения матриц, получим решение системы: 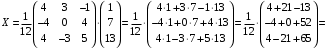 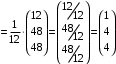 ,  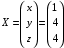.откудаx = 1, y = 4, z= 4. Сравнивая ответы, полученные при решении системы методом Гаусса и матричным методом, видим, что они совпадают. Ответ: x = 1, y = 4, z= 4. Задача 3. Линия задана уравнением в декартовой прямоугольной системе координат. Требуется: 1) перевести уравнение кривой в полярную систему координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс–с полярной осью; 2) построить линию по точкам начиная от = 0 до = 2, придавая значения через промежуток /8. 4. 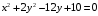 .Решение: Переведѐм декартовые координаты в полярные. Подставляя 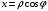 ,  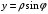в заданное уравнение, получим следующее выражение: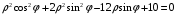 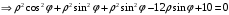 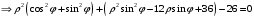 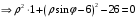 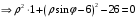то уравнение линии в полярных координатах имеет вид: 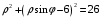 Для построения линии в полярной системе координат составим r таблицу значений полярного радиуса при определенных значениях полярного угла:
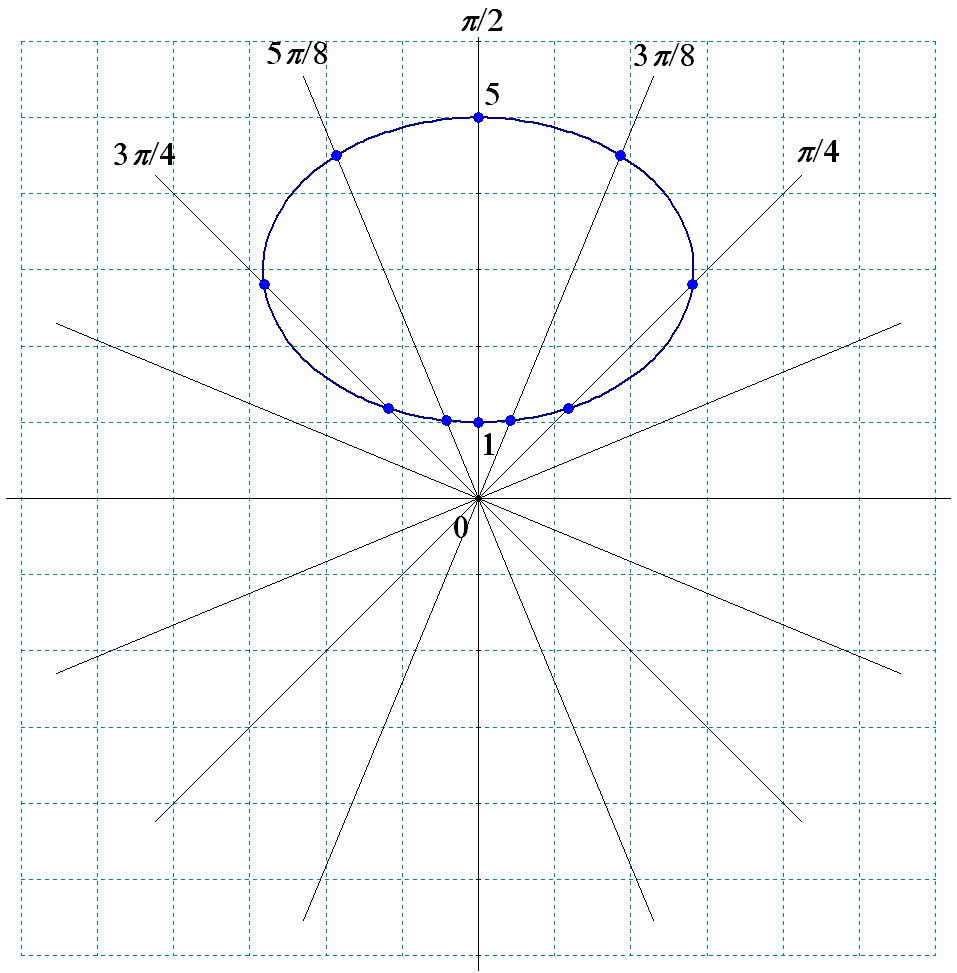 Рис. 1. Контрольная работа 2 Интегральное исчисление функции одной переменной Задача 12. Вычислить несобственный интеграл и исследовать его на сходимость. 4. 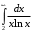 .Решение: Несобственный интеграл первого рода (по бесконечному промежутку) от правильной рациональной дроби может быть вычислен согласно определению несобственного интеграла первого рода. 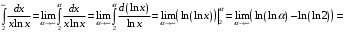 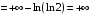 .Ответ:Несобственный интеграл расходится. |
