Нагнетатели и тепловые двигатели .(КП). Методическое пособие и задания к курсовому проекту по дисциплине Нагнетатели и тепловые двигатели

• Название: Методическое пособие и задания к курсовому проекту по дисциплине Нагнетатели и тепловые двигатели
• Дата: 23.11.2020
• Размер: 1.27 Mb.
• Имя файла: Нагнетатели и тепловые двигатели .(КП).doc
• Тип: Методическое пособие; #153042
• страница: 2 из 5

4. Профилирование лопасти

Как следует из основного урав­нения работы лопастного колеса, напор, создаваемый им, за­висит только от соотношений пара­метров потока на входе и выходе лопасти. Характер течения в меж­лопастных каналах как бы не вли­яет на процесс передачи энергии газу.

В действительности это не так. Анализируя выражение для u₂, c_2u, можно видеть, что форма лопасти (кривизна скелета) оказывает влия­ние на циркуляцию рабочего тела в межлопастных каналах и, сле­довательно, на величину H_т. По­этому для повышения эффективно­сти работы колеса лопасти должны иметь рациональную форму, обес­печивающую минимум потерь.

Профилирование лопасти состо­ит из построения скелета (средней линии, рис.3,б) с последующим наращиванием ее толщины s, кото­рая из технологических соображе­ний зачастую принимается постоян­ной по длине скелета. Известно не­сколько методов профилирования лопасти. Рассмотрим некоторые упрощенные способы построения скелетной лопасти.
Лопасть, очерченная дугой окружности

Схема построения простейшей формы скелета лопасти приведена на рис. 3,а.

По теореме косинусов из тре­угольников 00' А и ОО'Б радиус R_л скелета лопасти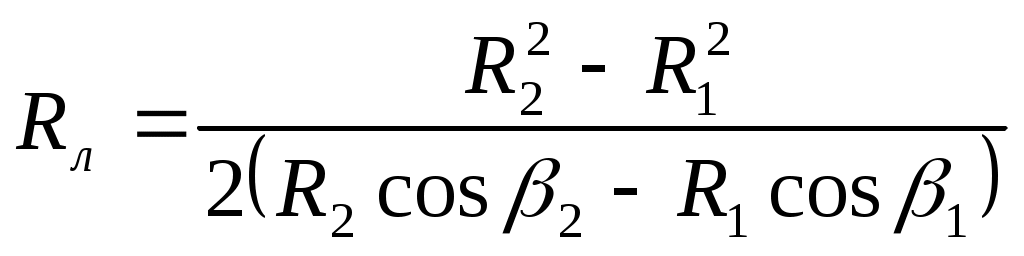

(17)

Геометрическое место центров дуг окружностей лежит на окруж­ности радиуса R₀:

(18)

Длина хорды АБ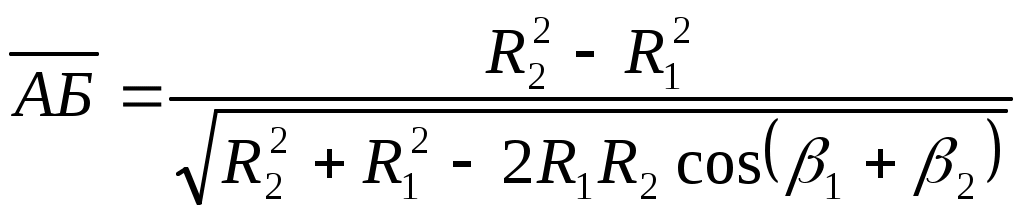

(19)
Центральный угол ν лопасти

(20)

Длина скелета лопасти



Здесь ν — в градусах.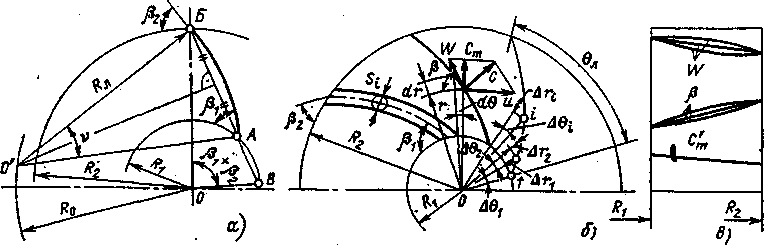

Рис. 3. Профилирование лопасти:

а — очерченной дугой круга; б — построенной по точкам

Построение лопасти производит­ся в таком порядке. От радиуса ОБ под углом β₁ + β₂ проводят луч ОВ до пересечения с окружностью ра­диуса R₁. Точку В соединяем с точ­кой Б и получаем точку А начала лопасти. Хорду АБ делим на два одинаковых отрезка. Через середи­ну отрезка АБ проводим перпенди­куляр до пересечения с окруж­ностью радиуса R₀ (точка 0'). Ра­диусом R_л описываем дугу АБ.
Профилирование лопасти по точкам

Если задаться зависимостью (рис. 3,б) в пределах значений от β₁ до β₂, то графиче­ским интегрированием, постепенно .переходя на малые значения Δ_r и строя соответствующий угол β, можно спрофилировать всю лопасть. Интегрирование можно произвести аналитически, что значительно упро­щает задачу, в частности, при ис­пользовании ЭВМ.

Сечение цилиндрической лопасти в плане можно считать истинным сечением поверхности тока. Диффе­ренциальное уравнение скелета ло­пасти в плане имеет вид

(21)

Интегрируя выражение (21) в пределах от R₁ до R₂, получим пол­ный угол охвата лопасти в плане, град: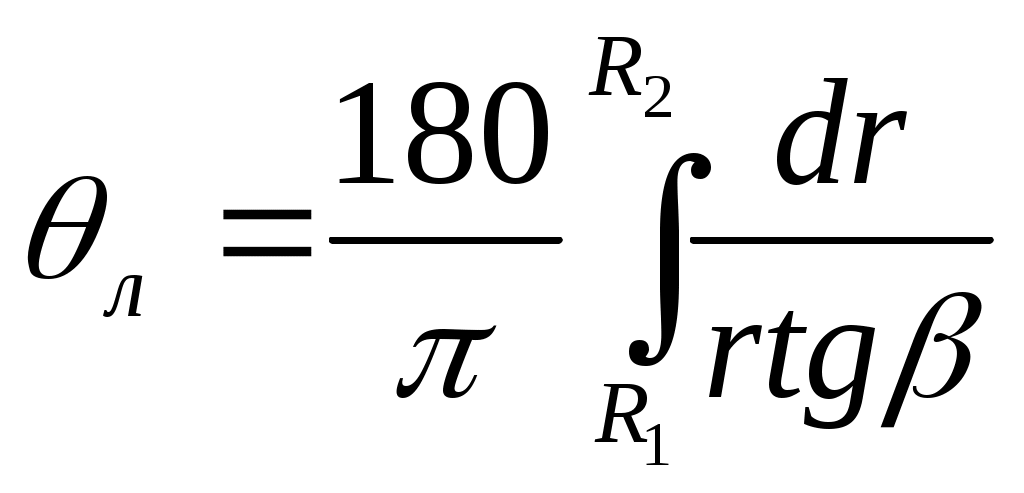

(22)

Угол установки лопасти β на любом радиусе можно определить по известному (выбранному) рас­пределению скорости W и мериди­анной скорости без учета стес­нения, а также изменения толщины лопасти s по радиусу (рис.3):

(23)

Для лопастей, загнутых назад (β₂ < 90°), оправдывает себя ли­нейный закон изменения относи­тельной скорости W или угла β. При выпуклой кривой W=f(r) (кривая β=f(r) - вогнутая) про­исходит увеличение длины l лопасти, и наоборот.

Интегрирование выражения (21) удобно производить таблич­ным способом. Обозначив подынтег­ральную функцию через В = 1/r tg β, для любого промежуточ­ного радиуса r_к можно определить угол θ_К, град:

(24)

Порядок вычисления координат r_i и θ_i; скелета лопасти приведен в табл. 2.

Для построения скелета лопас­ти необходимо выбрать n = 10 ÷ 12 точек. Угол охвата лопасти в плане обычно θ_Л = 70 ÷ 90°. По полученным координатам скелета ло­пасти подбирают два-три радиуса и описывают среднюю линию. Из то­чек средней линии проводят окруж­ности диаметрами s_i. Огибающая ок­ружностей представляет собой кон­тур лопасти в плане. Как правило, лопатку выполняют постоянной тол­щины. Входную кромку лопасти заоваливают радиусом r₁ = 0,5s или выполняют переменной толщи­ны на участке l(4—5)s (см. рис. 3, б).

Известны также другие методы построения лопасти, основанные на соответствующих допущениях, на­пример: постоянство замедления от­носительной скорости по радиусу, постоянство давления в поперечных сечениях межлопастного канала. Разработаны также газодинамиче­ские методы профилирования лопа­стей с использованием схемы заме­ны скелетов лопастей системой при­соединенных вихрей, индуцирующей требуемое поле скоростей в рабо­чем колесе.
Таблица 2.

Профилирование лопасти по точкам

№ точ- ки	r, мм	мм	s, мм	м/с	W, м/с	sin β	β	tg β
1 …………………………………………………………………………………………. n

Особенности расчета и профилирования рабочих

колес с пространственными лопастями

С увеличением n_уд изменяется форма осевого сечения рабочего колеса в основном за счет увеличе­ния ширины b₂ и уменьшения отно­шения D₂/D₀. При D₂/D₀ ≤ l,6 входную кромку лопасти распола­гают в зоне поворота потока (рис.4). В этом случае профили­рование лопасти по средней струй­ке не обеспечивает хорошего согла­сования ее с потоком, так как углы натекания потока β_пi; сильно изме­няются по длине входной кромки. Углы установки лопасти на входе нужно согласовывать с углами по­тока, чтобы обеспечить безударный вход. Углы установки лопасти по длине входной кромки возрастают от покрывающего диска к основно­му β₁₀ > β_1п частично за счет уве­личения углов атаки δ₀ > δ_п. По­верхность лопасти принимает про­странственную форму (двойной кривизны), которая обычно распро­страняется на часть лопасти, при­легающую к входному участку. Для улучшения условий работы отводя­щих устройств лопасть имеет на выходе цилиндрическую форму.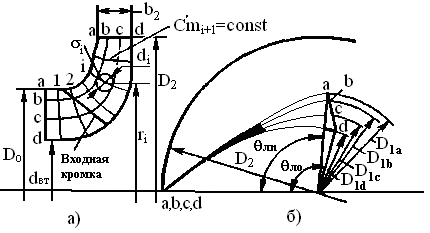



Рис. 4. Схема колеса с пространственной лопастью:

а — продольная проекция; б — план лопасти
Пространственные лопасти обы­чно применяются при коэффициен­тах расхода по условиям входа φ₁> 0,06.

Построение пространственной лопасти можно осуществить упро­щенным способом. Поток в рабочем колесе делят на n = 3 ÷ 5 элемен­тарных потоков поверхностями то­ков, имеющими форму поверхности вращения. В осевом сечении по­верхности токов представлены ли­ниями, делящими колесо на элемен­тарные составляющие. В качестве линии деления часто принимаются линии тока равноскоростного пото­ка, вписываемого в меридианное осевое сечение рабочего колеса (рис. 4, а).

При равноскоростном потоке должно выполняться условие ра­венства объемного расхода через каждое «элементарное колесо». Для построения равноскоростного пото­ка выбирают два граничных сече­ния и разбивают их на равновели­кие участки. Для участков на входе в колесо должно выполняться условие , где , а . Сечение на выходе из колеса делит­ся на участки шириной b₂/i. В рас­сматриваемом случае i=3. (число участков). Поток строят методом последовательных приближений.

Через полученные точки деления (а, b, с, d) проводят ориентировочно линии тока s_i. Одну из ограничивающих линий делят на отрезки, через которые проводят линии σ_i, ортогональные к другим линиям тока. Для каждой линии σ_i должно выполнятся условие с_тi = соnst.

Объем газа, проходящий через любое сечение I ортогональной поверхности, определяется суммированием элементарных расходов:

.

Интеграл удобно определять численным интегрированием, порядок которого для одной из линий δ_i приведен в табл. 3. Такие вычисления необходимо проводить для каждой ортогональной линии.

По полученным (с учетом знака) значениям δd_i вносят коррективы путем взаимного изменения линий тока и ортогональных линий. Отклонение величин δd_i по ортогональной линии до 5 % считается допустимым. Если поток строят не в масштабе 1 : 1, то при определении значений с_тi необходимо ввести масштабный множитель. Поток можно построить при помощи ЭВМ по несложной программе.

После построения потока строят графики изменения меридианной скорости без учета стеснения вдоль каждой линии тока, на основании которых получают гра­фики , используемые в дальнейшем при профилировании лопасти.

Лопасть двойной кривизны про­филируют по нескольким линиям тока, в качестве которых часто ис­пользуют линии а-а, b-b и т. д. Ме­тоды профилирования в принципе повторяют методы, применяемые для цилиндрических лопастей. По форме и взаимному расположению линий тока в плане можно су­дить о плавности формы лопасти (рис. 4, б).

Расчет рабочего колеса по методу подобия

Довольно распространенным яв­ляется способ расчета рабочих колес с использованием атласа экс­периментально отработанных модельных (индекс «м») рабочих ор­ганов. По полученному на заданные параметры V, Н_п, n значению n_УД в атласе подбирают необходимые модельные рабочие органы. Определяющим при этом является геометрическое подобие конструк­ции, нахождение требуемого n_УД в оптимальной по КПД зоне модель­ной характеристики и определенная форма напорной характеристики .

На модельной характеристике в режиме требуемого n_УД определя­ют параметры V_М и Н_ПМ, по кото­рым с учетом заданных V и H_п на­ходят масштаб геометрического подобия (коэффициент пересчета линейных размеров):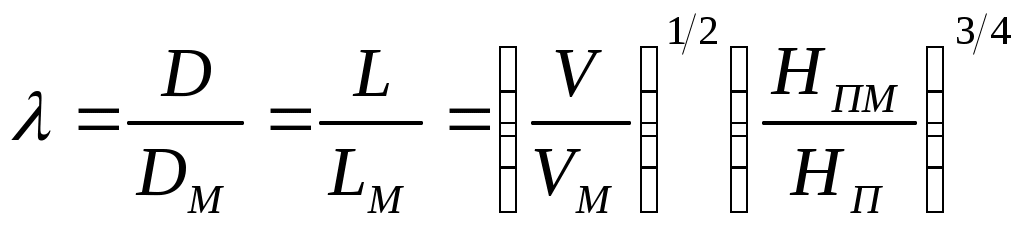

(25)

Таблица 3.

Построение равноскоростного потока

Линии тока	ri, мм	di, мм	ridi, мм2	δ(ridi)=ridi – (ridi) ср	,мм	, м·с
а=а b=b c=c d=d

Примечание. ; .

Углы лопастей рабочего колеса при пересчете остаются неизменны­ми. Пересчет по выражению (25) дает достоверные результаты при λ ≤ 2 и сжатии при соблюдении ус­ловий подобия газов.

Пользуясь выражением (25) по имеющимся размерам модельных рабочих орга­нов можно определить размеры проектируемого колеса и построить расчетные характеристики.

Выражение (25) пригодно для пересчета и других элементов про­точной части компрессора.

4. Расчет отводящих устройств

Геометрические размеры и фор­му каналов отводящих устройств различных типов обычно определя­ют из условия согласования с пото­ком за рабочим колесом на расчет­ном (номинальном) режиме рабо­ты. Физическую модель течения газа за рабочим колесом можно представить суммированием двух потоков — источника и вихря. Тра­ектория движения частиц газа та­кого суммарного потока представ­ляет собой спираль. Пренебрегая влиянием трения газа о стенки от­вода и принимая допущение по­стоянства момента скорости с_ur=idem, считают, что частичка га­за движется в отводе по спирали с постоянным углом а в любой точке. Для уменьшения потерь ограничи­тельная стенка отвода выполняется по спирали с углом а, равным углу абсолютной скорости a в непос­редственной близости за рабочим колесом.

Спиральный отвод. Спиральные отводы применяются в компрессо­рах с различным количеством сту­пеней. В многоступенчатых машинах они нашли применение в кон­цевых ступенях.

Спиральный отвод представляет собой канал, окружающий рабочее колесо поперечным сечением, уве­личивающимся в направлении вра­щения вала компрессора. Цилинд­рическая площадь входного сече­ния канала равна F₃=πD₃b₃. Диа­метр D₃ и ширину b₃ спирали вы­бирают по соотношениям D₃/D₂=1,1÷1,2, а b₃/b₂ = 1,25 ÷ 2,0. При увеличении угла a₂ значения D₃/D₂ уменьшаются, а b₃/b₂ увели­чиваются.

Ограничивающая внутренняя по­верхность отвода очерчивается по спирали (рис. 5). Начальный участок спирали очерчивается под углом a₃:

, (26)

где — радиальная составляющая абсолютной скорости на входе в спираль; — окружная состав­ляющая абсолютной скорости при входе в спираль.

Объемный расход при входе в спираль определяется выражением

,

где (степень повышения давления в ступени).

Расчет и профилирование спи­ральной части отвода сводится к определению поперечных проходных сечений спирали.

Исходными данными для рас­чета служат D₃, b₃, a₃ и форма по­перечного сечения. Геометрические размеры сечений также зависят от характера изменения скорости газа по спирали c = f(r, φ). Угол охва­та спирали обычно выбирается в пределах φ_сп = 330 ÷ 340°. Число расчетных сечений выбирается рав­ным i= 8 ÷ 12. В рассматриваемом случае i = 8.

Для обеспечения осесимметричного движения за рабочим колесом необходимо, чтобы для потока газа в спирали выполнялось условие с_иr = idem, указывающее на гипер­болический закон распределения скорости с_и.

Для построения спирали необхо­димо выбрать форму поперечного сечения. Наибольшее распростране­ние получила трапециевидная фор­ма сечения (рис. 5,а).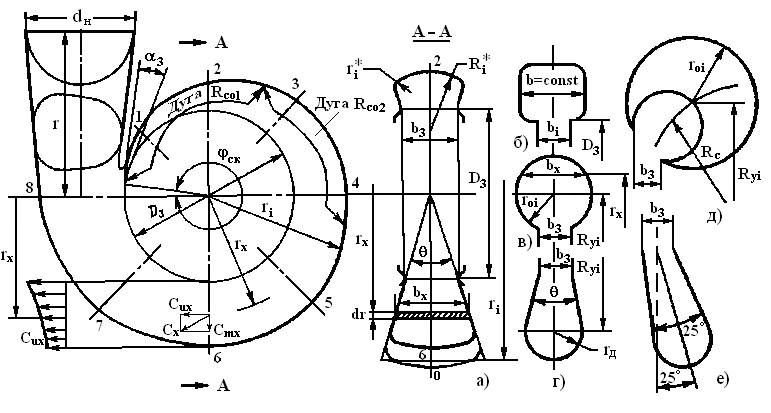



Рис. 5. Спиральный отвод: а — трапециевидное сечение; б— прямоугольное; в— кругло; в—грушевидное; д —круглое несим­метричное; е — грушевидное несимметричное

Боковые стенки могут быть пло­скими. Прямоугольное сечение (рис. 5, б) предпочтительно по технологическим соображениям. Часто применяется сечение в виде круга (рис. 5, в), как наиболее благоприятное в газодинамическом отношении.

Разновидностью круглого явля­ется грушевидное сечение (рис. 5, г). Как показали экспе­риментальные исследования, сече­ния канала, ось которых не совпа­дает с осью рабочего колеса, обес­печивают меньшие потери за счет
лучшего согласования с потоком на выходе рабочего колеса. В качест­ве примера приведены круговая (рис. 5,д) и грушевидная (рис. 5,е) формы несимметрич­ных сечений спирального канала.

Для, построения спирального ка­нала обычно используются два ос­новных метода расчета:

из условия постоянства момента скорости с_иr = idem. В этом слу­чае с_и по окружности произвольно­го радиуса г не изменяется;

по заданному закону распреде­ления средней скорости c_срi в сечениях спирали по углу φ. Обычно принимают с_ср = const.

В этих случаях расход через се­чения спирали меняется пропорцио­нально углу охвата φ_i:



Элементарный расход через сечение



а суммарный расход через i-e сече­ние определяется интегрированием: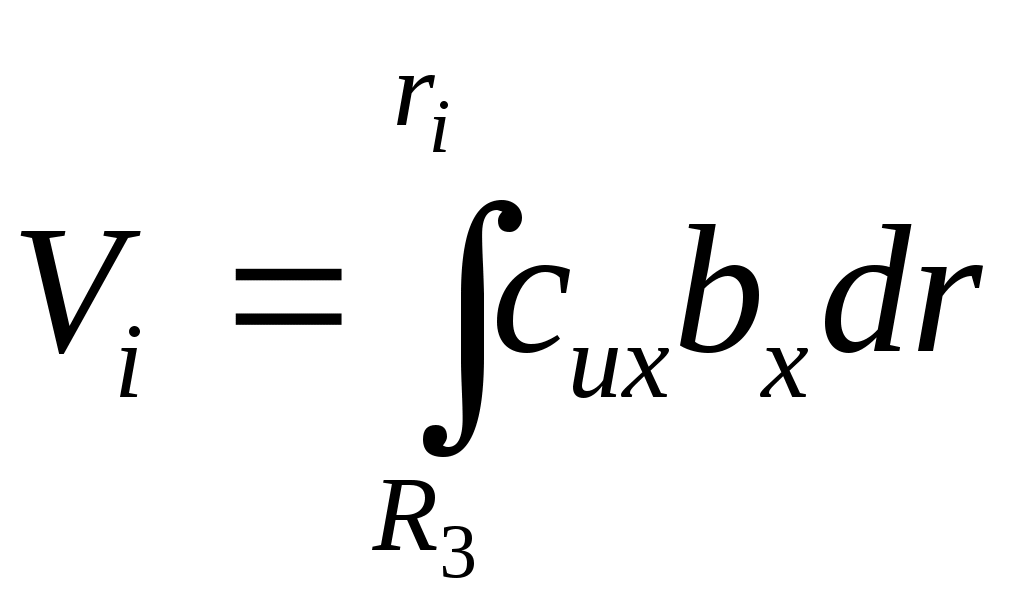

(27)

Для вычисления интеграла не­обходимо знать закон изменения с_ux = f(r_x) и b_x =f(r_x).

В практике компрессоростроения получил распространение метод построения спирали по закону c_ur = idem . Приближенный расчет проводят без учета вязкости и сжи­маемости газа, так как эти факторы оказывают противоположное влия­ние на размеры канала. Однако из­вестны уточненные методы расчета спирали с учетом вязкости и сжи­маемости газа.

Выражение (27) в этом случае принимает вид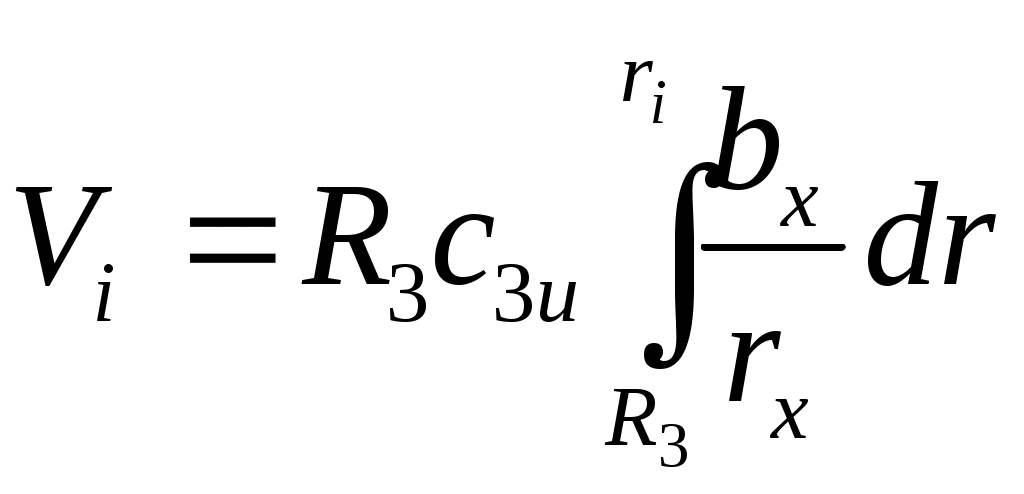

(28)

При сложной зависимости b_х= f(r_x) интеграл (28) удобно ре­шать графически.

Для частных случаев значение интеграла получают аналитически.

1). Для трапециевидного сечения (рис. 5, а)

(29)

(30)
2). Для прямоугольного сечения (рис. 5,б)

b = const

- логарифмическая спираль.

Для учета сокращения площади сечения из-за скругления углов не­обходимо увеличивать r_i/R₃ на 1-2 %. Если наружная стенка сечения очерчена радиусом R_i^*, то для каждого сечения необходимо графически подобрать радиусы R_i^* и r_i^*, чтобы обеспечить равенство площадей (заштрихованы по-разному
на рис. 5,а).

3). Для круглого сечения (рис. 5, в)



При построении спирального от­вода с круглым поперечным сече­нием удобно определить г₀ по за­данному углу φ. Принимая во внимание, что R_y = R₃ + r₀, имеем

(31)

где (32)

4). Для несоосного круглого се­чения (рис. 5, д) при построении отвода целесообразно использовать выражение

(33)
5). Для сечений (рис. 5, г и е) следует применять графоаналити­ческий метод расчета.

Задаваясь значениями r₀ и вы­бирая R_v по конструктивным сооб­ражениям, вычисляем φ и строим графики φ = f(R_y) и φ = f(r₀), на основании которых для требуемых φ_i определяем величины R_y и г₀.

Построение спирали производим в следующей последовательности.

Пользуясь аналитическими за­висимостями или графоаналитиче­ски определяем размеры конечного 8-го сечения (горловины) спирали (для φ_сп). В соответствии с выра­жением (28) получаем величину r₈. Затем эту операцию повторяем для каждого сечения φ_i и получаем соответствующие значения r_i. Из указанных выше соображений под­бираем радиусы закруглений r_i^* и R_i^*. На радиусе r_i под соответст­вующими углами делаем засечки. Полученные точки сопрягаем тре­мя-четырьмя дугами конструктивно подобранными радиусами R_спi.

Спиральный канал отвода за­канчивается диффузорным патруб­ком, который имеет по длине пере­менную форму сечения (от сечения 8 до круглого сечения нагнетатель­ного патрубка).

Угол расширения диффузора не должен вызывать отрыва потока при преобразовании в нем кинети­ческой энергии в давление. Диффузорность обычно определяется по приведенным диаметрам:

(34)
где F₈ — площадь 8-го сечения.