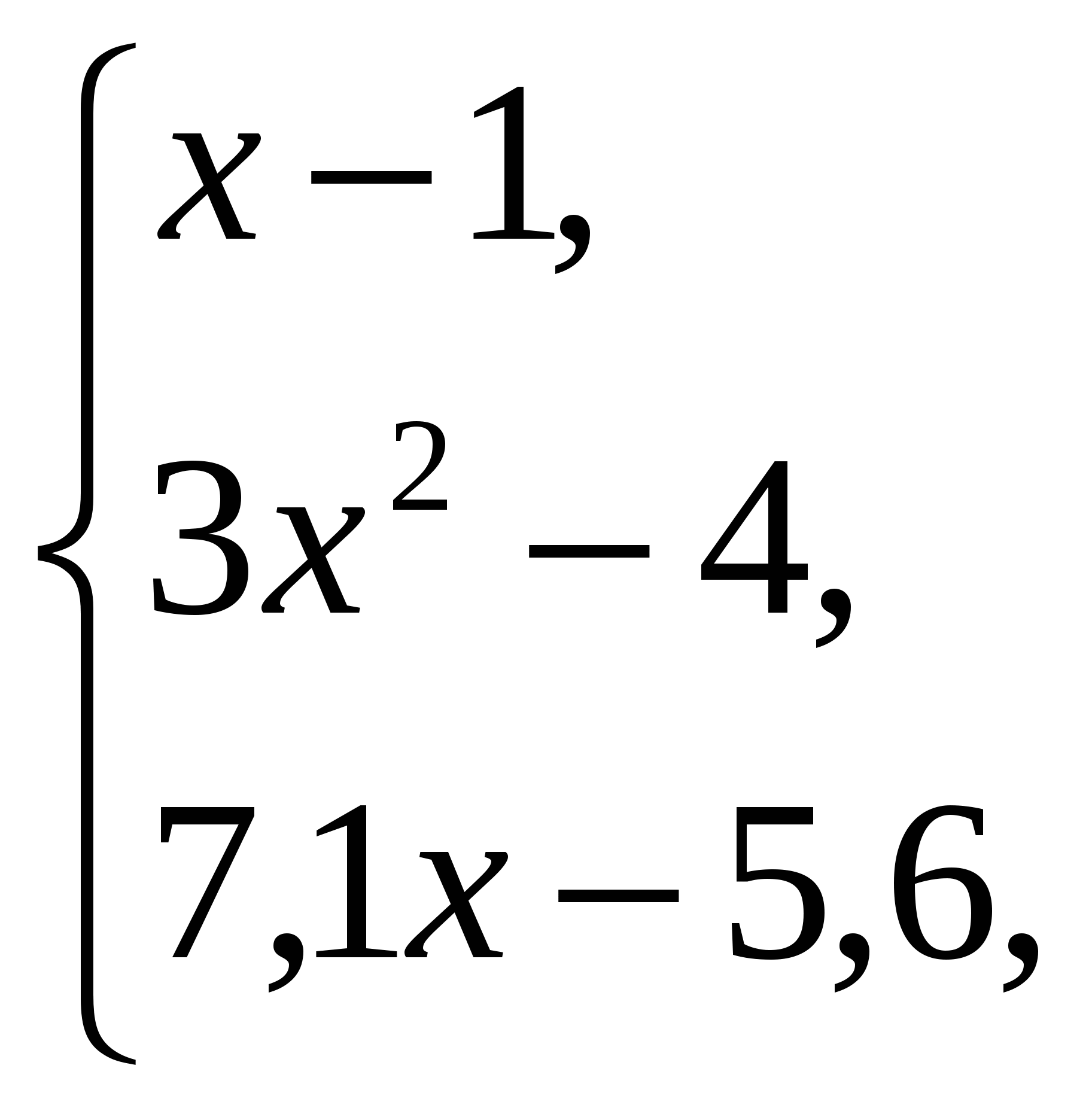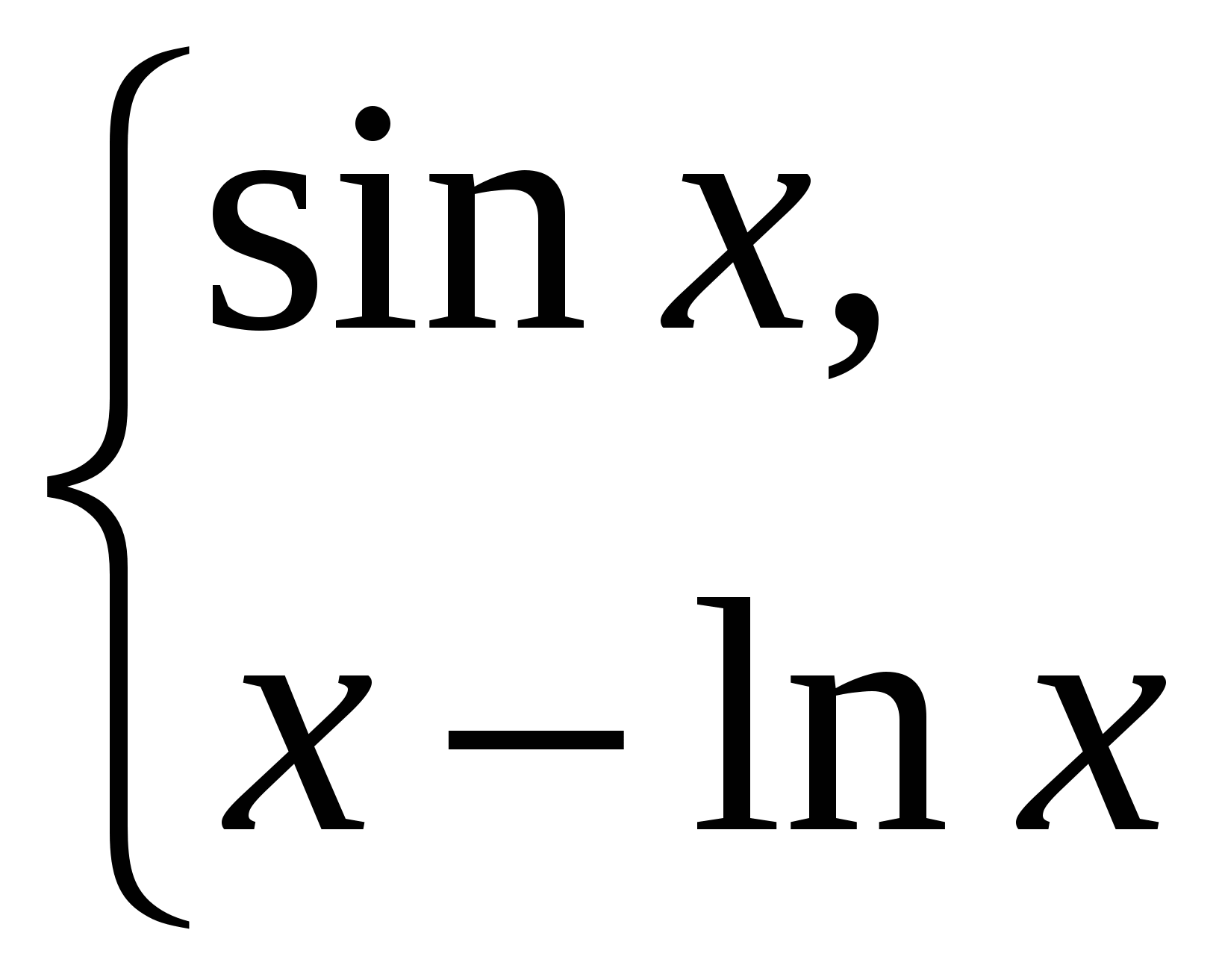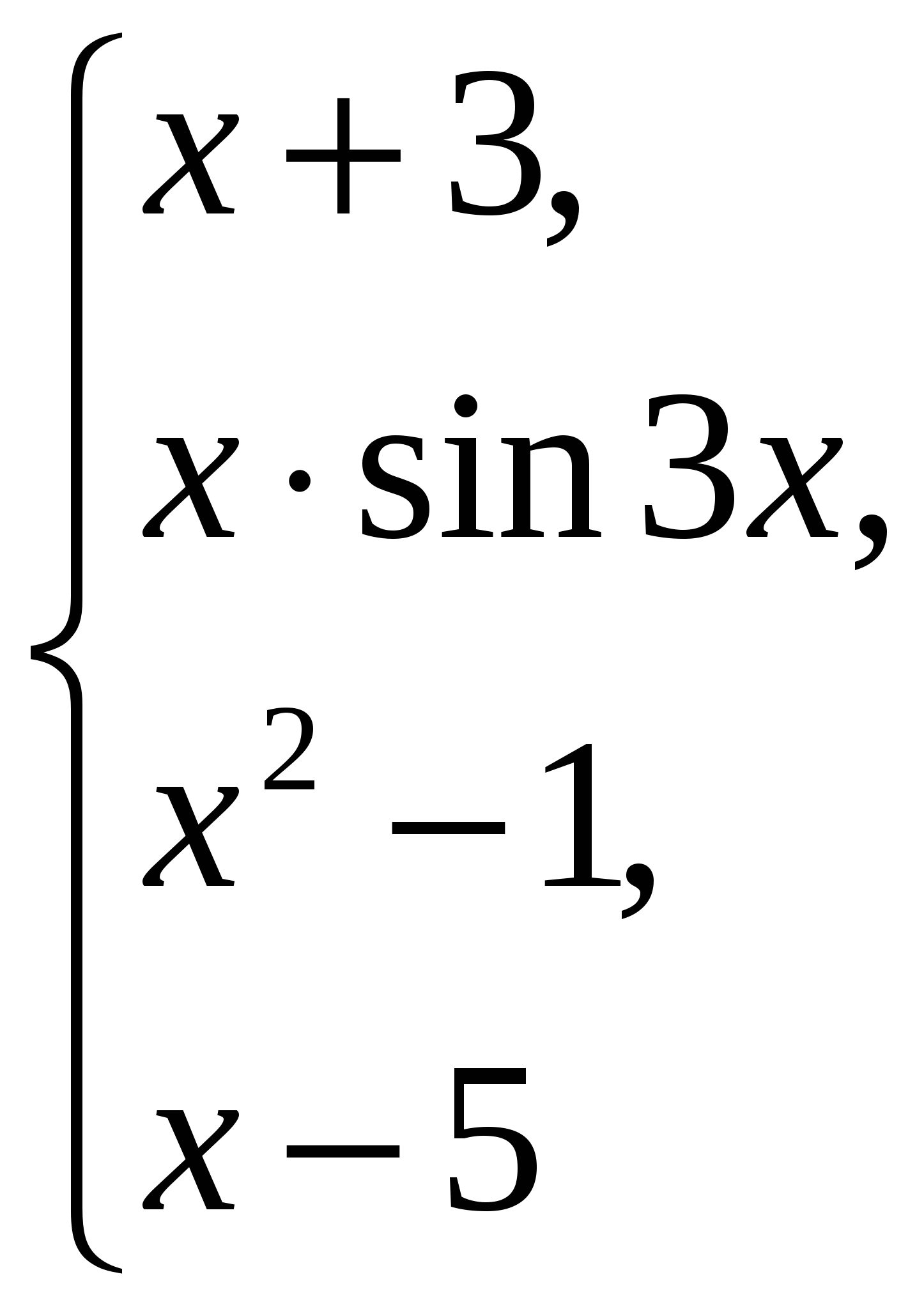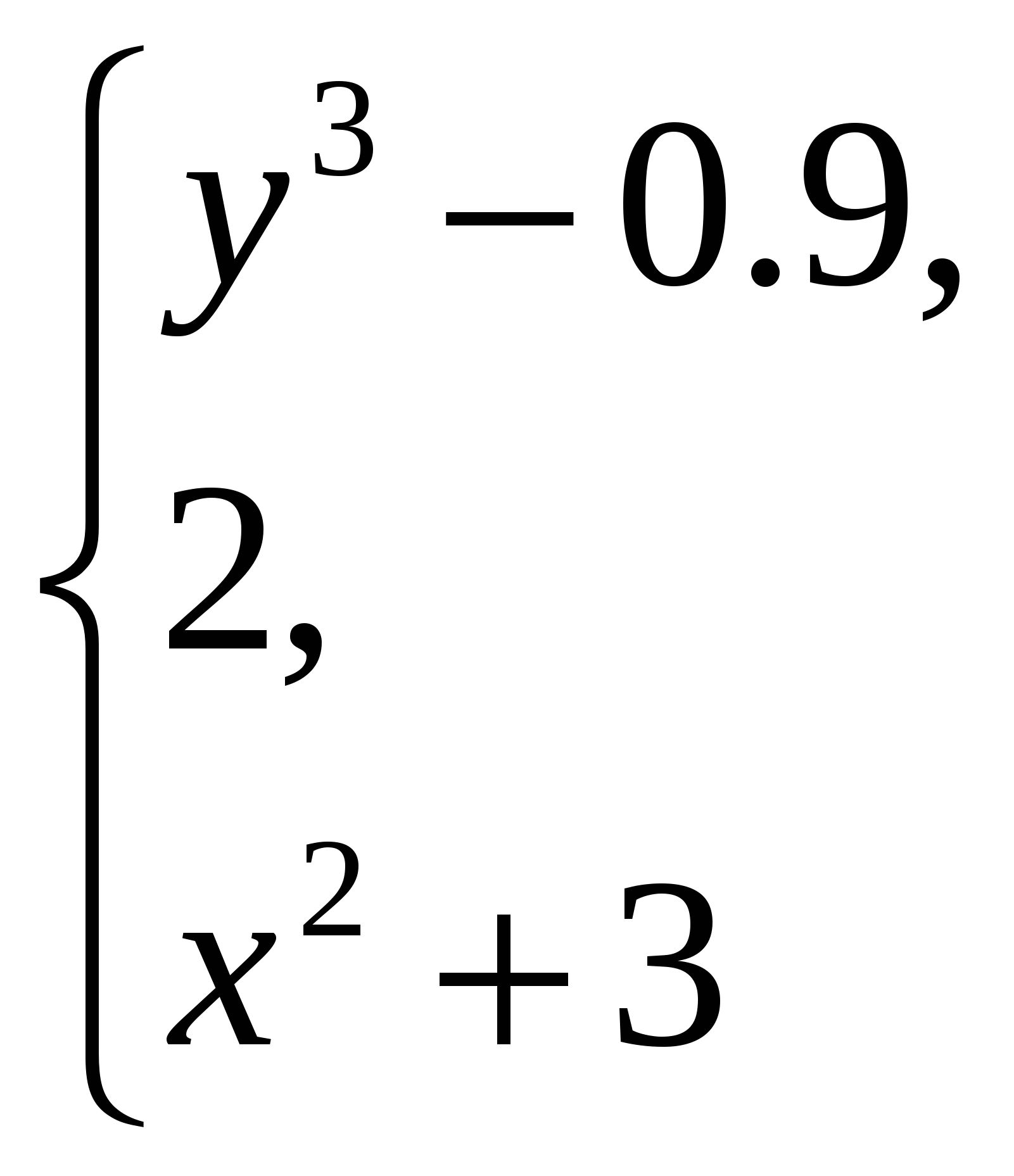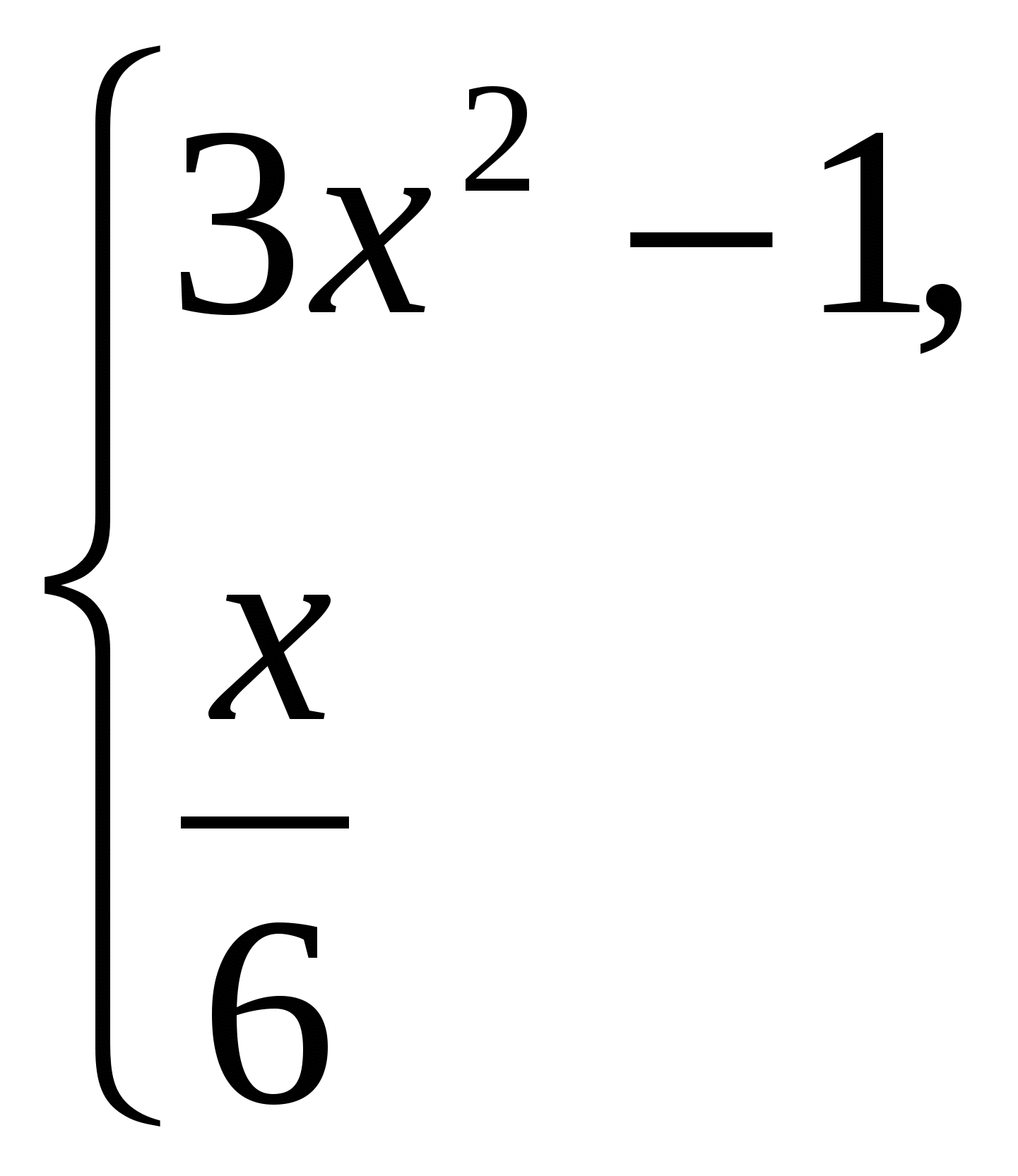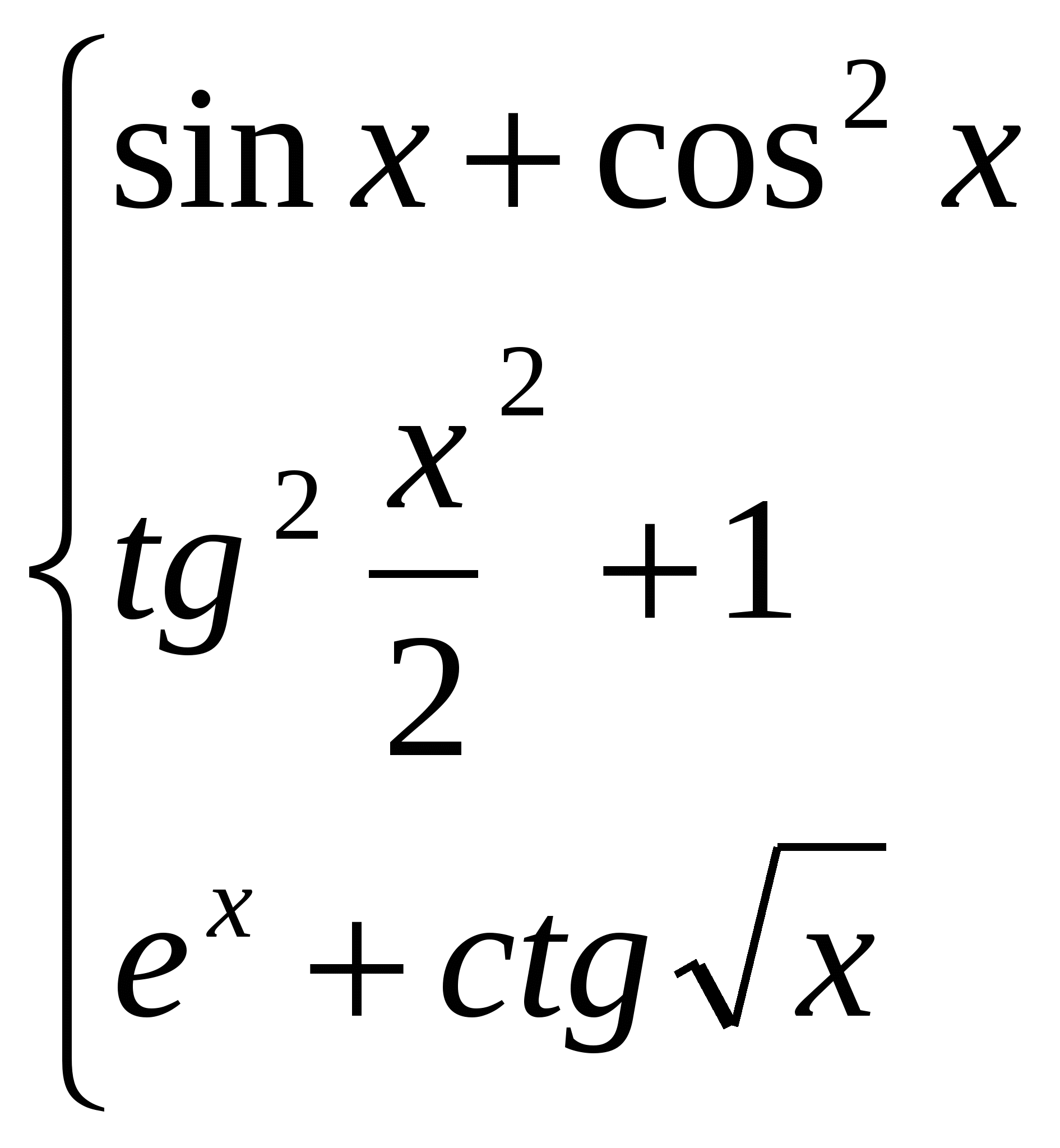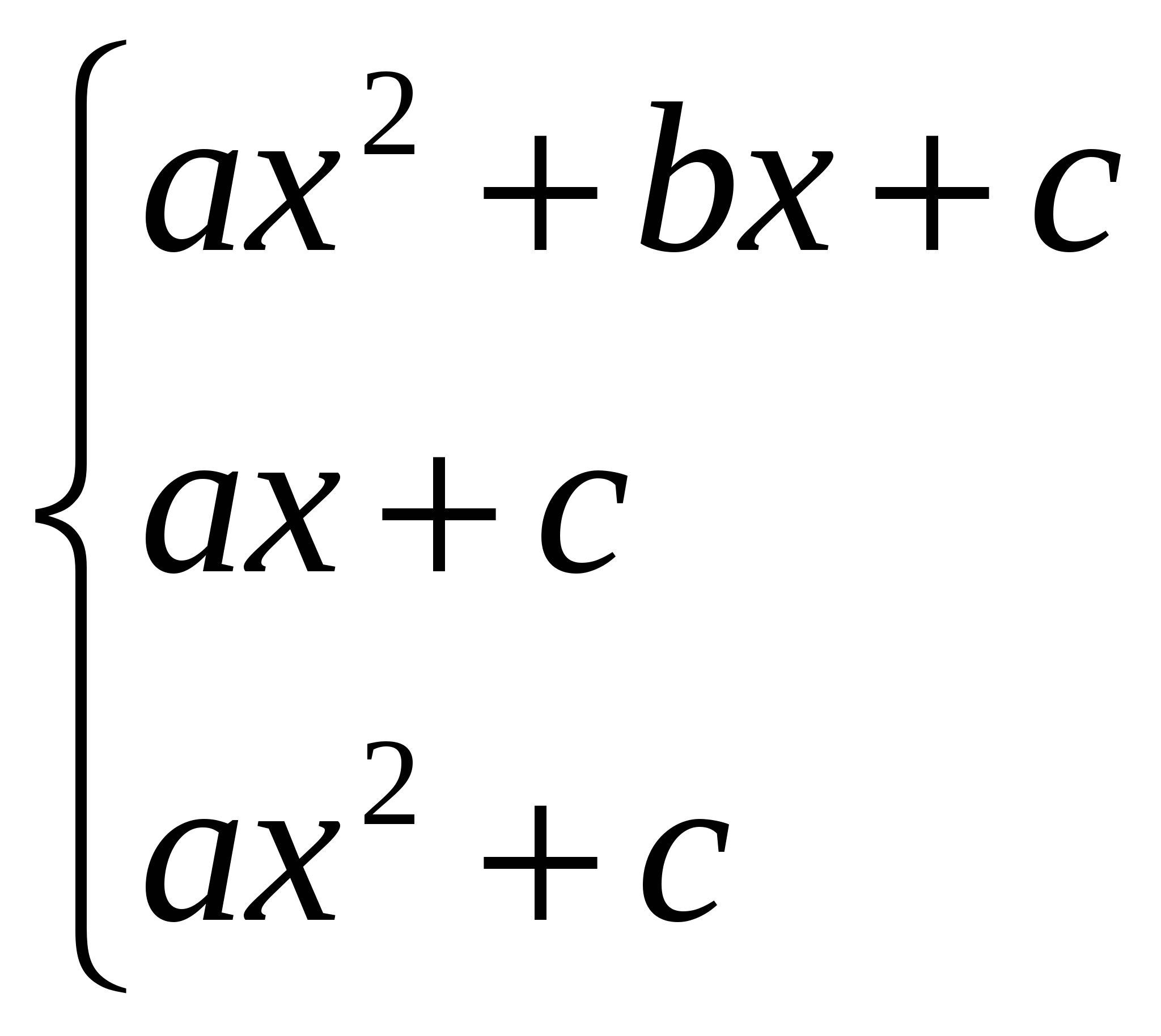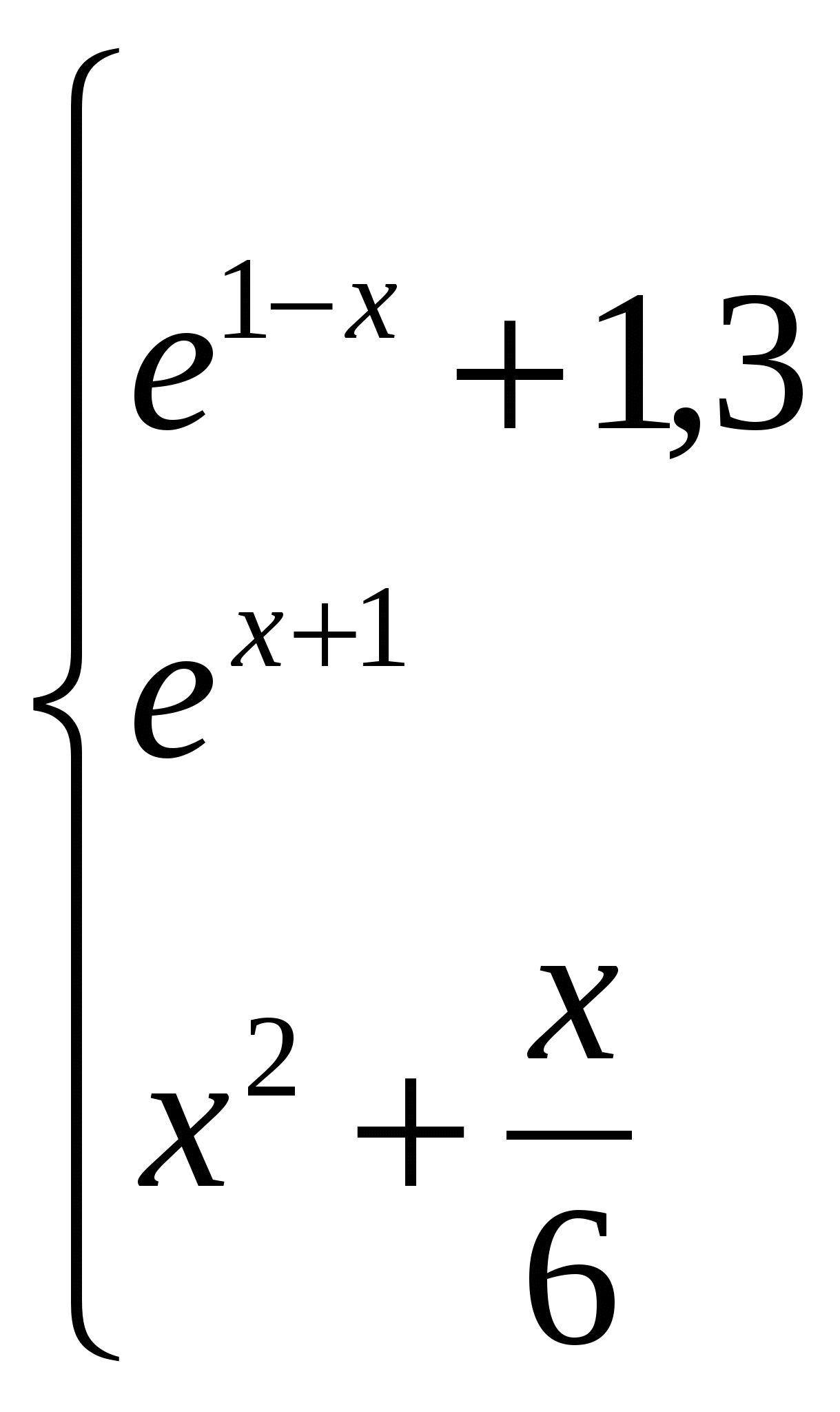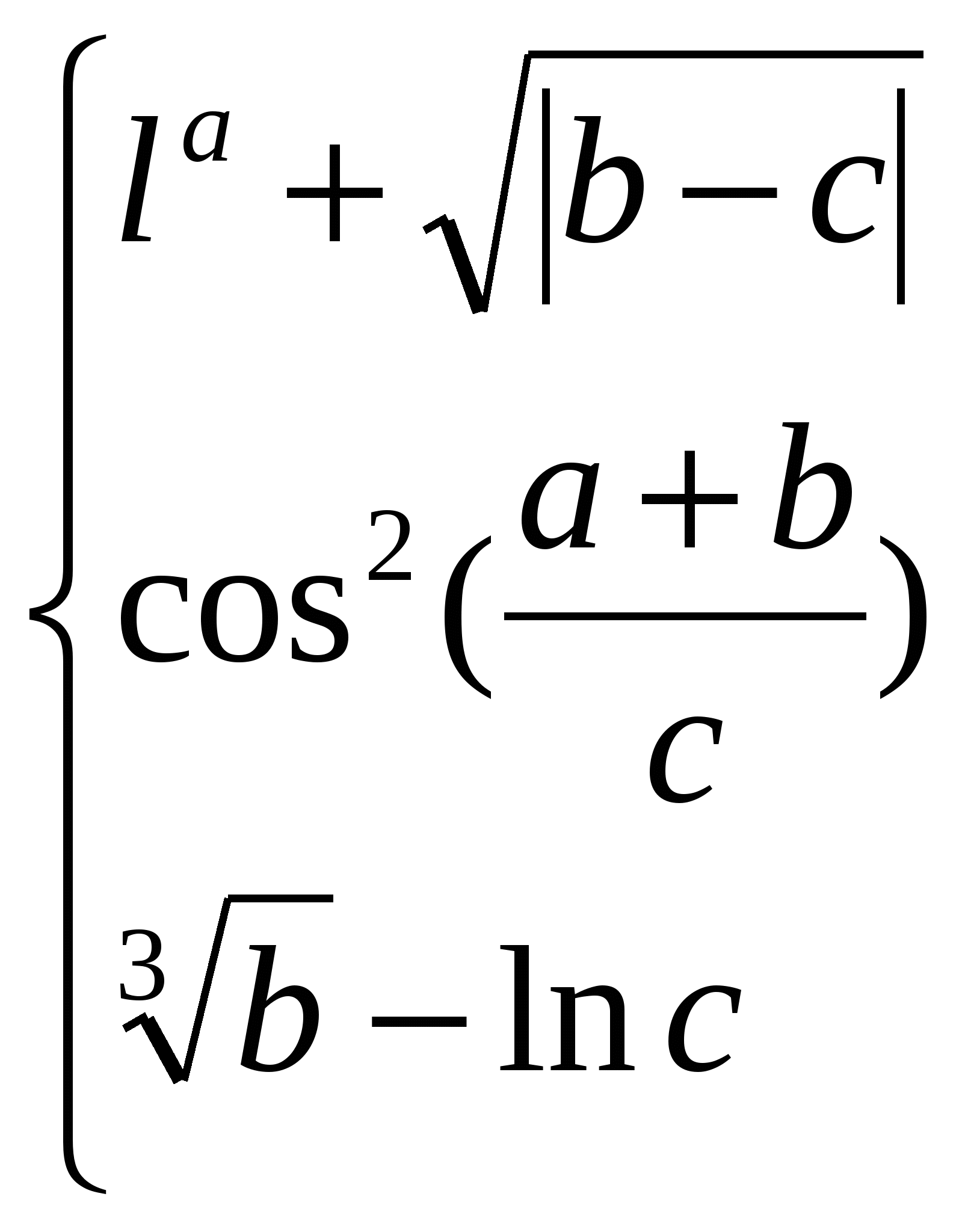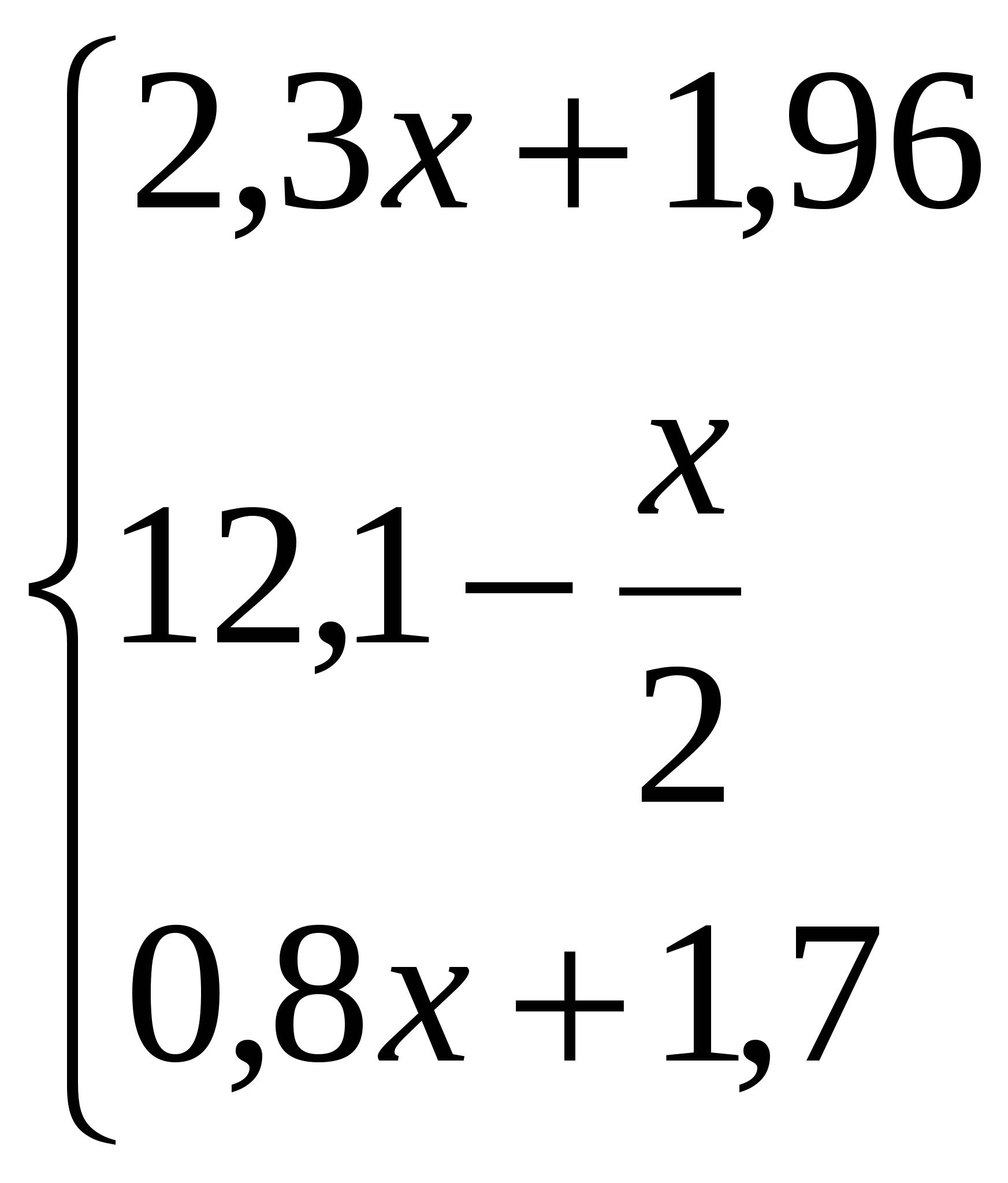Варіанти індивідуальних завдань для виконання другої частини лабораторної роботи
Обчислити T = 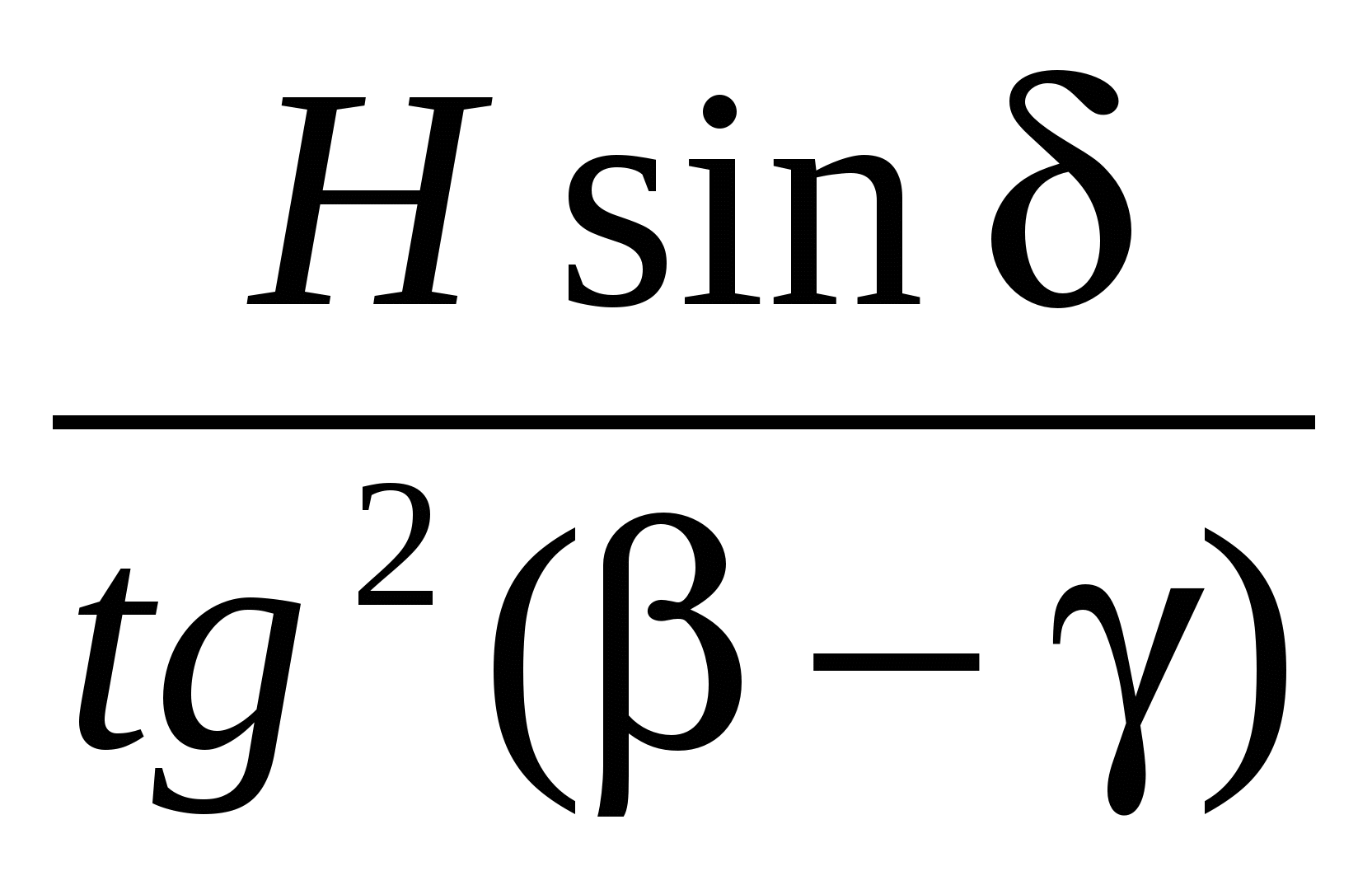 ; n = a (c g) d, ; n = a (c g) d,
де H = 1,8; = 0,01; = 0,6; = 0,03; g - FALSE; a,c,d - TRUE.
Обчислити = ctg(x)e -x ; r = z (ab-c)b+d 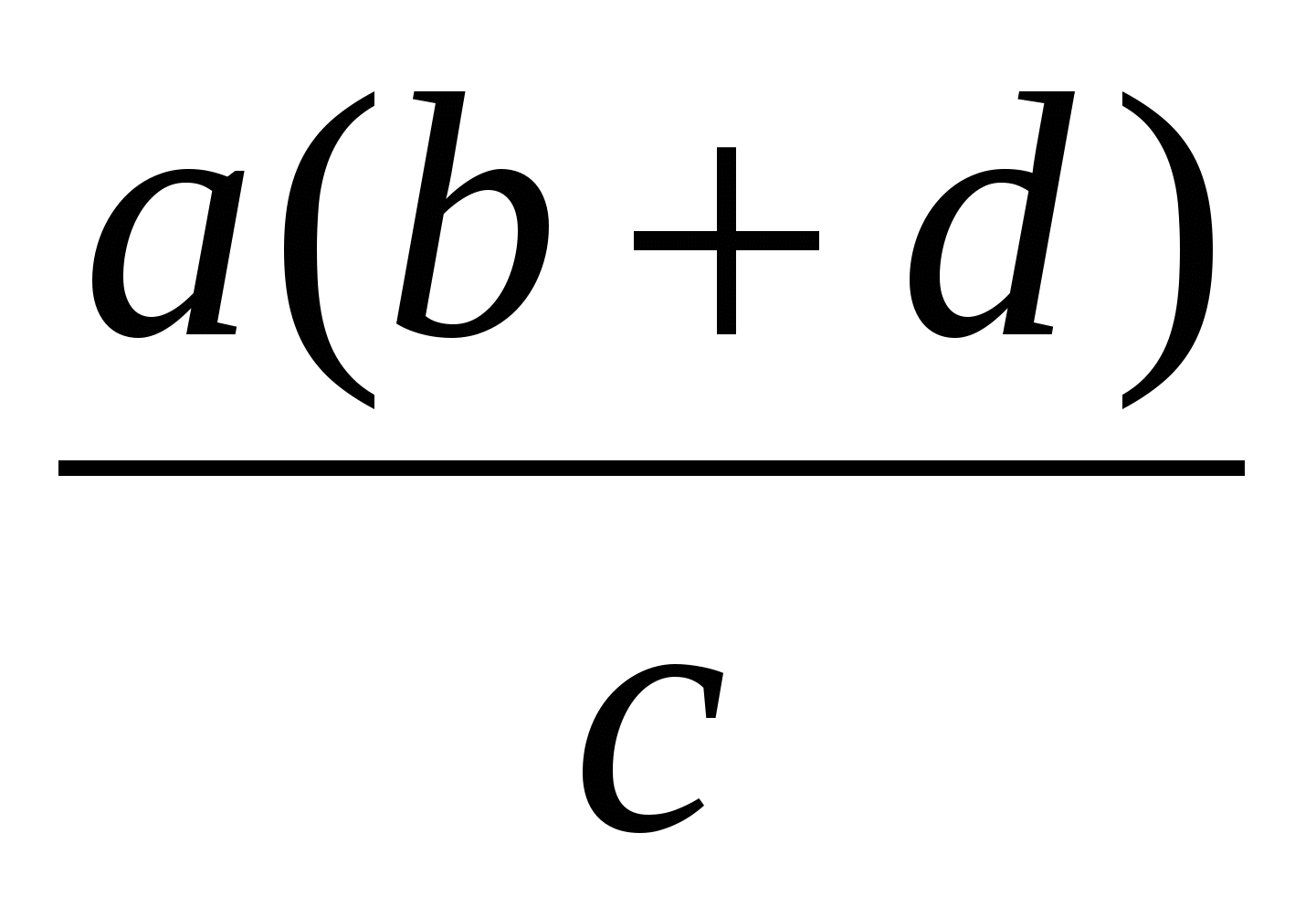 z, z,
де x = 0,47; = 1,3; a = 0,04; b = 9,3; c = 1,3; d = 12,4; z - FALSE.
Обчислити b = arctg(z) + e-(d+3); k = (5-2a) (-2) x y (x y),
де d = 1,03, z = 0,88, a = 1,003, x - TRUE, y - FALSE.
Обчислити m = 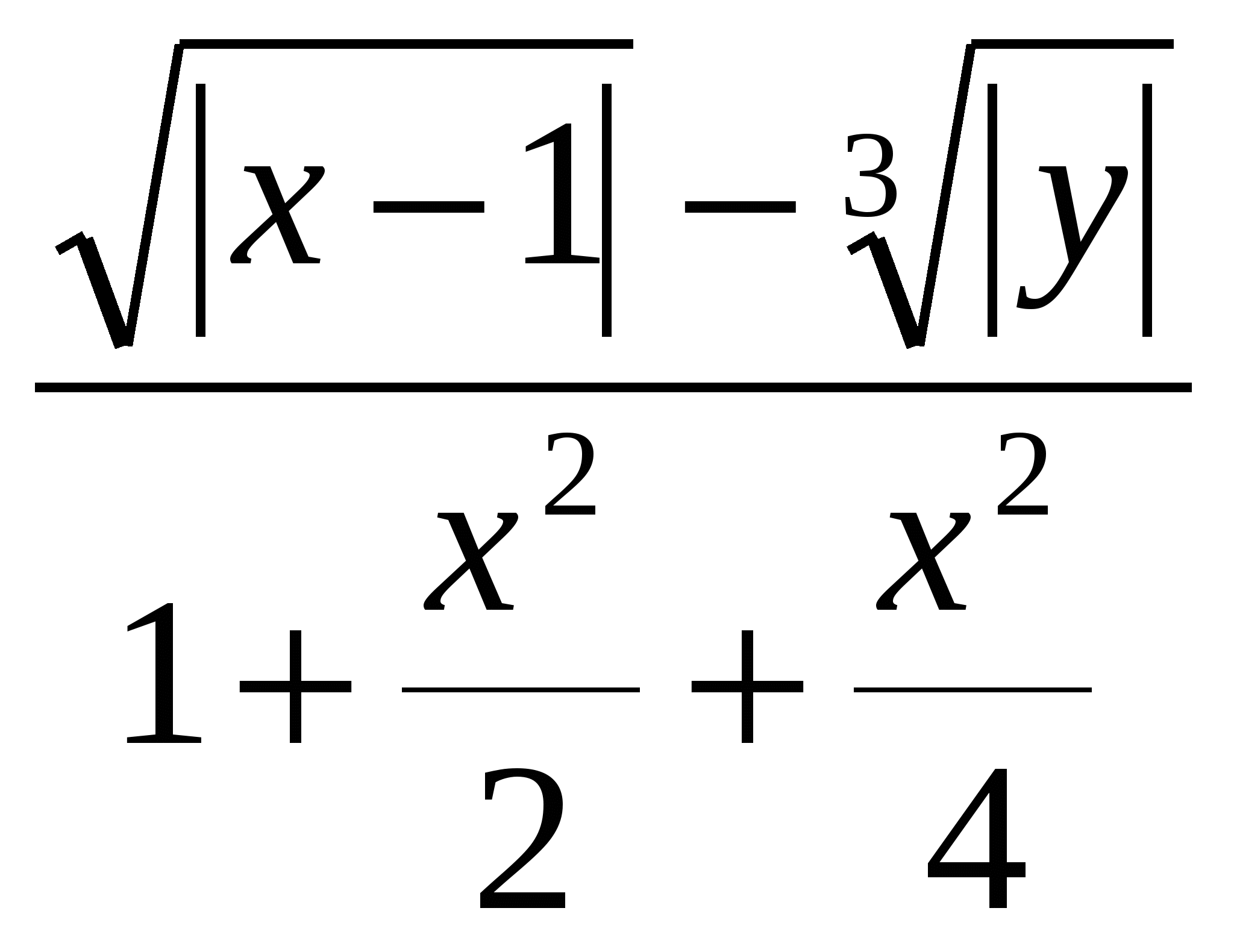 ; ;
d = 3,47 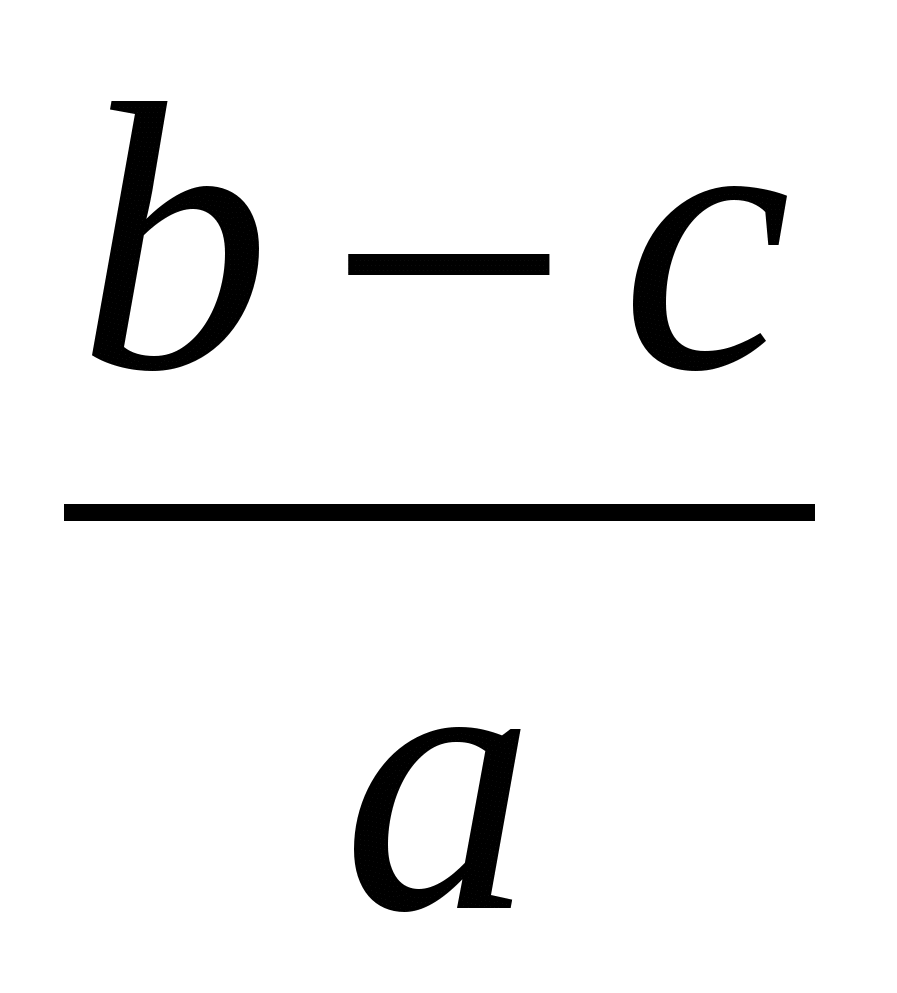 +b (a-8,9c) ((c-a) 3b) r, +b (a-8,9c) ((c-a) 3b) r,
де x = 0,4; y = 0,69; c = 1,64; b = 2,03; a = 2,61; r - TRUE.
Обчислити u = 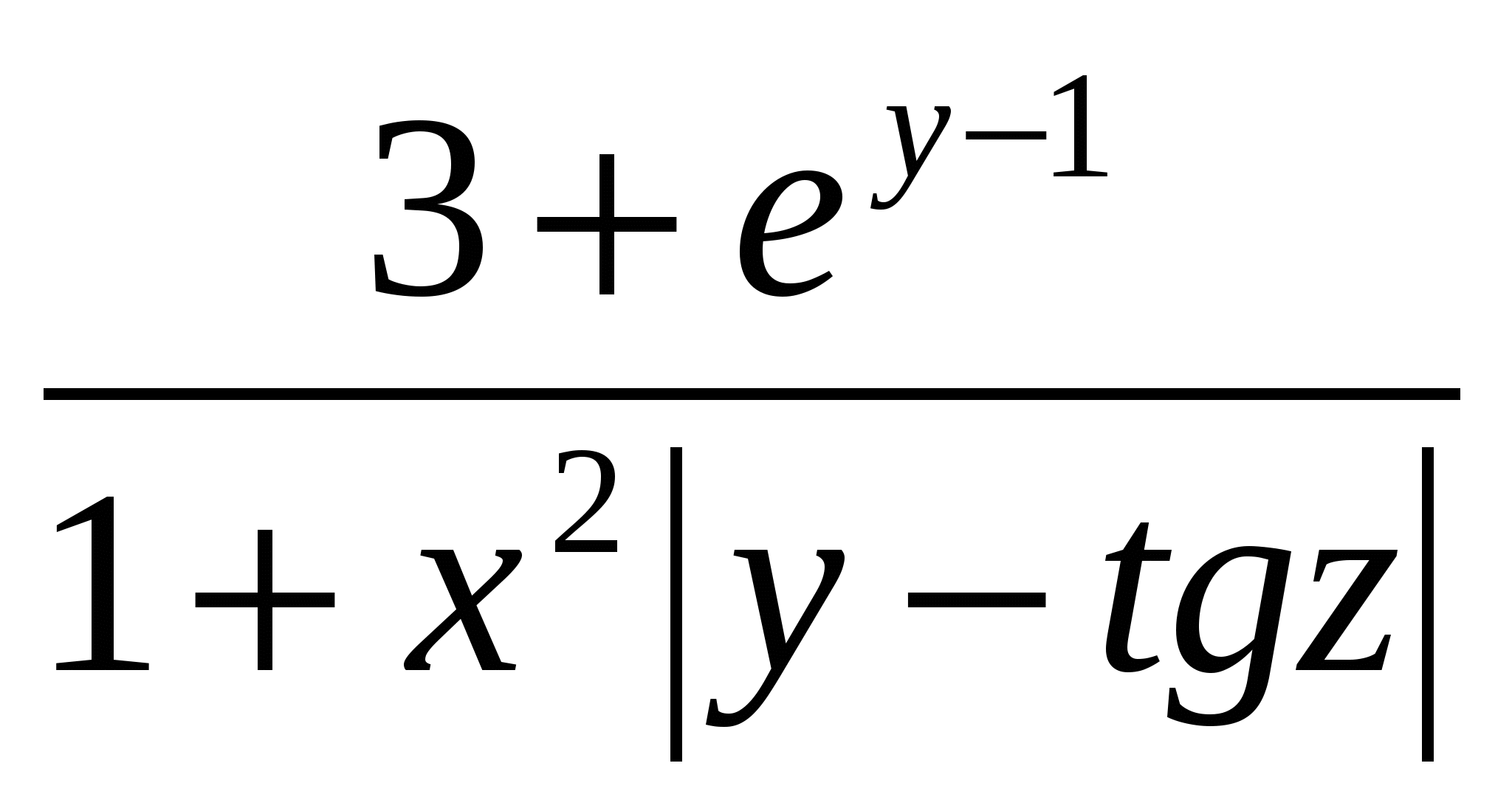 ; b = (x1 y1 z1) (a log2 c), ; b = (x1 y1 z1) (a log2 c),
де y =1,49; x = 2,4; z = 0,04; a = 2,4; c = 1,64; x1,z1 - TRUE; y1 - FALSE.
Обчислити 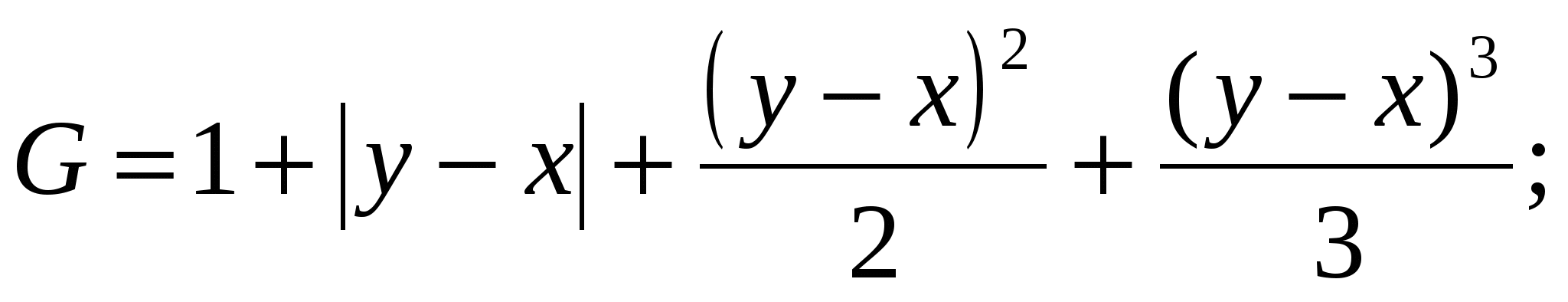
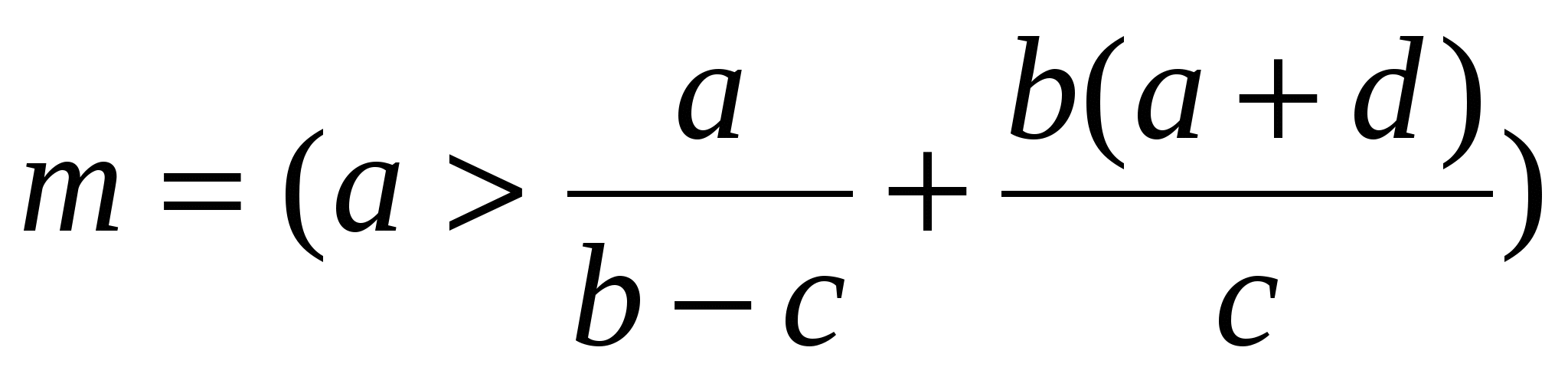 ((0,6a+0,3b)2 ((0,6a+0,3b)2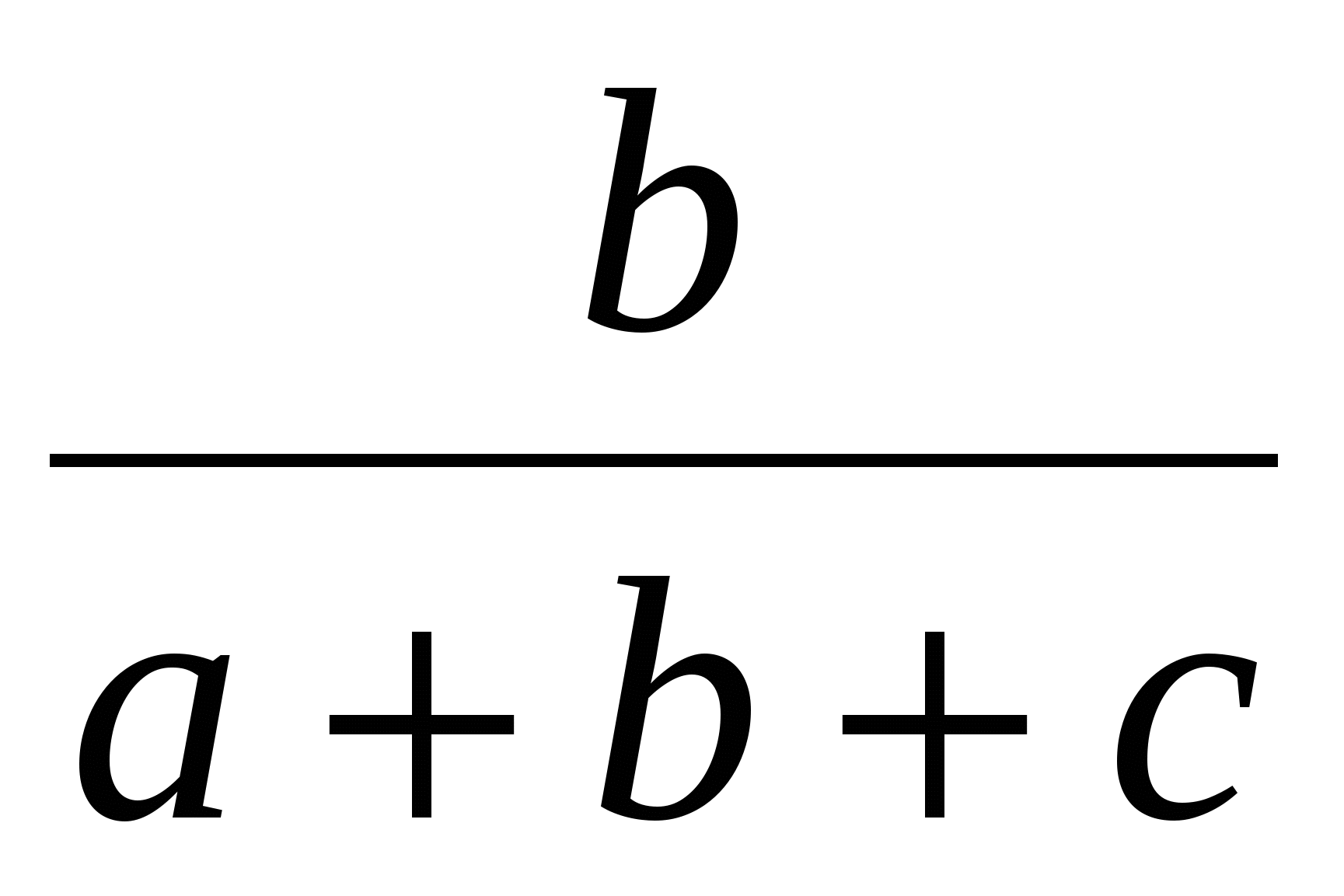 n, n,
де y = 1,45; x = 1,64; a = 3,344; b = 1,08; c = 1,002; d = 0,33; n - TRUE.
Обчислити 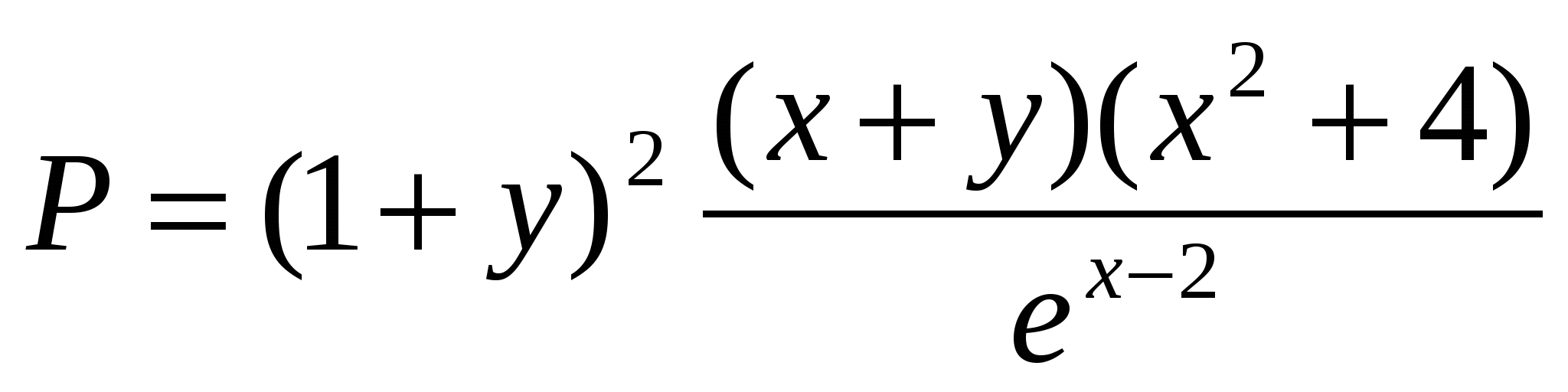 ; ;
b=( a (b c) d) ((x+y) 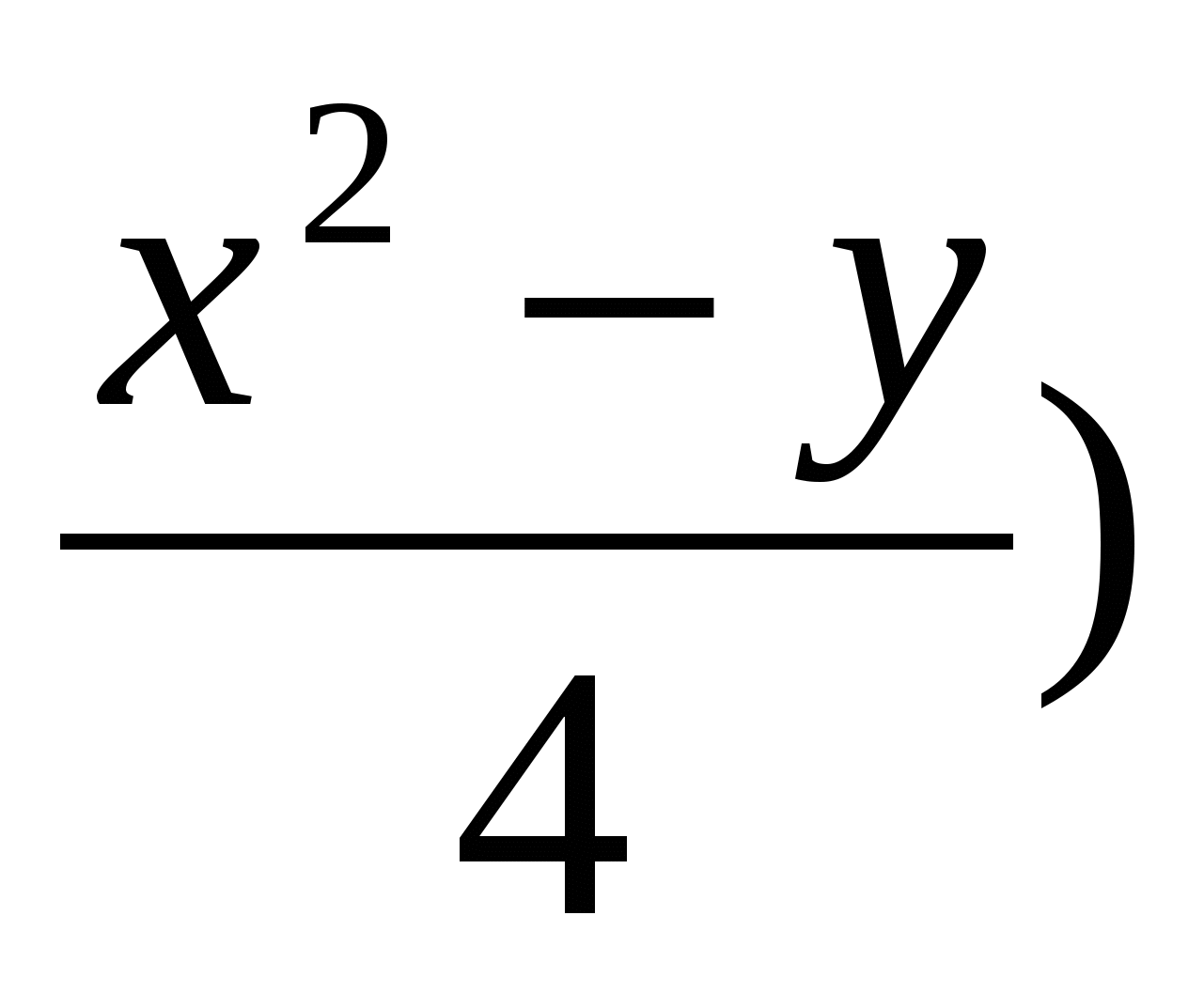 , ,
де y = 1,55; x = 2,07; a,c - TRUE; b,d - FALSE.
Обчислити 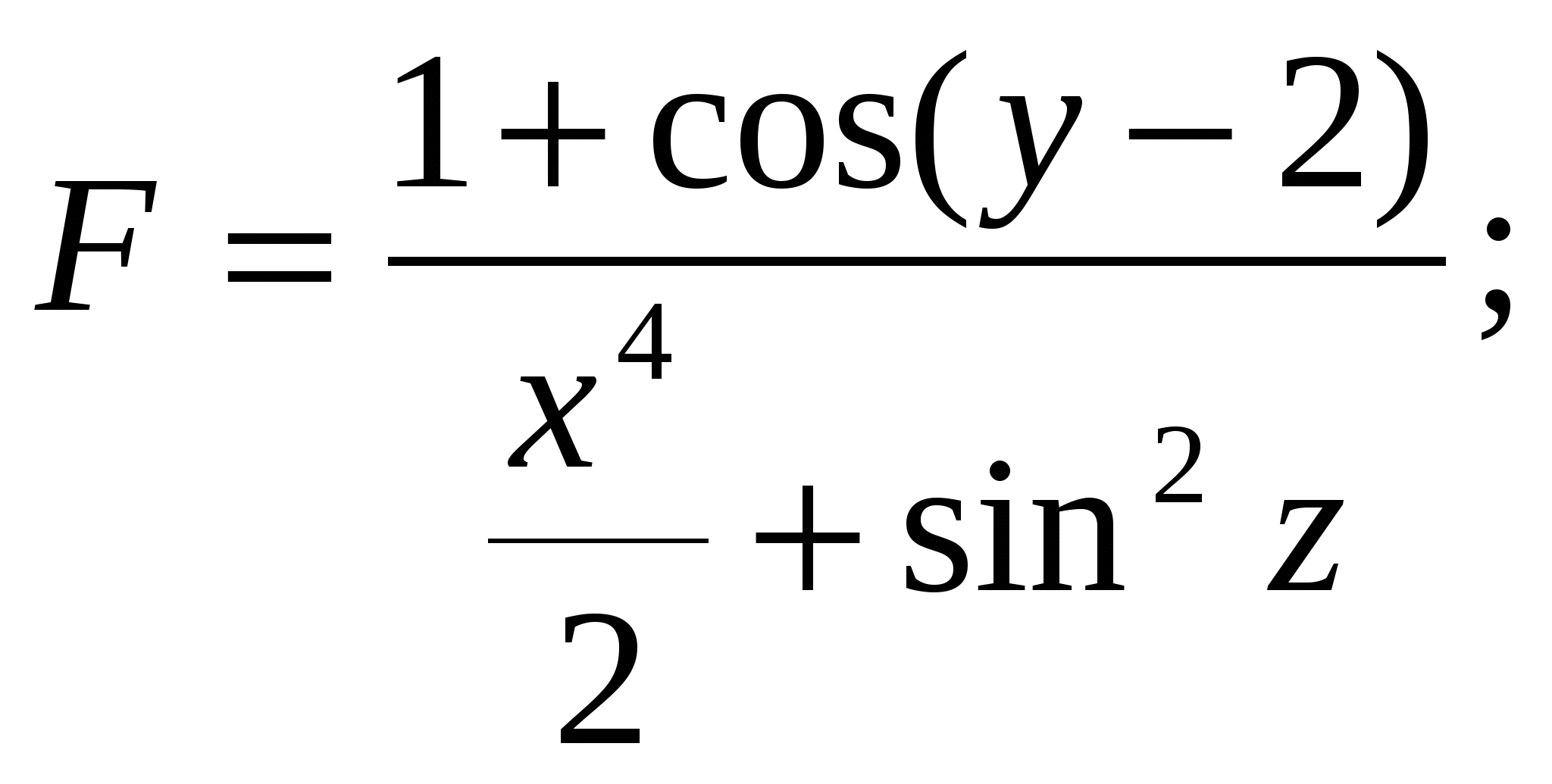 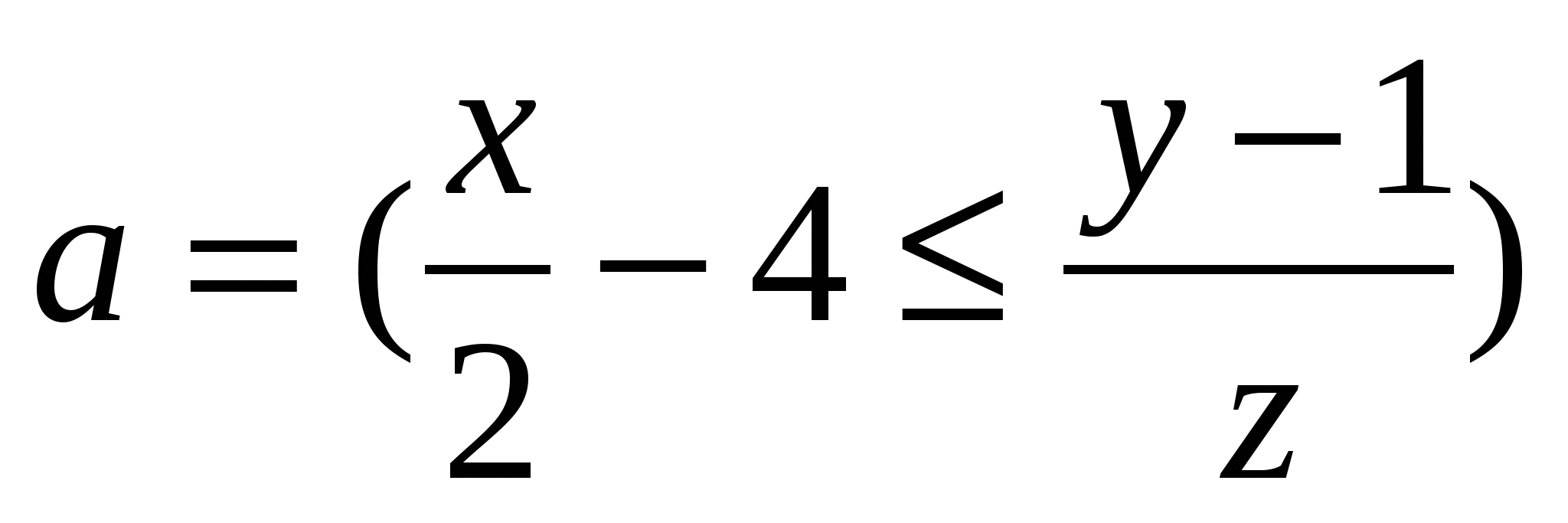 ( b ( d c)), ( b ( d c)),
де y = 2,04; x = 3,12; z = 0,813; d - TRUE; b, c - FALSE.
Обчислити 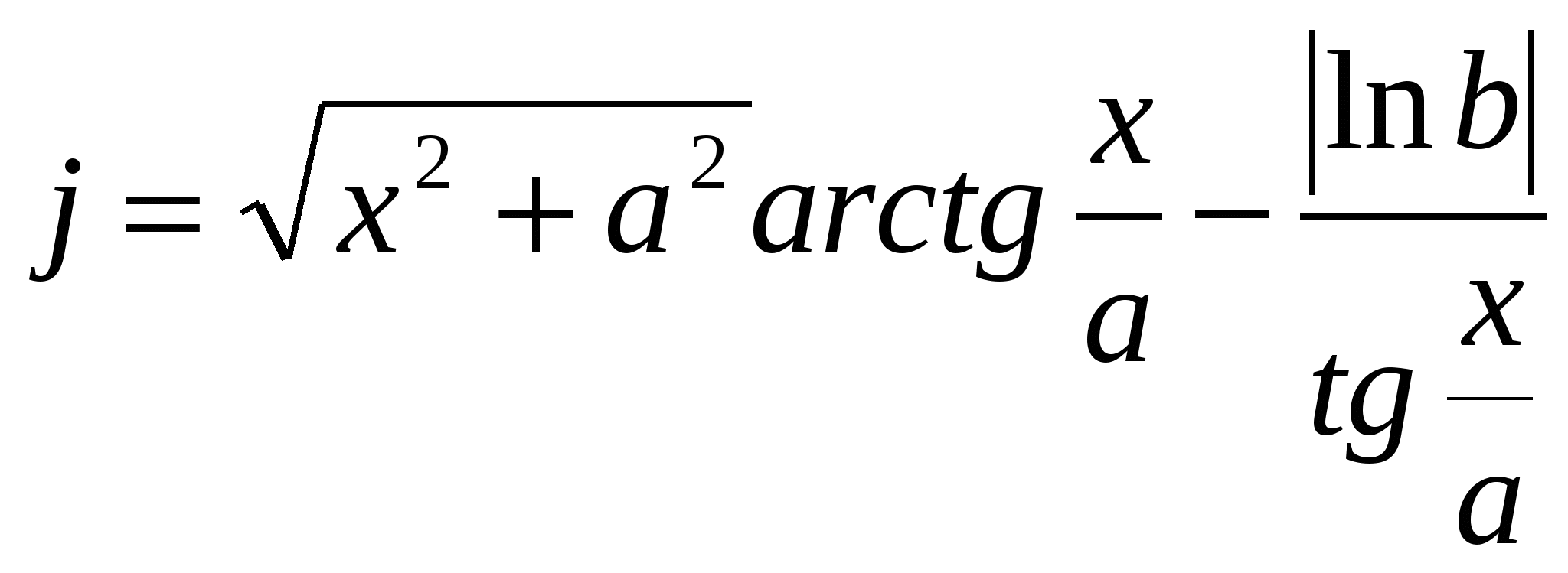 ; z=(sin2a+cos 2b ln x - tg y) d, ; z=(sin2a+cos 2b ln x - tg y) d,
де y = 1,49; x = 1,45; b = 2,27; a = 0,31; d - FALSE.
Обчислити 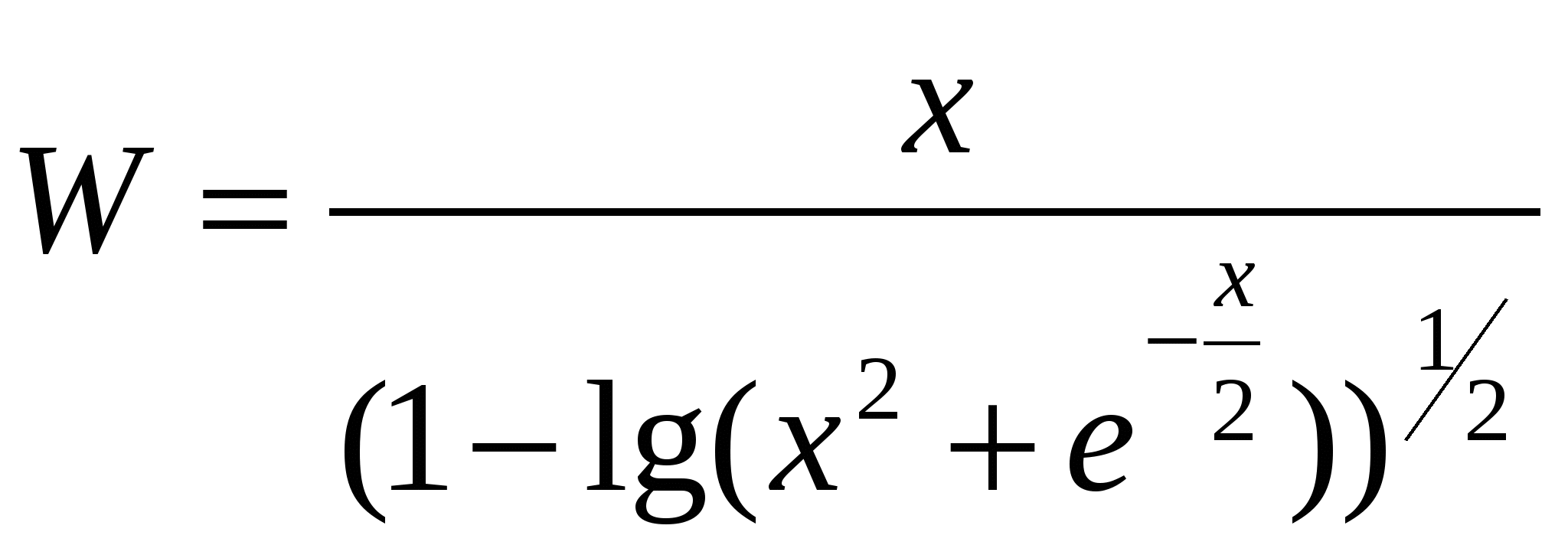 ; ; 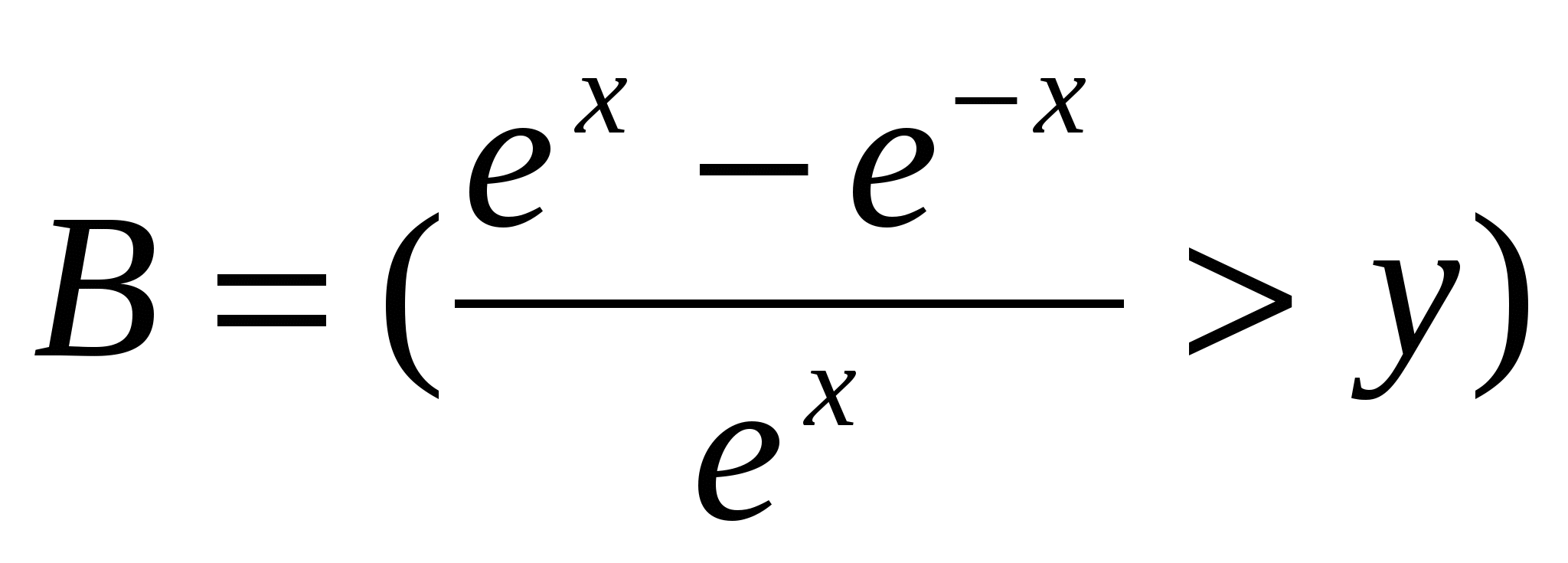 (arctg 80 3z), (arctg 80 3z),
де y = 1,12; x = 2,443; z = 1,39.
Обчислити 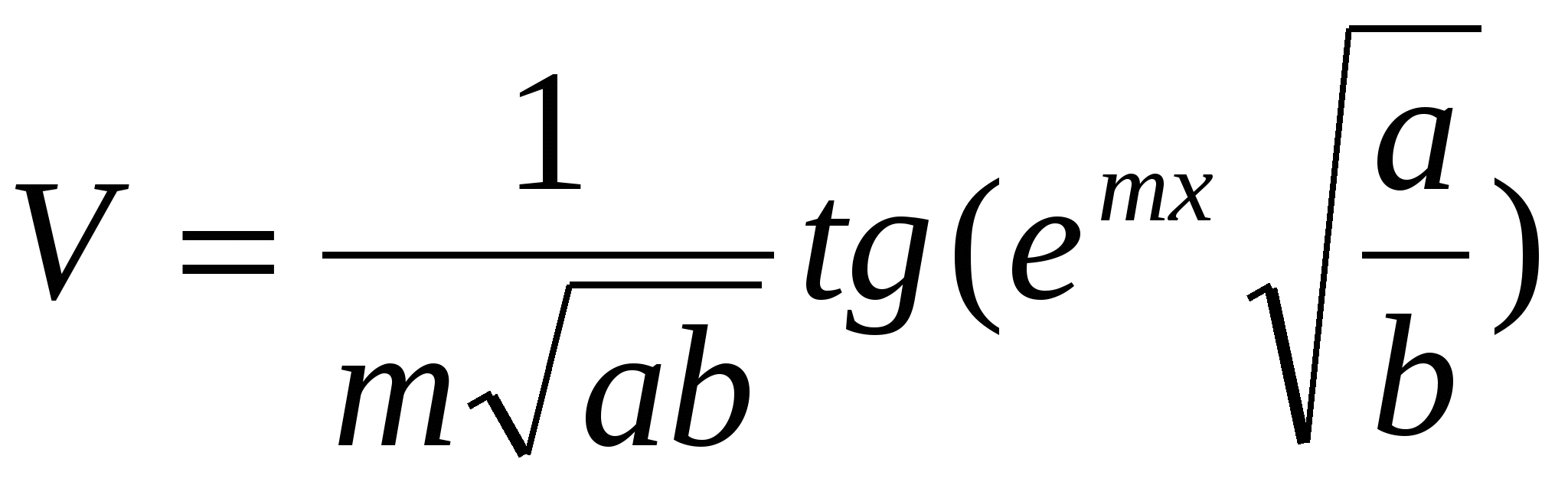 ; D=(1,4a b) (d c), ; D=(1,4a b) (d c),
де m = 1,14; x = 1,45; a = 2,64; b = 1,93; c - TRUE; d - FALSE.
Обчислити 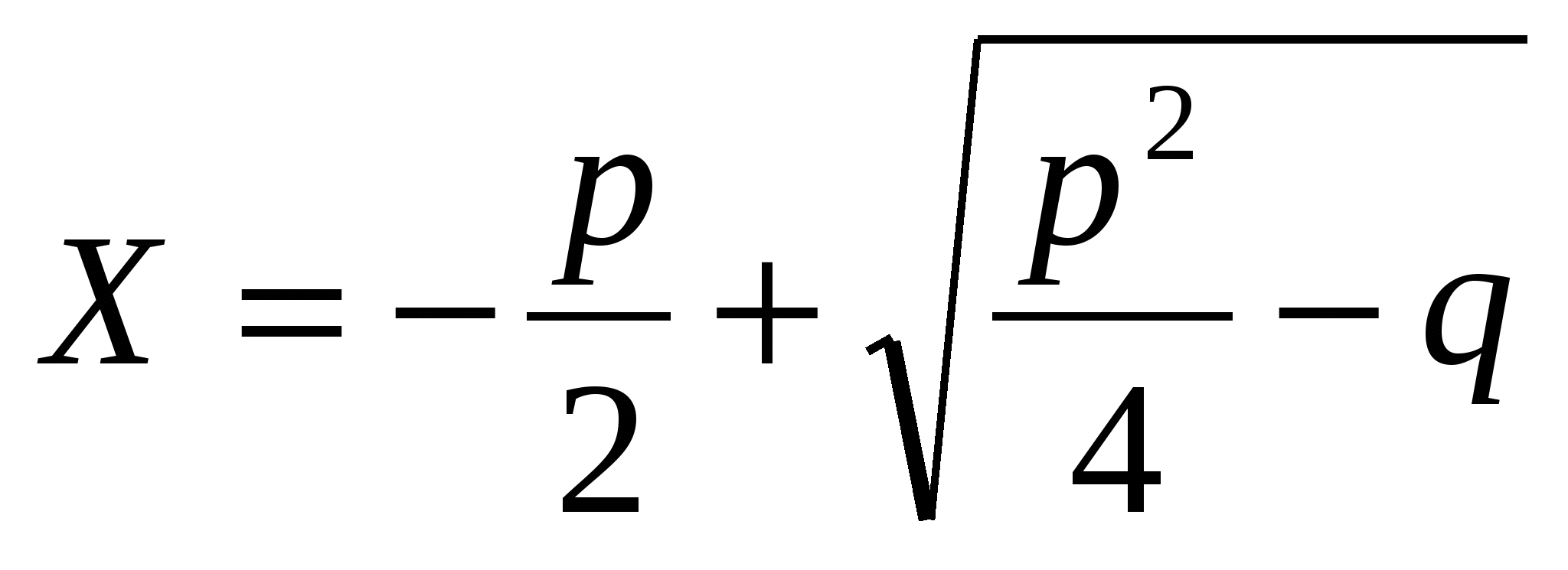 ; ; 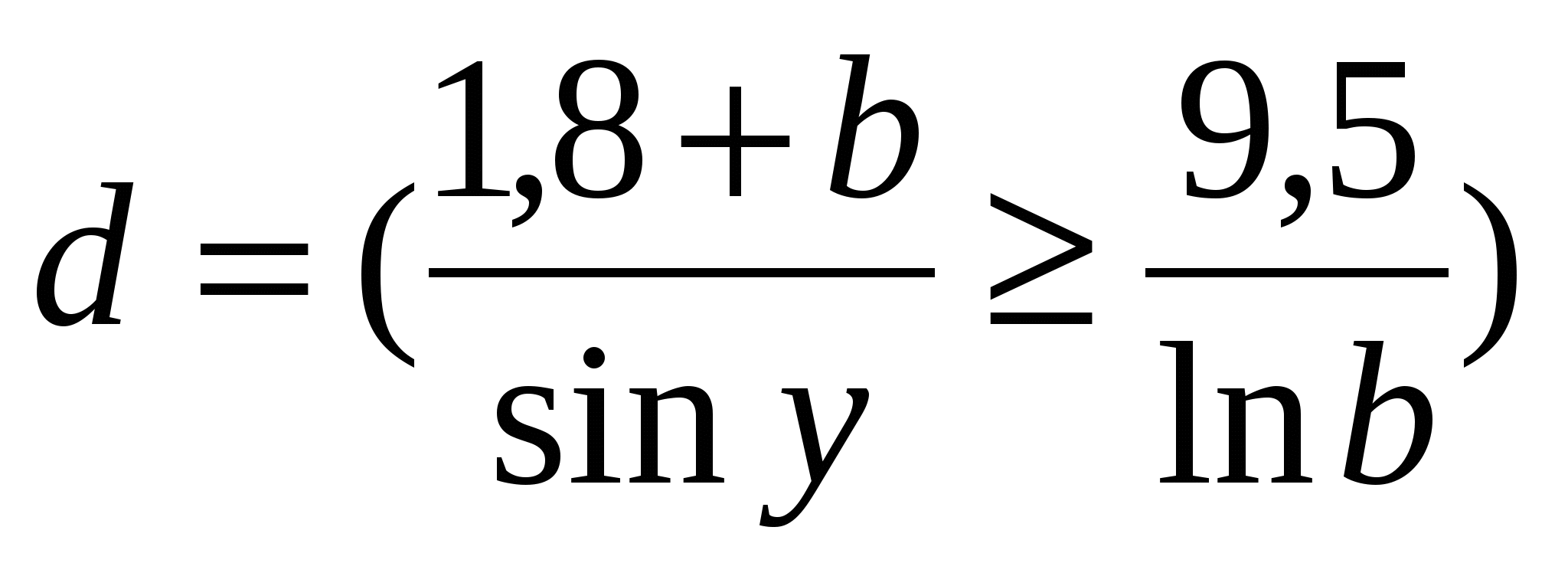 r a c, r a c,
де p = 5,61; q = 3,156; b = 3,3; y = 0,69; r,c - TRUE; a - FALSE.
Обчислити 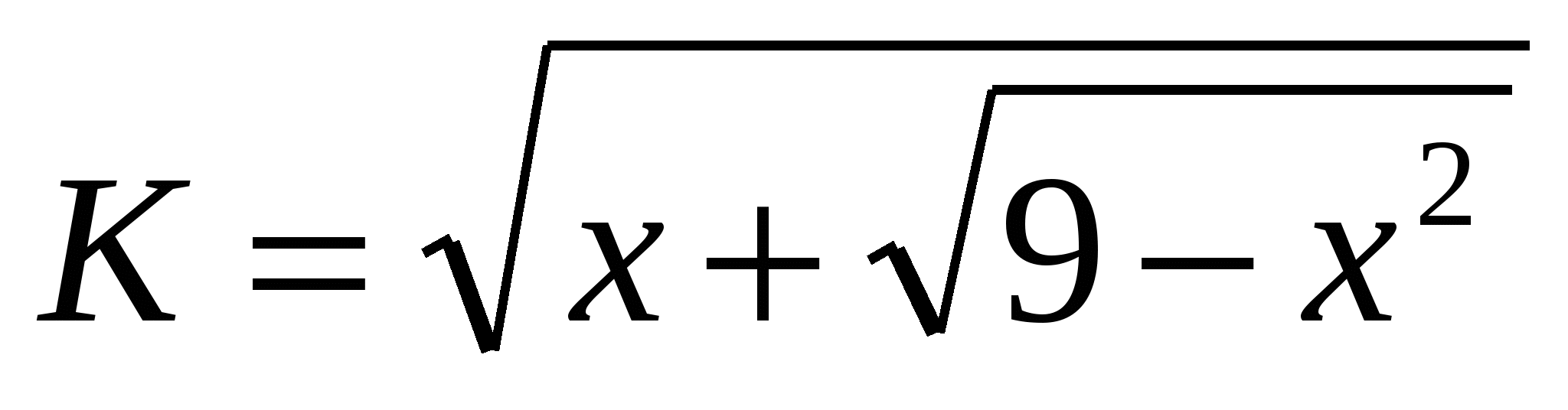 ; ;
a= ( b c ) d q (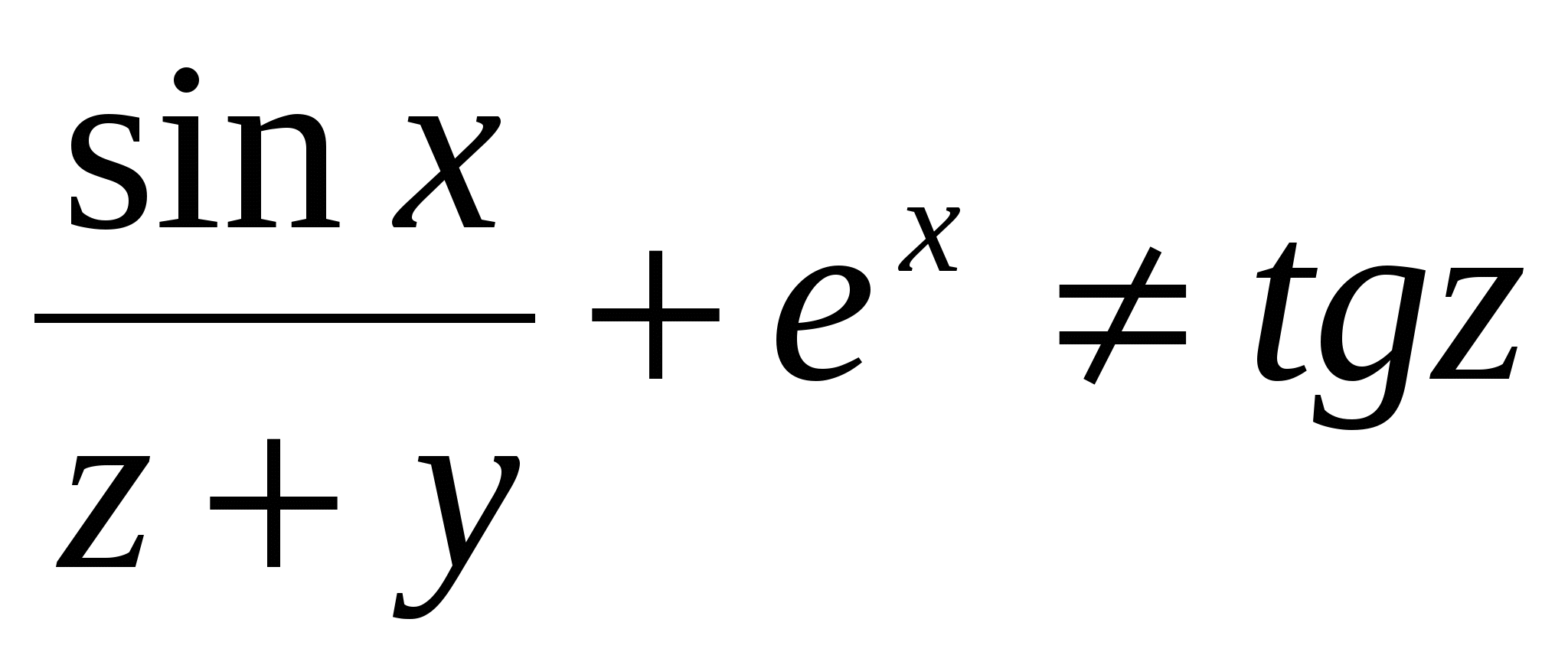 ), ),
де y = 1,92; x = 2,346; z = 2,03; b,d,q - TRUE; c - FALSE.
Обчислити 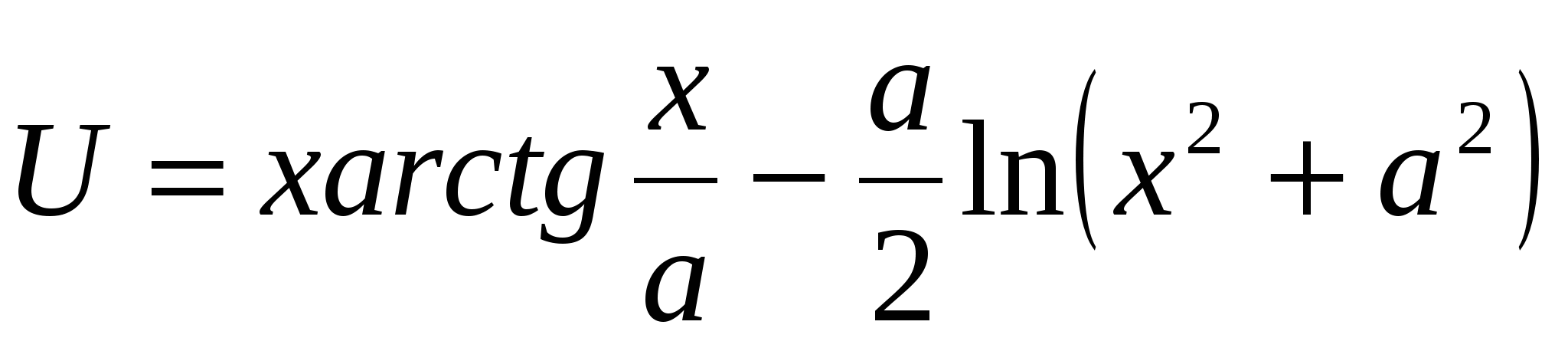 ; ;
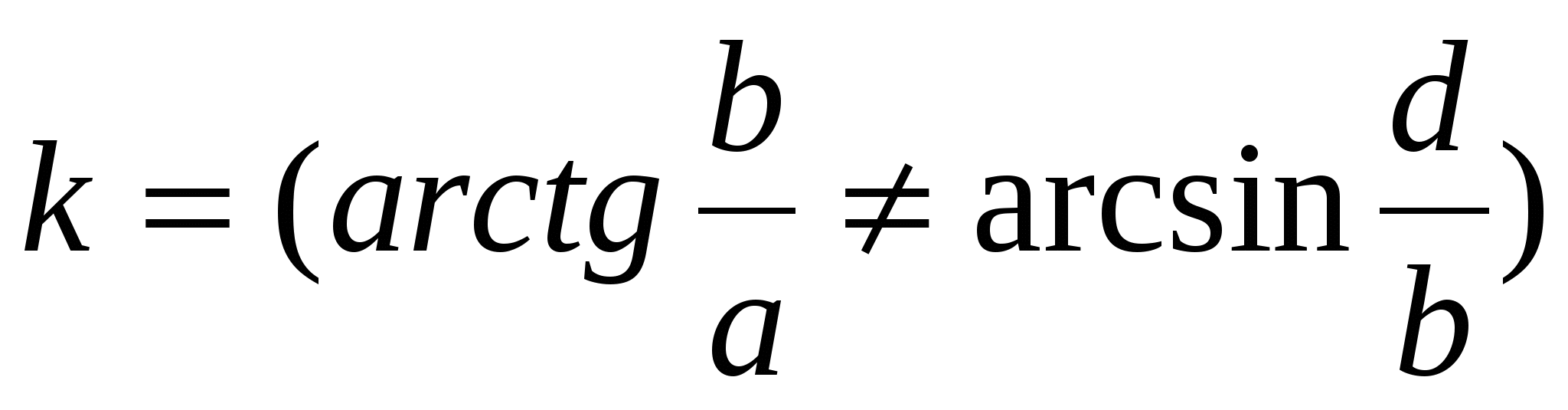 ( ( (c p))), ( ( (c p))),
де d =0,64; x = 1,41; a = 2,13; b = 1,02; c - TRUE; p- FALSE.
Обчислити 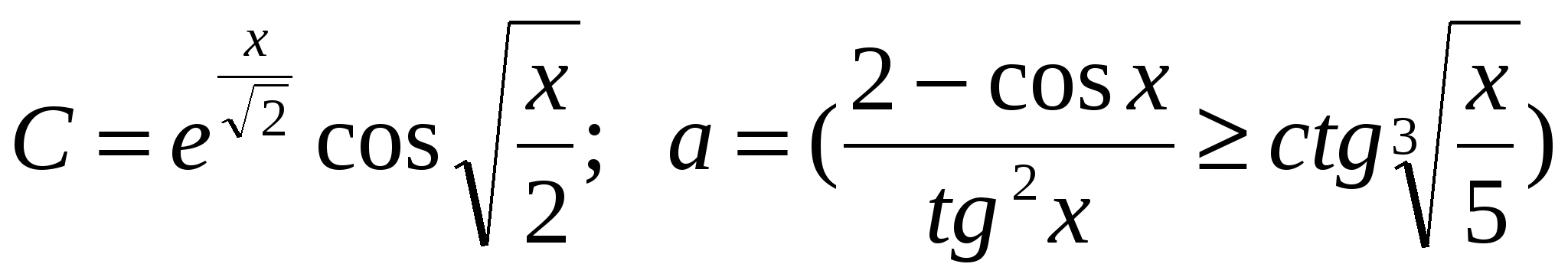 (m n) m, (m n) m,
де x = 1,333; m - TRUE; n - FALSE.
Обчислити 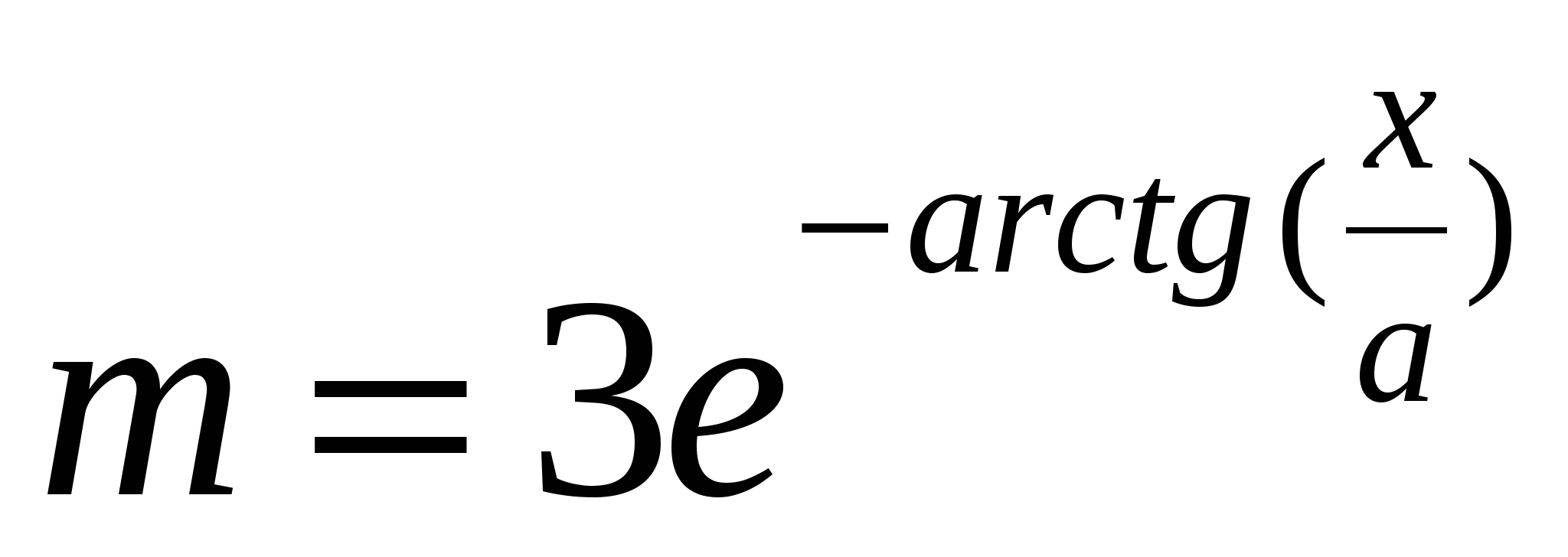 ; b= ( y ( y z ) ; b= ( y ( y z ) 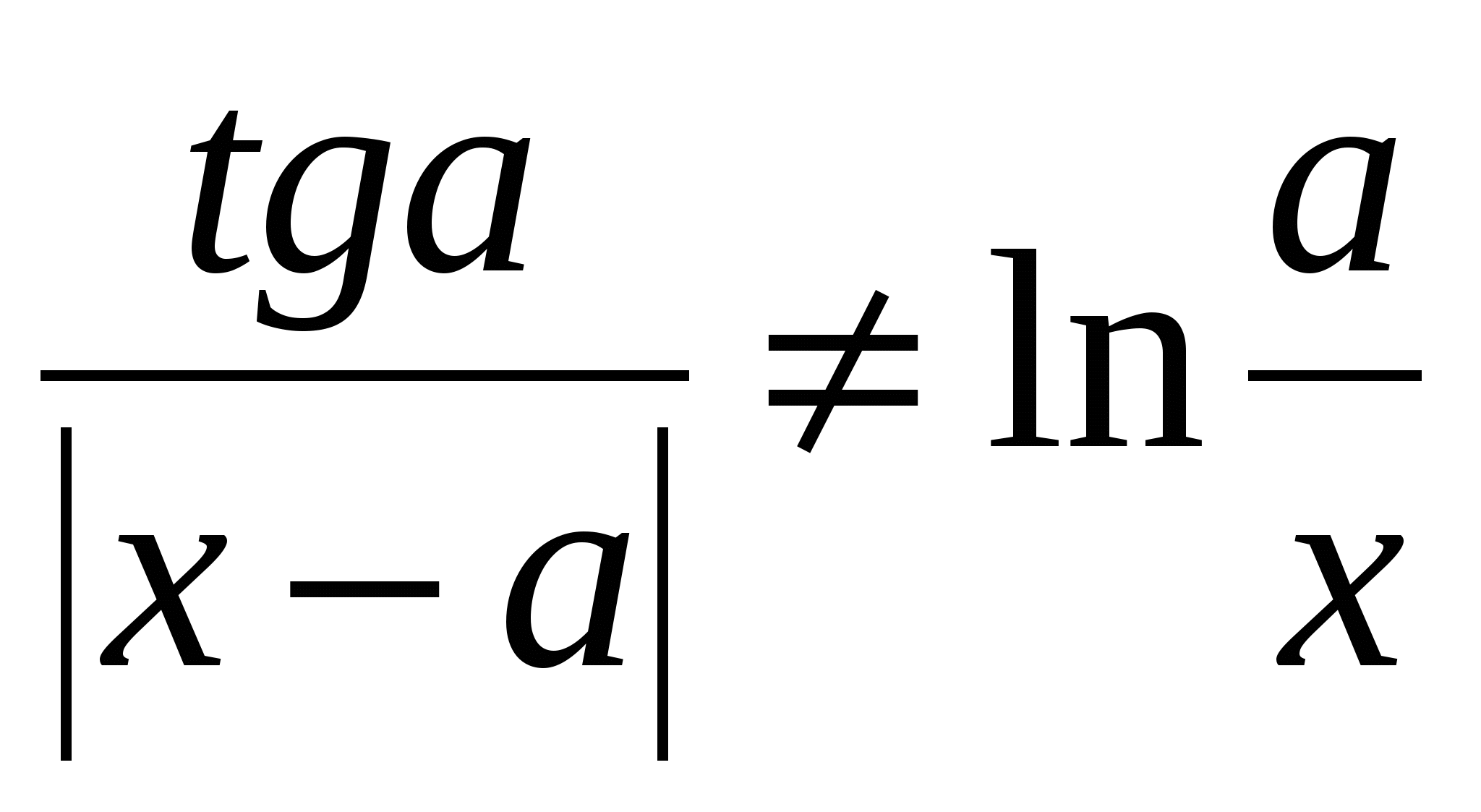 ), ),
де x = 0,627; a = 0,599; z - TRUE; y - FALSE.
Обчислити 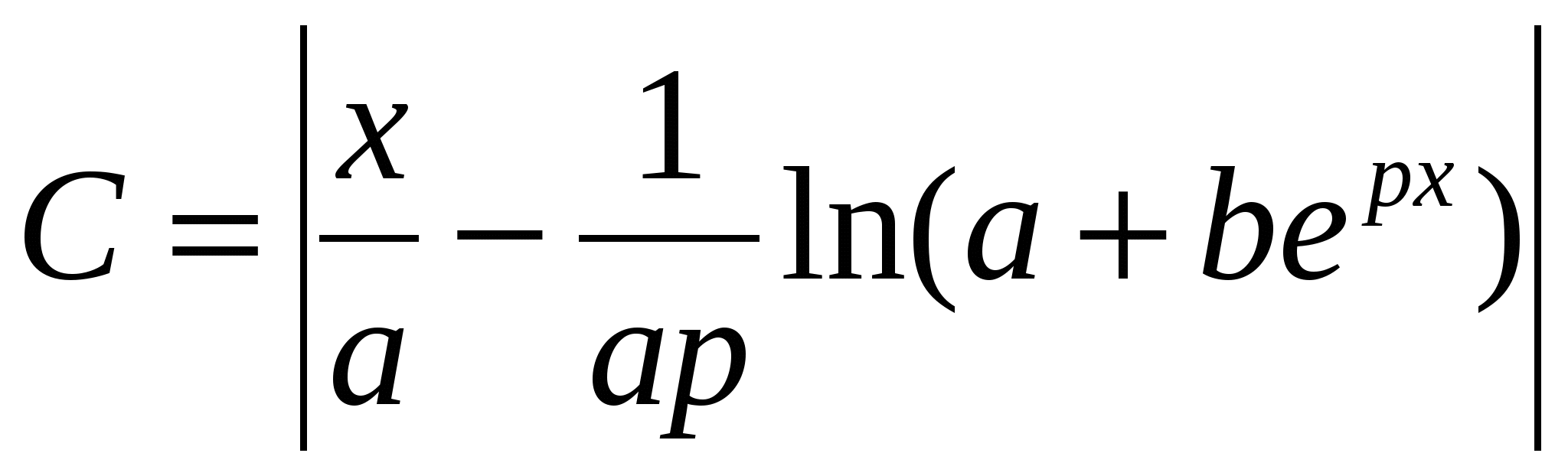 ; ; 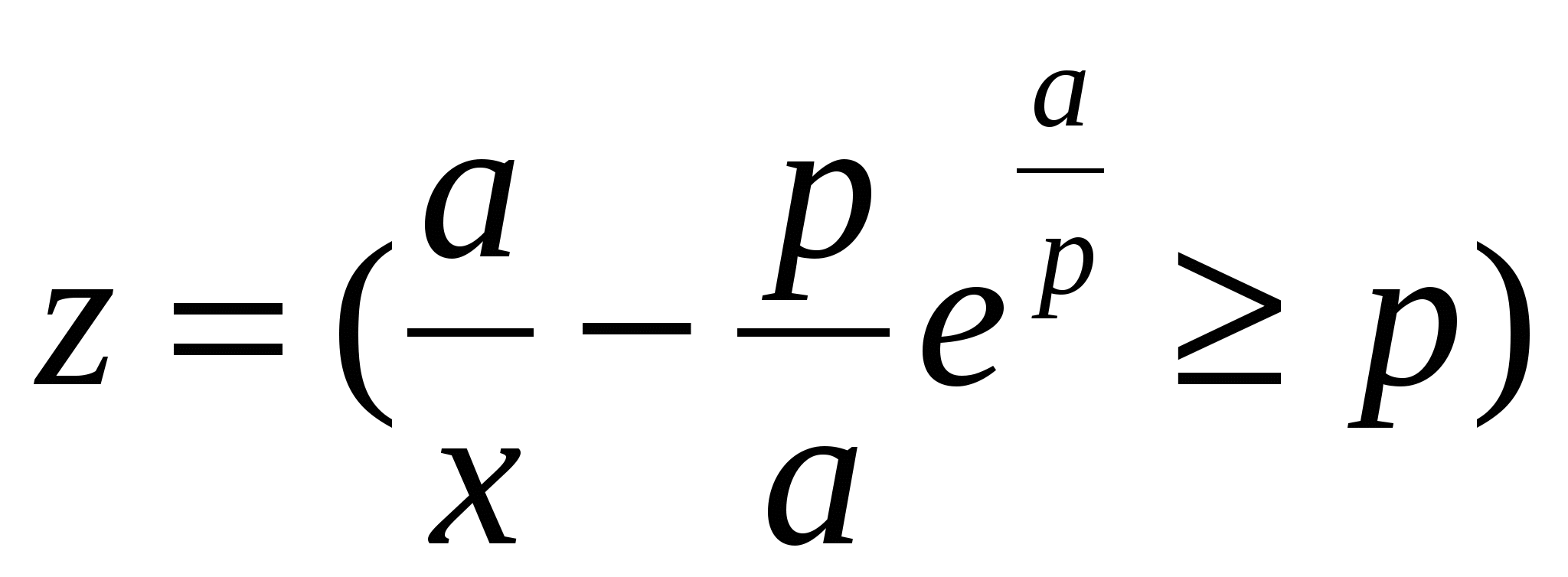 m (n m), m (n m),
де x = 1,422; a = 3,799; p = 1,04; b = 0,43; m - TRUE; n - FALSE.
Обчислити 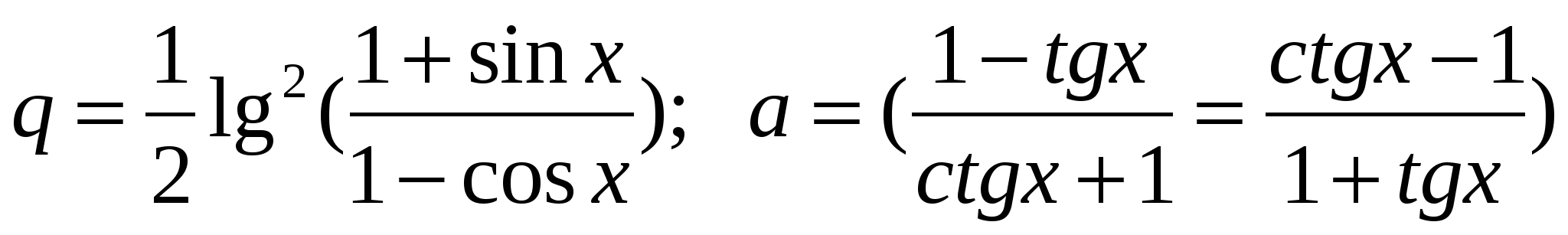 (d(bd)), (d(bd)),
де x = 0,644; d - TRUE; b - FALSE.
Обчислити 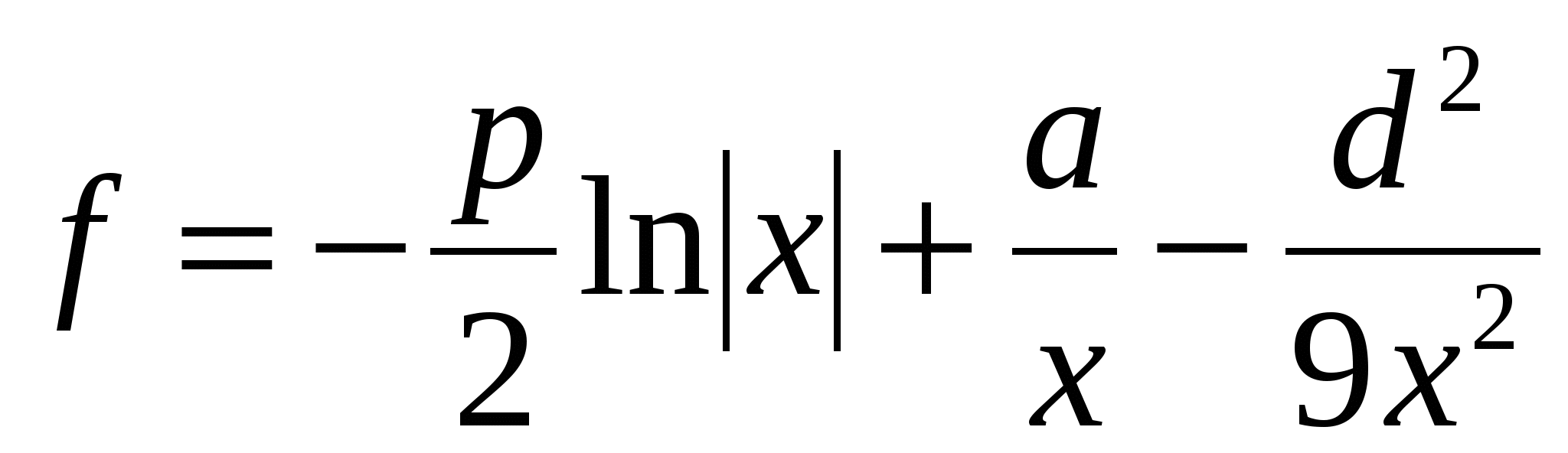 ; ; 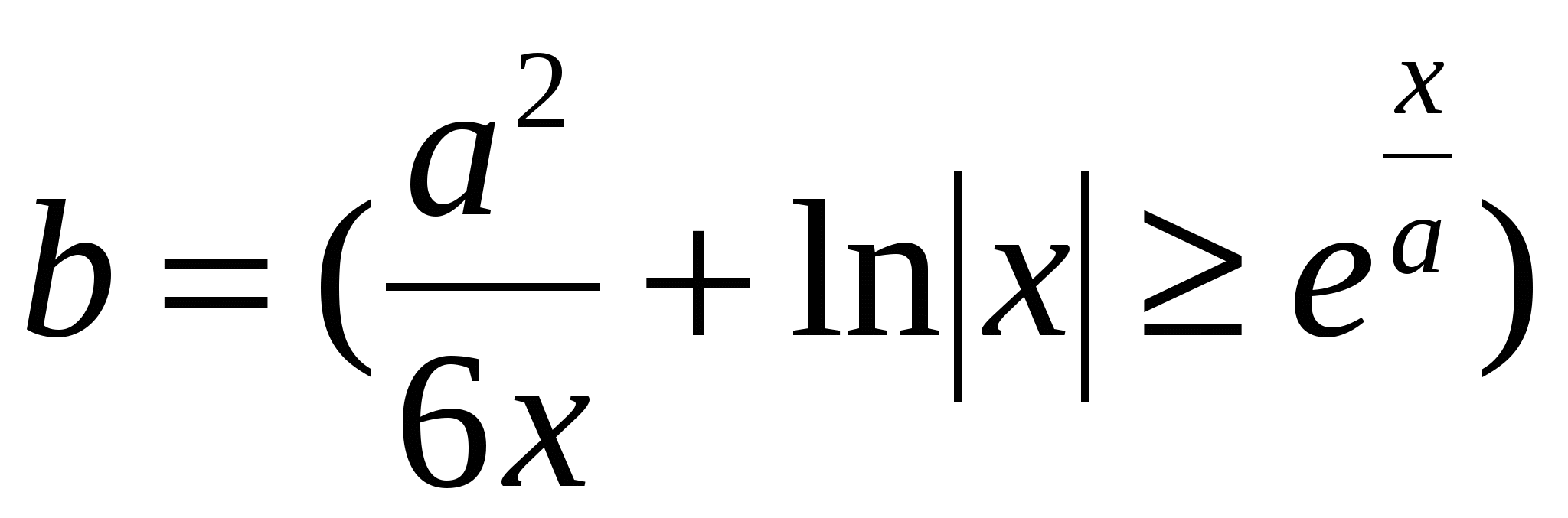 m n m n m, m n m n m,
де p = 4,33; x = 1,699; a = 2,06; n - TRUE; m - FALSE.
Обчислити 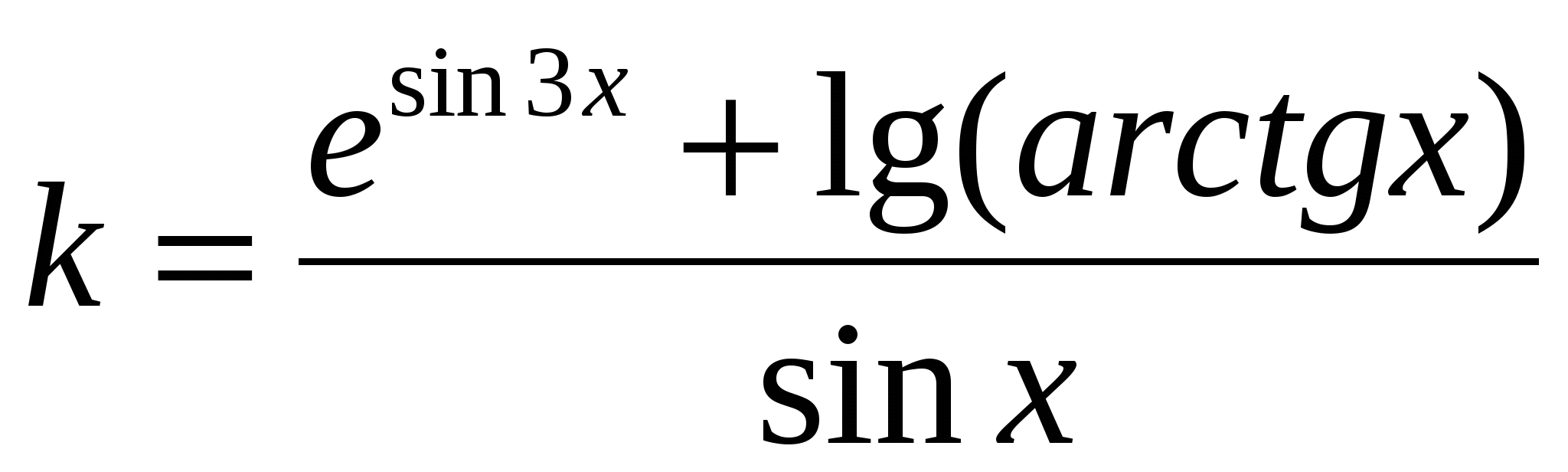 ; ; 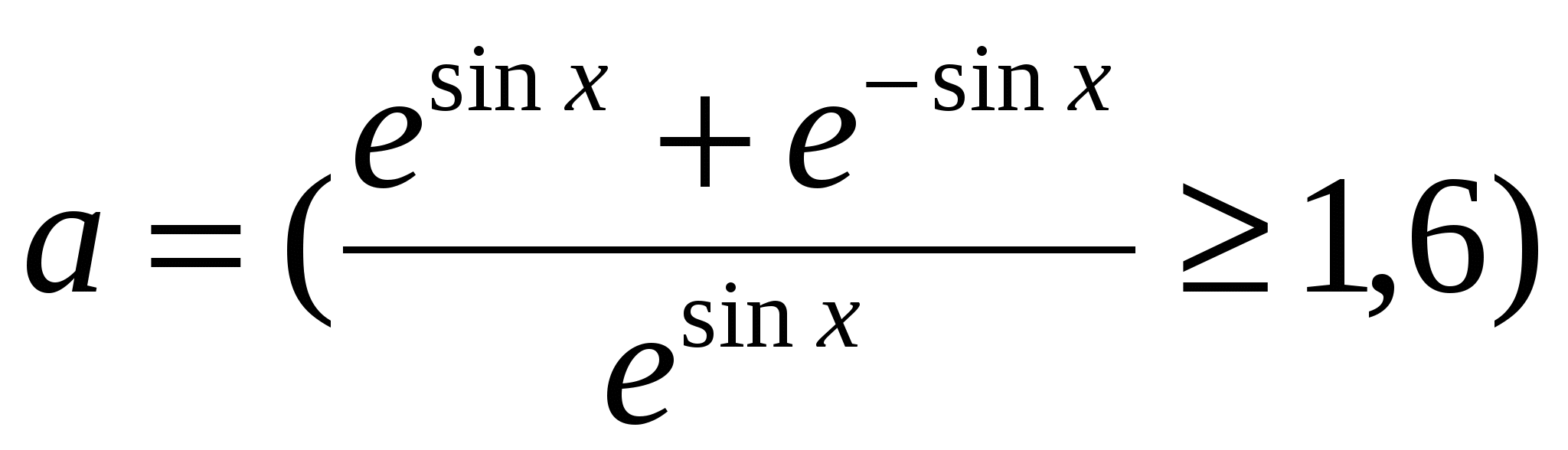 d ( b c), d ( b c),
де x = 2,09; b - TRUE; d,c - FALSE.
Обчислити 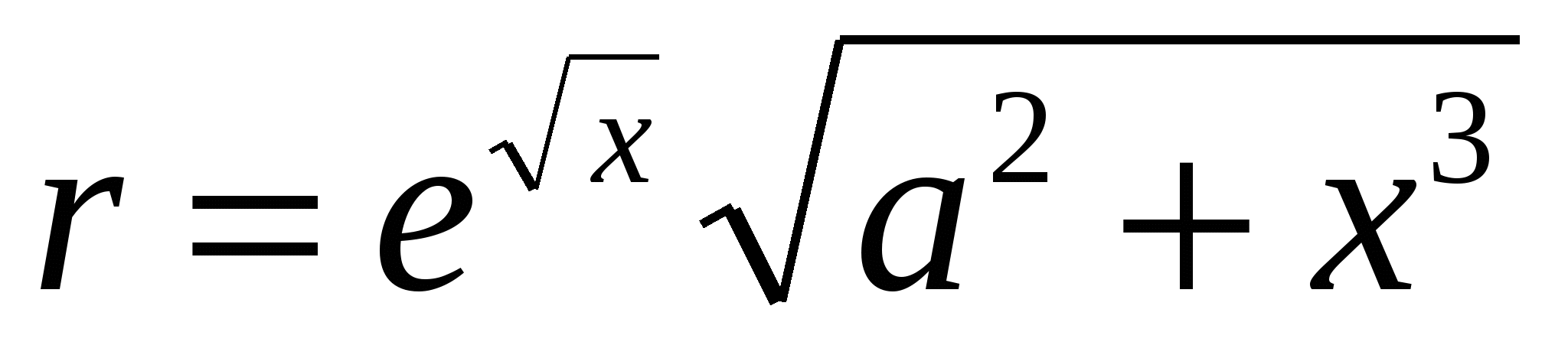 ; b= (d c (l d) d ; b= (d c (l d) d 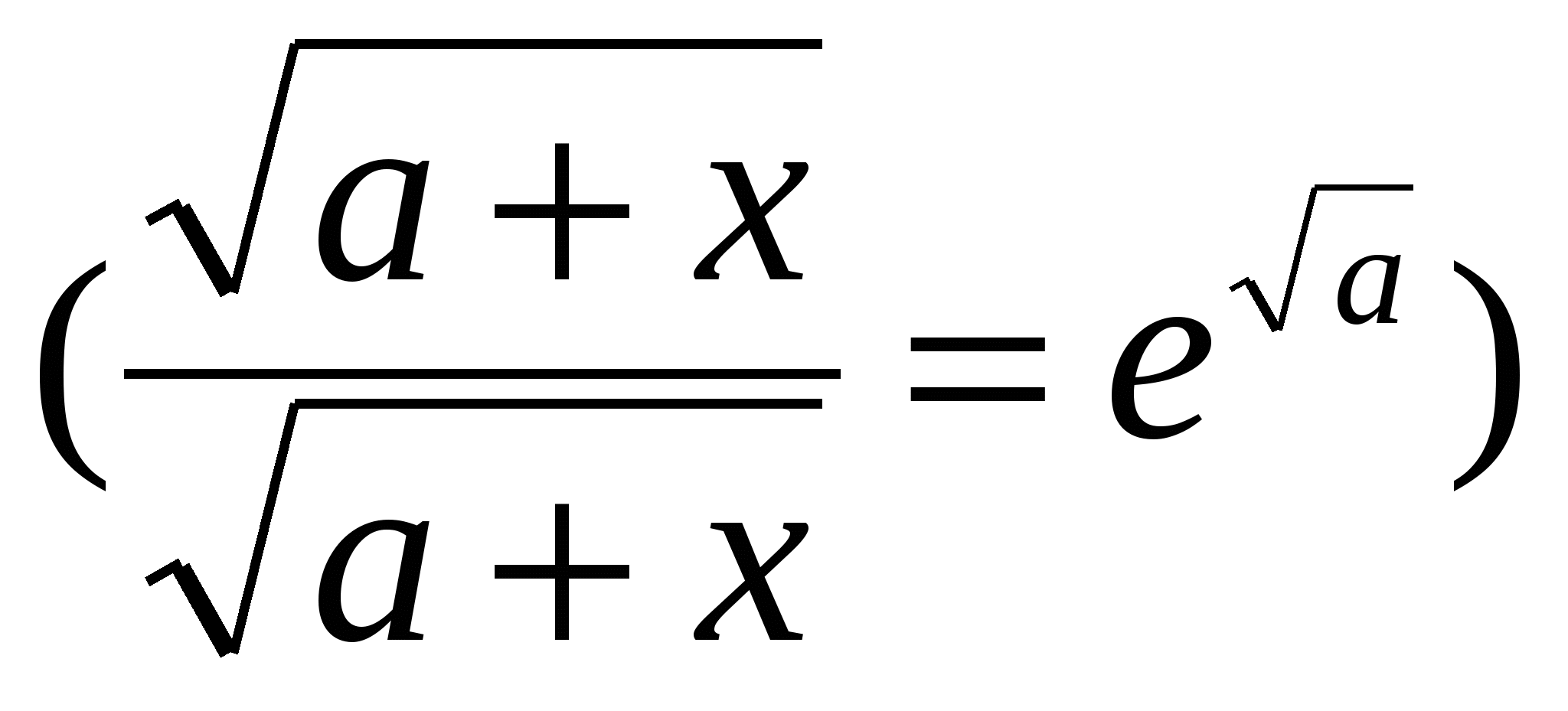 ), ),
де x = 4,27; a = 1,79; l - TRUE; d,c - FALSE.
Обчислити  ; b= d e ( d ( e d ) ; b= d e ( d ( e d ) 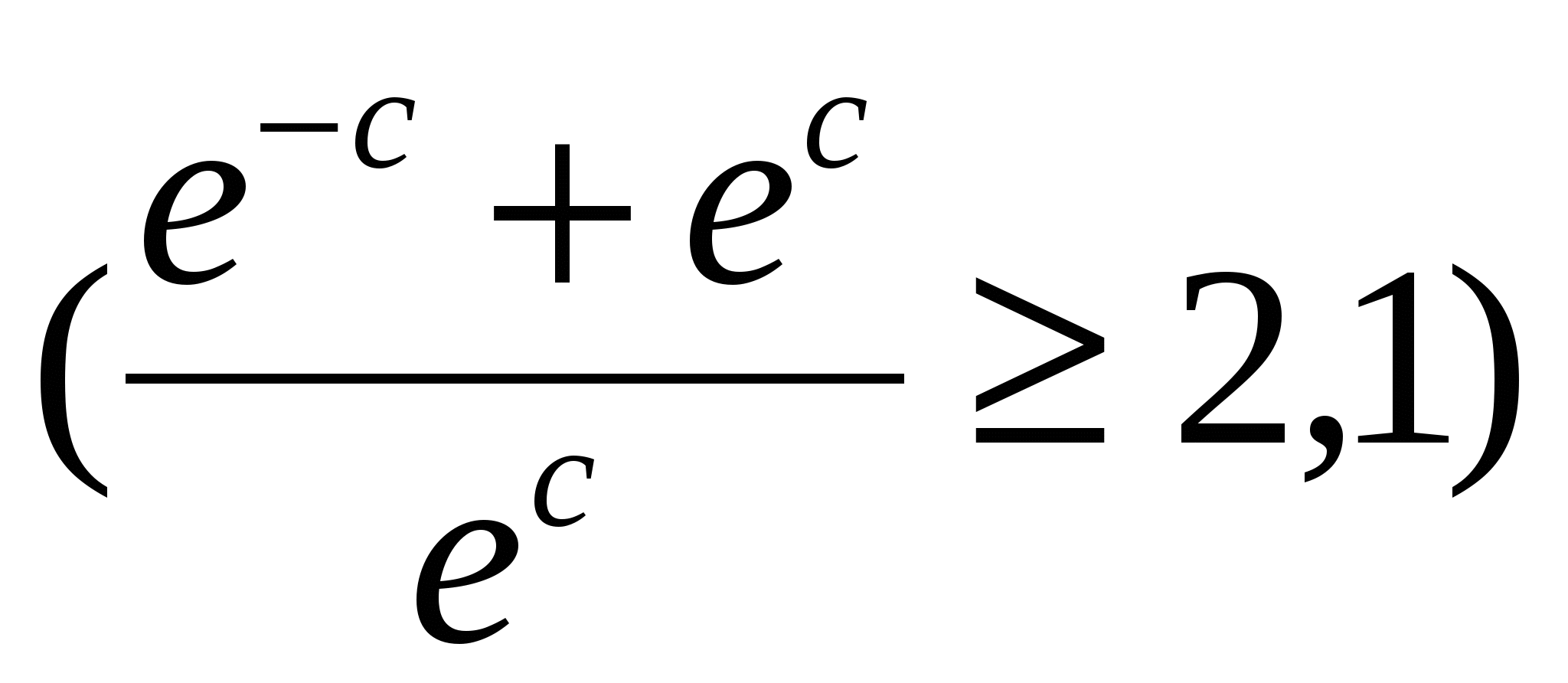 ), ),
де c = 0,93; a = 1,8; e,d - FALSE.
Обчислити 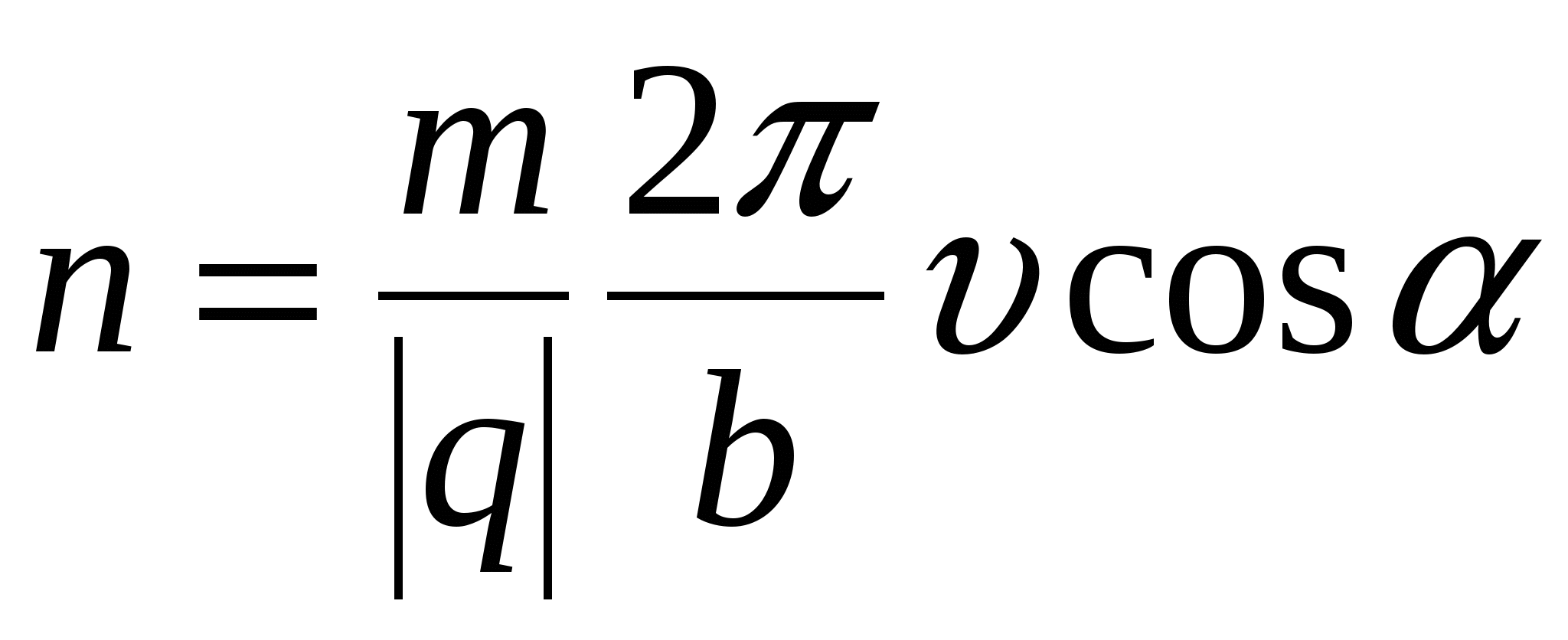 ; ; 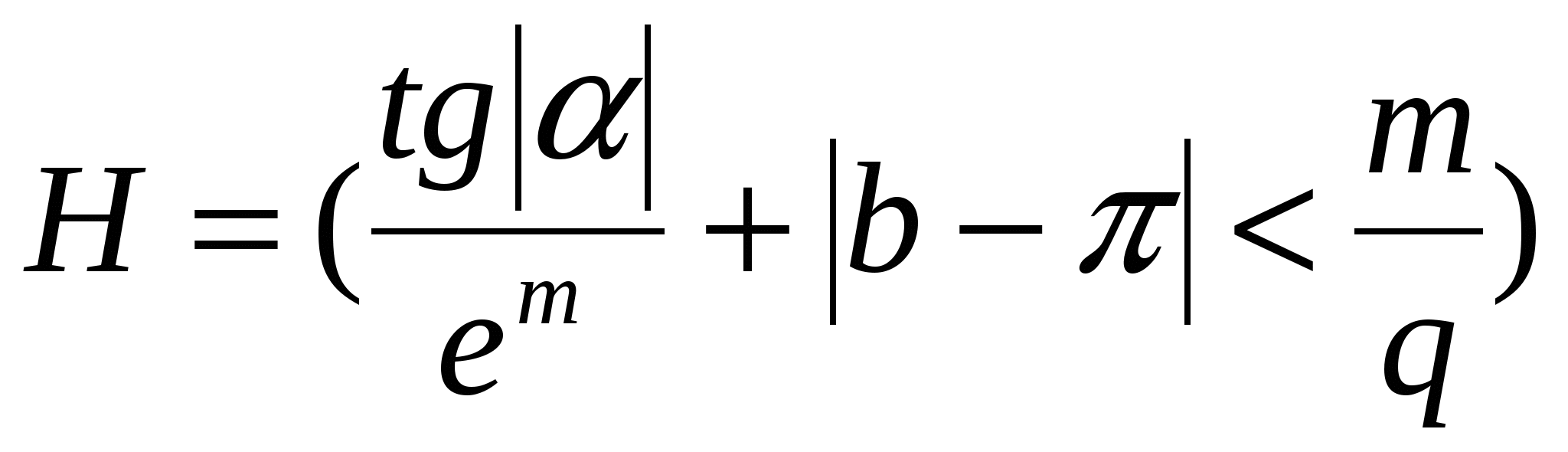 ( d c ) c, ( d c ) c,
де m = 3,12; q = 2,9; b = 6,04; = 1,77; = 0,44; d,c - FALSE.
Обчислити 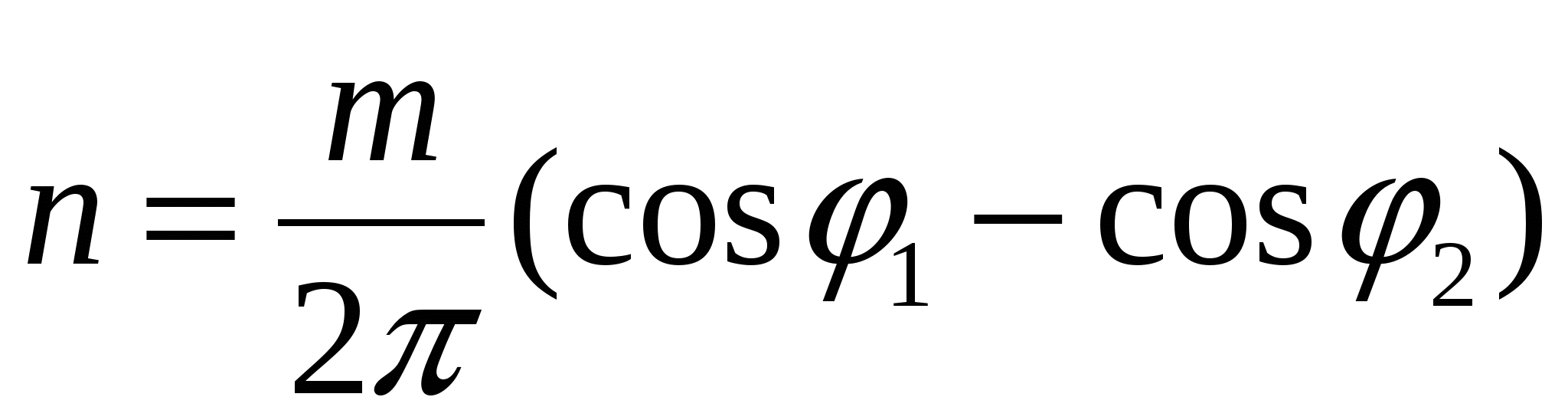 ; a= ( b c d ) b ; a= ( b c d ) b 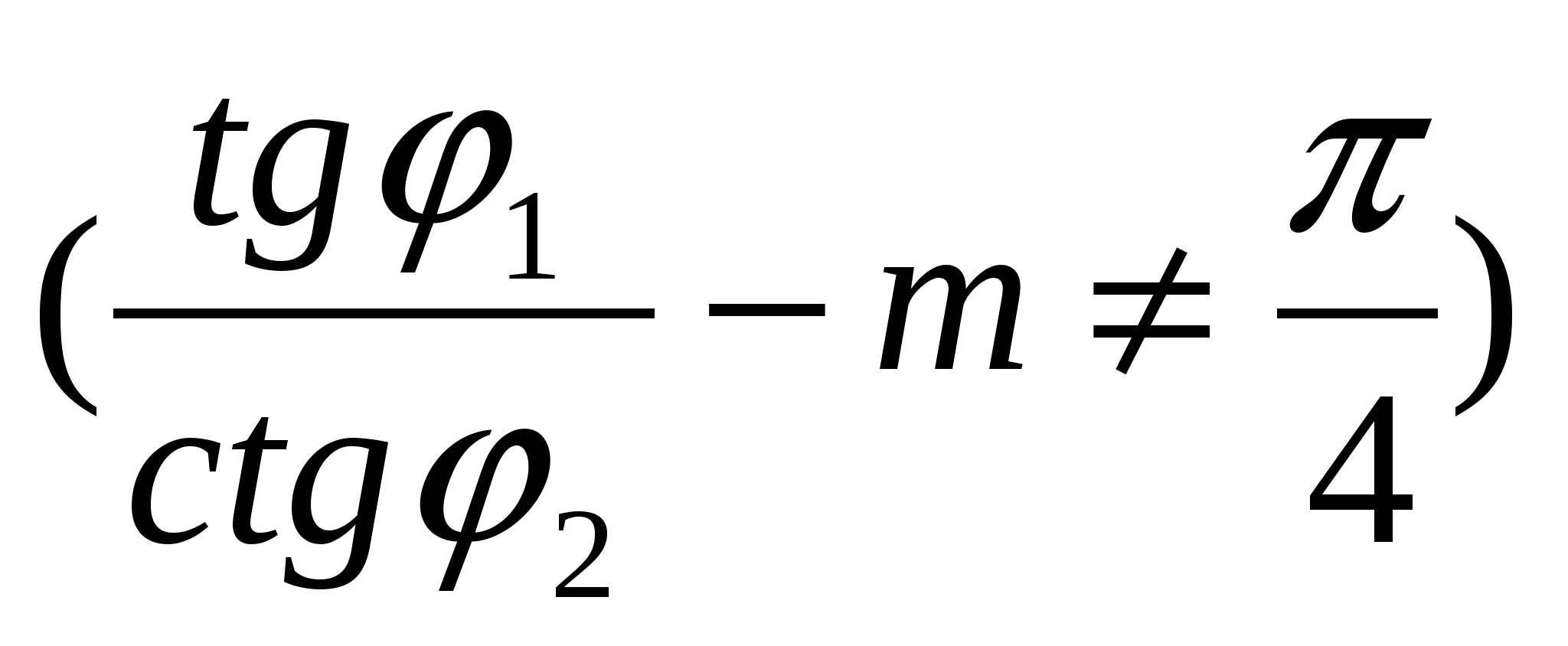 , ,
де m = 4,67; 1=0,46; 2=0,41 c- TRUE; b, d- FALSE.
Обчислити 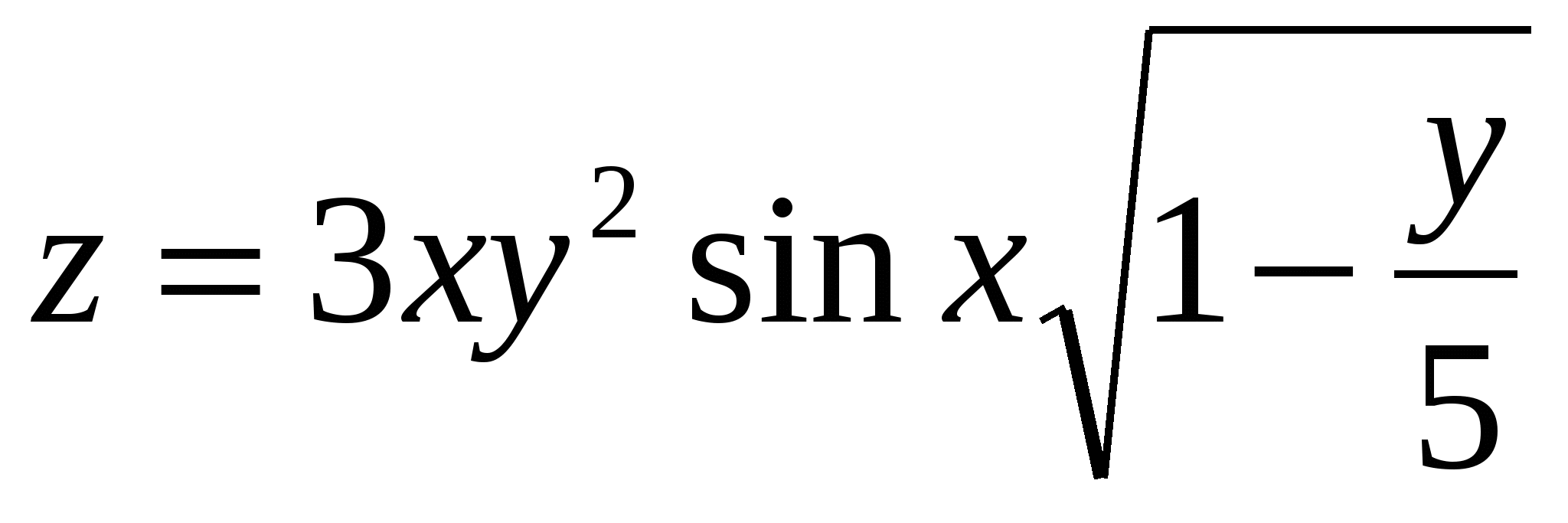 ; ; 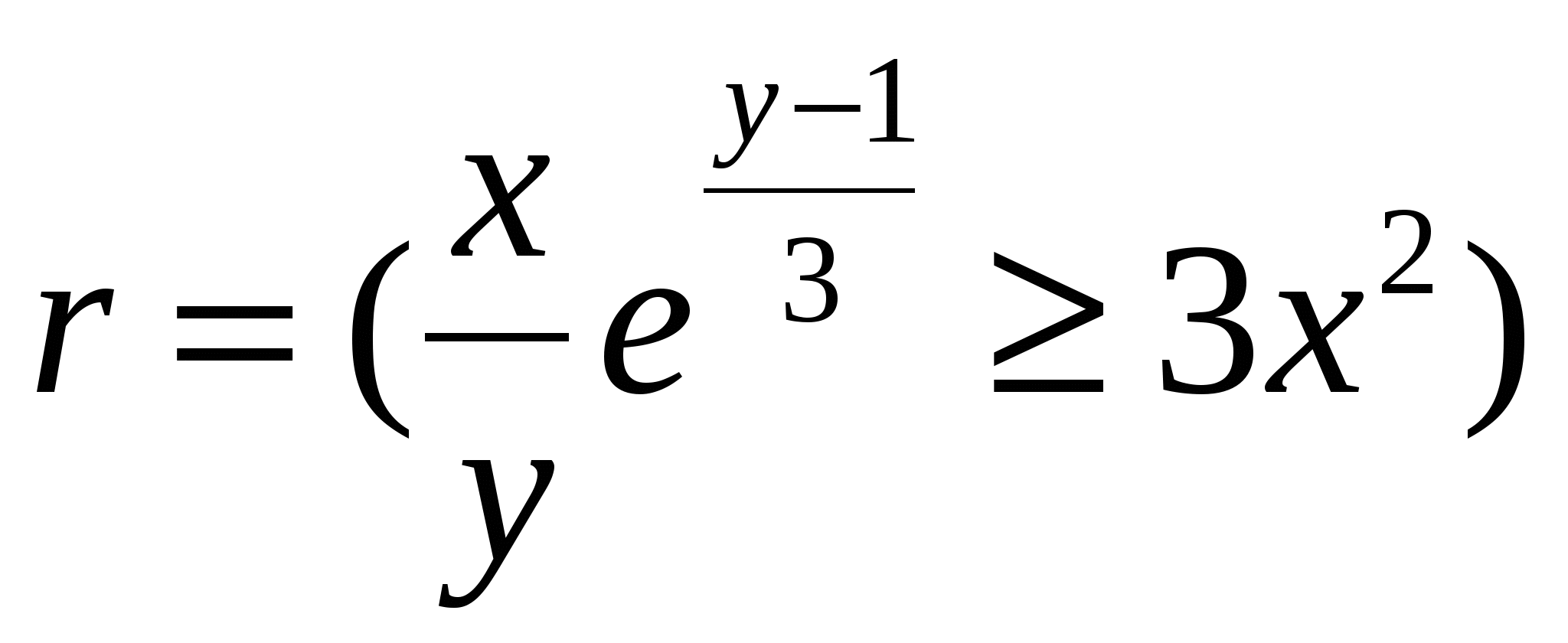 d a d, d a d,
де x = 0,93; y = 2,409; d - TRUE; a - FALSE.
Обчислити 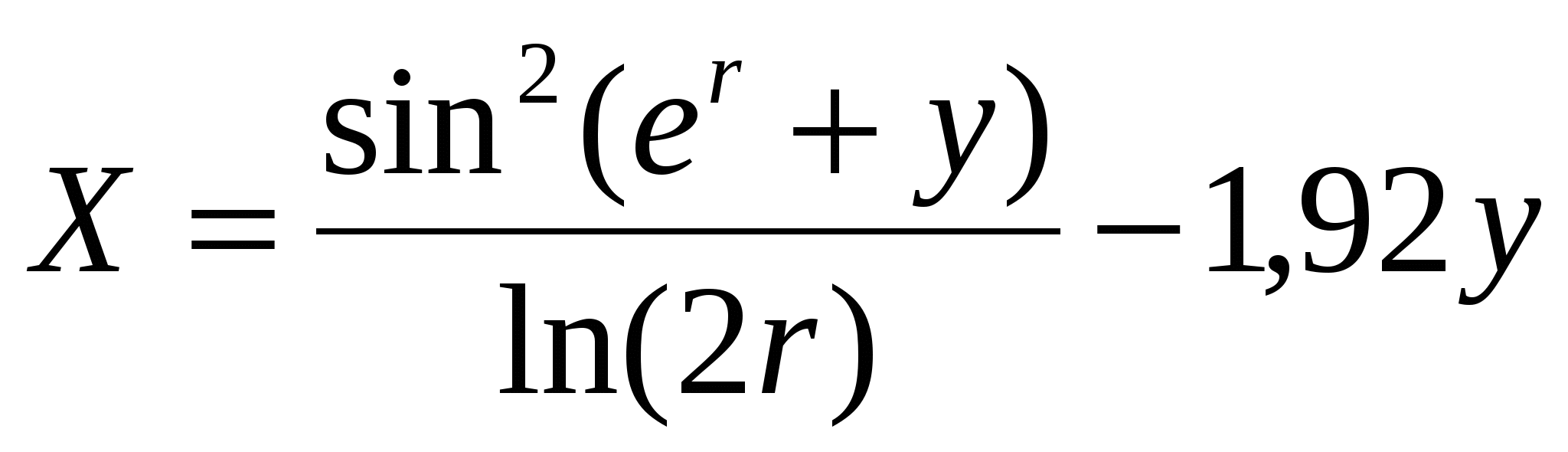 ; b = (a d) c (0,8 ; b = (a d) c (0,8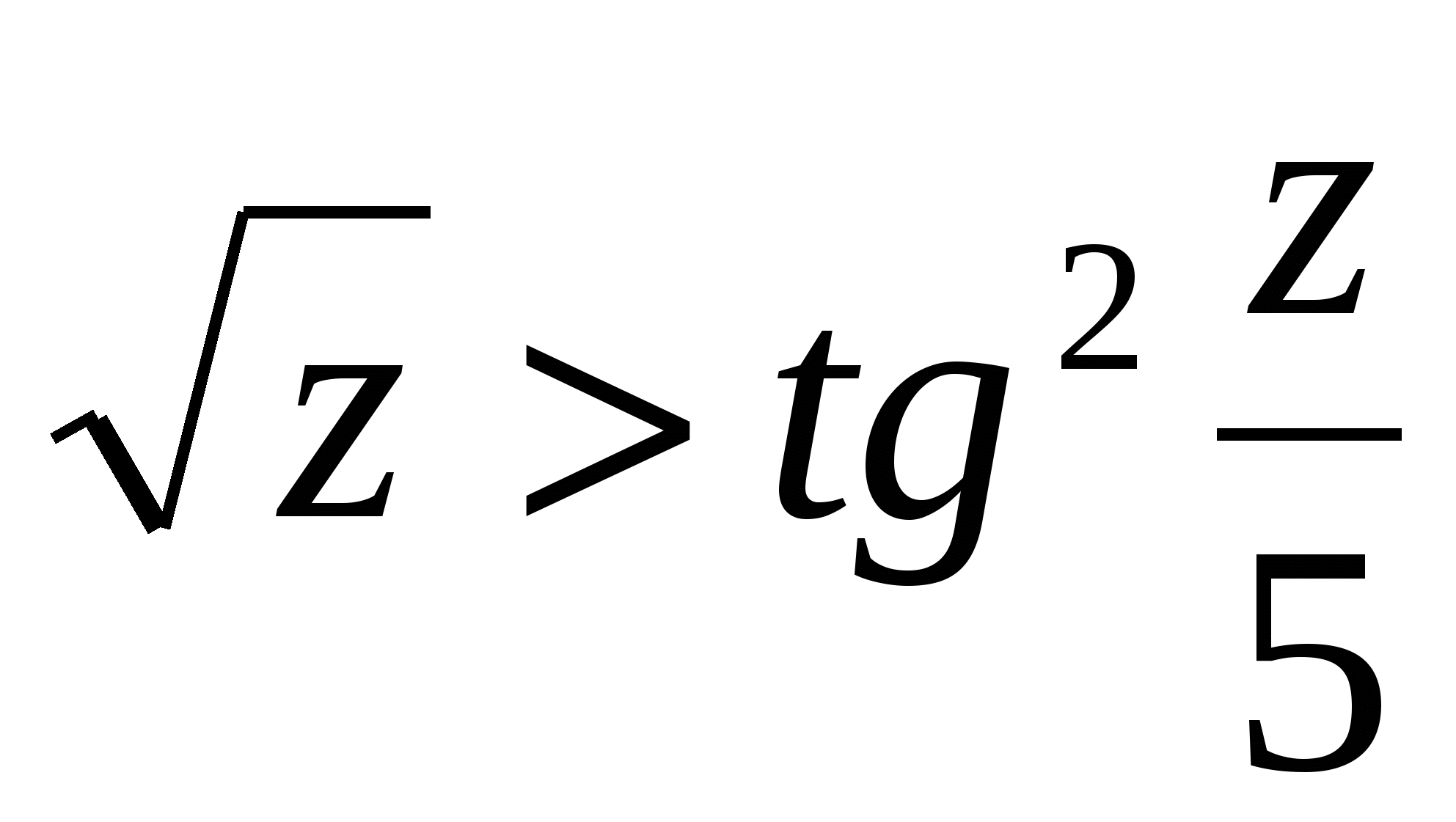 ), ),
де r = 1,912; y = 0,854; z = 1,25; a,c - TRUE; d - FALSE.
Обчислити  ; n = ((m b ) m b m) (1,7 x), ; n = ((m b ) m b m) (1,7 x),
де k = 1,4; d = 8,7; x = 9,2; m - TRUE; b - FALSE.
Обчислити 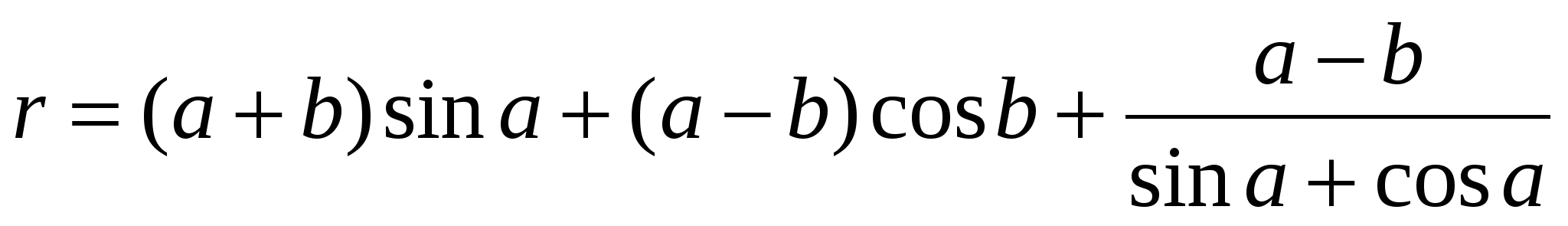 ; ;
m = ((3,6-2k) = 2,5a) (x y (x y) z),
де a = 0,22; b = 0,64; k = 0,46; x,z - TRUE; y - FALSE.
Обчислити 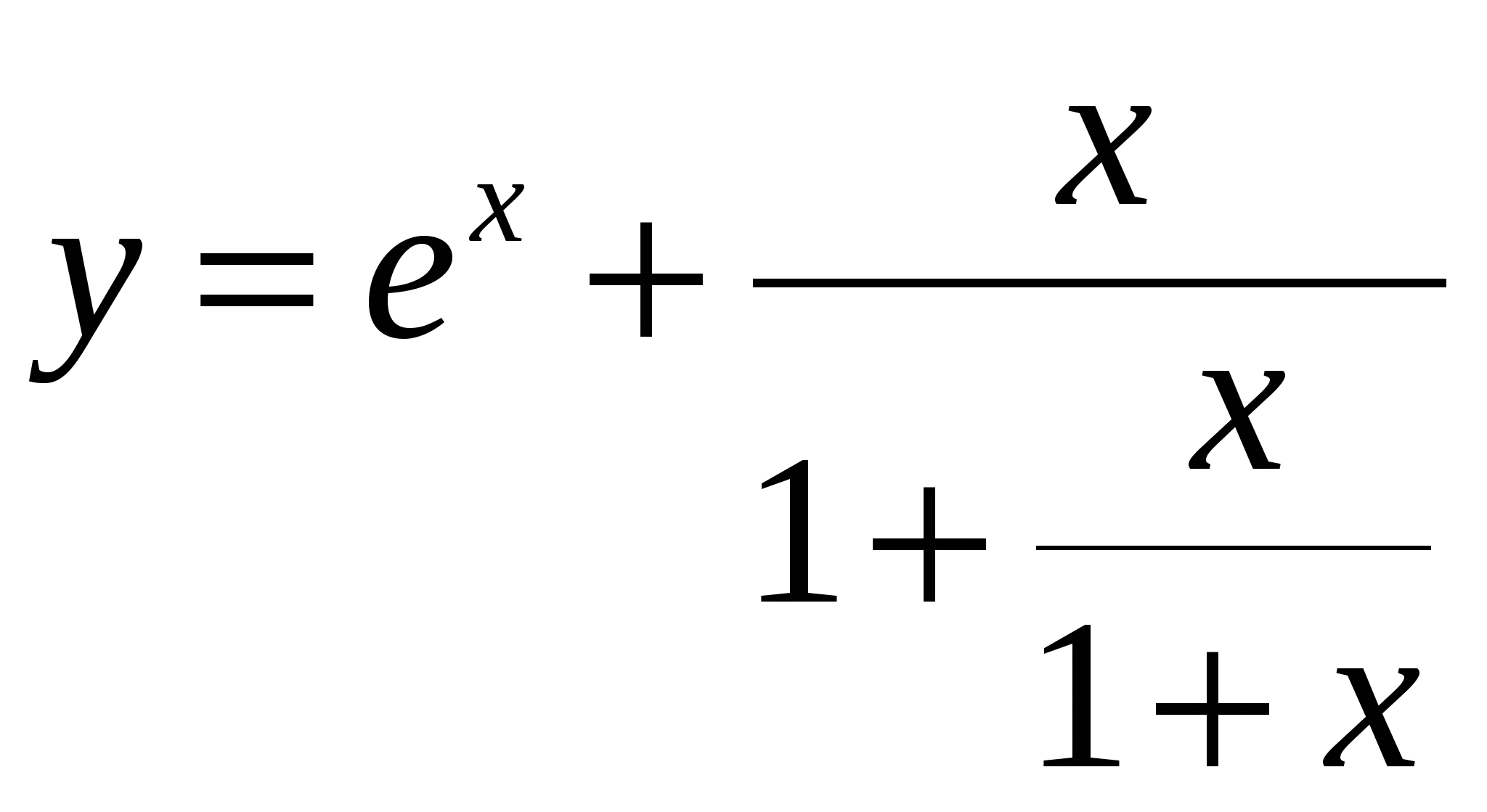 ; d= ((a+b+c)/2 ; d= ((a+b+c)/2 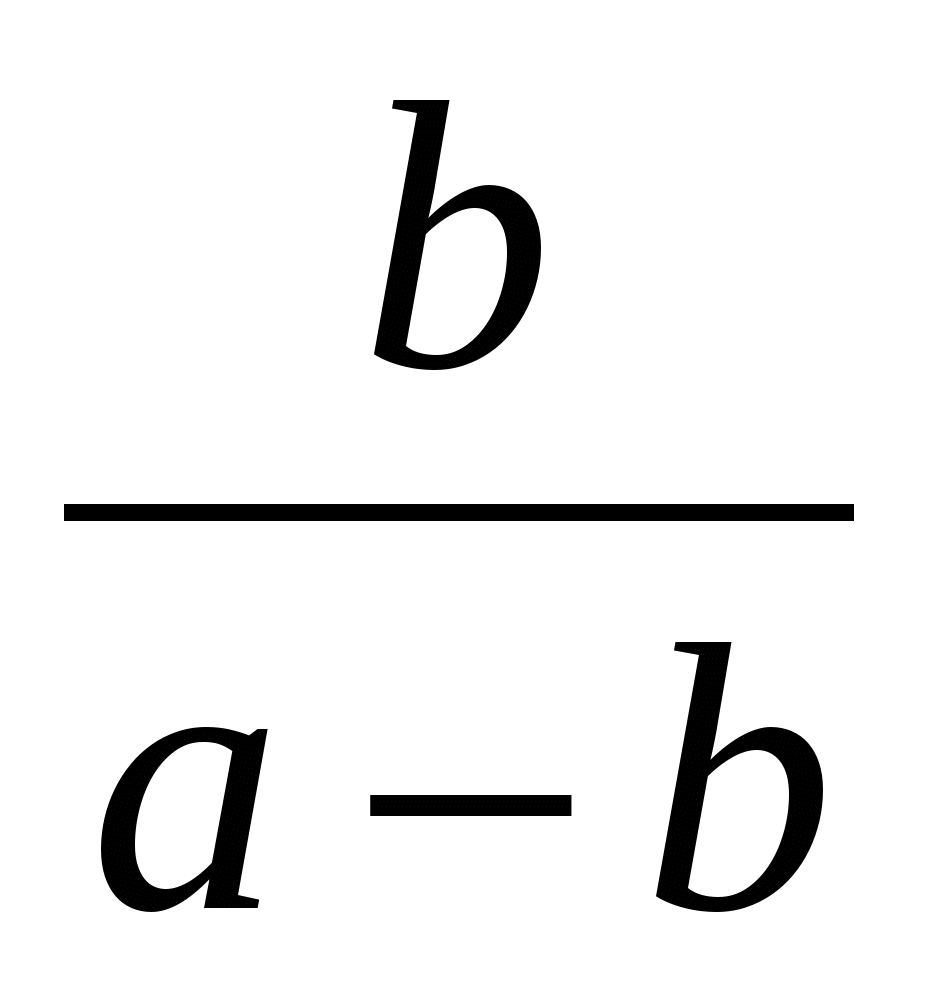 ) ((a-b) > ) ((a-b) >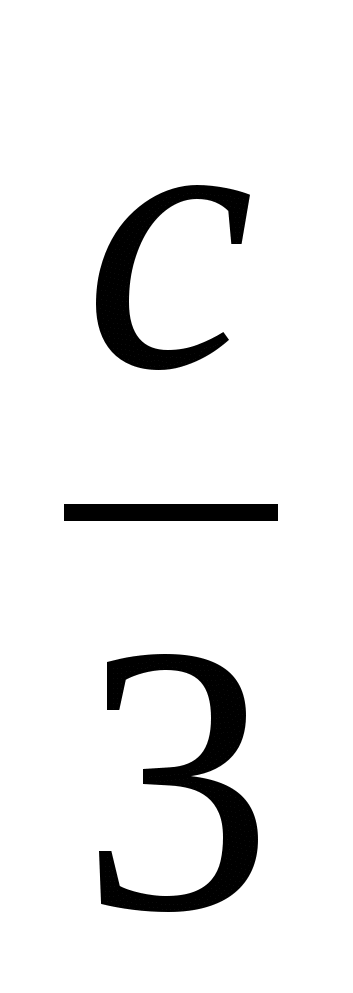 ) r, ) r,
де x = 0,2; a = 1,4; b = 0,8; c = 0,4; r - TRUE.
Обчислити 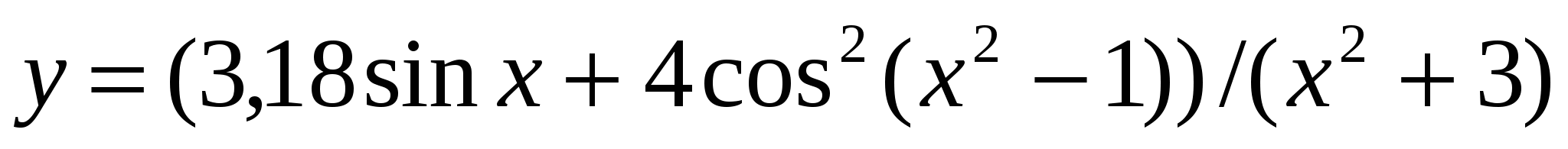 ; ;
n = p (((ab - c)b + d) > (a + b)/c) p (p q)),
де x = 0,633; a = 1,4; b = 0,99; c = 1,04; p - TRUE; q - FALSE.
Контрольні запитання
Які найпростіші конструкції мови PASCAL?
Яку структуру має програма на мові PASCAL?
Що таке константи та змінні?
Які скалярні типи даних використовуються в мові PASCAL?
Як здійснюється опис типу змінних?
Які є оператори введення та виведення?
Які формати виведення змінних і констант?
Які особливості виведення текстових змінних і констант?
Як здійснюється керування виведенням інформації?
Як записуються арифметичні вирази?
Який вигляд мають логічні вирази?
Які оператори присвоювання є в мові PASCAL?
Які логічні операції використовуються в логічних операторах присвоювання?
Які операції відношень використовуються в логічних операторах присвоювання?
Яка послідовність виконання арифметичних і логічних операторів присвоювання?
ЛАБОРАТОРНА РОБОТА 4
ПРОГРАМУВАННЯ АЛГОРИТМІВ РОЗГАЛУЖЕНОЇ СТРУКТУРИ
Мета роботи: отримання практичних навиків розробки алгоритмів розгалуженої структури і складання програм, що реалізують ці алгоритми.
Робоче завдання
Скласти алгоритм і розробити програму, що виконують такі дії:
виведення заголовка лабораторної роботи, у якому вказується найменування лабораторної роботи, її номер, варіант індивідуального завдання, прізвище студента та навчальна група;
введення початкових даних у діалоговому режимі;
здійснення обчислень відповідно до умови варіанта індивідуального завдання;
виведення початкових даних і результатів обчислень із їх іменами.
Варіанти індивідуальних завдань для виконання лабораторної роботи.
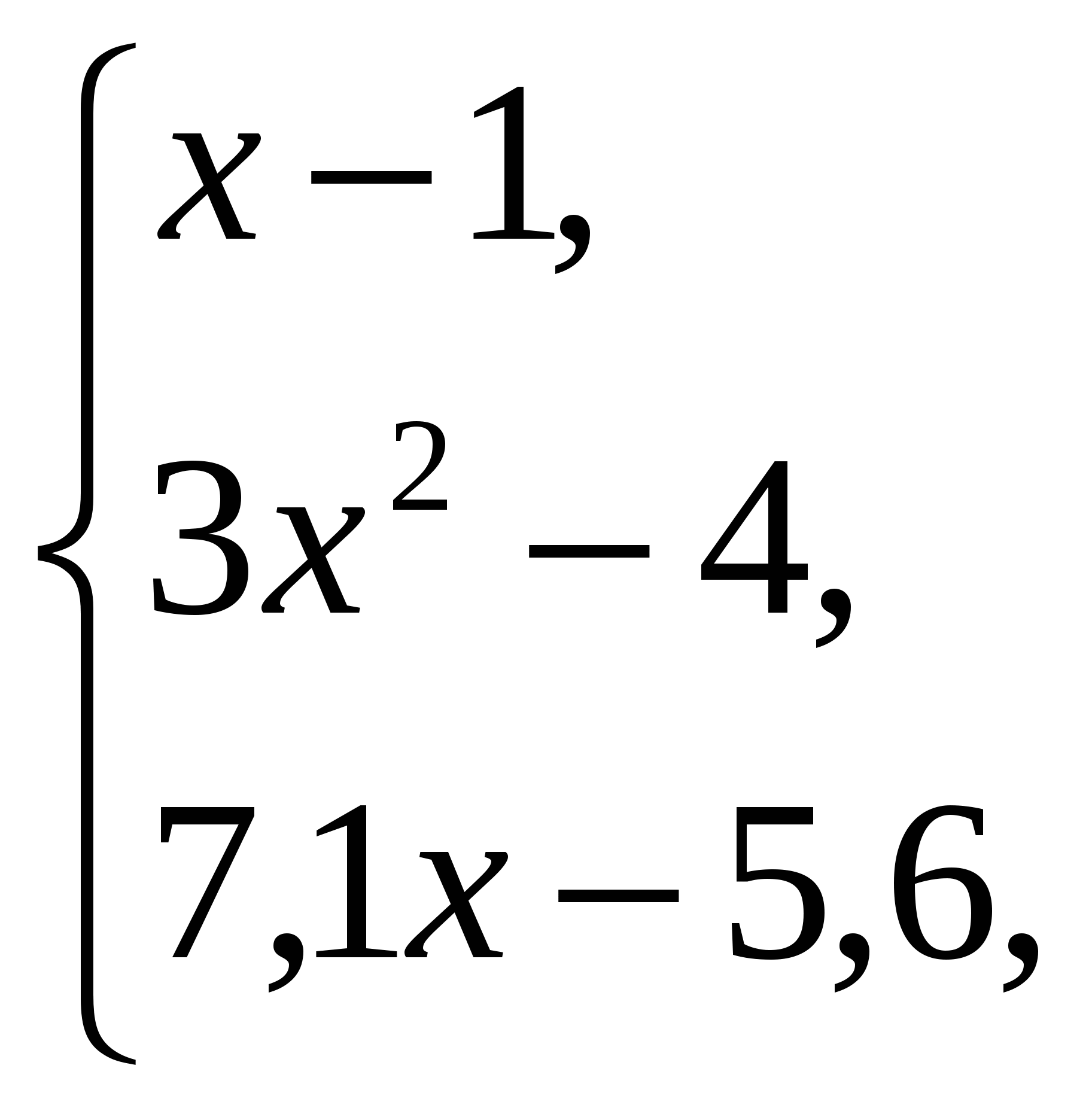
Обчислити якщо x 5;
якщо 5 x 10;
інакше.
О
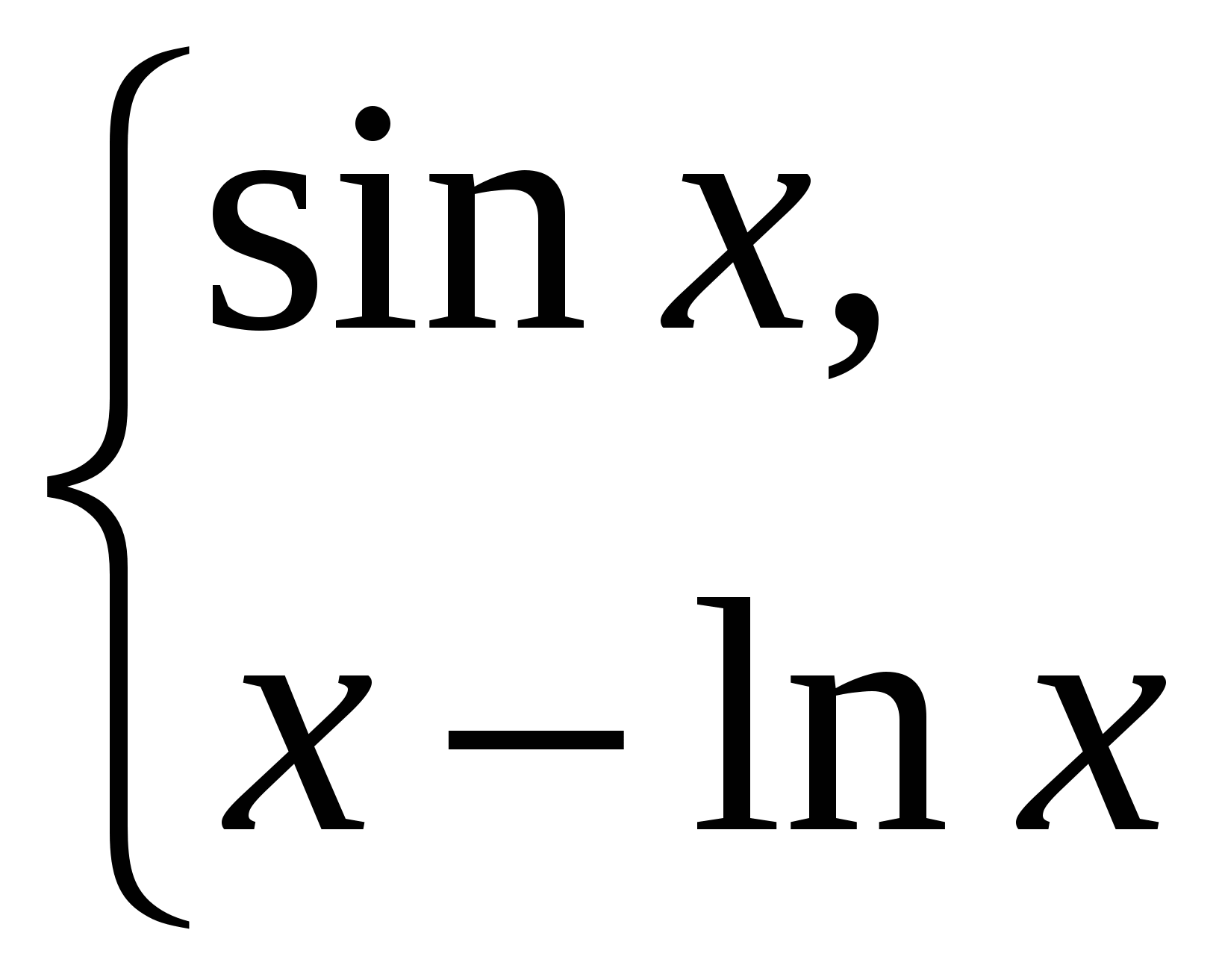
бчислити якщо x 1;
інакше.
О
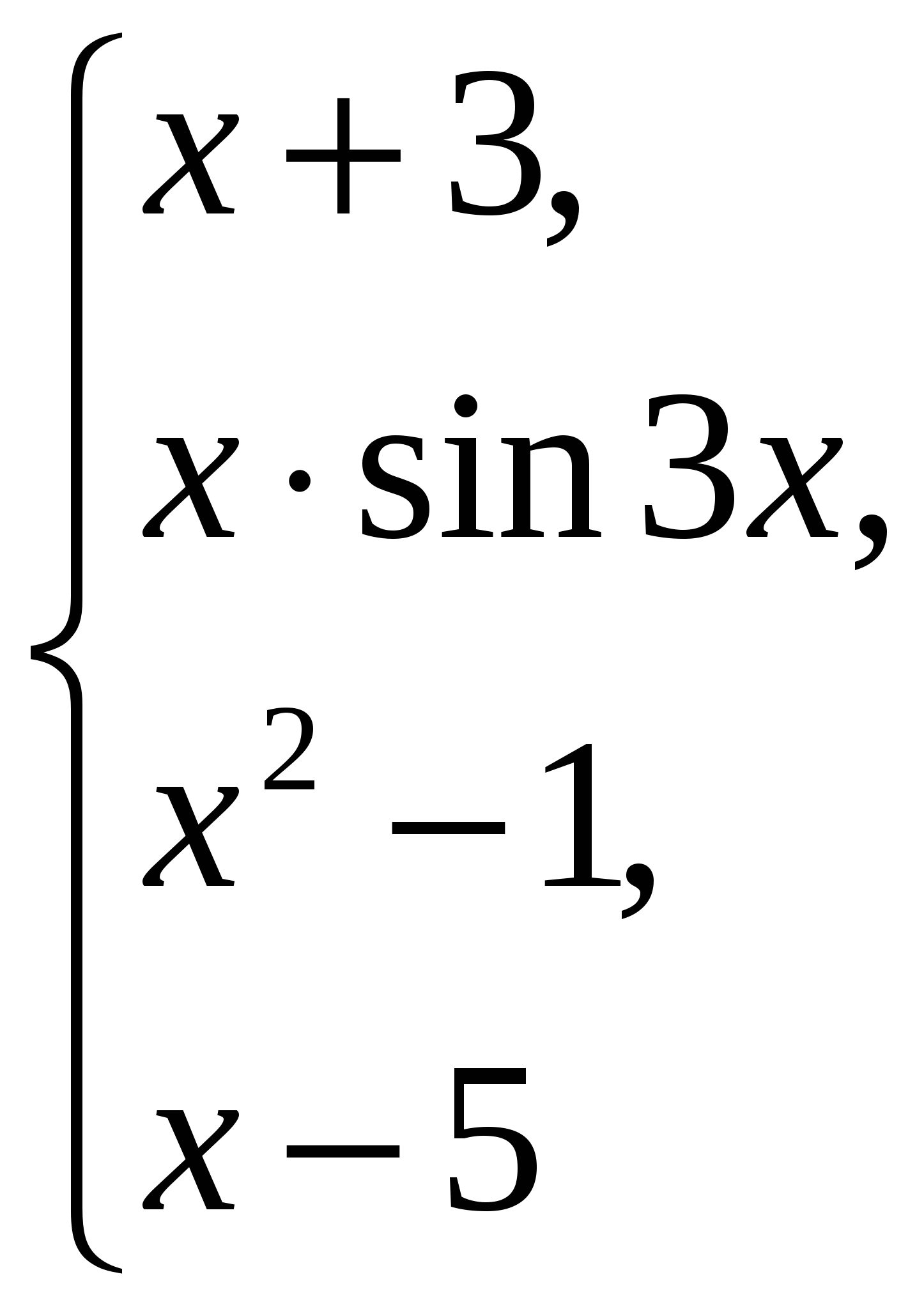
бчислити якщо x 0;
якщо 0 x 1,5;
якщо 1,5 x 2,5;
інакше.
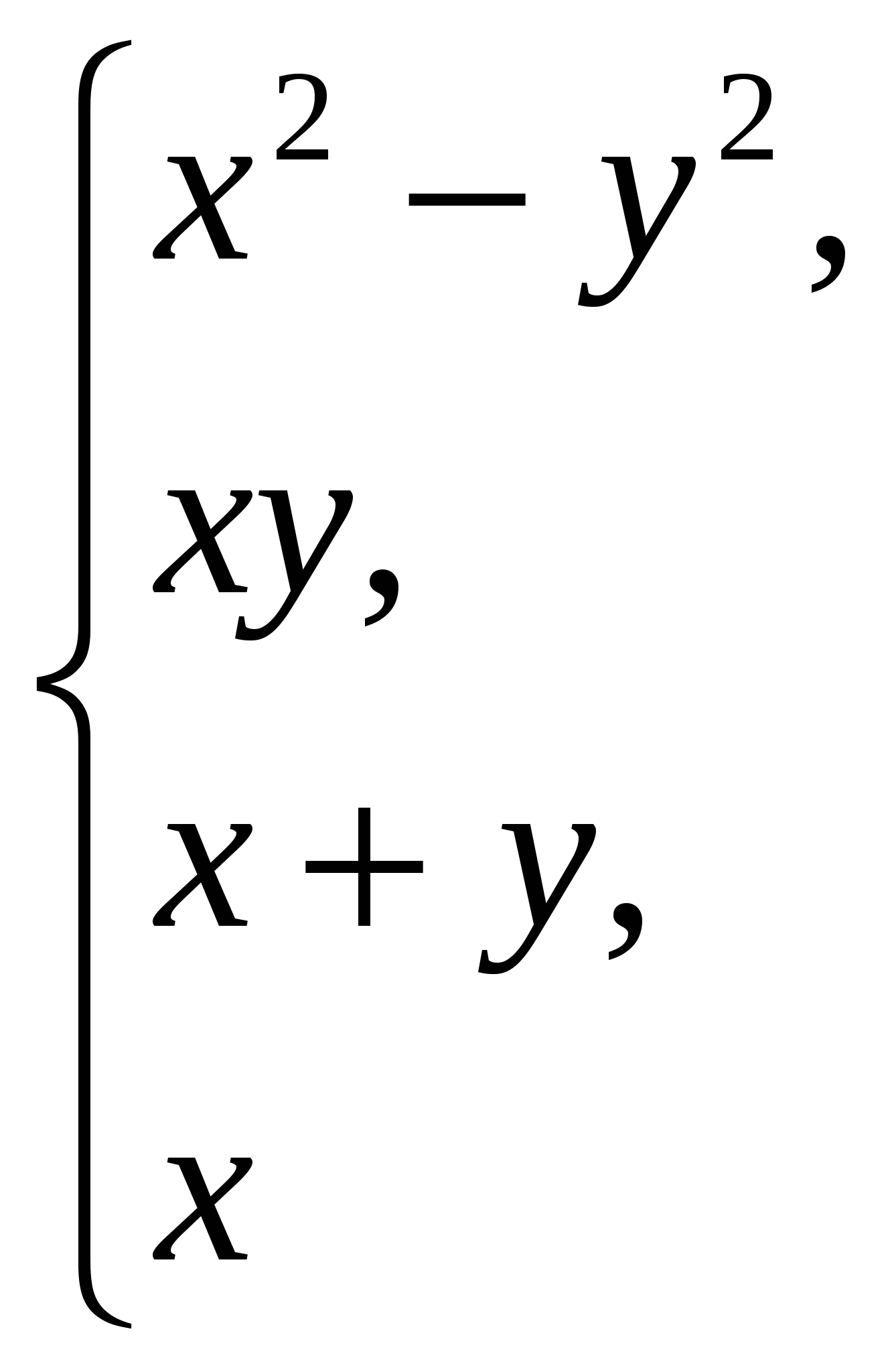
Обчислити якщо x y і y 0;
якщо x y і y 0;
якщо x y і y 0;
інакше.
О
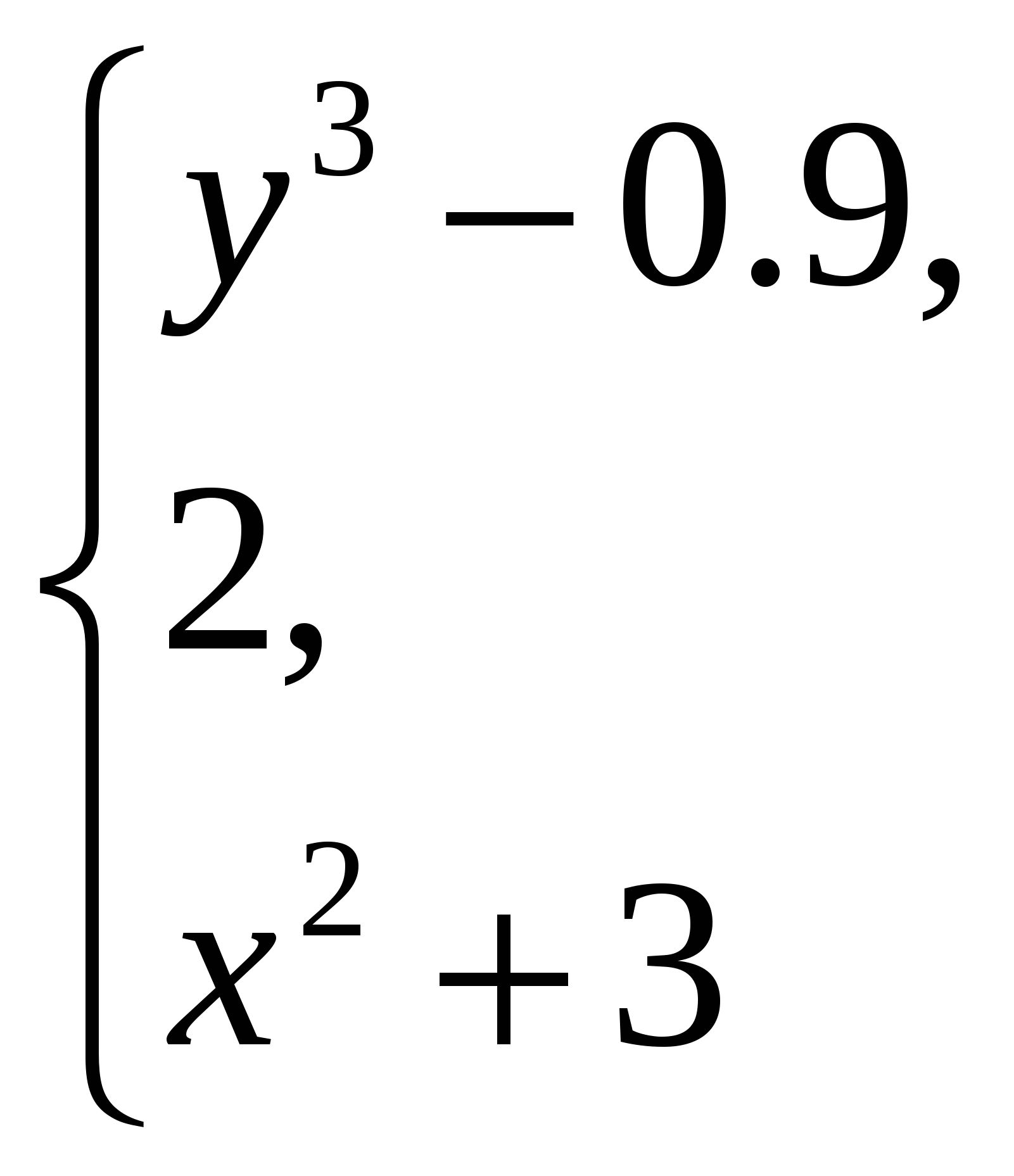
бчислити якщо y 0;
якщо 0 y 1;
інакше.
О
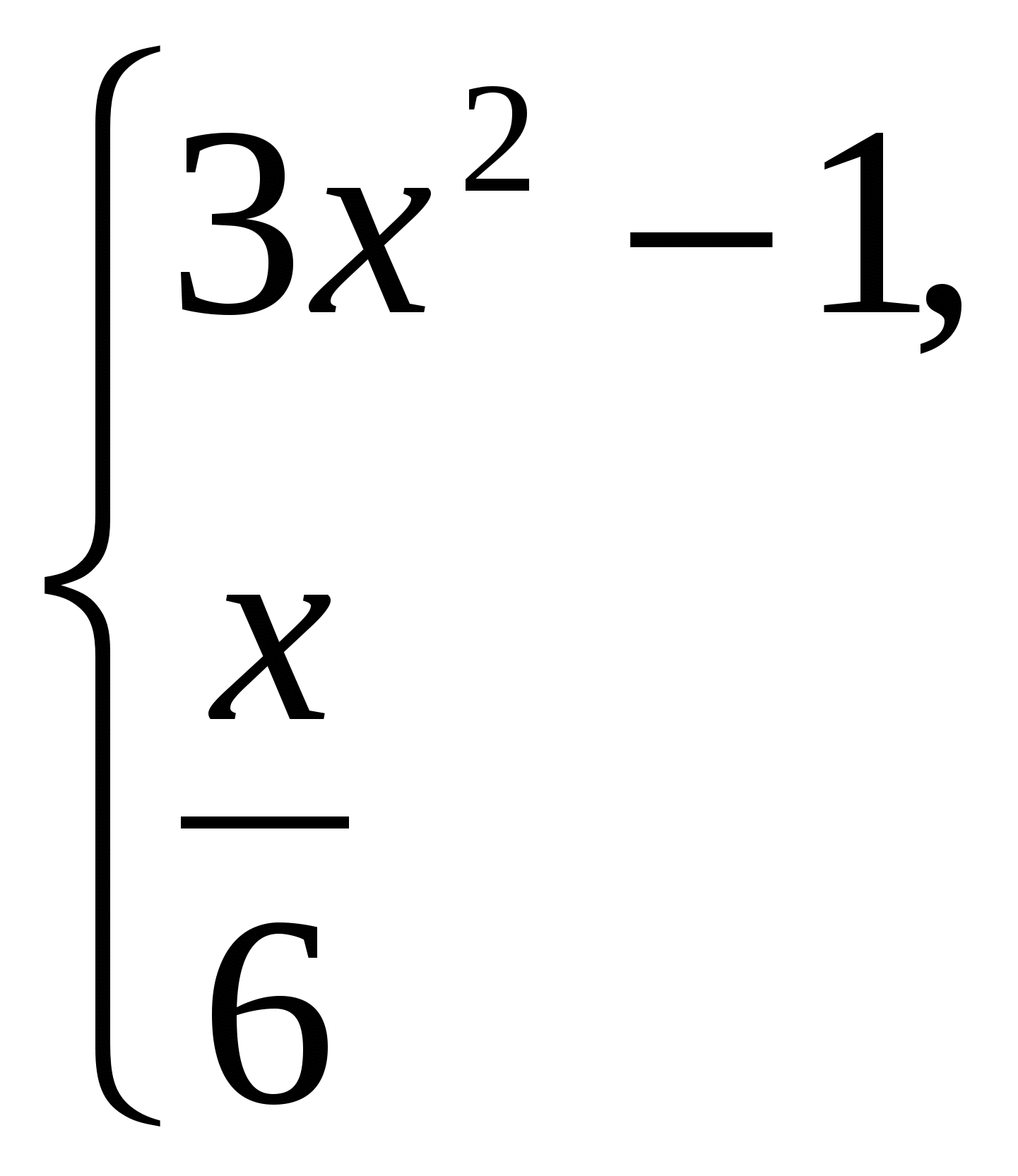
бчислити якщо x (a,b);
інакше.
О
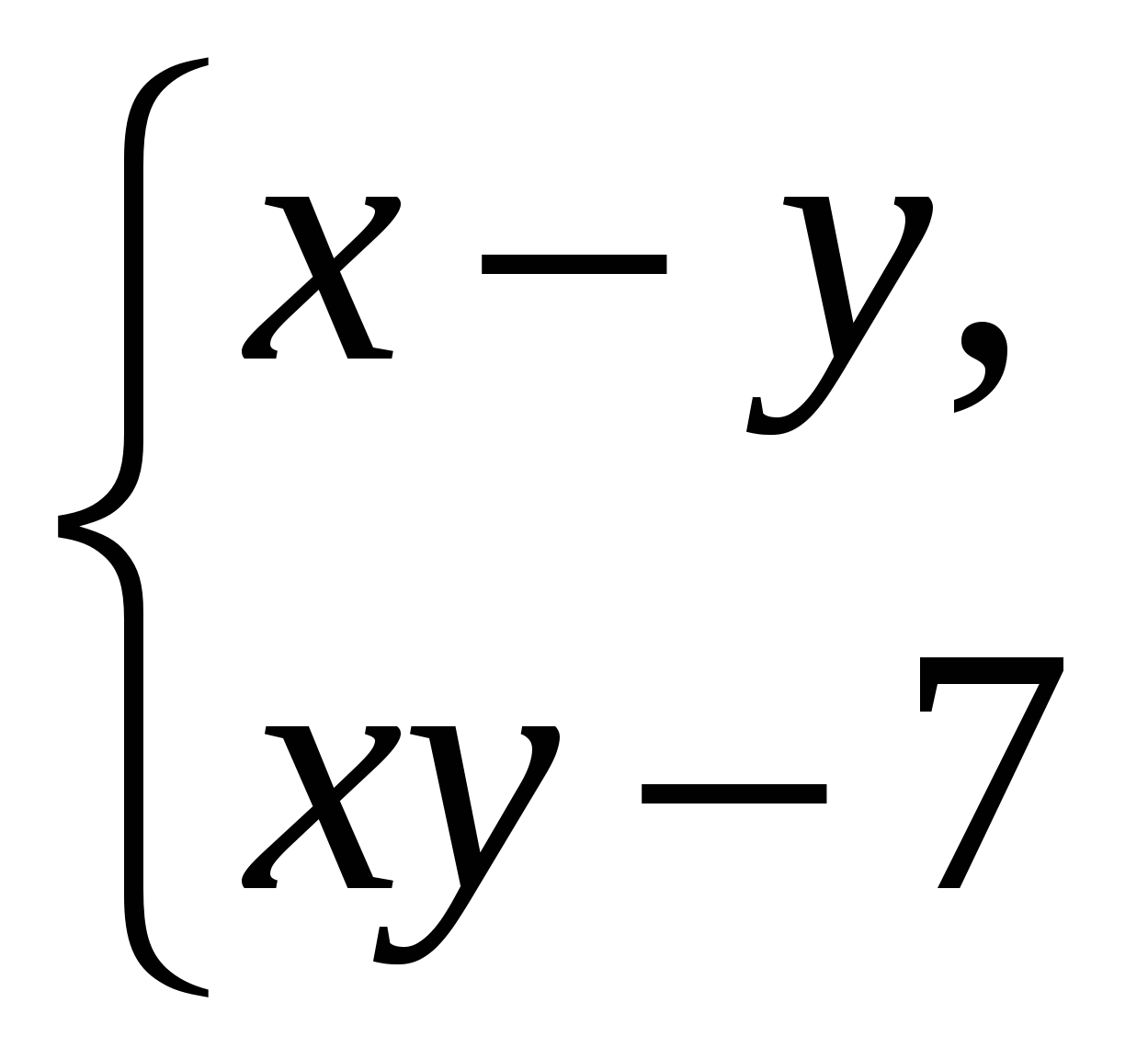
бчислити якщо x,y (a,b);
інакше.
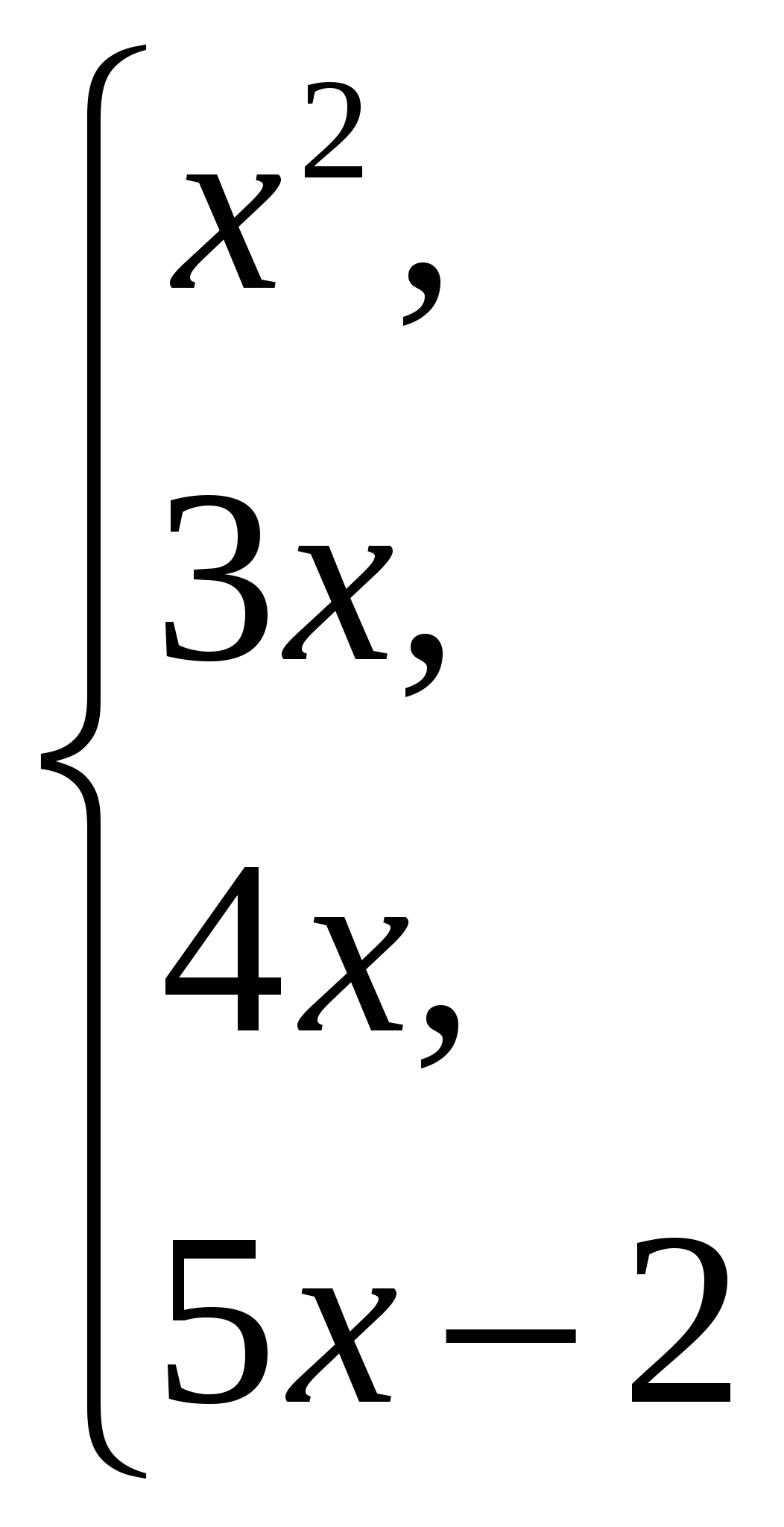
Обчислити якщо k = 1
якщо k = 2;
якщо k = 3;
інакше.
О

бчислити якщо x 3;
якщо 3 x 7;
інакше.
Визначити, чи належить точка А з координатами x і y прямій, що задана рівнянням y = 1,3-1,2x.
Визначити, якому квадранту належить точка D(x,y).
Визначити, чи належить точка А(x,y) трикутнику, заданому координатами вершин У(3;1,1), С(0,8;-3,1), D(1,4;5).
Визначити, чи належить точка А(x,y) трикутнику утвореному осями OX і OY і прямою у = 2,1х-1,7.
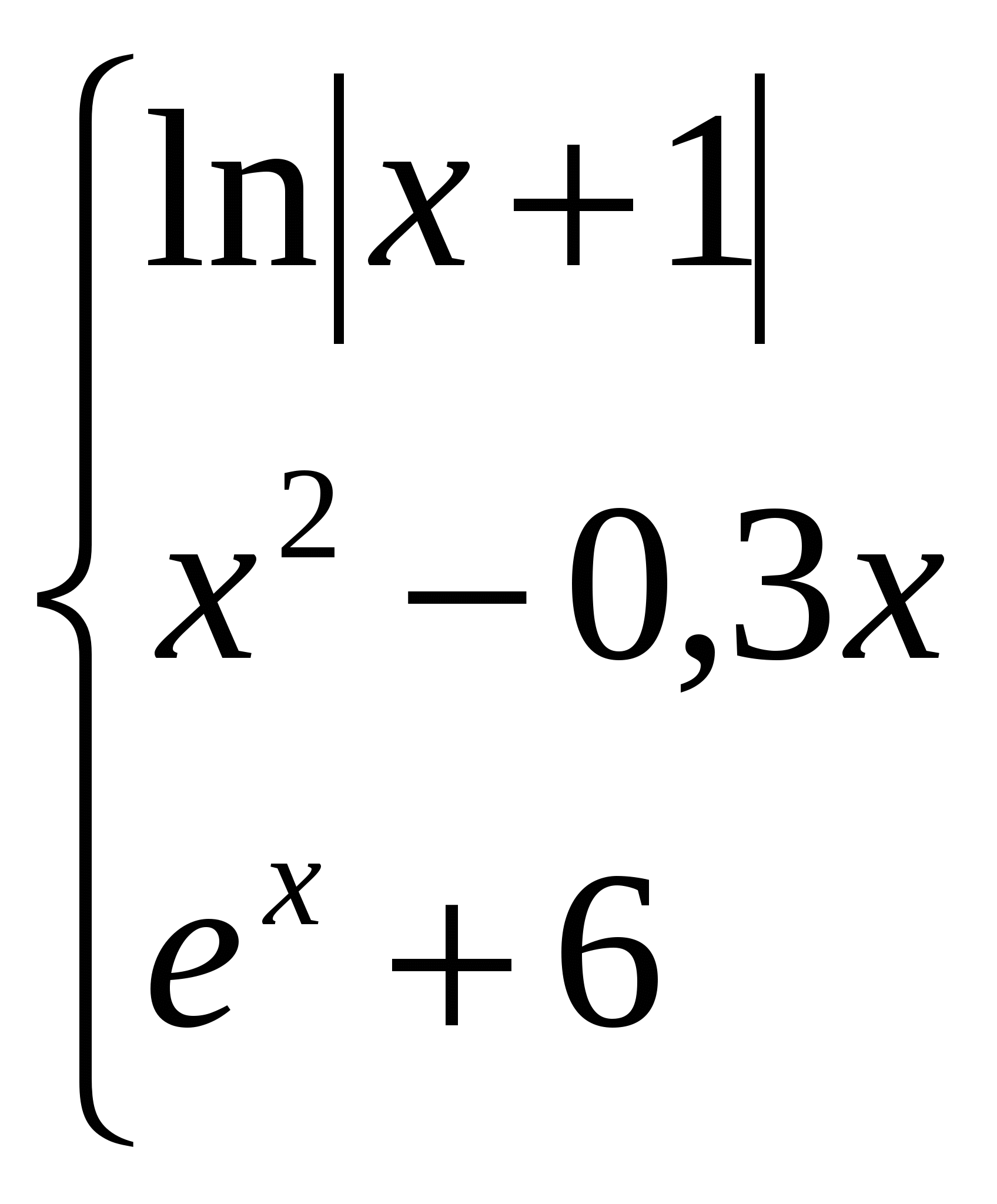
Обчислити якщо x 1;
якщо -1 x 1;
інакше.
О
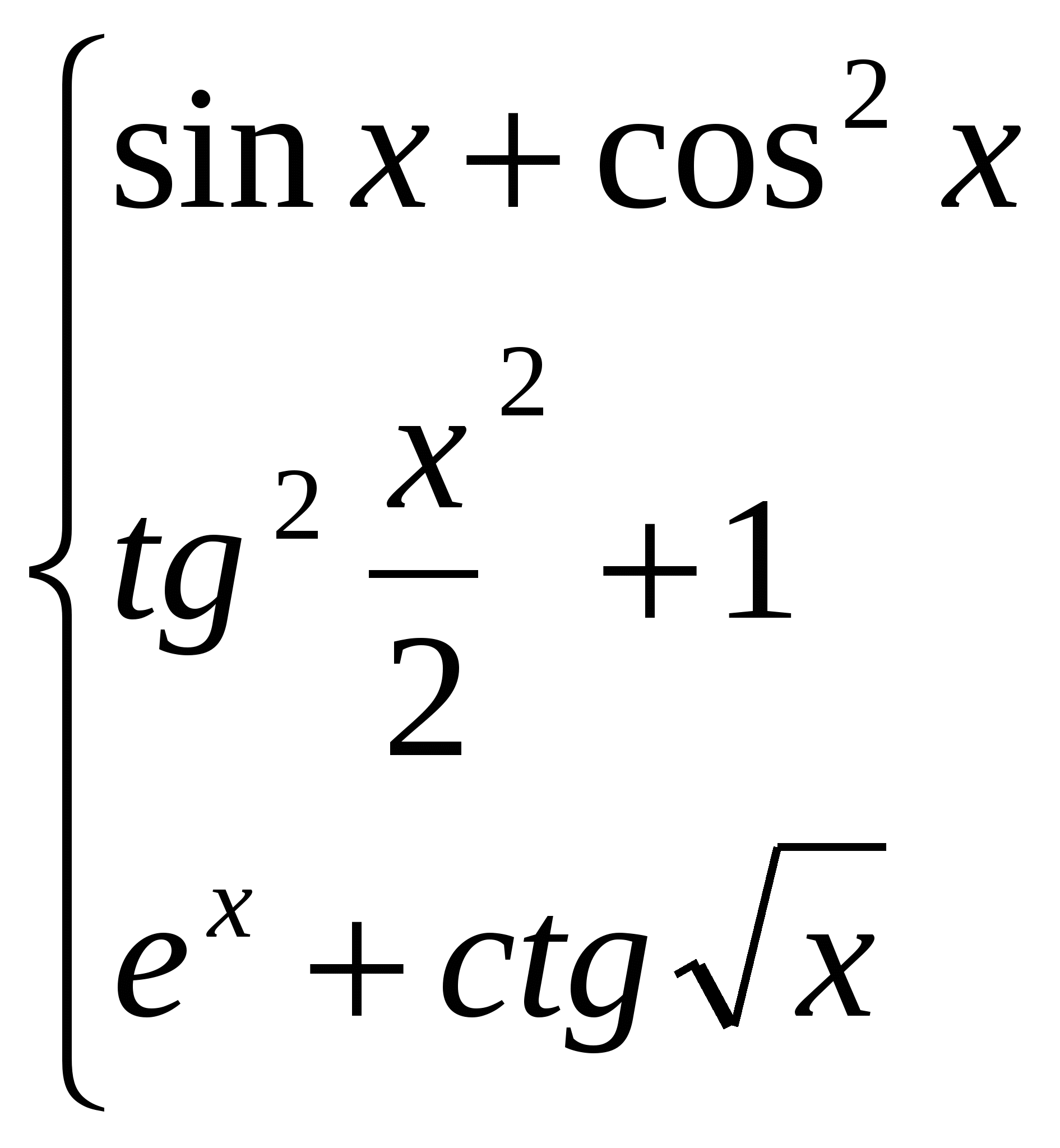
бчислити якщо x 0,3;
якщо 0,1 x 0,3;
інакше.
О
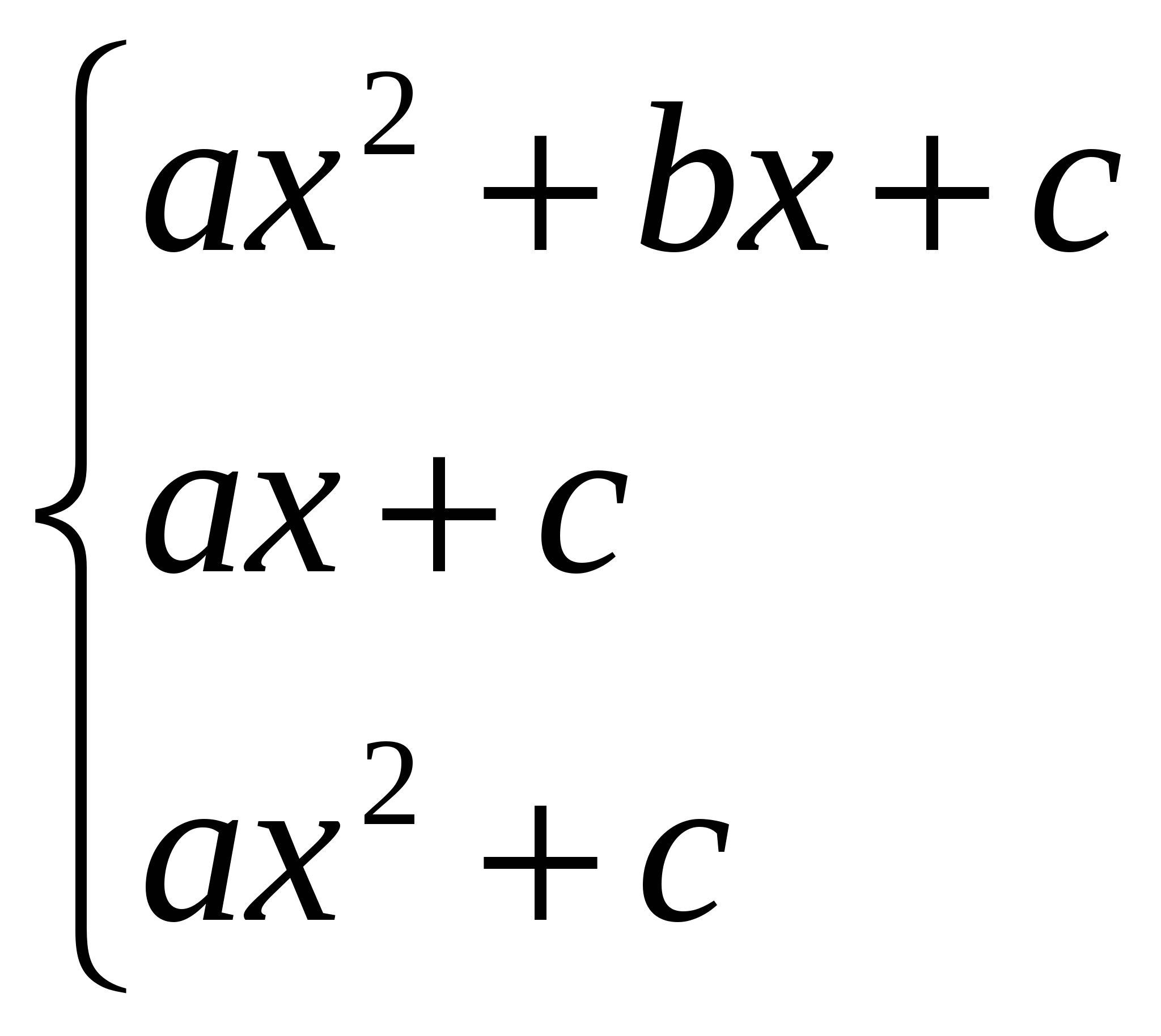
бчислити якщо 1 x 3;
якщо x 3;
інакше.
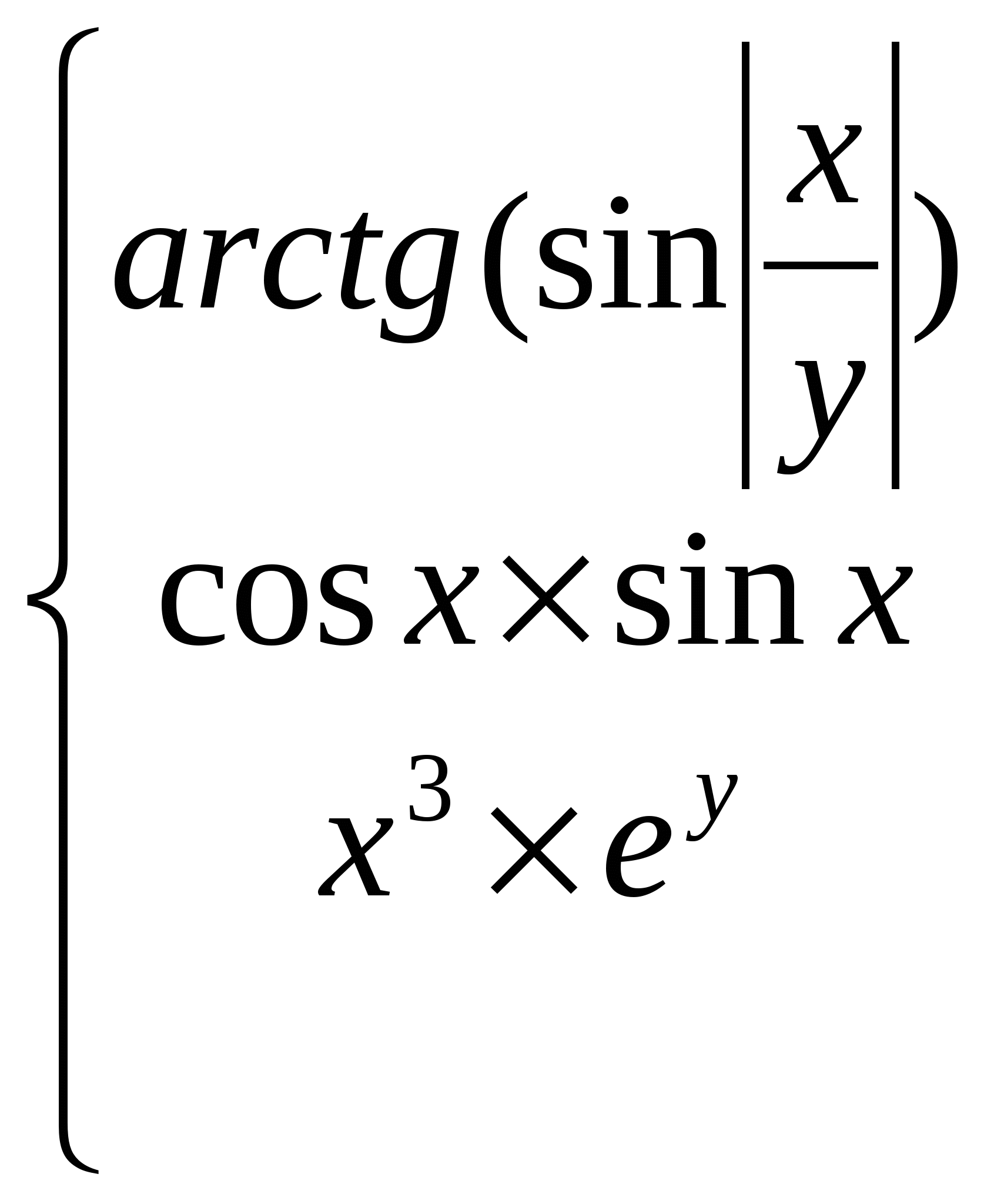
Обчислити якщо y x і x 0;
якщо x y і y 0;
інакше.
О
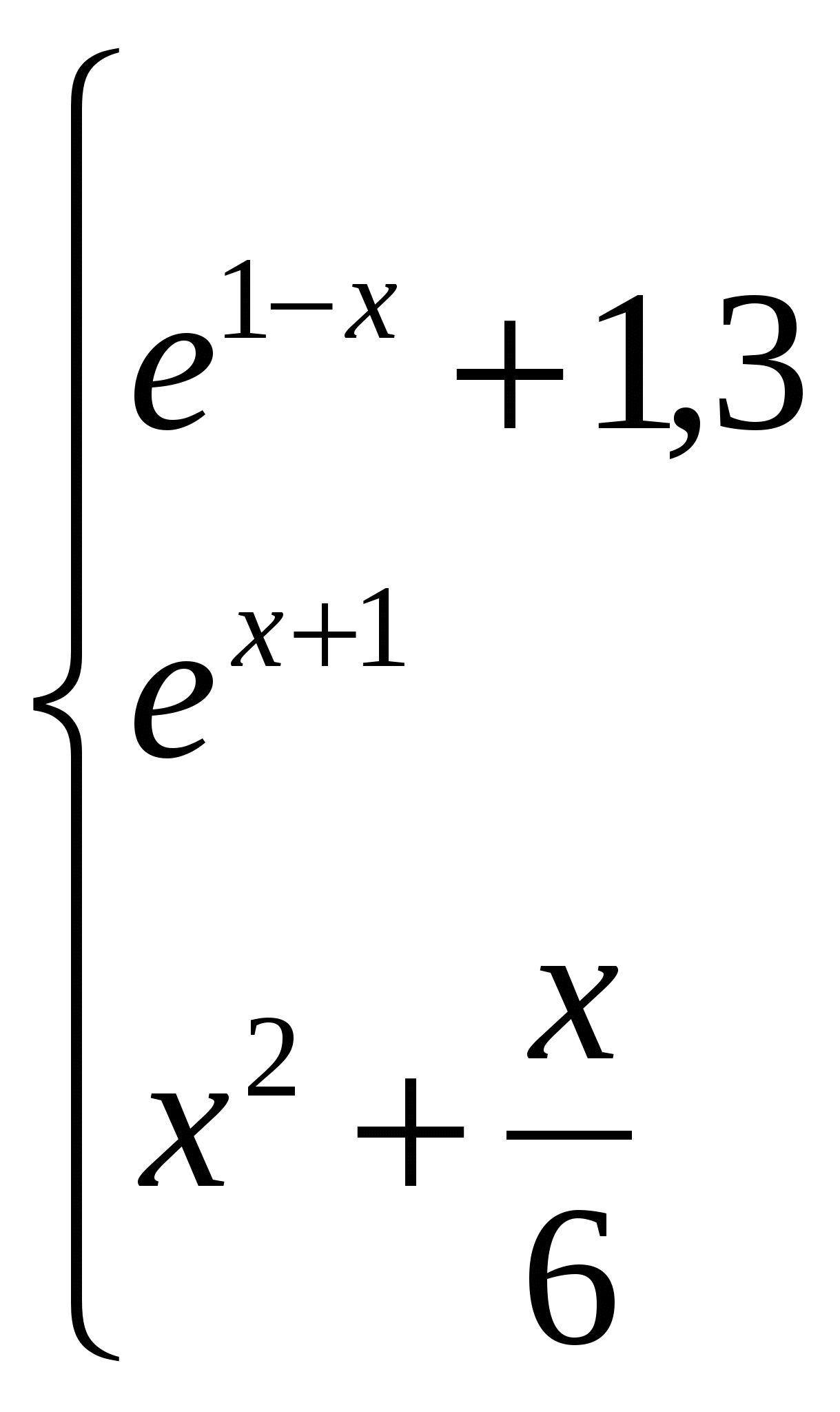
бчислити якщо x 1;
якщо -3 < x < 0;
інакше.
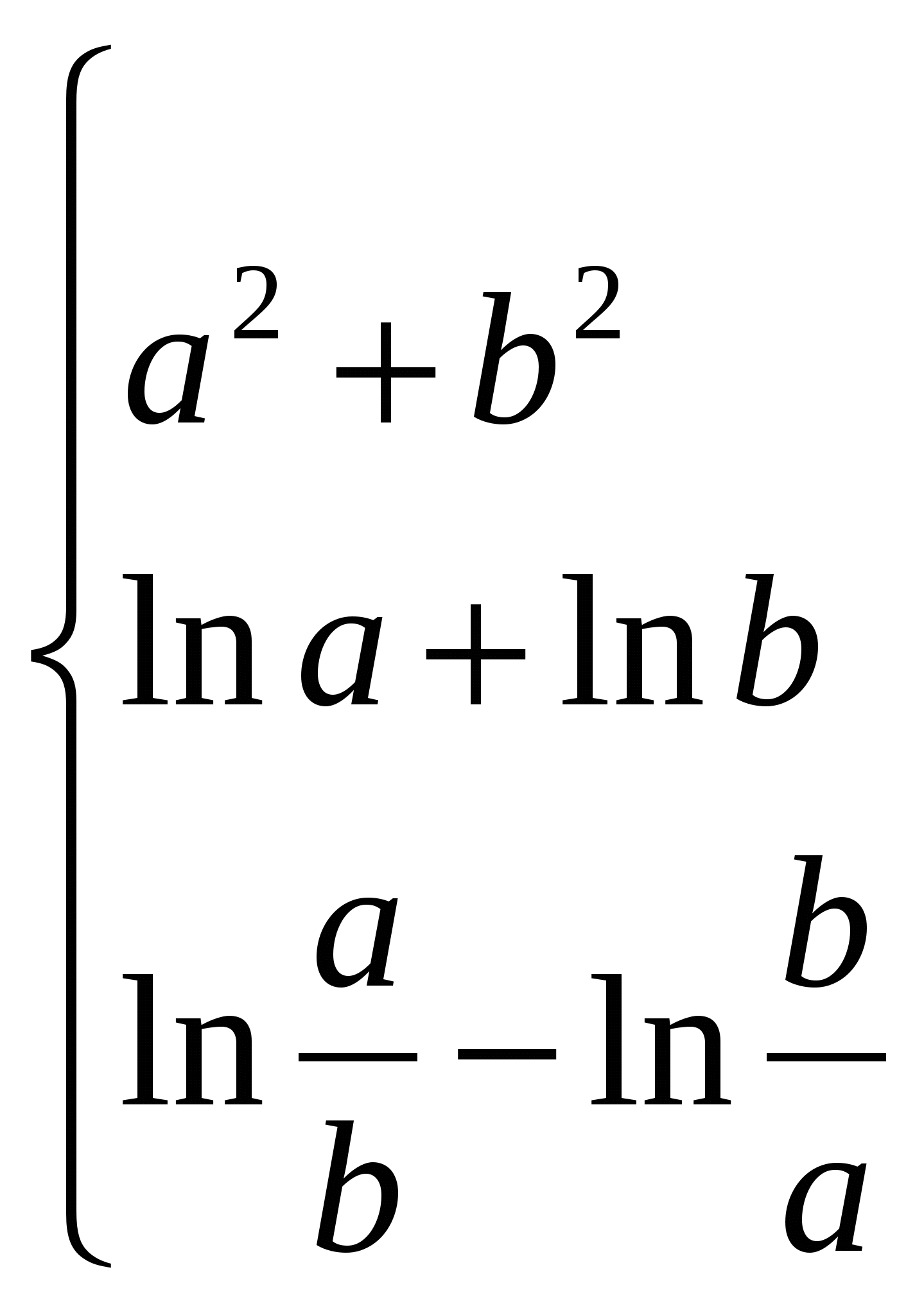
Обчислити якщо d=2;
якщо d=3;
інакше.
О
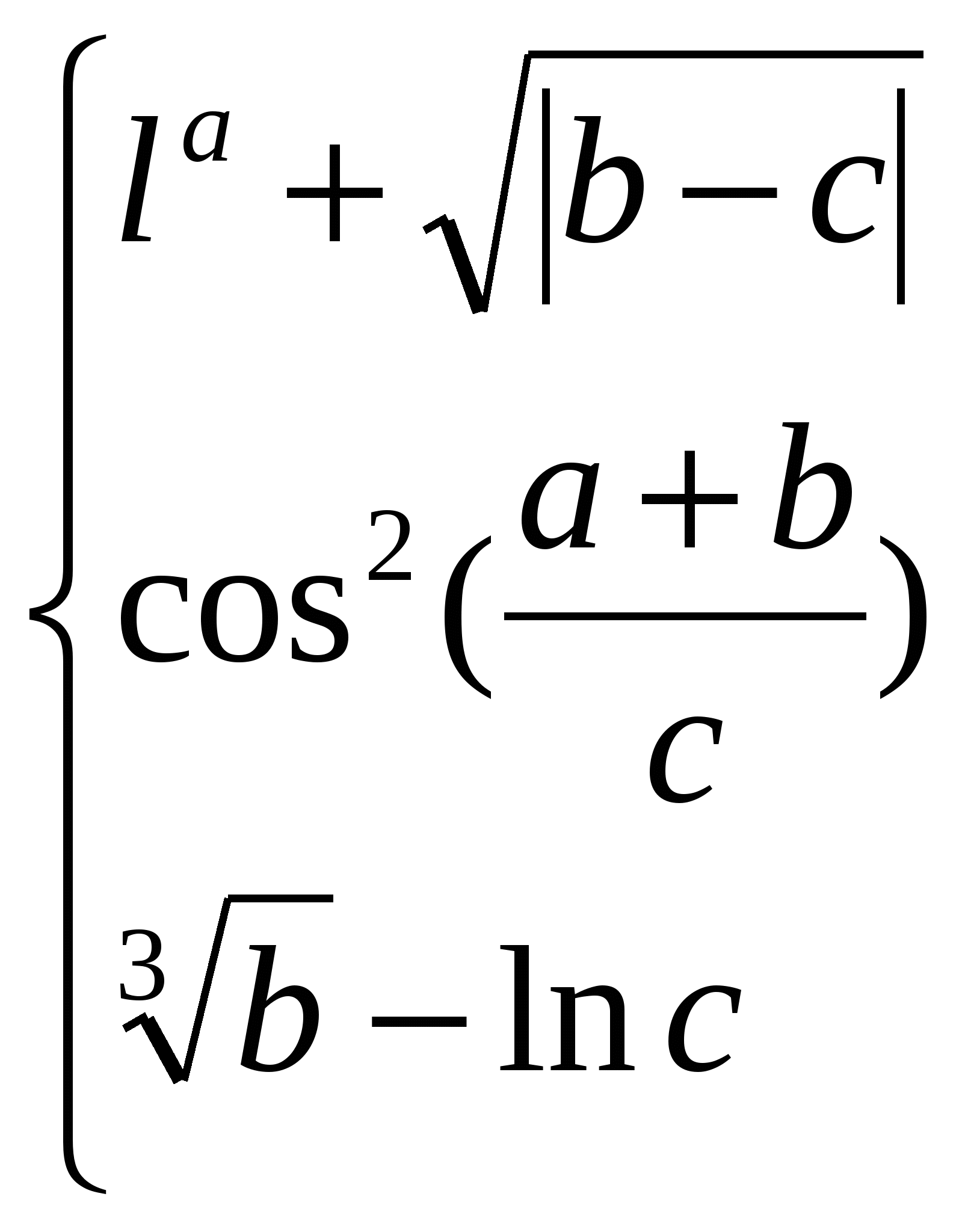
бчислити якщо a b;
якщо a = b;
інакше.
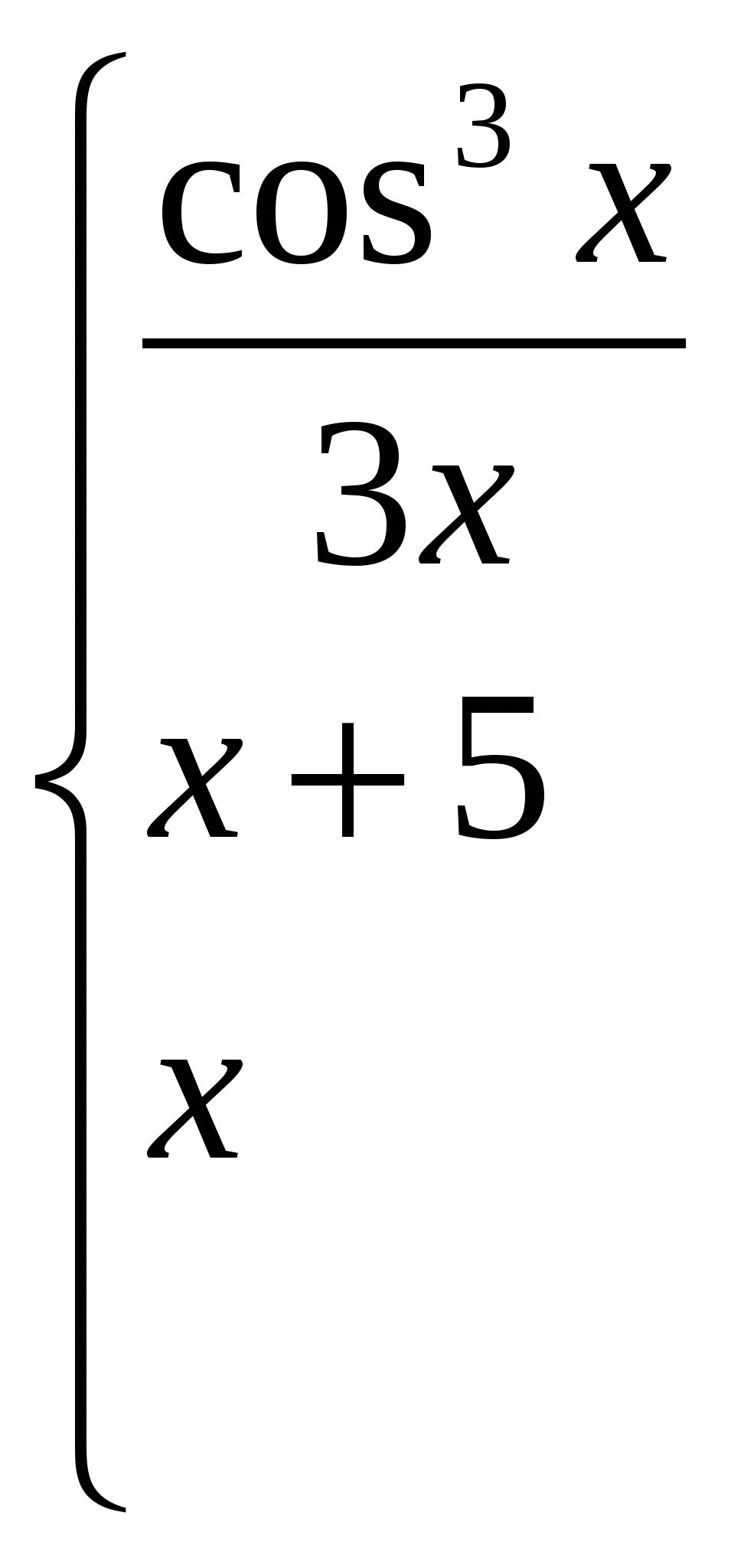
Обчислити якщо 2 x 3;
якщо -1 x 2;
інакше.
Визначити, чи належить точка А(x;y) колу, що задана рівнянням x2+(y+1)2=1.
Визначити, чи належить точка А(x;y) кривій, що задана рівнянням
y=1-x2.
Визначити, чи належить точка А(x;y) області, що задана нерівністю
(x-1)2+y2 2.
Визначити, чи належить точка А(x;y) області, що задана двома нерівностями
x2+y2 0,8; x2+y2 5.
Визначити, чи належить точка А(x;y) області, що задана нерівностями
x > 0; y < 0 і (x-1)2+(y+2)2 5,3.
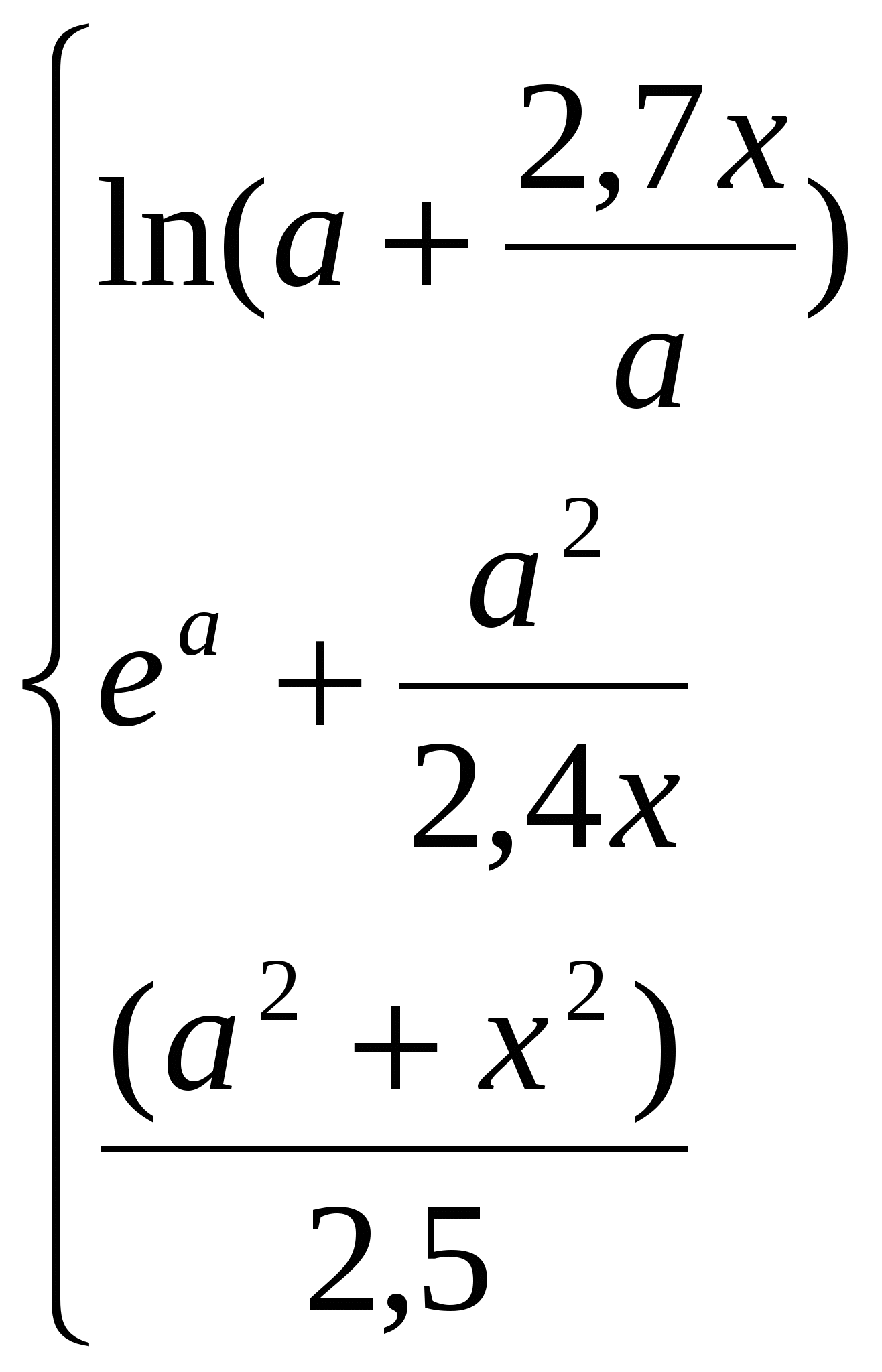
Обчислити якщо a 0 і x 3,7;
якщо a 0 і x 0;
інакше.
О
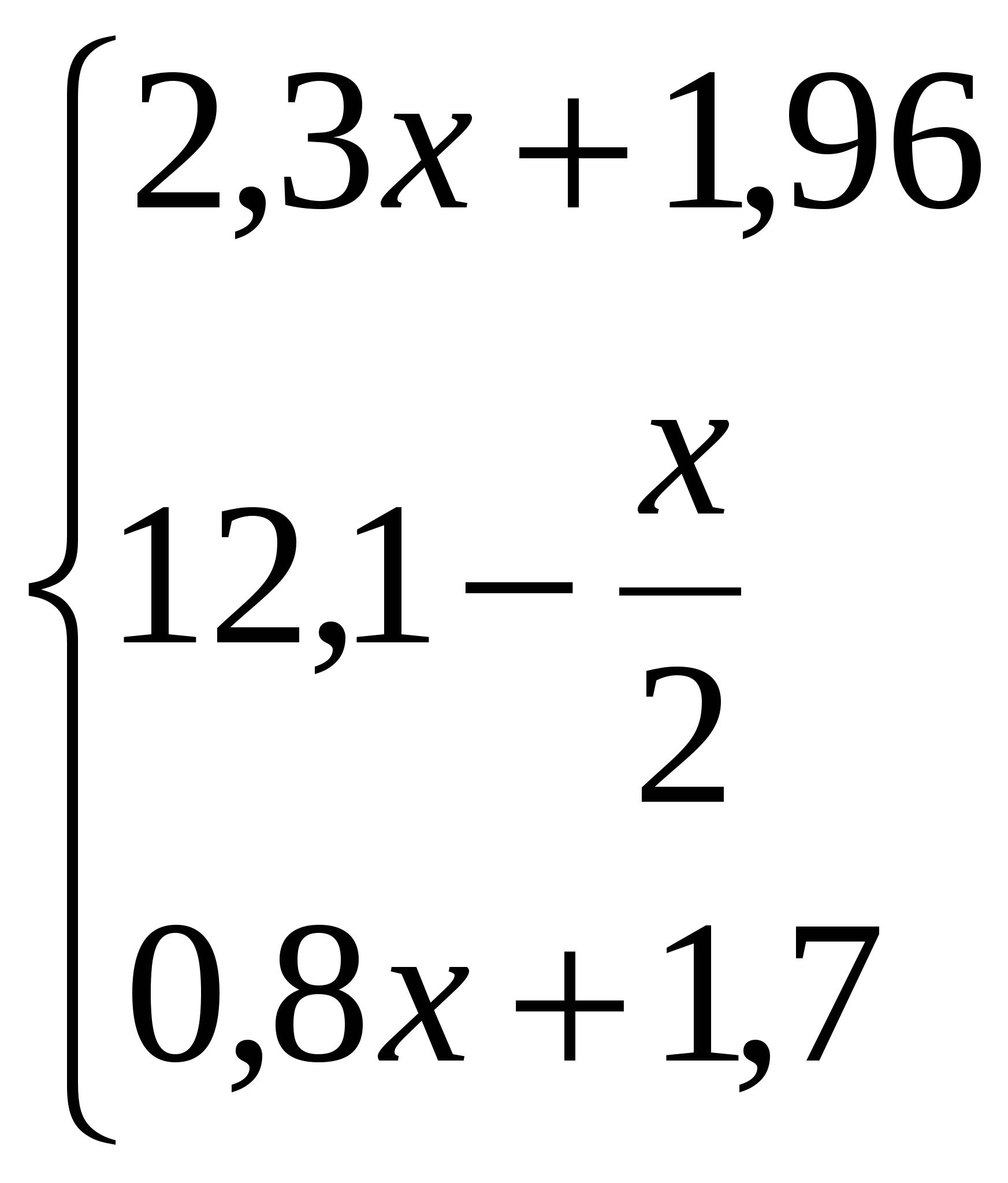
бчислити якщо e 0,6 і x 0;
якщо e 0,6 і x 0;
інакше.
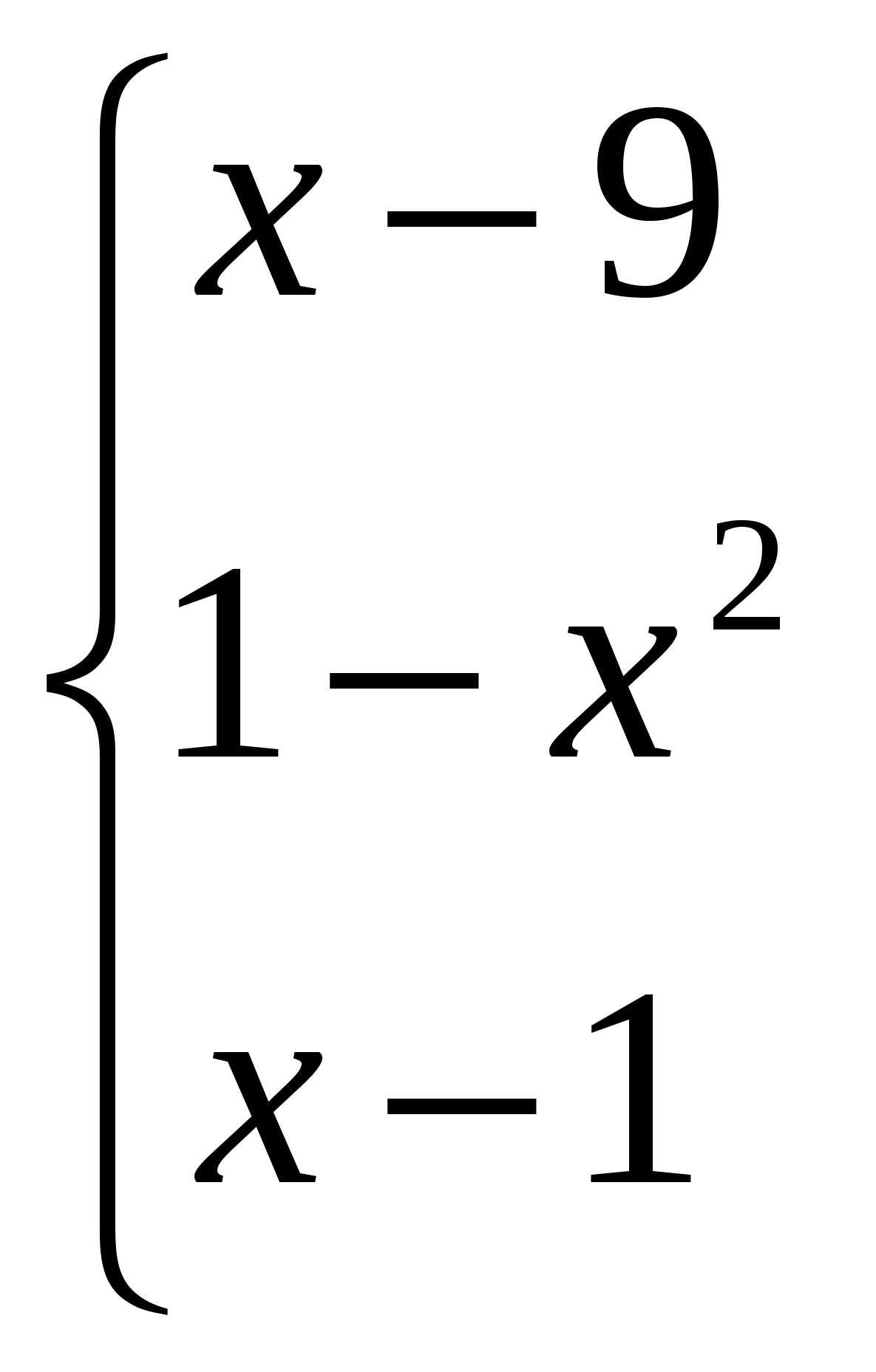
Обчислити якщо x -3;
якщо -3 x 2;
інакше.
Дано дійсні числа x, y, z. Визначити найбільше і найменше з цих чисел.
Контрольні запитання
Які правила побудови алгоритмів розгалуженої структури?
Які умовні позначення використовуються в алгоритмах розгалуженої структури?
Який вигляд мають оператори переходу?
Які умовні оператори використовуються в мові PASCAL?
Який загальний вигляд мають оператори вибору?
Які правила використання умовного оператора?
ЛАБОРАТОРНА РОБОТА 5
ПРОГРАМУВАННЯ АЛГОРИТМІВ ЦИКЛІЧНОЇ СТРУКТУРИ. ОПЕРАТОРИ ЦИКЛУ WHILE І REPEAT
Мета роботи: отримання практичних навиків розробки алгоритмів циклічної структури та розробки програм, що реалізують ці алгоритми.
Робоче завдання
Скласти схему алгоритму і розробити програму, що виконують такі дії:
виведення заголовка лабораторної роботи, у якому вказується найменування лабораторної роботи, її номер, варіант індивідуального завдання, прізвище студента та навчальна група;
введення початкових даних лабораторної роботи;
здійснення обчислень у циклі за введеними даними із використанням операторів циклу WHILE І REPEAT;
виведення початкових даних і результатів обчислень лабораторної роботи;
Варіанти індивідуальних завдань для виконання лабораторної роботи
Д
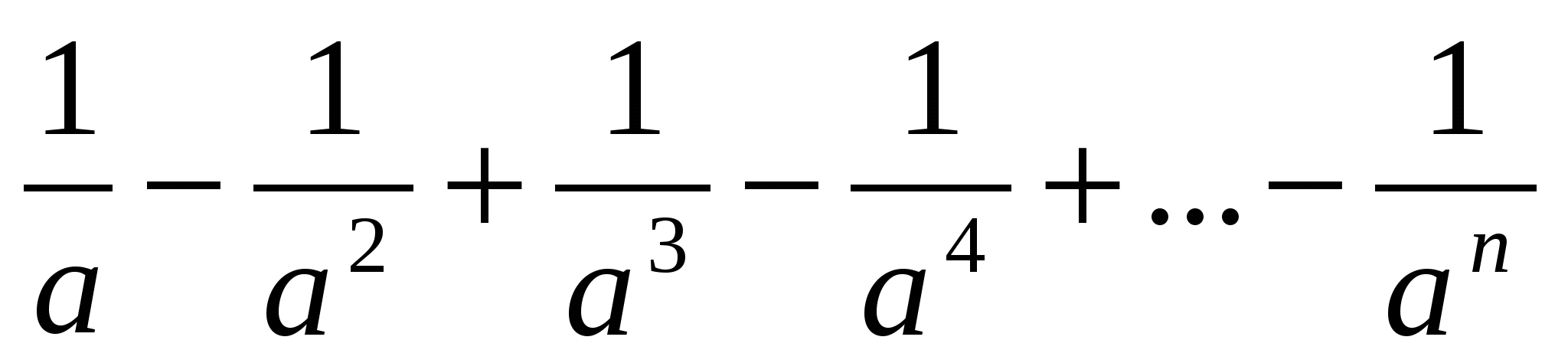
ано натуральне число n і дійсне a. Обчислити
Д
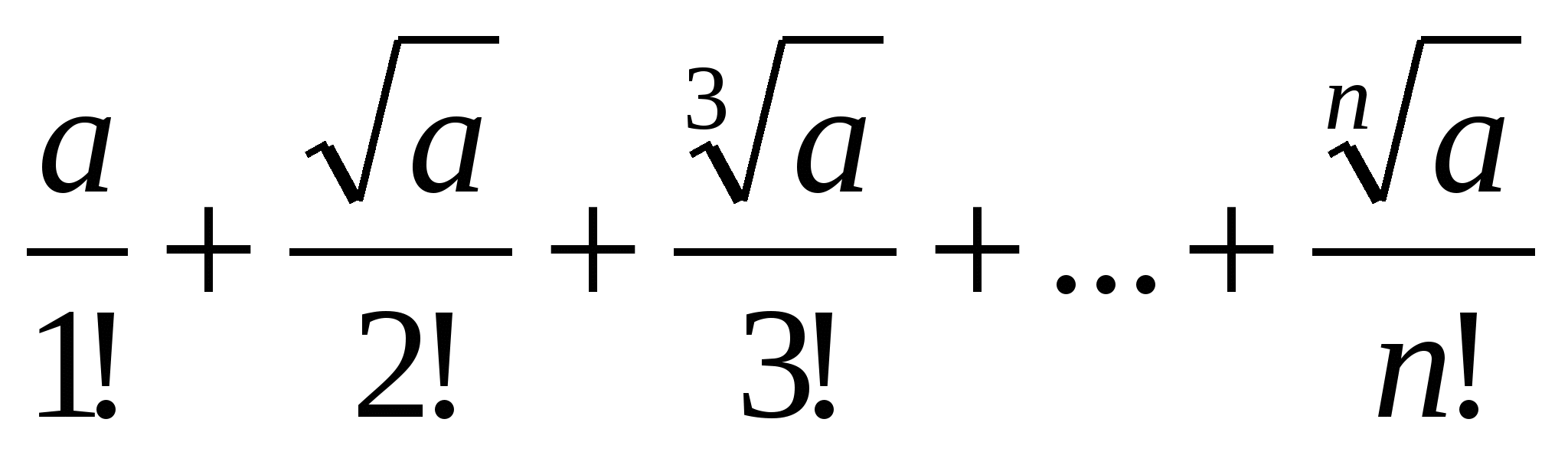
ано натуральне число n і дійсне a. Обчислити
Д
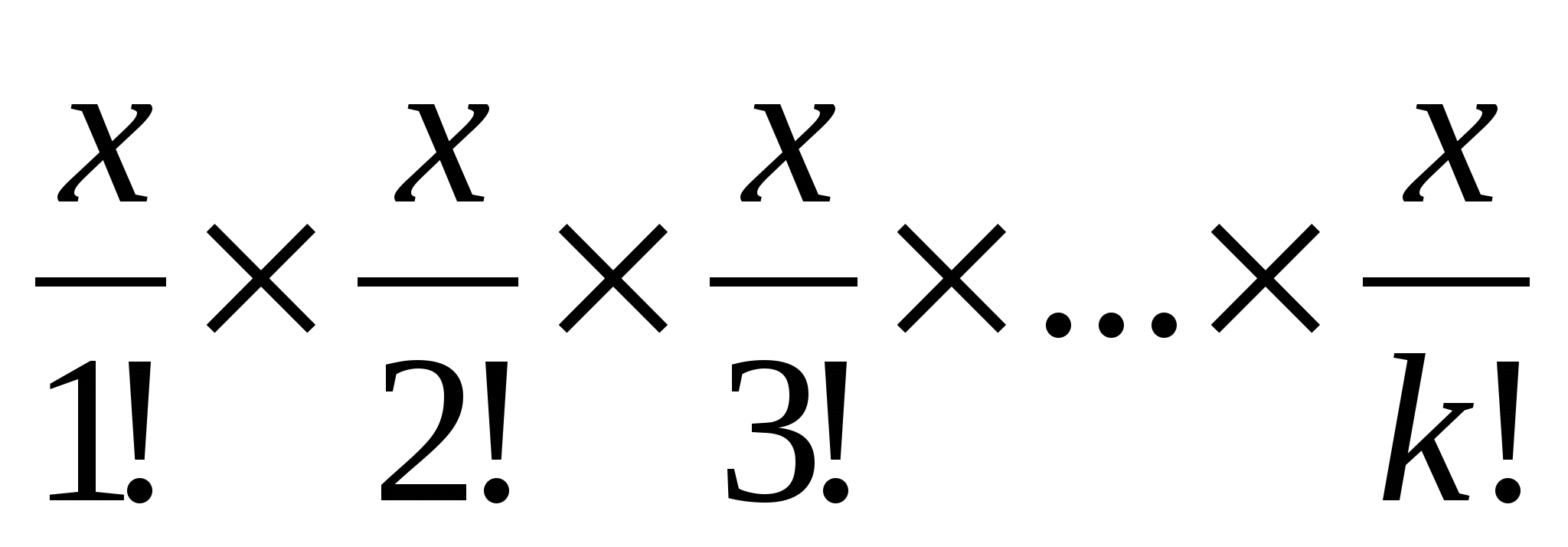
ано натуральне число k і дійсне x. Обчислити
Нехай а0=а1=1; аi=аi-2+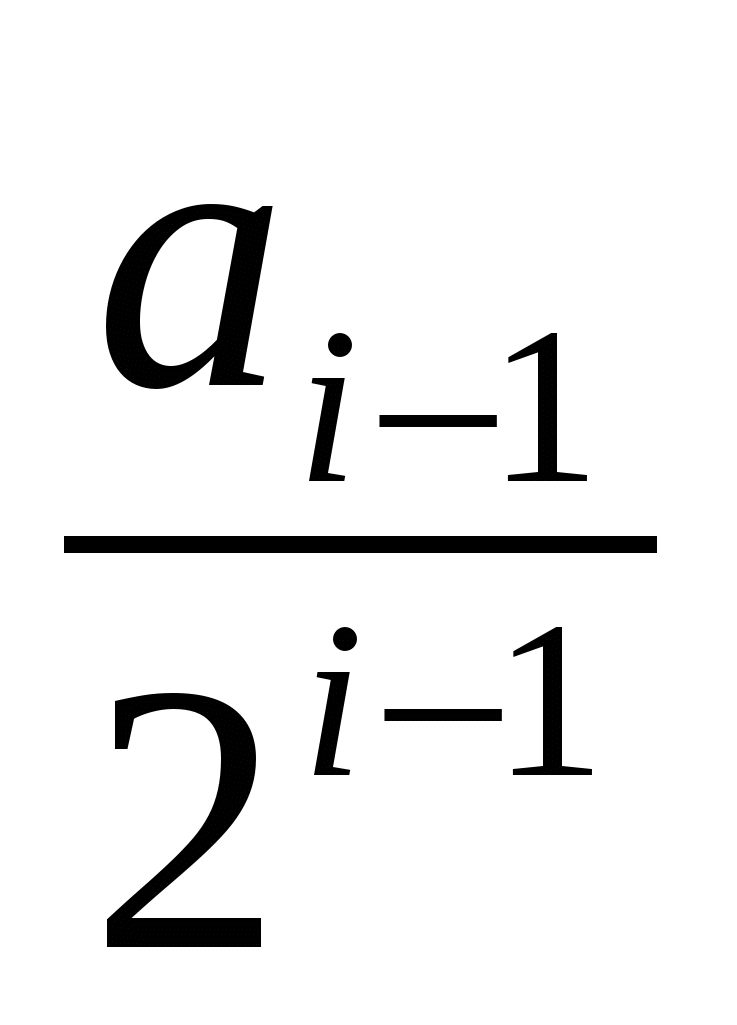 , i=2,3,4,5. Знайти добуток а0×а1×а2×…×а5 , i=2,3,4,5. Знайти добуток а0×а1×а2×…×а5
Дано натуральне число n і дійсне x. Обчислити sin(x)×sin2(x)×…×sinn(x)
Дано натуральне число n і дійсне x. Обчислити sin(x)×sin(x2)×sin(x3)×…×sin(xn)
Дано натуральне число m і дійсне x. Обчислити sin(x)+sin(sin(x)+…+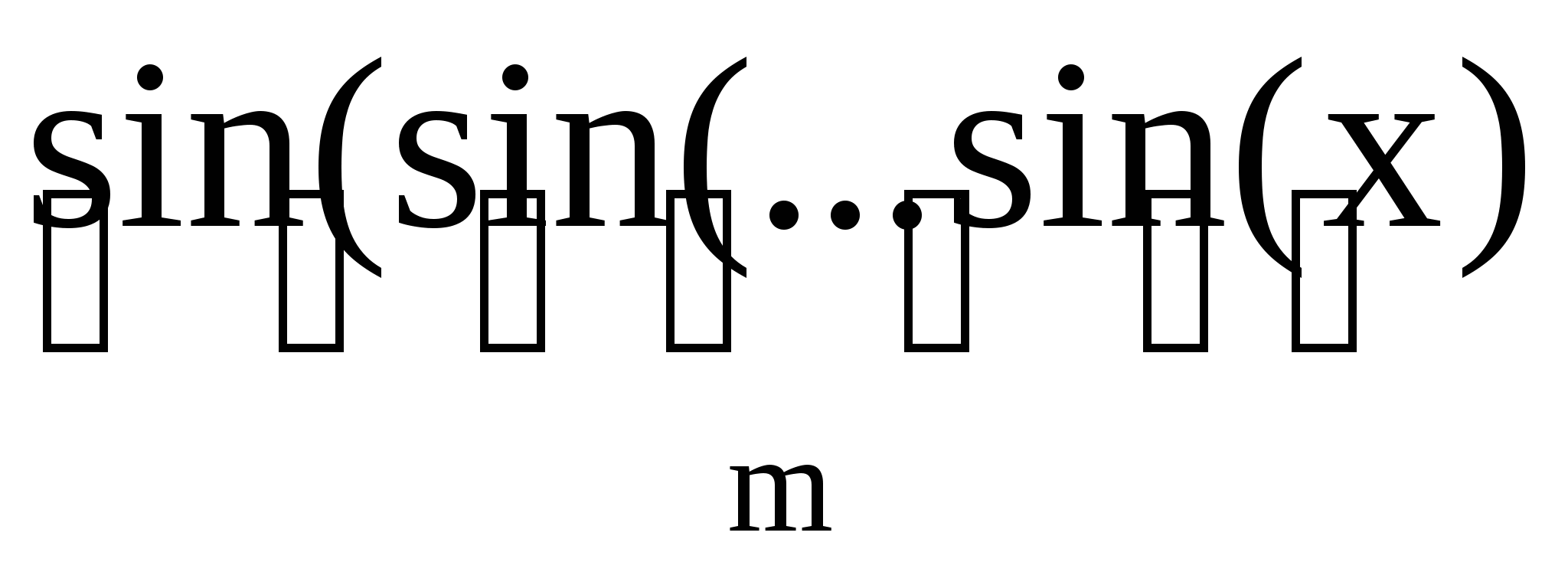
Дано дійсне число a. Знайти серед чисел 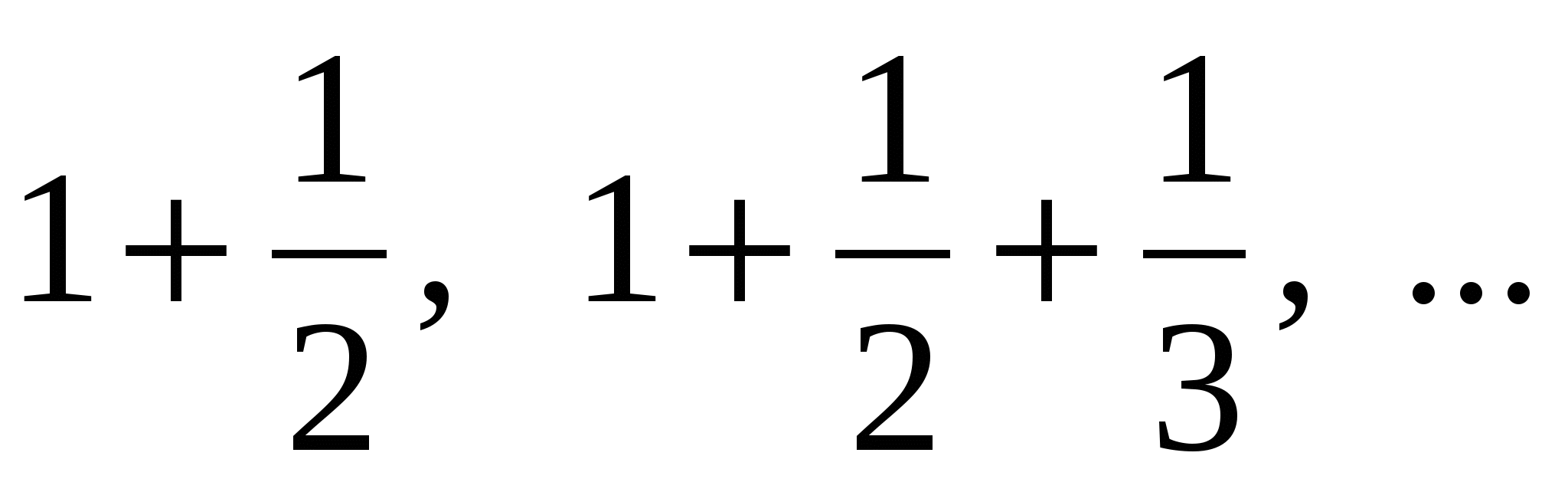 перше, що стане більшим числаa. перше, що стане більшим числаa.
Д
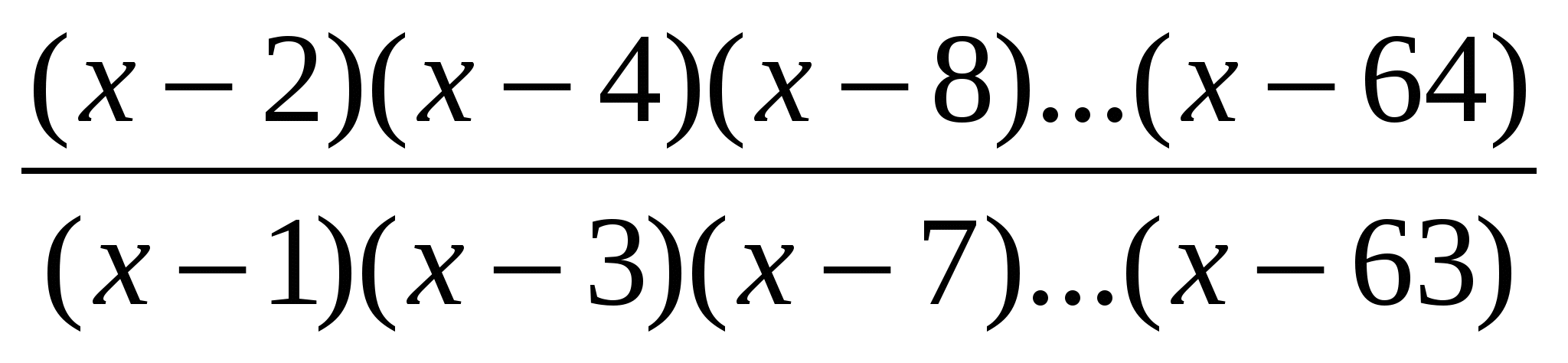
ано дійсне число b. Знайти таке найменше m, що 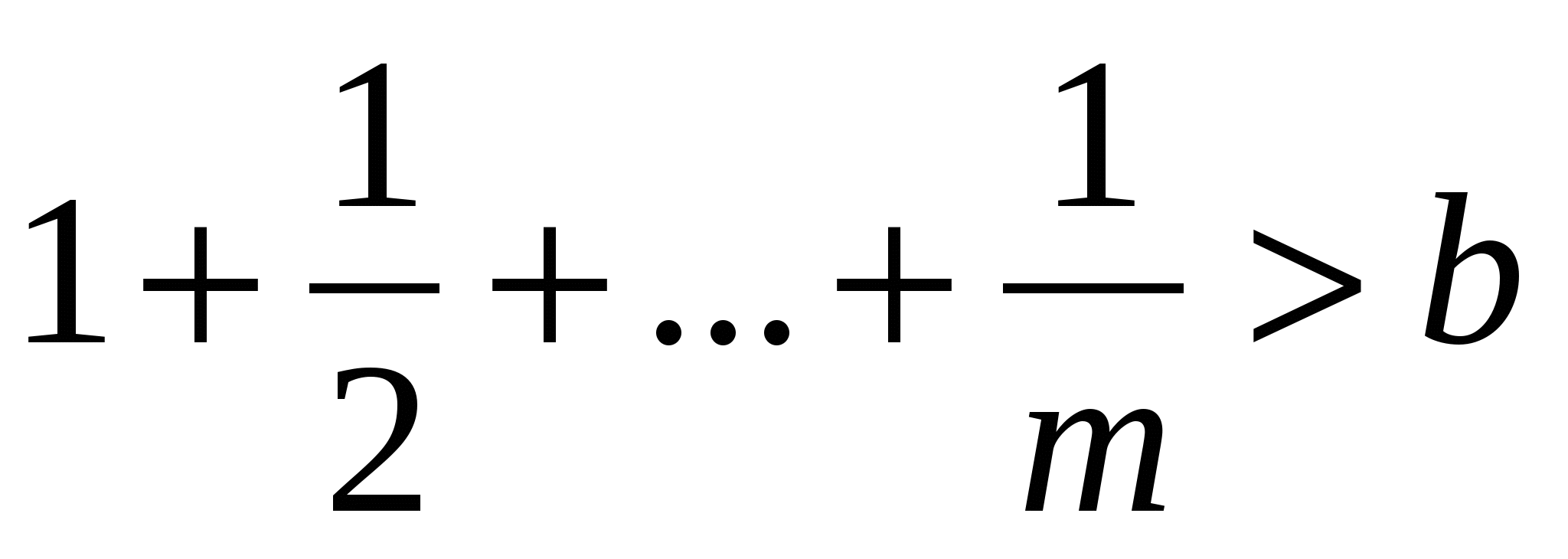
Д

ано дійсне число x. Обчислити
Д
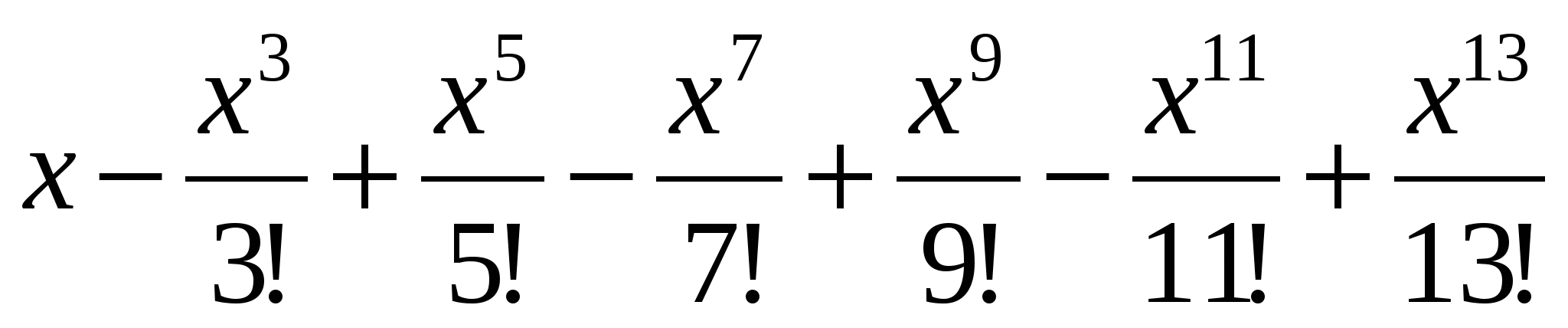
ано натуральне число b і дійсні x та a. Обчислити
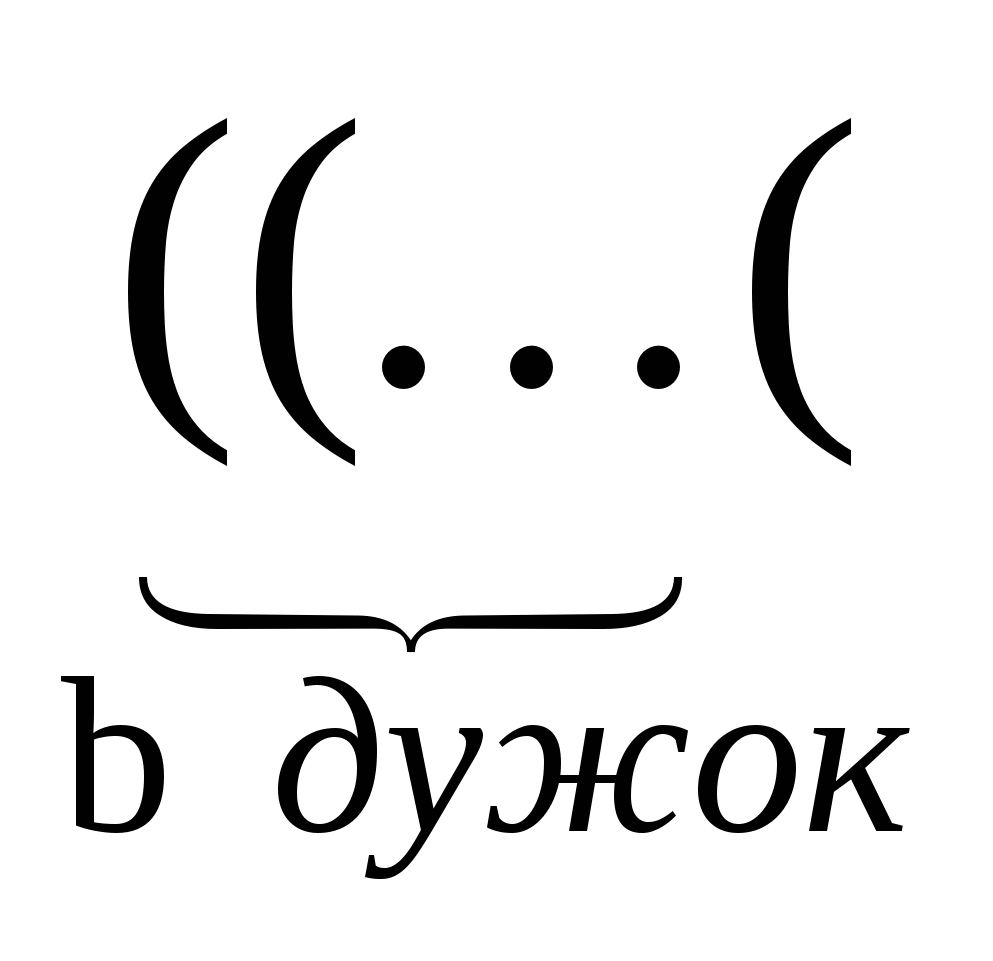 x-a)2+a)2…+a)2+a x-a)2+a)2…+a)2+a
Дано дійсне число x. Обчислити
Обчислити (1+sin( 0,1))(1+sin(0,2))…(1+sin(1,0))
Дано натуральне число a і дійсне b. Обчислити b(b+1)(b+2)…(b+a-1)
Д
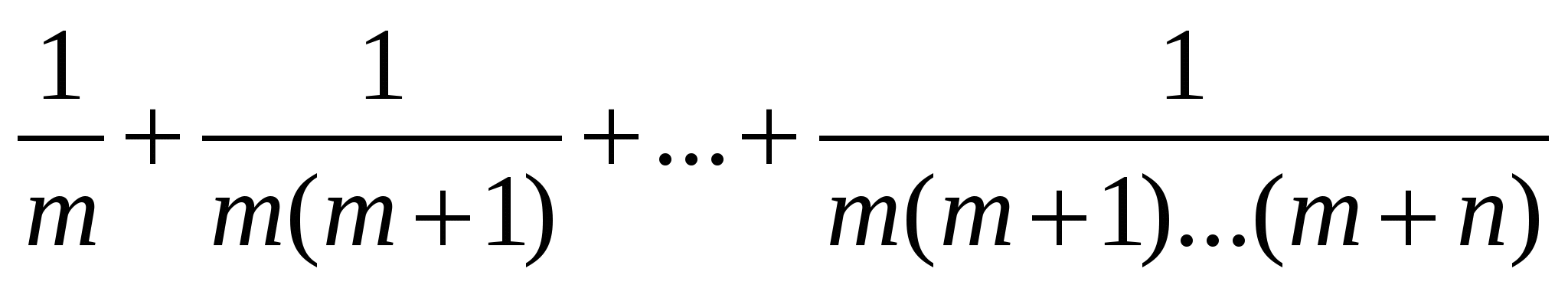
ано натуральне число n і дійсне m.
Обчислити
Дано натуральне число a. Обчислити a2!
Д
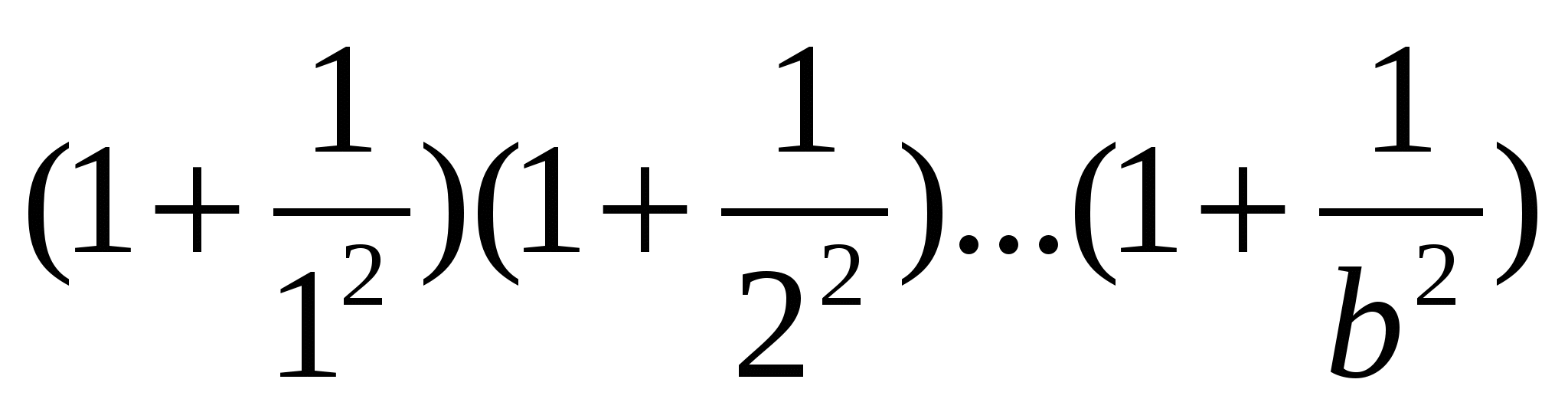
ано натуральне число b. Обчислити
Дано натуральне число C. Обчислити 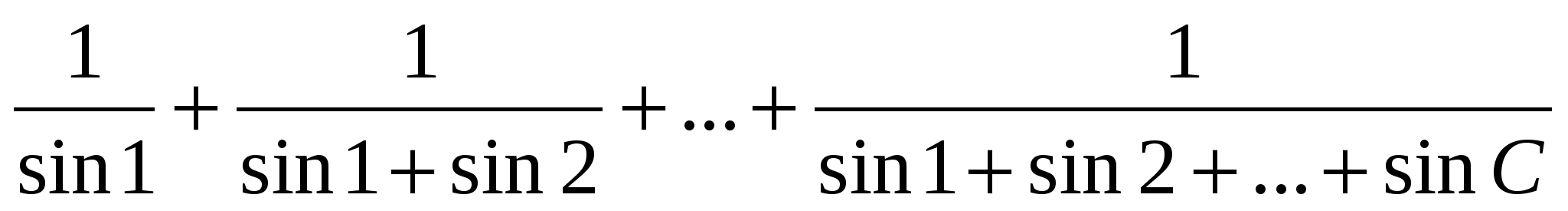
Д
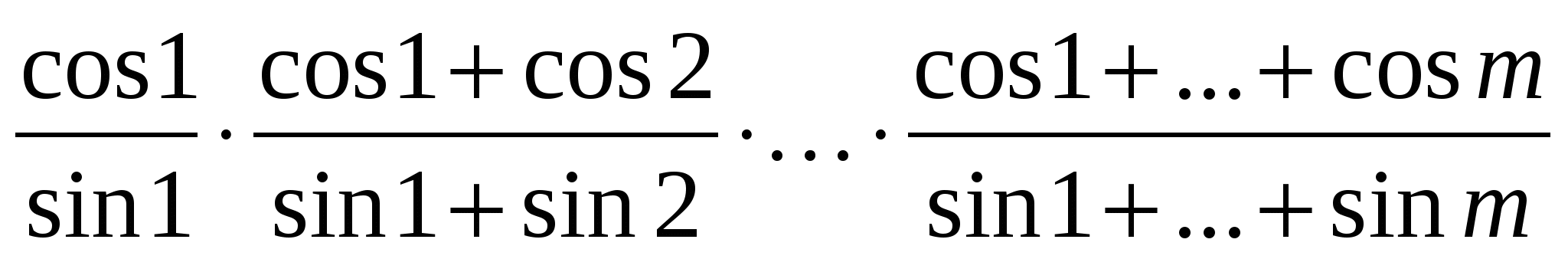
ано натуральне число n. Обчислити 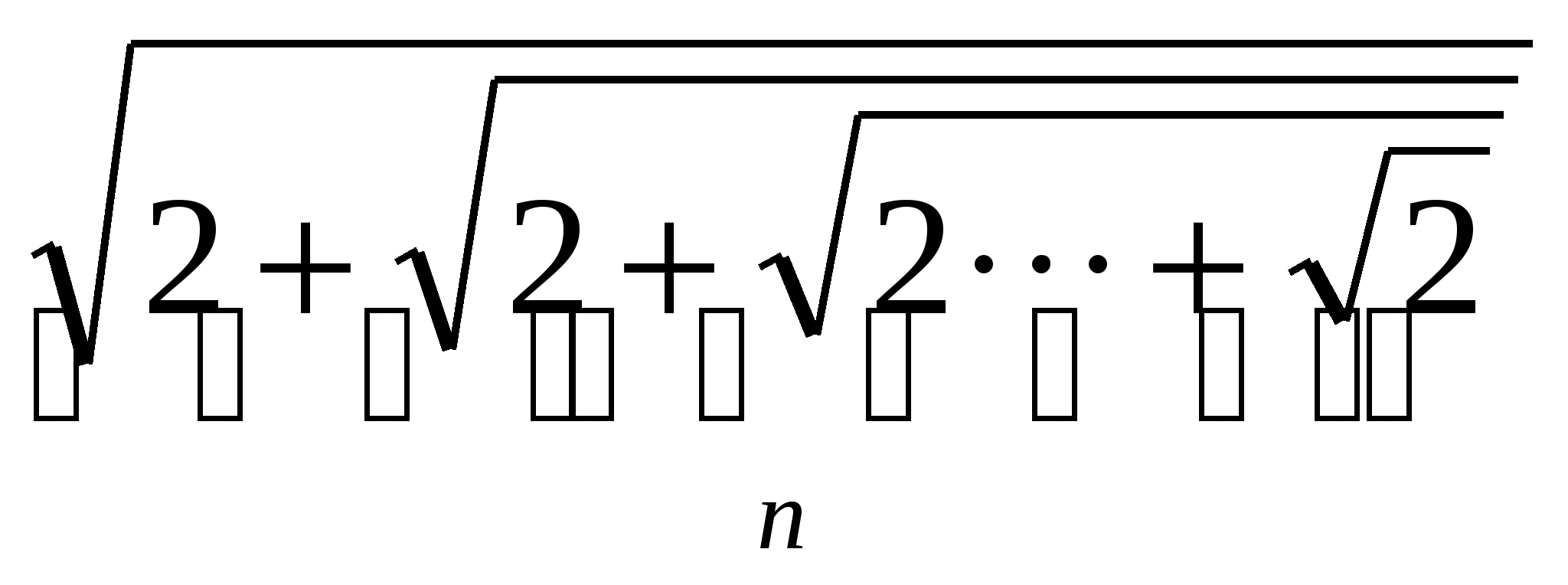
Дано натуральне число m.
Обчислити
Д
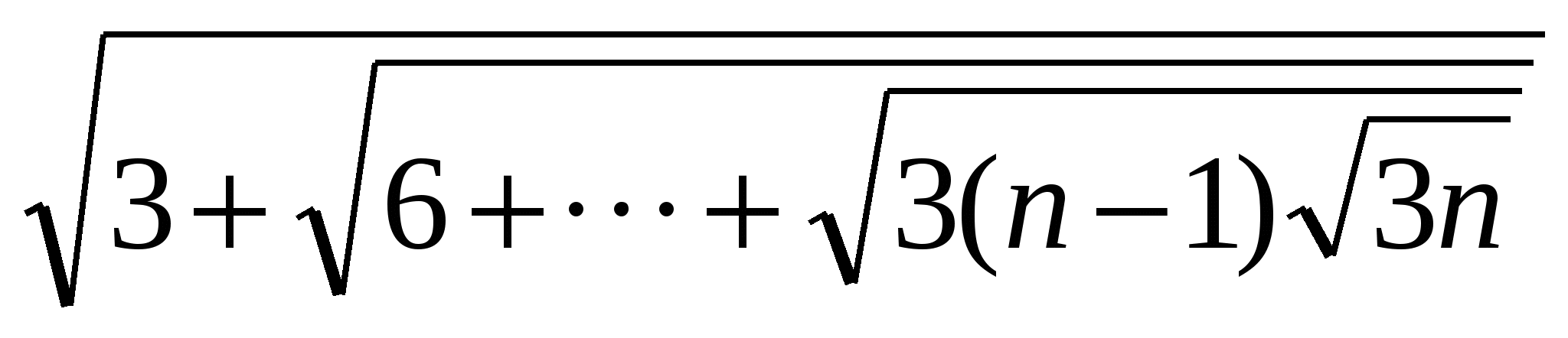
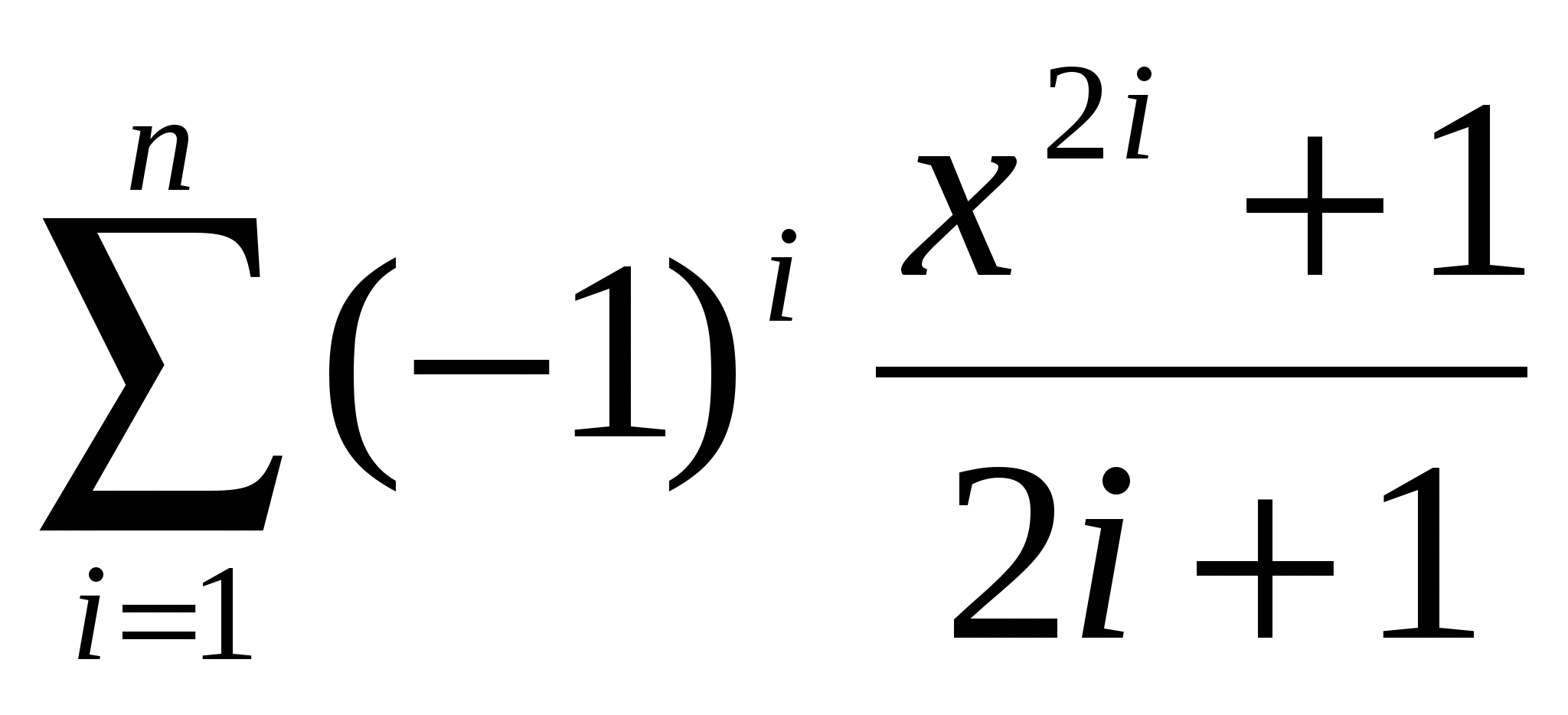 ано натуральне число n. Обчислити ано натуральне число n. Обчислити
Дано натуральне число n і дійсне x. Обчислити
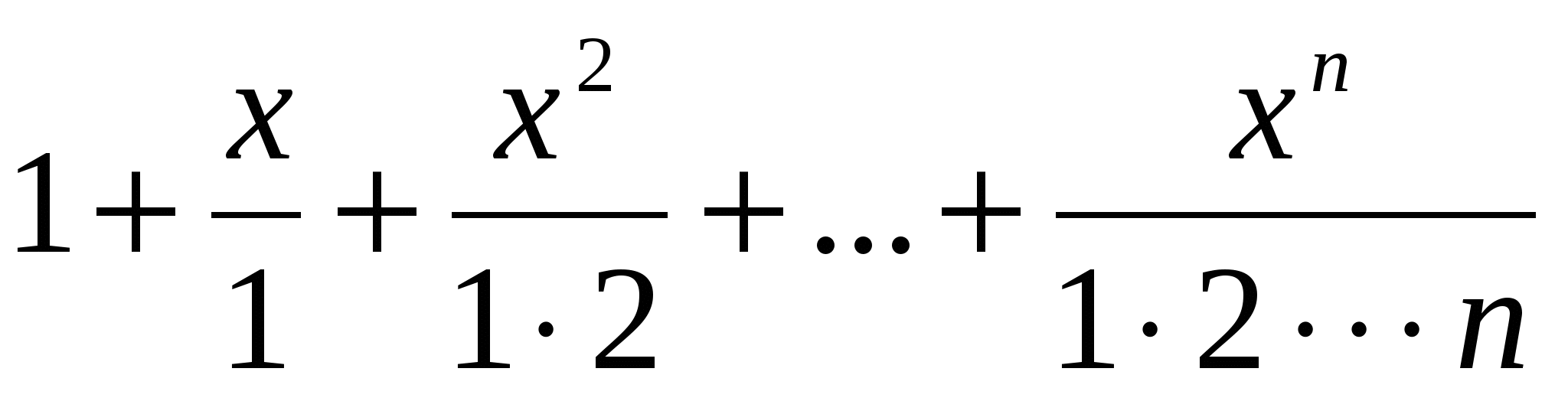
Дано натуральне число n і дійсне x.
Обчислити
Д
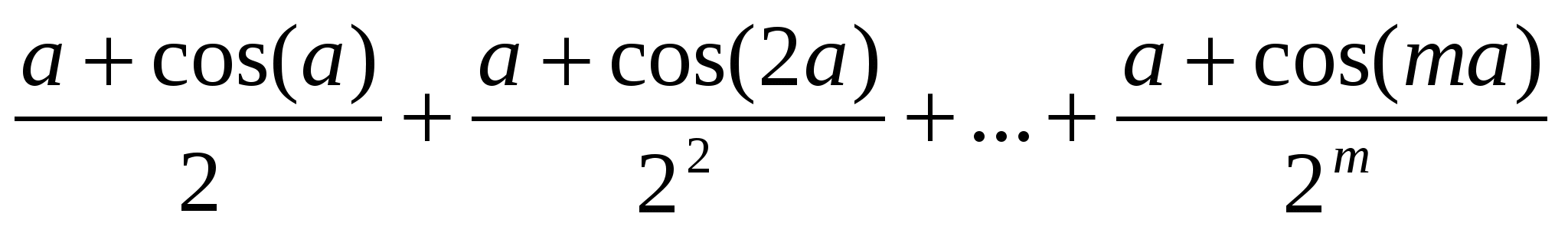
ано натуральне число m і дійсне a.
Обчислити
Дано натуральне число n. Обчислити 1×2+2×3×4+…+n(n+1)…2n
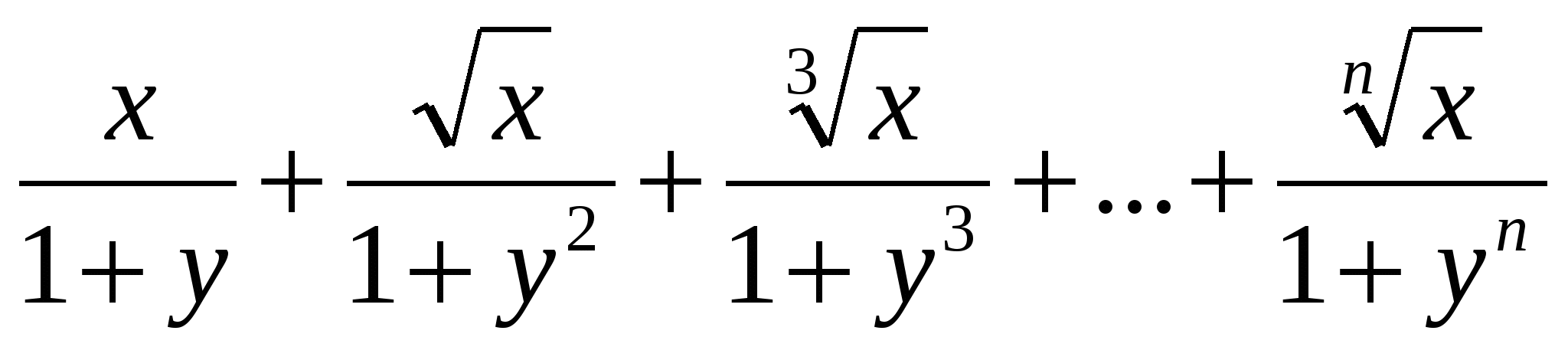
Дано натуральне число n і дійсні x та y.
Обчислити
Д
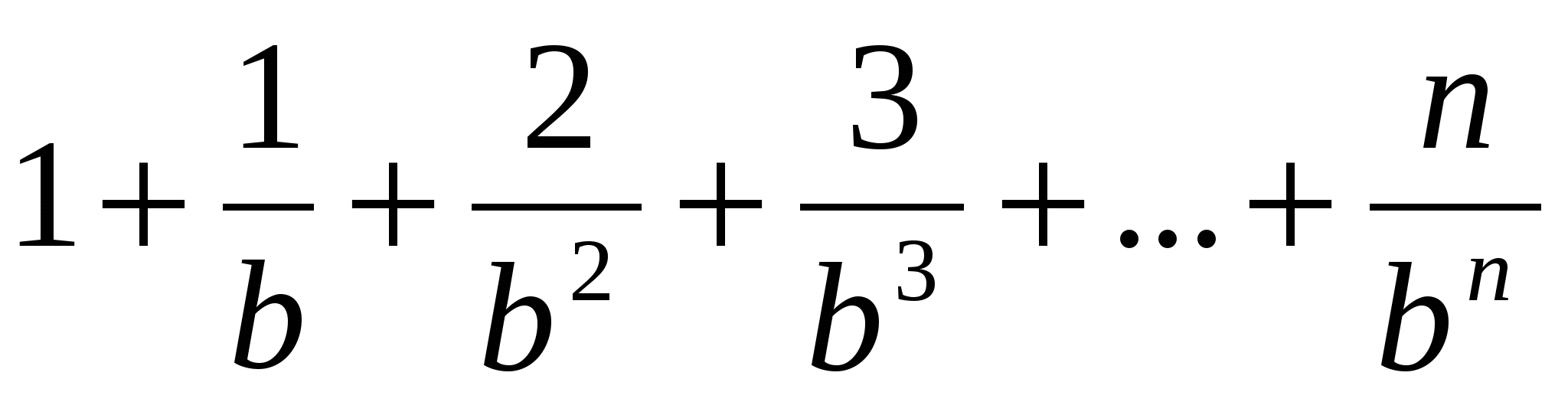
ано натуральне число n і дійсне b, (b1).
Обчислити
Д
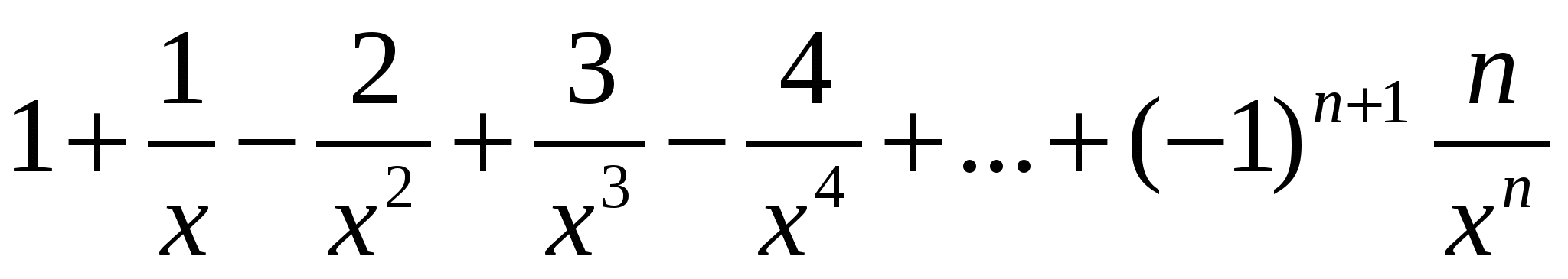
ано натуральне число m, (m 1) і дійсне a, (0 a 1).
Обчислити
Д
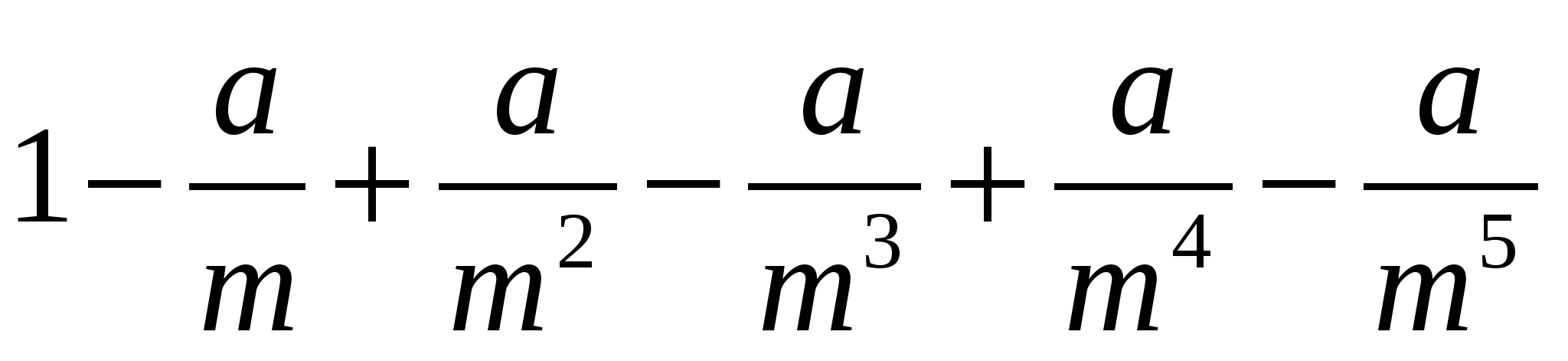
ано натуральне число n і дійсне x (x 1).
Обчислити
Д
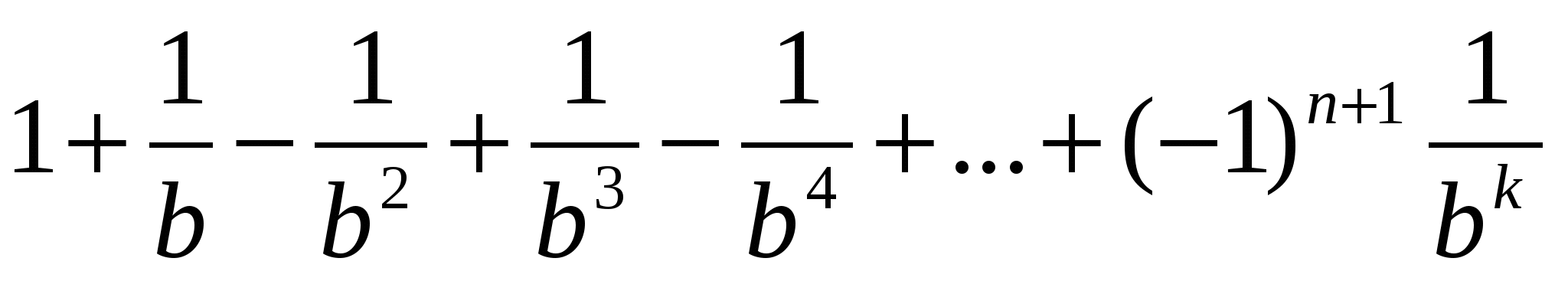
ано натуральне число k і дійсне b, (b 1).
Обчислити
Контрольні запитання
Що таке цикл? Які переваги використання циклів в алгоритмах?
Як організувати цикл?
Як організувати цикл з наперед невідомою кількістю повторень?
Що таке „ітераційний” цикл?
Який вигляд має оператор циклу з передумовою?
Як представляється оператор циклу з постумовою?
Як організувати цикл із дробовим кроком?
Як організувати „вкладені” цикли?
Як представити схему алгоритму обчислення суми?
Який вигляд має схема алгоритму обчислення добутку?
Який вигляд має алгоритм пошуку найбільшого елемента масиву?
Який вигляд має схема алгоритму пошуку найменшого елемента масиву?
ЛАБОРАТОРНА РОБОТА 6
ПРОГРАМУВАННЯ АЛГОРИТМІВ ЦИКЛІЧНОЇ СТРУКТУРИ КЛАСИЧНИМ МЕТОДОМ (ОПЕРАТОРИ IF, GOTO) ТА ЗА ДОПОМОГОЮ ОПЕРАТОРА FOR
Мета роботи: отримання практичних навиків розробки алгоритмів циклічної структури та розробки програм, що реалізують ці алгоритми.
Робоче завдання
Скласти схему алгоритму і розробити програму, що виконують такі дії:
виведення заголовка лабораторної роботи, у якому вказується найменування лабораторної роботи, її номер, варіант індивідуального завдання, прізвище студента та навчальна група;
введення початкових даних лабораторної роботи;
здійснення обчислень у циклі за введеними вихідним даним класичним способом (за допомогою операторів IF і GOTO) та з використанням оператора циклу FOR;
виведення початкових даних і результатів обчислень лабораторної роботи.
Варіанти індивідуальних завдань для виконання другої частини лабораторної роботи
Обчислити 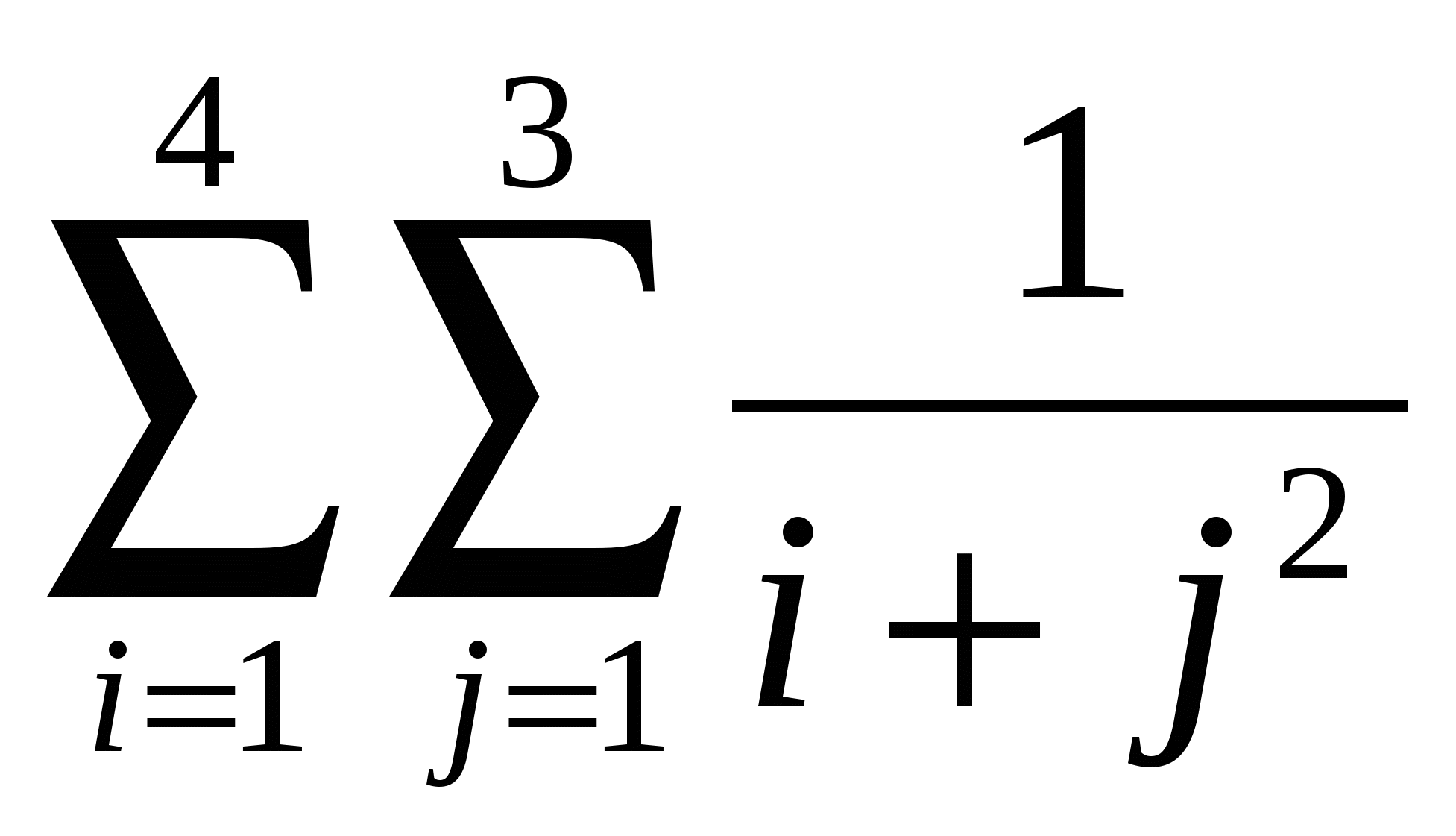 . .
Обчислити 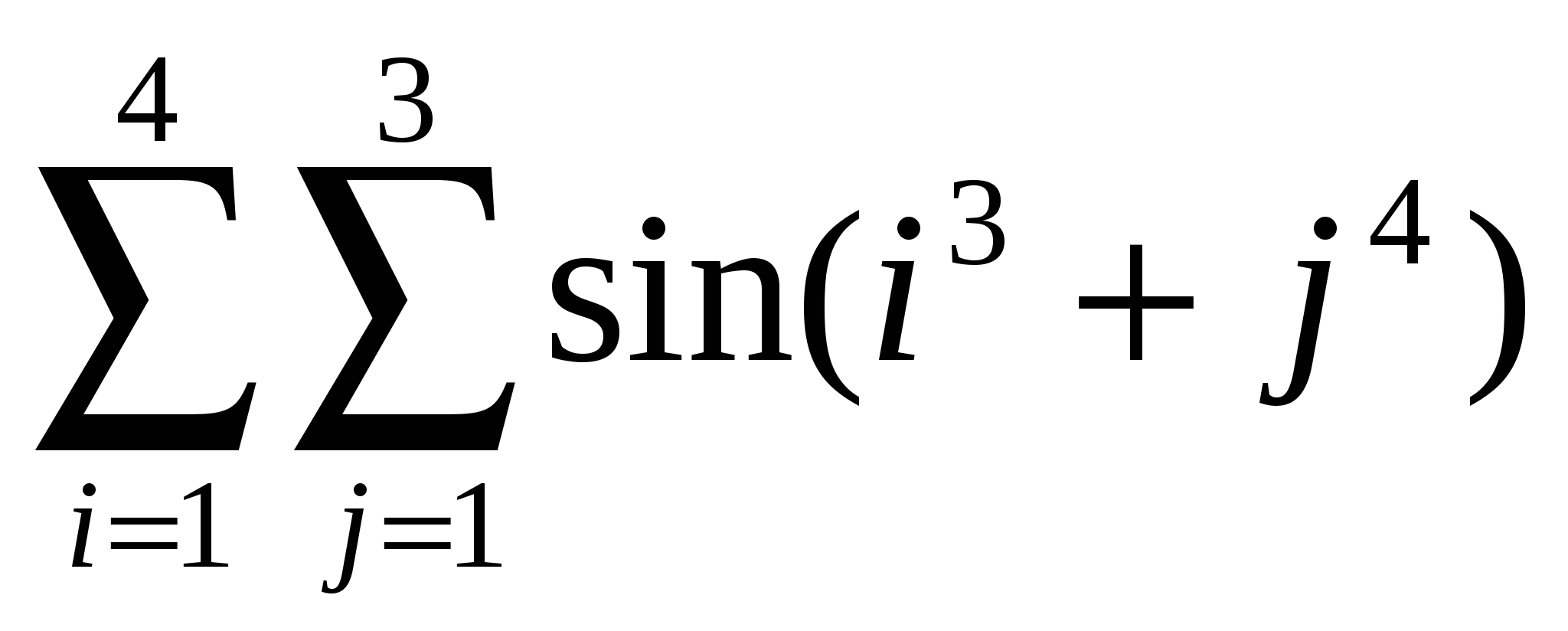 . .
Обчислити 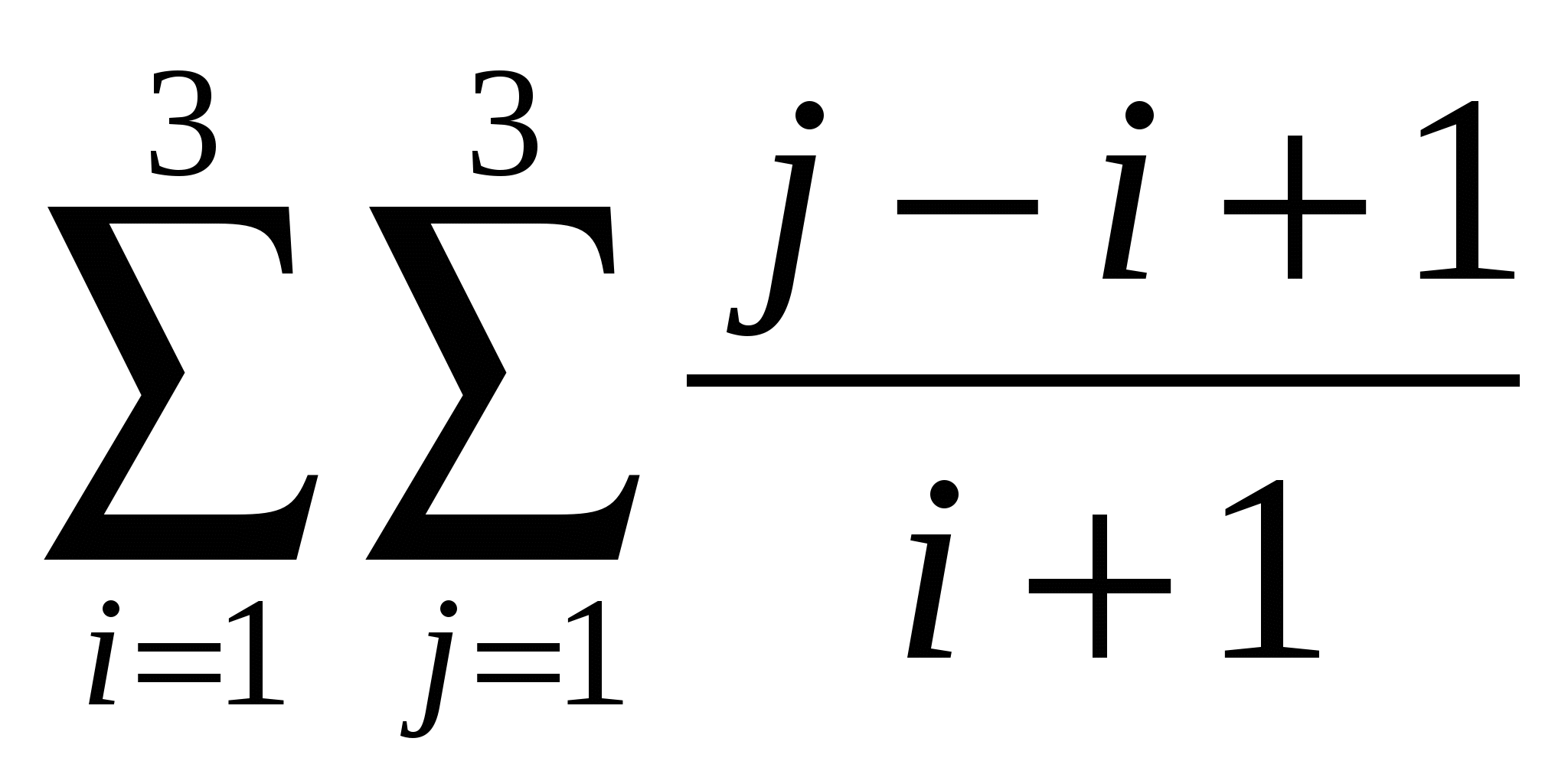 . .
Обчислити 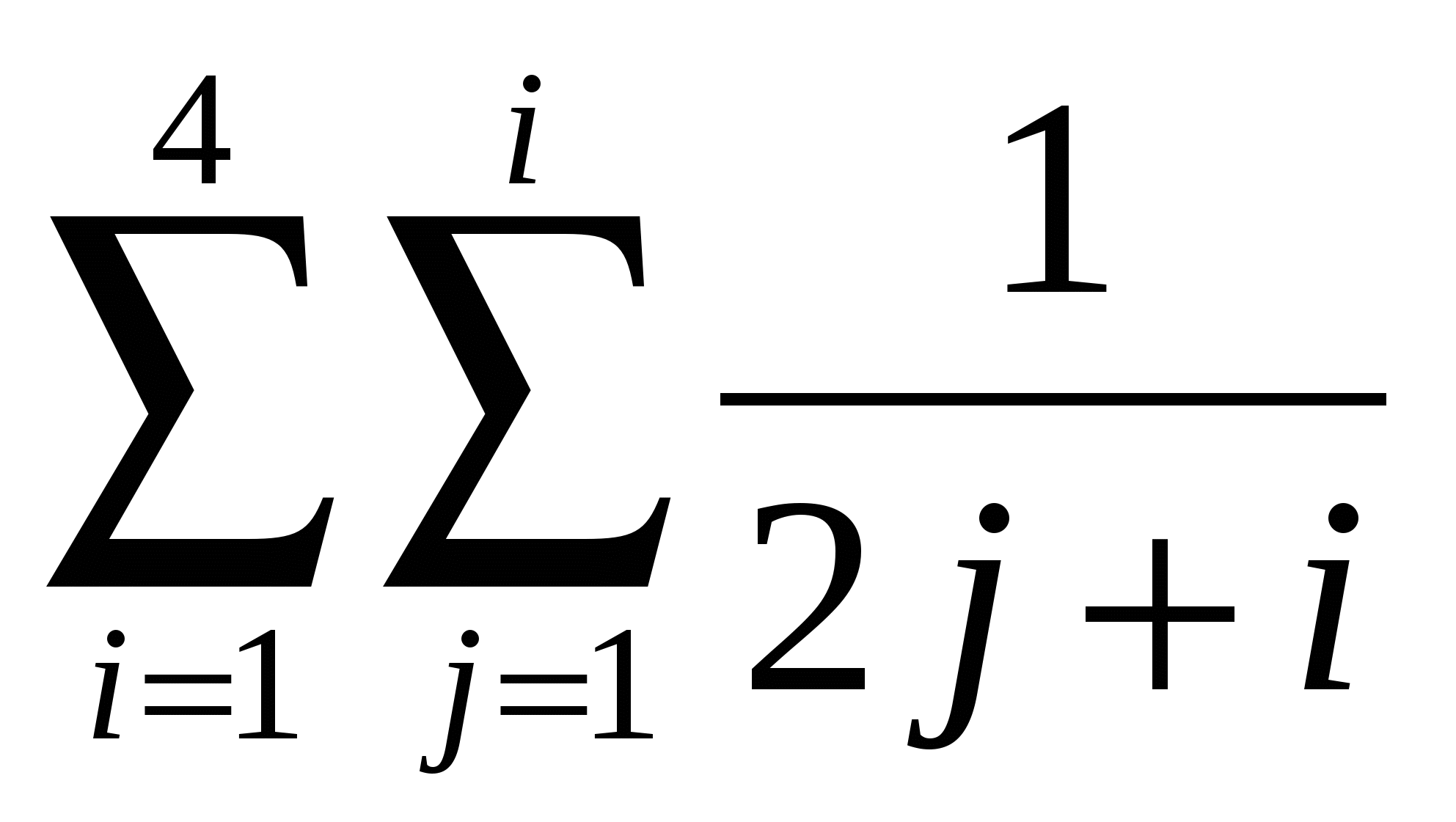 . .
Обчислити 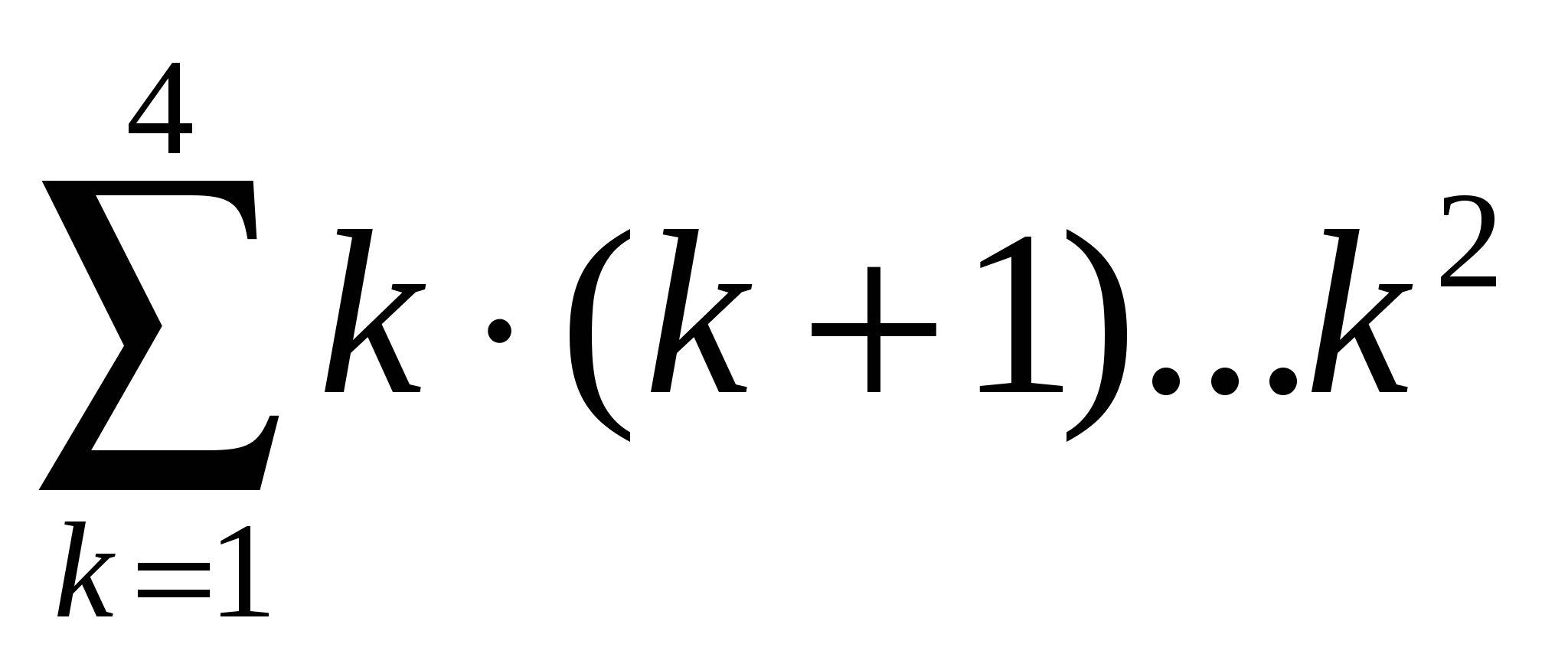 . .
Обчислити 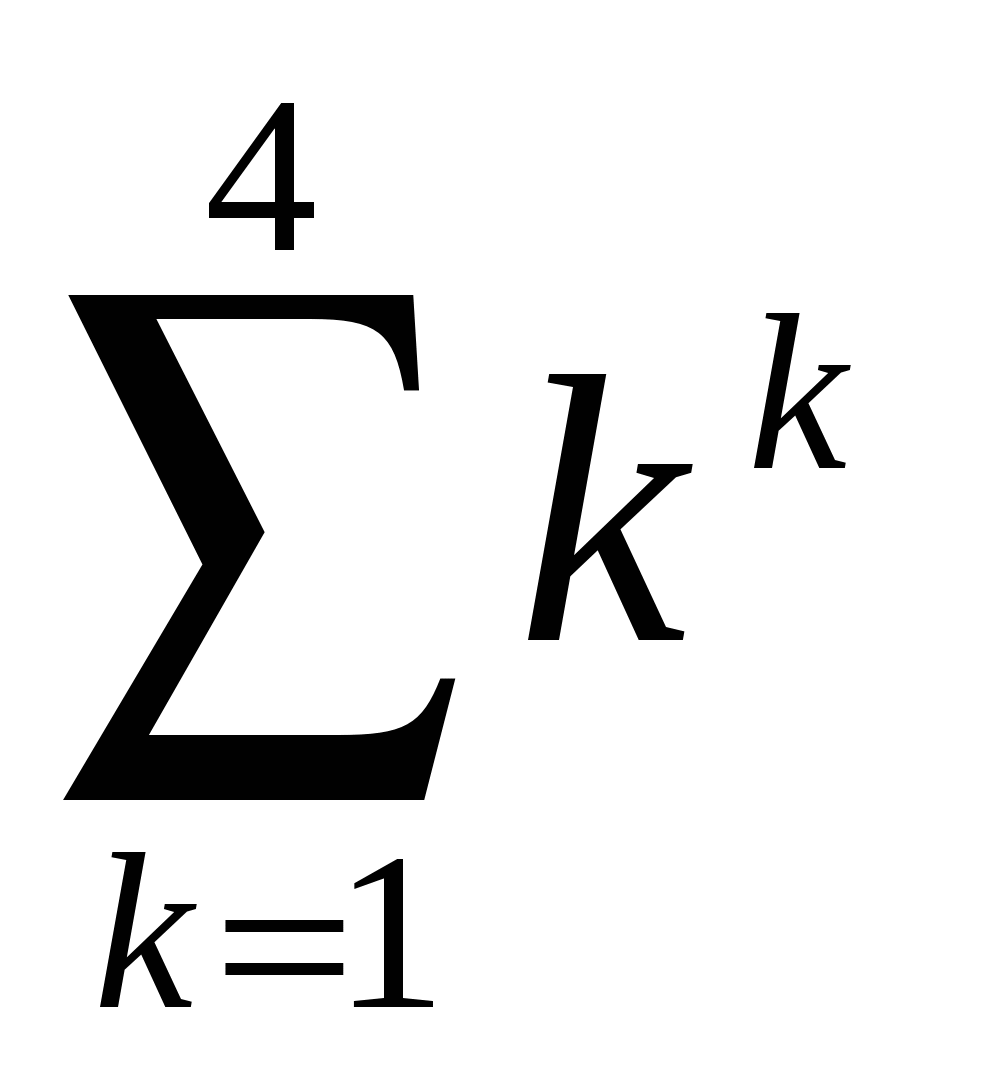 . .
Обчислити 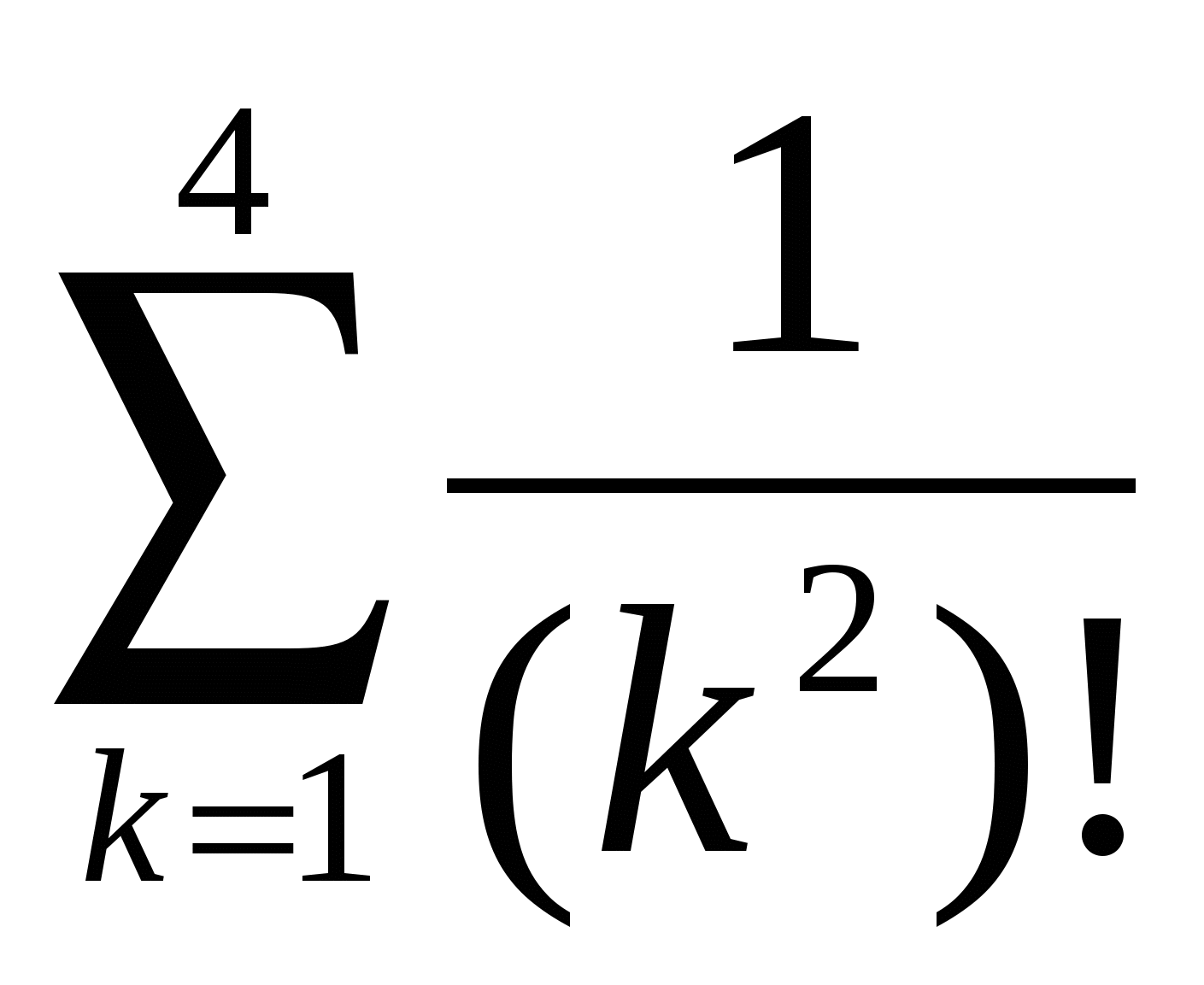 . .
Обчислити 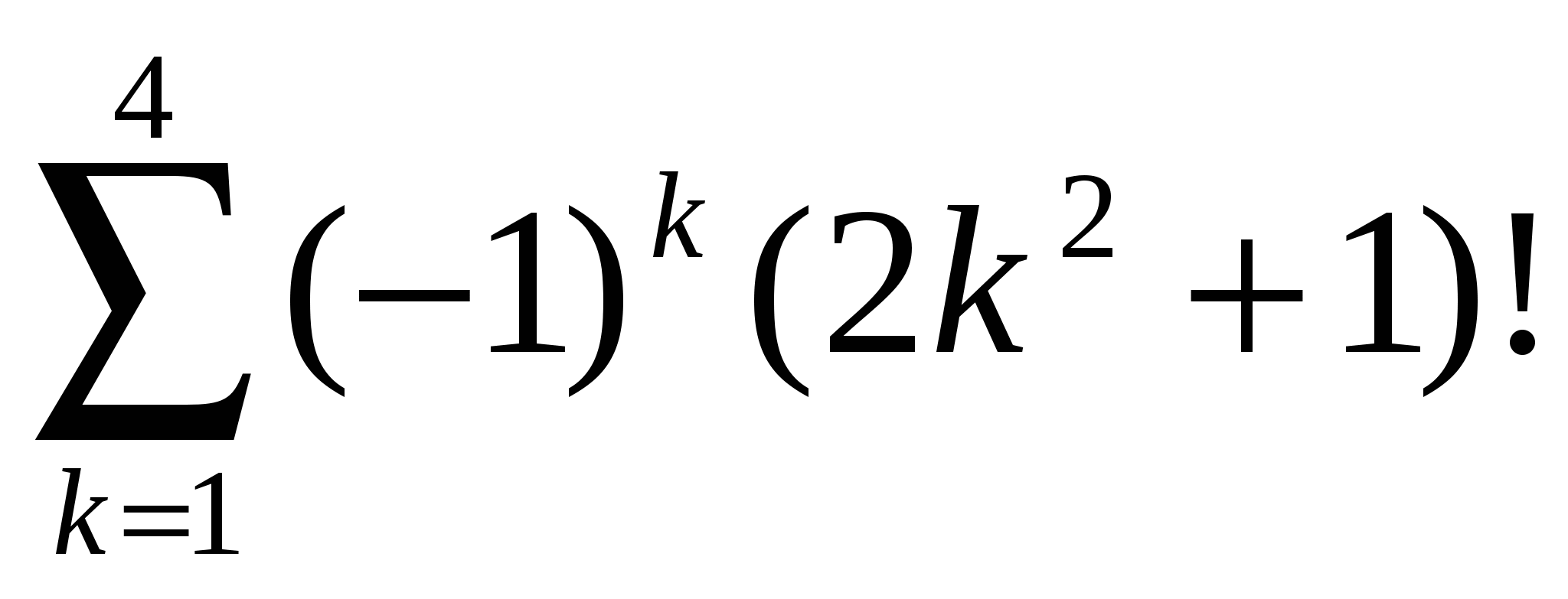 . .
Обчислити 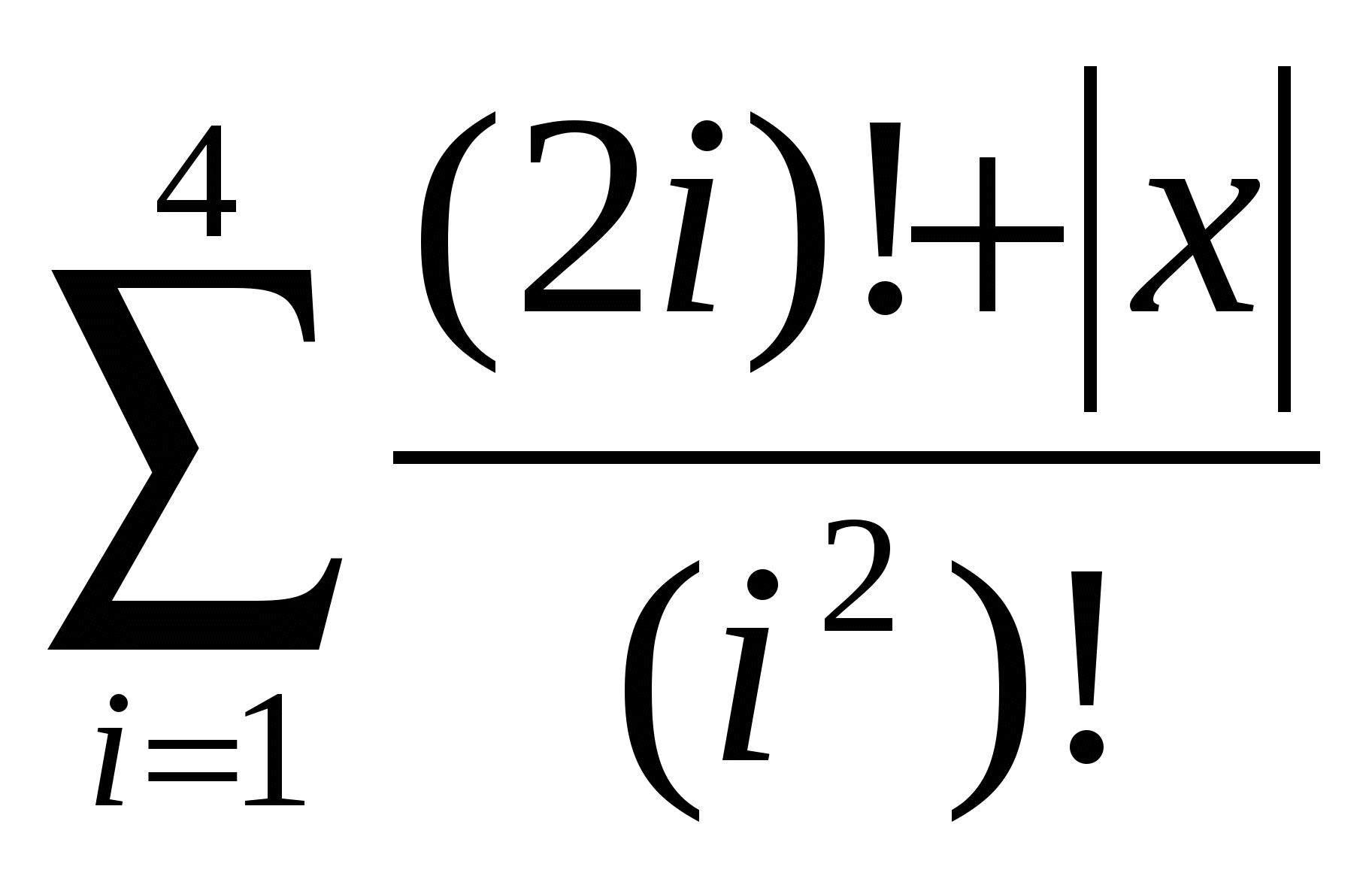 . .
Обчислити 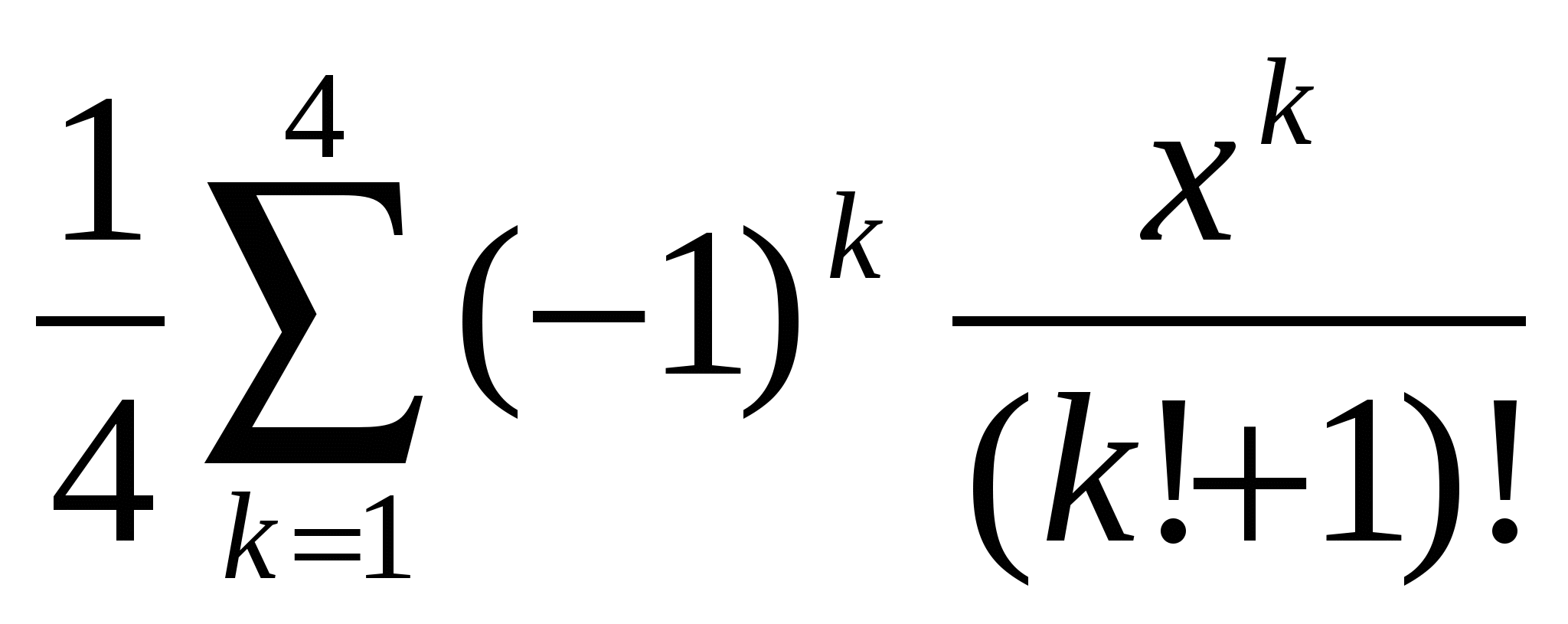 . .
Обчислити 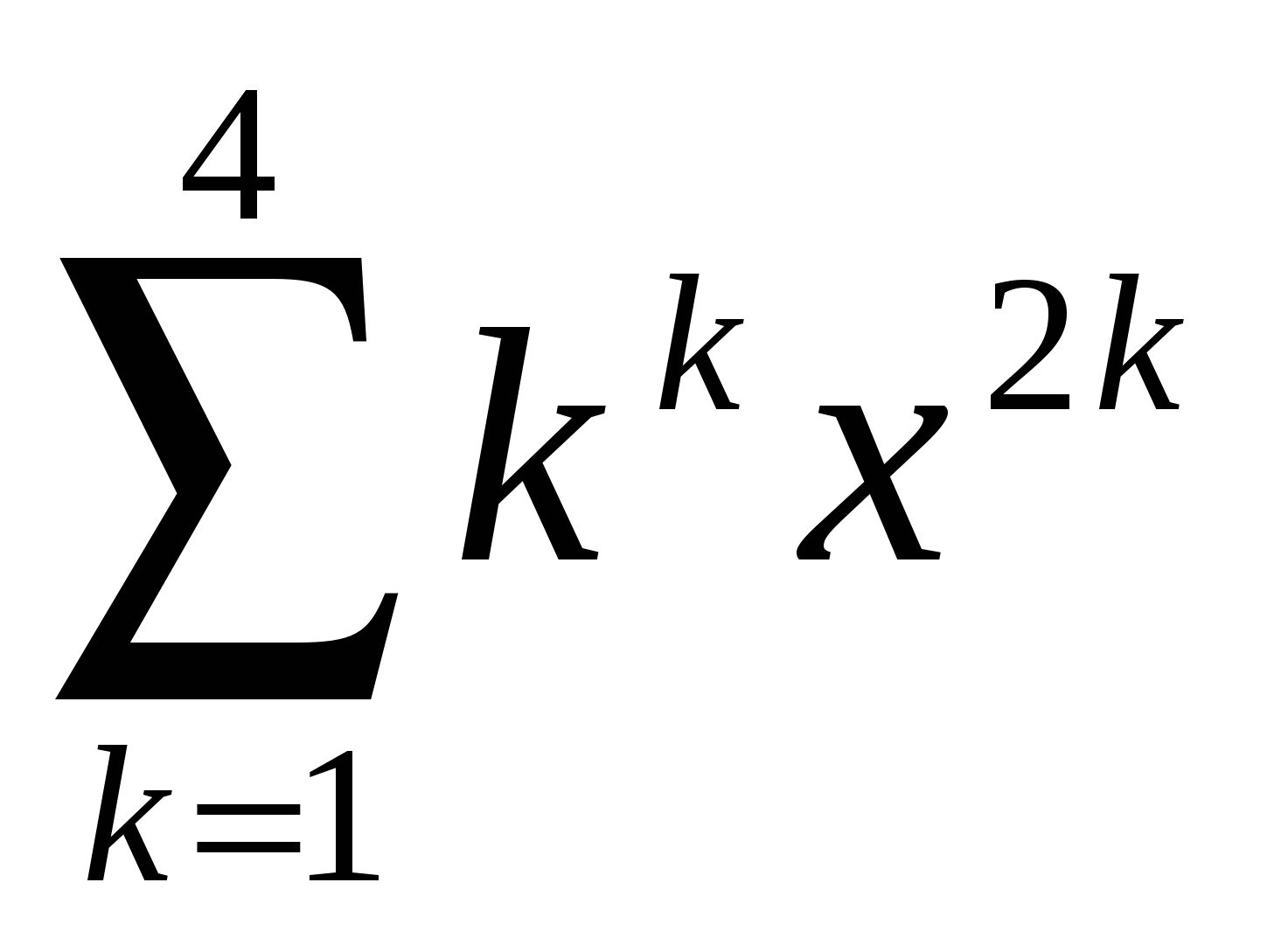 . .
Обчислити 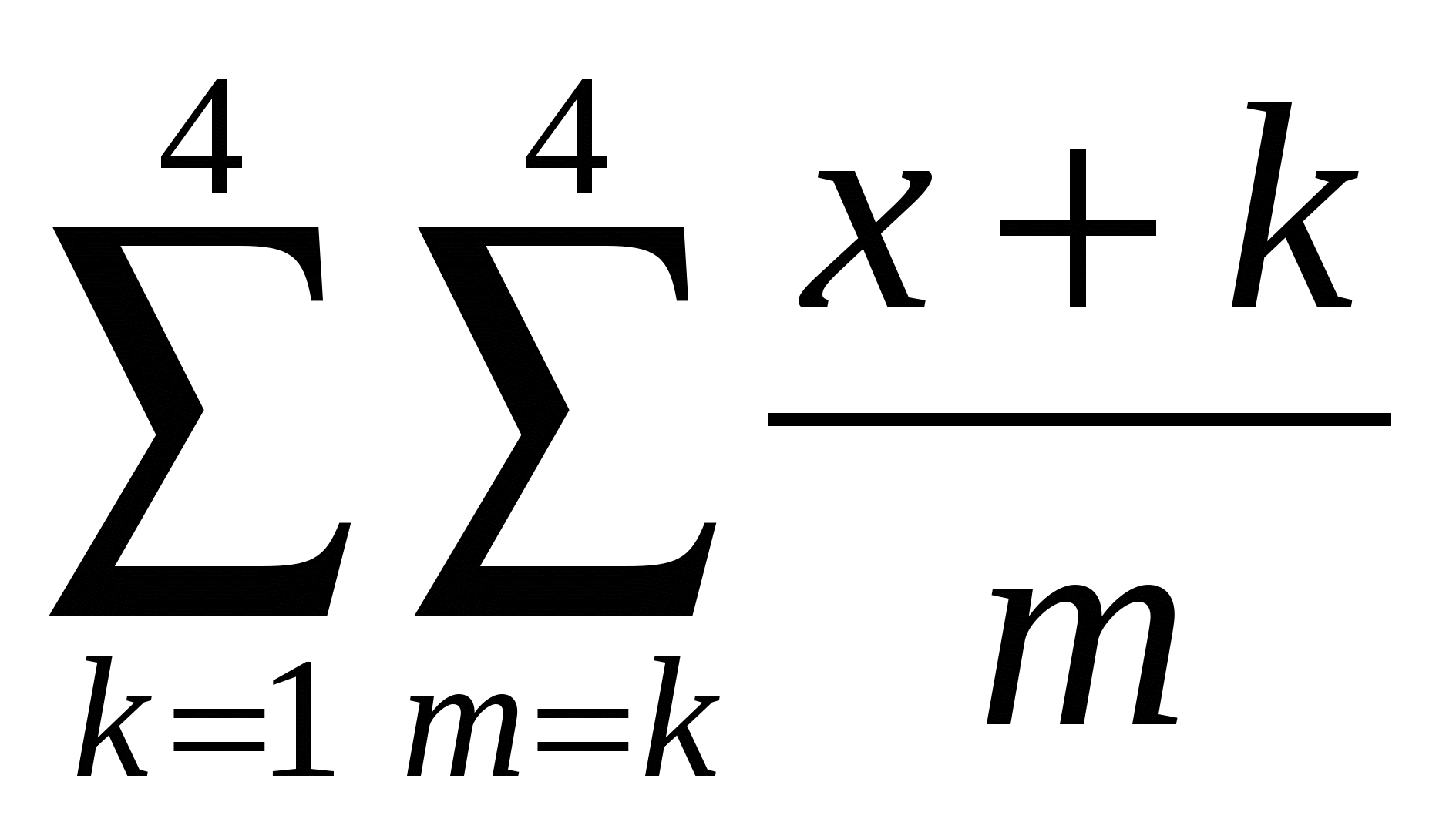 . .
Дані дійсні числа a1,a2,a3,a4. Обчислити a1+a22+…+a44
Дано натуральне число n. Одержати добуток f0 f1…fn,
де 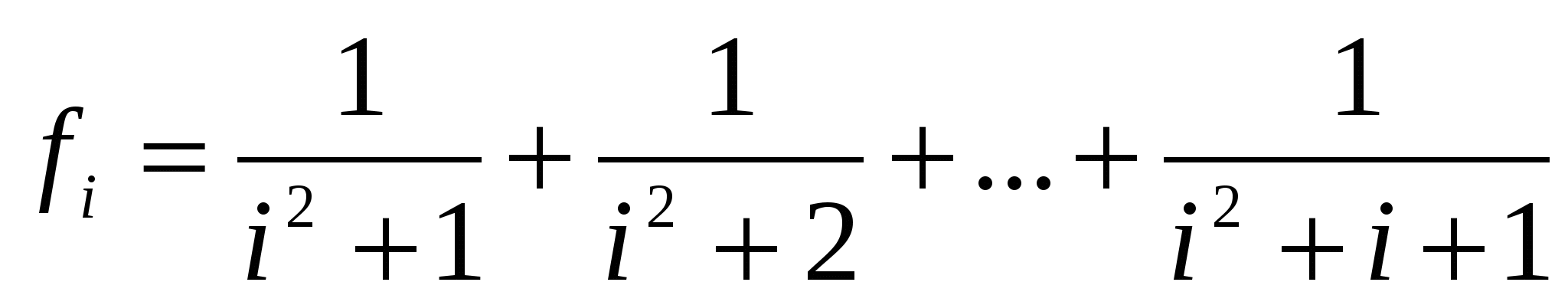 . .
Дано дійсні числа a1,a2,a3,a4. Одержати послідовність b1,b2,b3,…,b10,
де b1= a1+a2+a3+a4, b2= a12+a22+a32+a42, b3= a13+a23+a33+a43 ,…
Обчислити 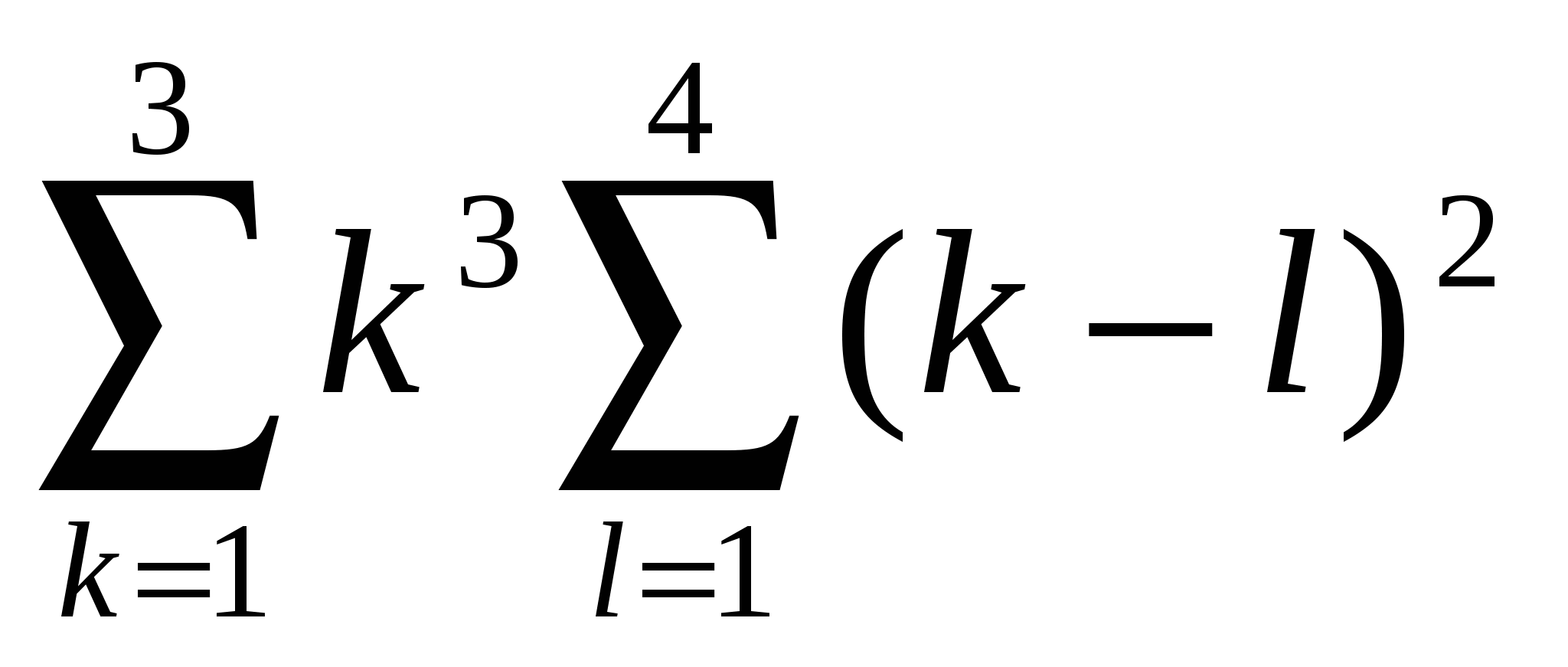 . .
Дані натуральні числа m і n, дійсні числа a1,a2,a3,…,anm. Обчислити
a1a2…am+am+1am+2…a2m+…
Дано натуральне число n. Одержати всі натуральні числа, менші n і взаємно прості з ними.
Дані цілі числа p і q. Одержати всі дільники числа q, що взаємно прості з p.
Дано натуральне число n. Одержати всі прості дільники цього числа.
Знайти найменше натуральне число n, що подане двома різними способами у виді суми кубів двох натуральних чисел x3+y3, (x y).
Дані натуральні числа a, b,(a b). Одержати всі прості числа p, що задовольняють нерівностям a ≤ p ≤ b.
Знайти перші 100 простих чисел.
Дані натуральні числа m і n. Одержати всі менші n натуральні числа, квадрат суми цифр яких дорівнює m.
Дано натуральне число n. Зазначити всі трійки натуральних чисел x,y,z, для яких n=x2+y2+z2.
Обчислити 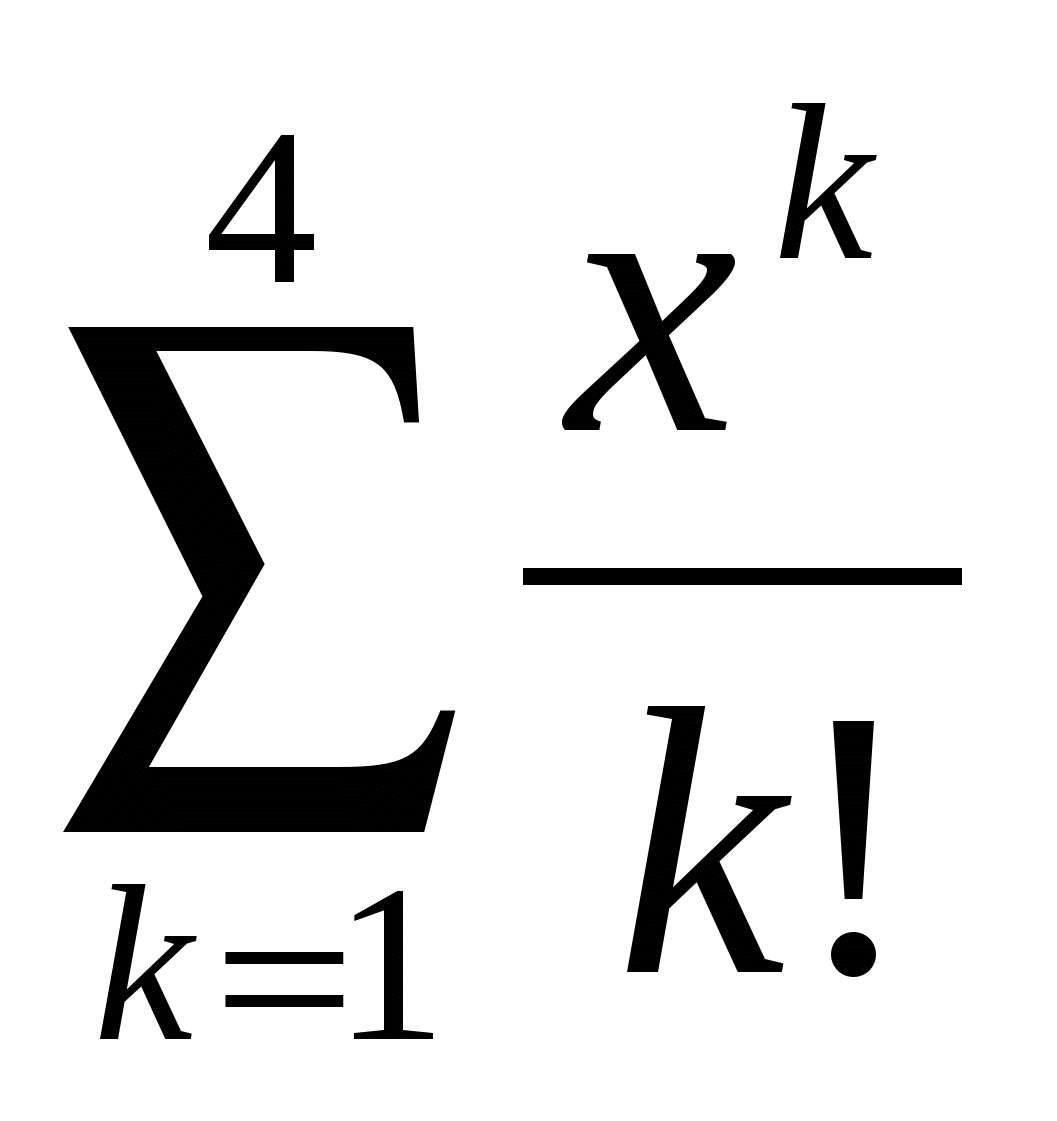 . .
Обчислити 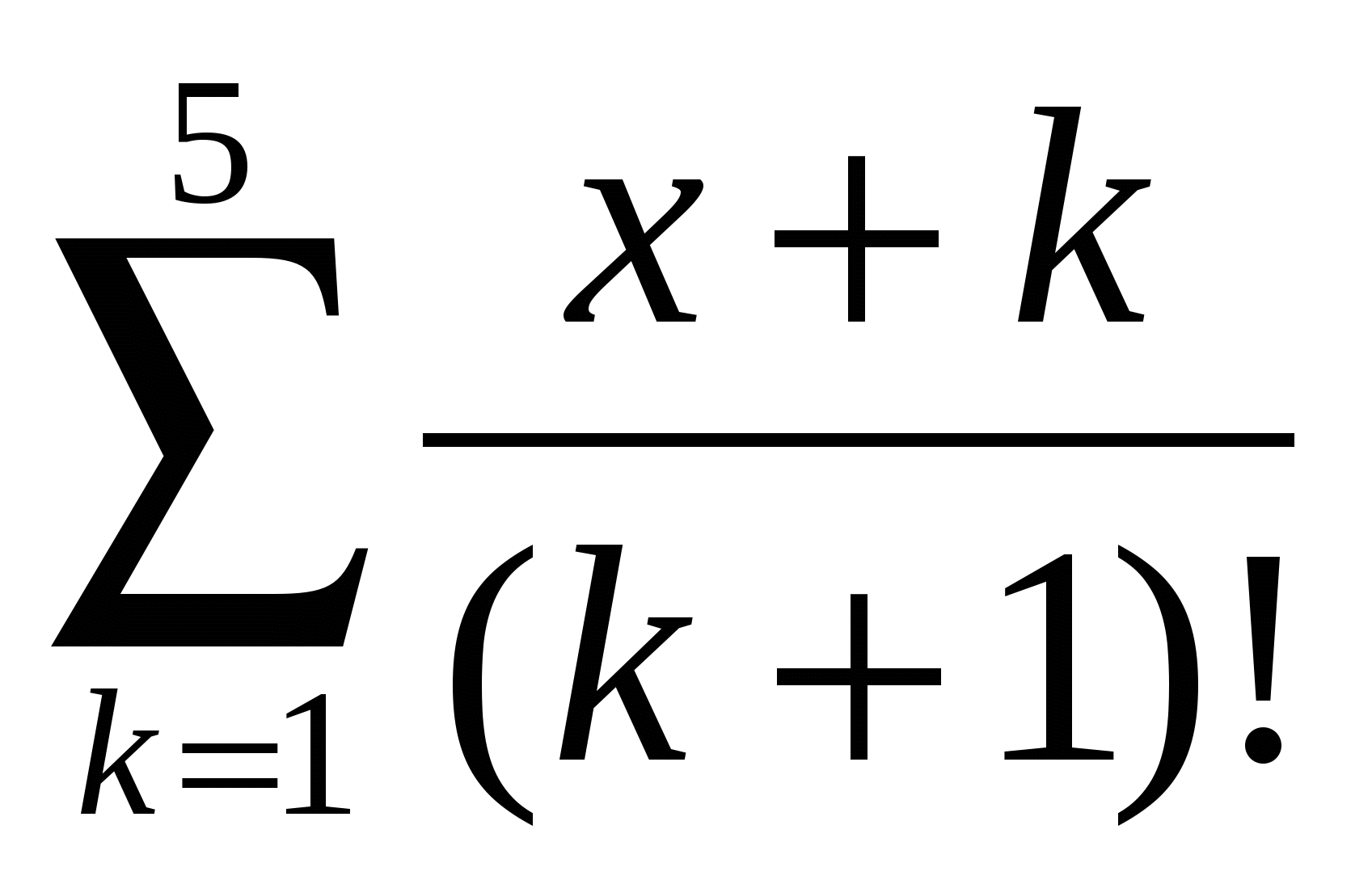 . .
Обчислити 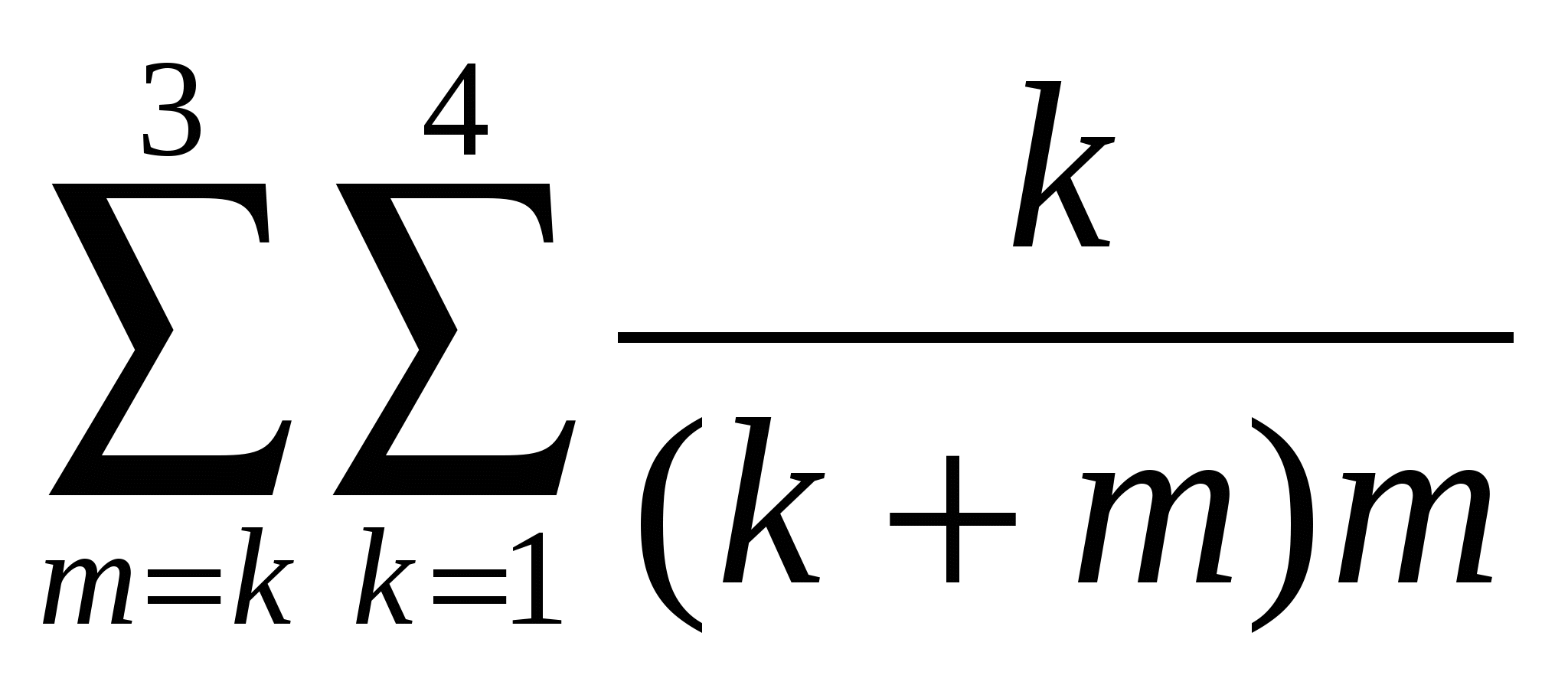 . .
Обчислити 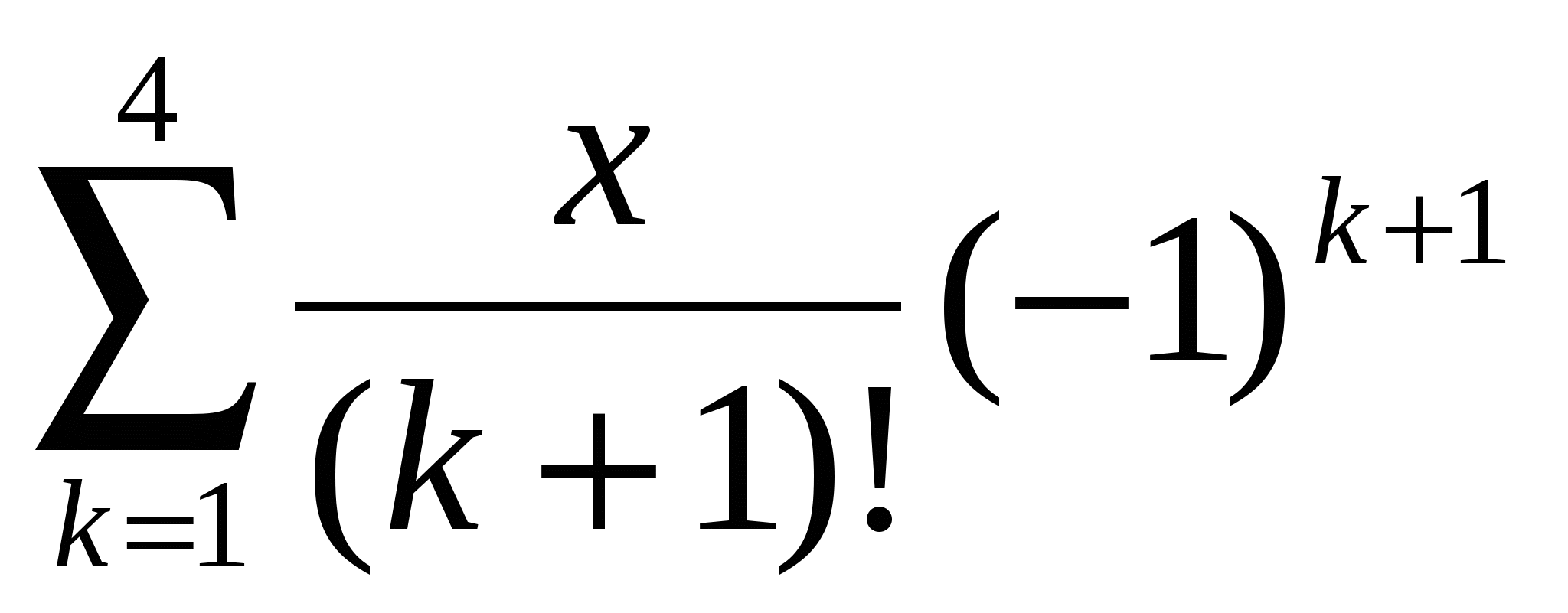 . .
Дані дійсні числа a1,a2,…a10, b1,b2,…b20. Одержати дійсну матрицю С, у якої 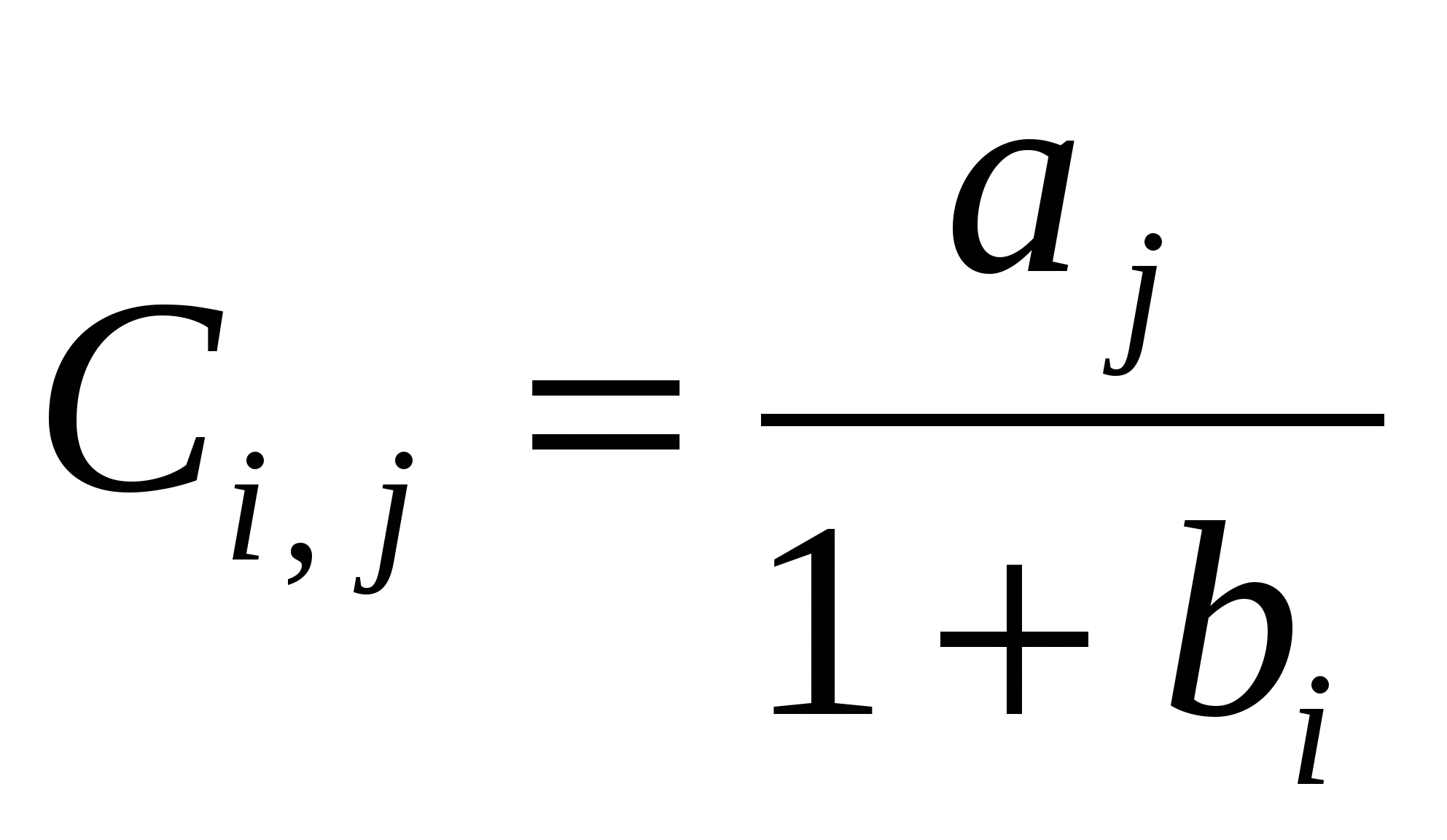 , i =1,2,…,10; j=1,2,…,20. , i =1,2,…,10; j=1,2,…,20.
Контрольні запитання
Що таке цикл? Які переваги використання циклів в алгоритмах?
Як організувати цикл?
Які оператори використовуються при класичній організації циклів?
Як організувати цикл з наперед невідомою кількістю повторень?
Що таке „ітераційний” цикл?
Як записується оператор циклу з параметром FOR?
Як організувати цикл із дробовим кроком?
Як організувати „вкладені” цикли?
Як представити схему алгоритму обчислення суми?
Який вигляд має схема алгоритму обчислення добутку?
Який вигляд має алгоритм пошуку найбільшого елемента масиву?
Який вигляд має схема алгоритму пошуку найменшого елемента масиву?
ЛАБОРАТОРНА РОБОТА 7
ВВЕДЕННЯ І ВИВЕДЕННЯ МАСИВІВ ІНФОРМАЦІЇ
Мета роботи: отримання практичних навиків розробки алгоритмів і програм, що здійснюють введення і виведення різноманітних інформаційних масивів.
Робоче завдання
Скласти схему алгоритму і розробити програму, що виконують такі дії:
виведення заголовка лабораторної роботи, у якому вказується найменування лабораторної роботи, її номер, варіант індивідуального завдання, прізвище студента та навчальна група;
введення одномірного масиву (вектору);
виведення значень одномірного масиву разом із їх іменами;
виведення значень одномірного масиву з p-го по q-й елемент;
введення двомірного масиву (матриці);
виведення рядка матриці з номером r;
виведення стовпчика матриці з номером s;
виведення всіх елементів масиву у вигляді матриці з заданим інтервалом k між елементами.
Варіанти індивідуальних завдань для виконання першої частити лабораторної роботи
Таблиця 2
Номер варіан-та
|
Одномірний масив
|
Двомірний масив
|
Ім'я масиву
|
Розмір масиву
|
p
|
q
|
Формат виведення
|
Ім'я масиву
|
Розмір масиву
|
r
|
s
|
k
|
Формат виведення
|
1
|
ZOR
|
4
|
2
|
4
|
6:2
|
Z2
|
4×4
|
3
|
2
|
2
|
6:1
|
2
|
PIK
|
5
|
1
|
3
|
4:2
| RZK |
4×3
|
4
|
1
|
3
|
5:0
|
3
|
D17
|
4
|
2
|
3
|
5:1
|
AII
|
5×3
|
4
|
2
|
2
|
5:3
|
4
|
RA
|
5
|
4
|
5
|
4:1
|
CKA
|
3×5
|
3
|
4
|
2
|
4:1
|
5
|
AL1
|
4
|
2
|
3
|
5:2
|
VIK
|
3×3
|
2
|
3
|
3
|
10:3
|
6
|
DAN
|
5
|
2
|
5
|
4:1
|
S10
|
3×4
|
3
|
2
|
2
|
5:2
|
7
|
KAN
|
7
|
4
|
5
|
3:1
|
RD5
|
2×5
|
2
|
4
|
1
|
6:3
|
8
|
A2K
|
5
|
3
|
5
|
3:1
|
SIR
|
3×5
|
1
|
4
|
1
|
4:1
|
9
|
WR
|
4
|
2
|
4
|
4:2
|
UNI
|
5×2
|
4
|
2
|
2
|
9:2
|
10
|
VAN
|
8
|
4
|
7
|
3:1
|
K57
|
3×3
|
3
|
2
|
2
|
8:1
|
11
|
SLI
|
9
|
4
|
8
|
3:1
|
CH1
|
3×5
|
2
|
4
|
2
|
4:2
|
12
|
ALF
|
8
|
4
|
8
|
5:3
|
GTRN
|
4×5
|
4
|
4
|
2
|
6:2
|
13
|
HELI
|
5
|
3
|
5
|
5:3
|
SKAZ
|
4×4
|
3
|
2
|
3
|
5:3
|
14
|
PRI1
|
6
|
3
|
4
|
6:3
|
RAB
|
3×4
|
3
|
3
|
2
|
6:1
| |
 Скачать 1.84 Mb.
Скачать 1.84 Mb.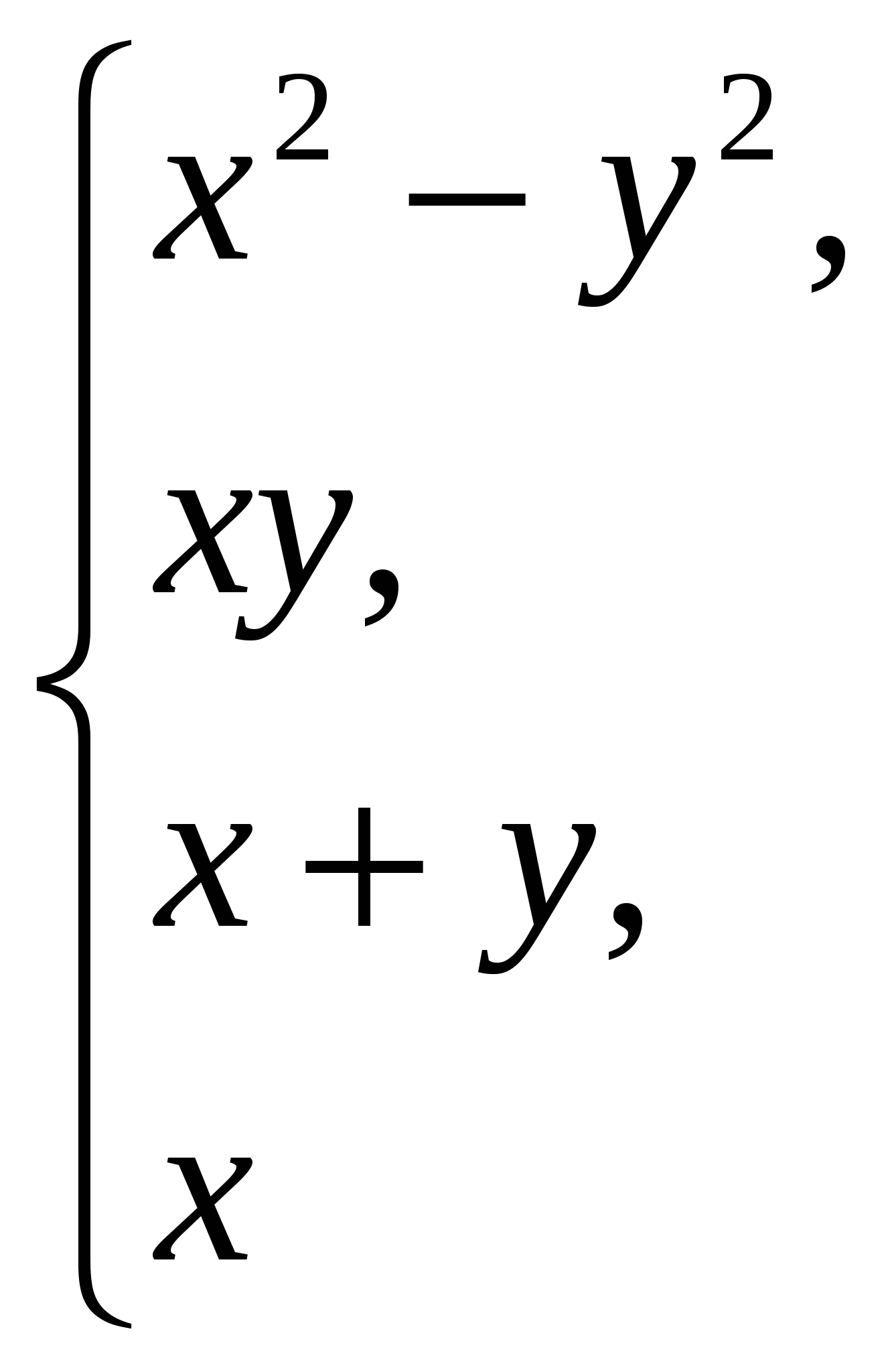
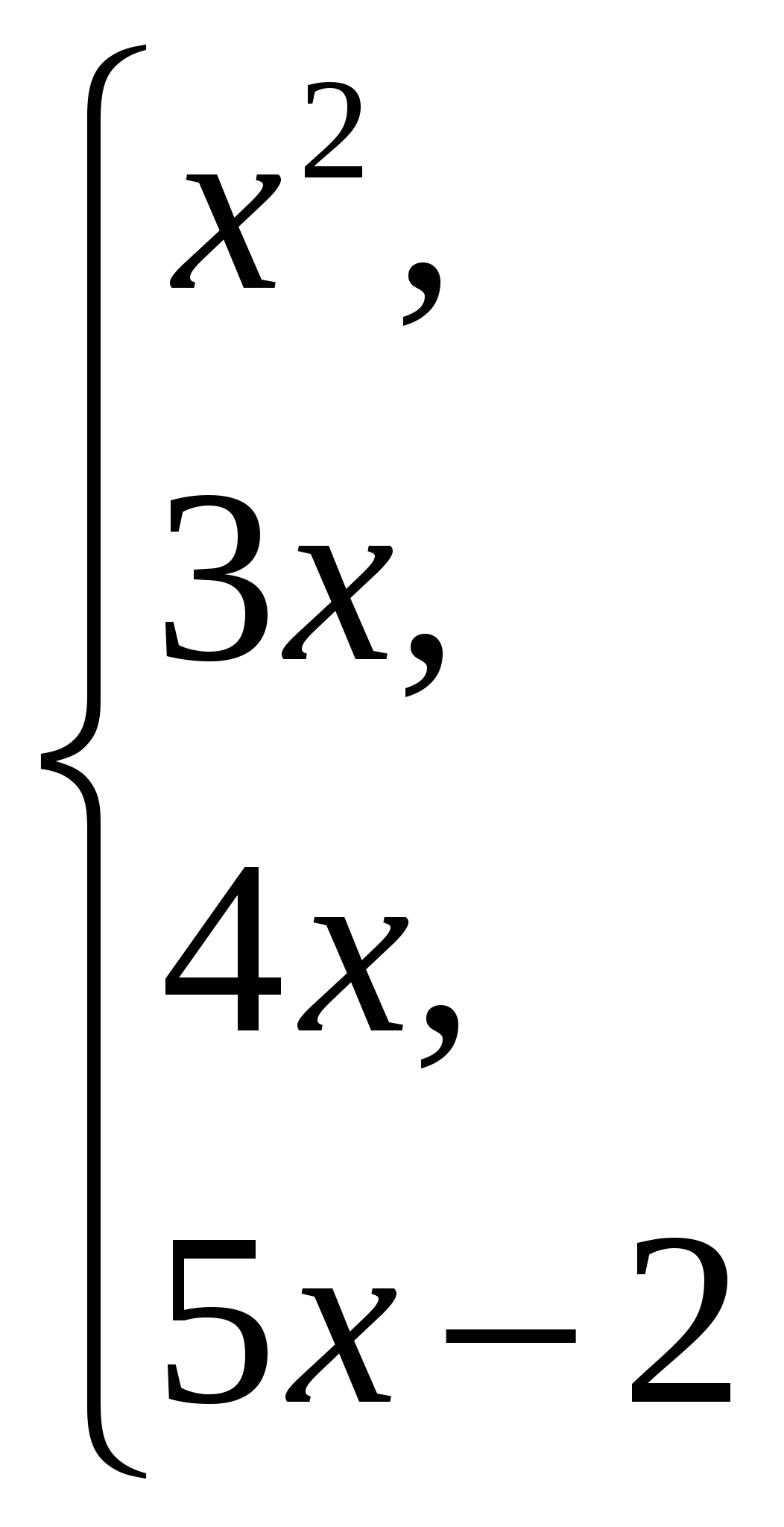
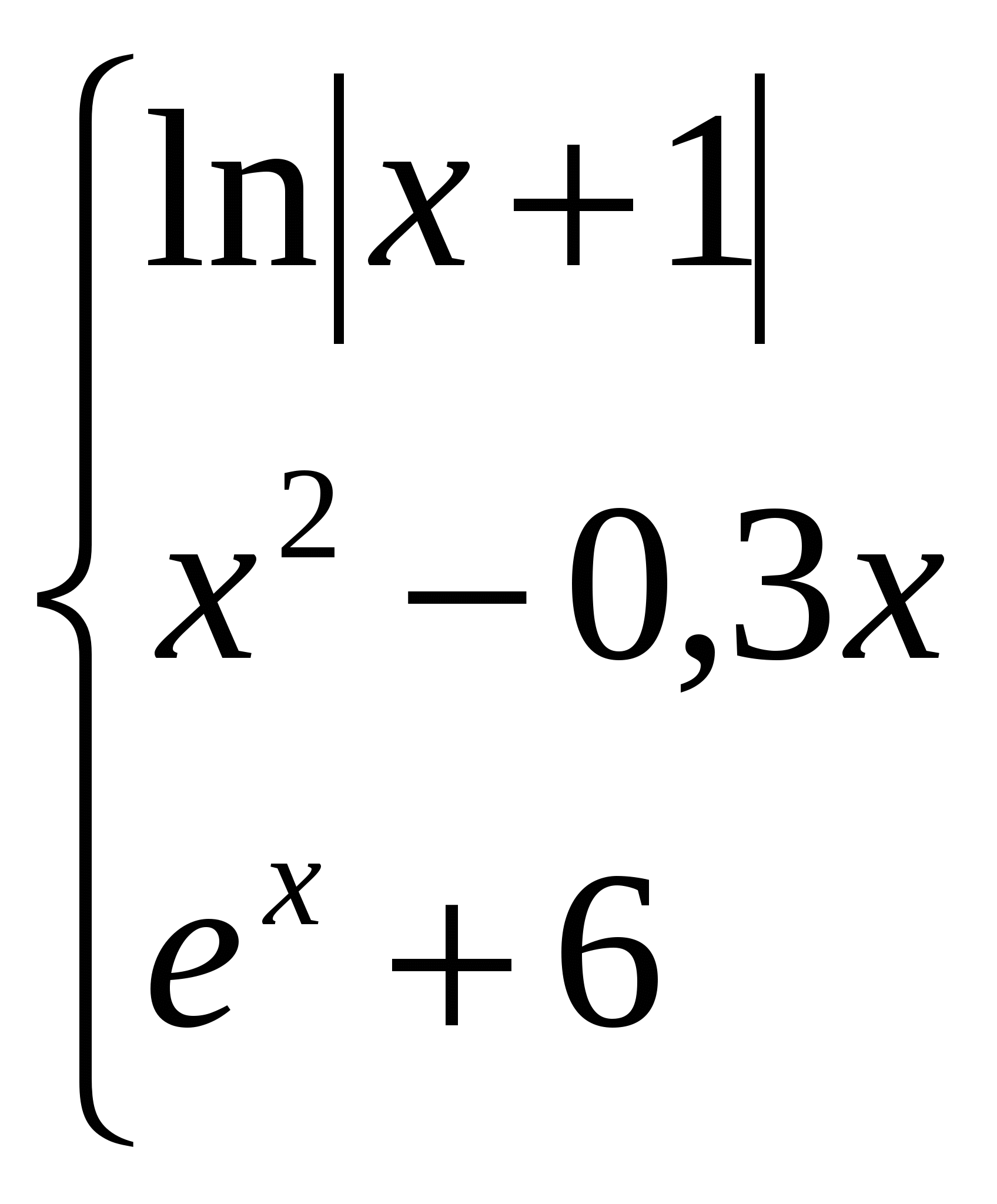
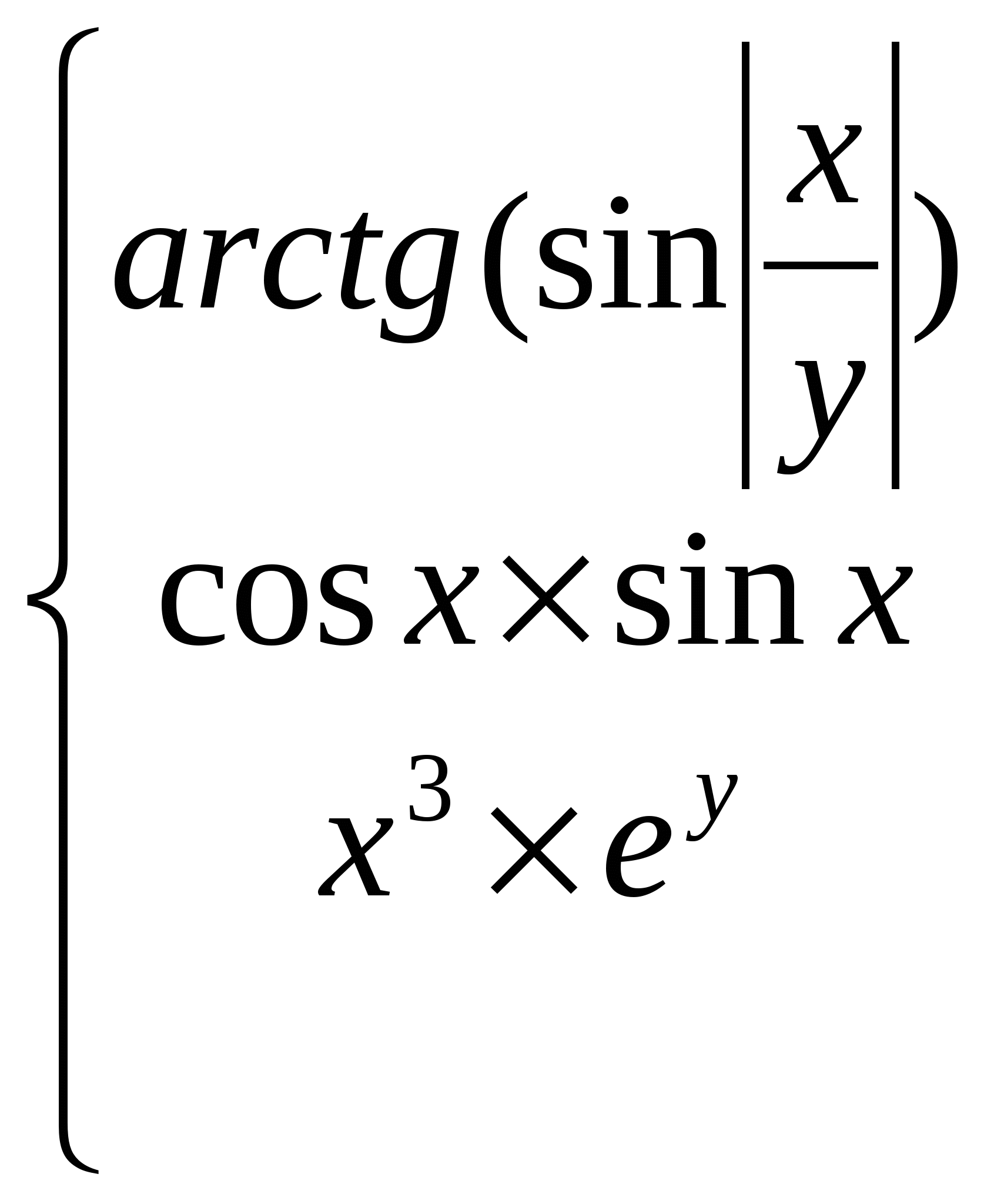
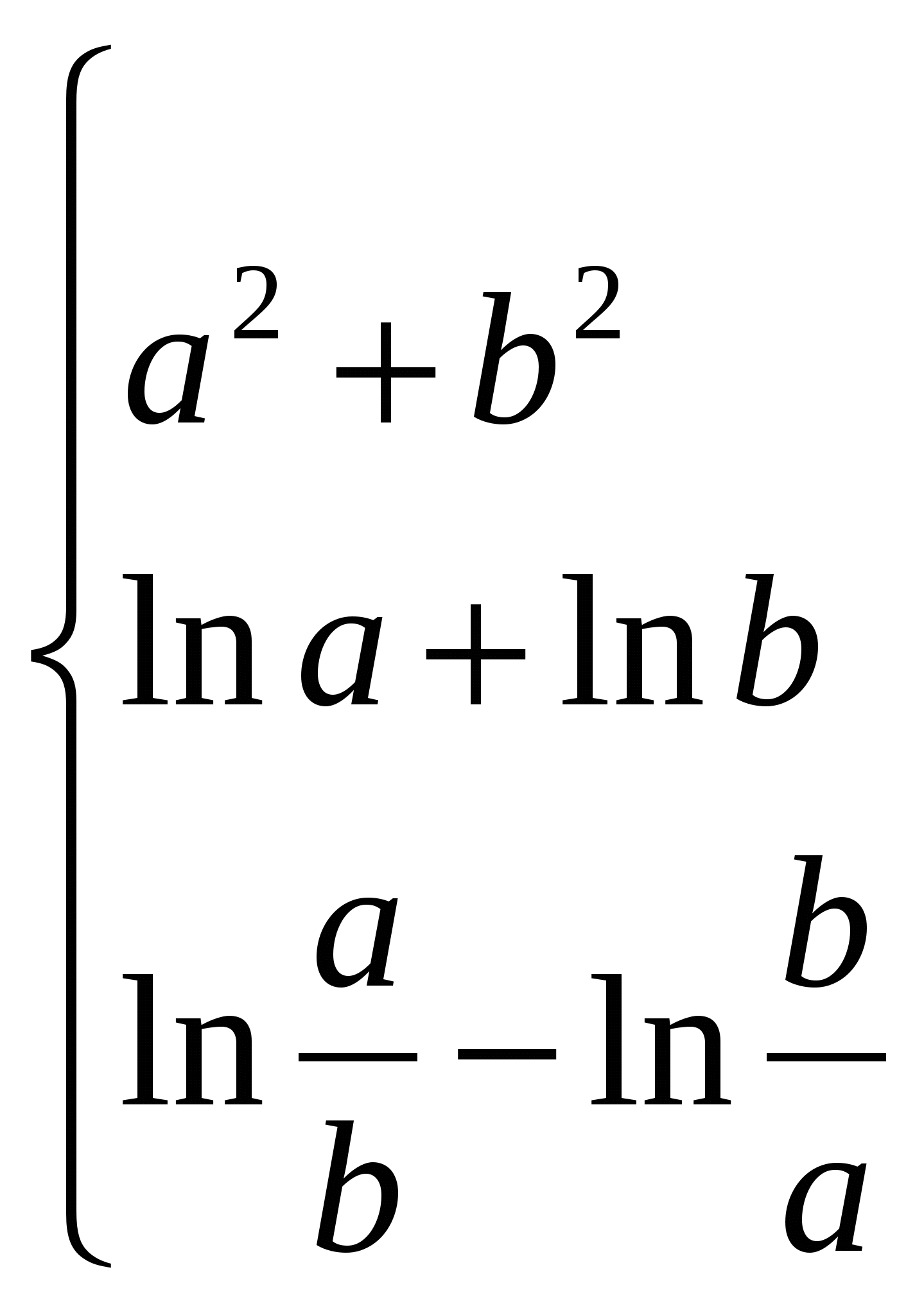
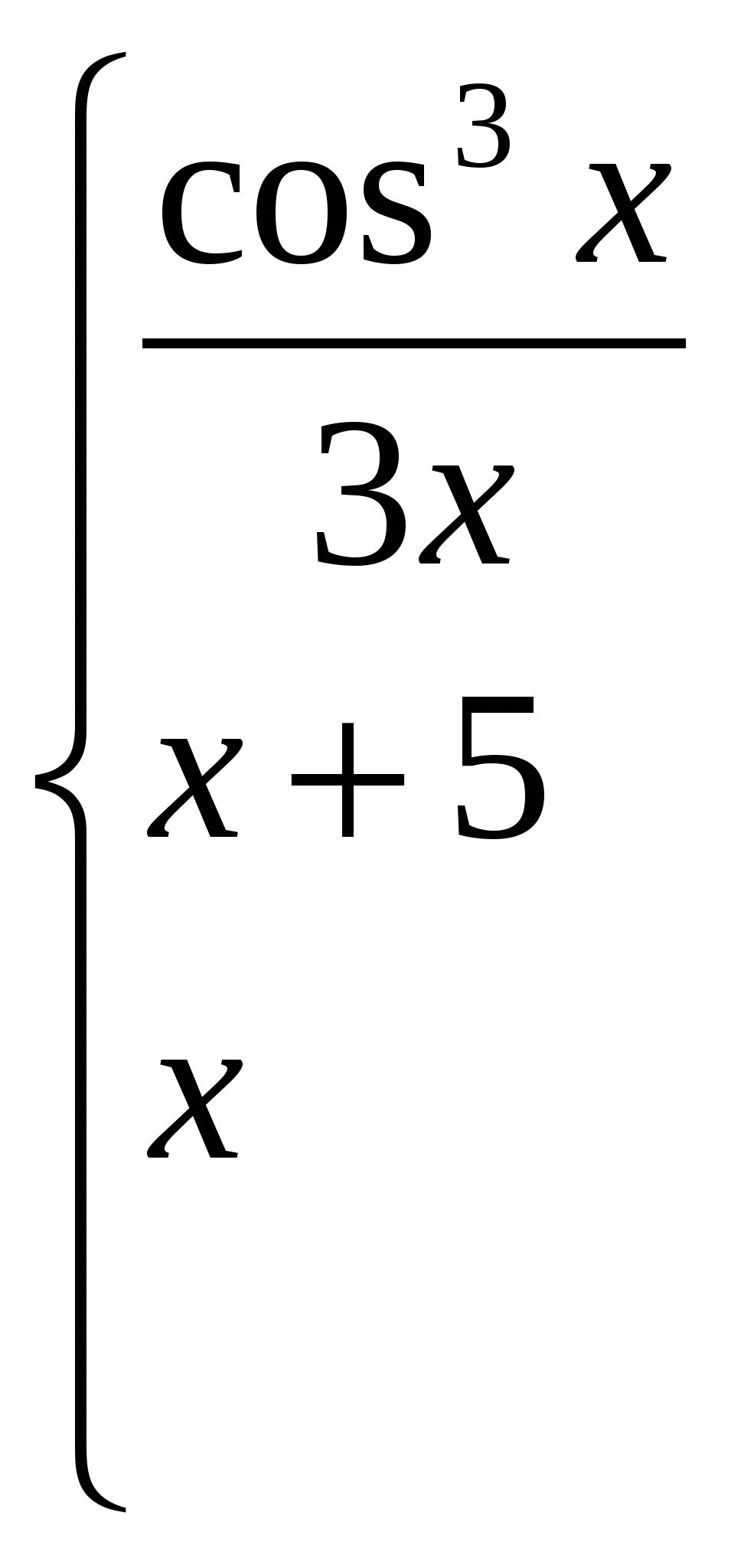
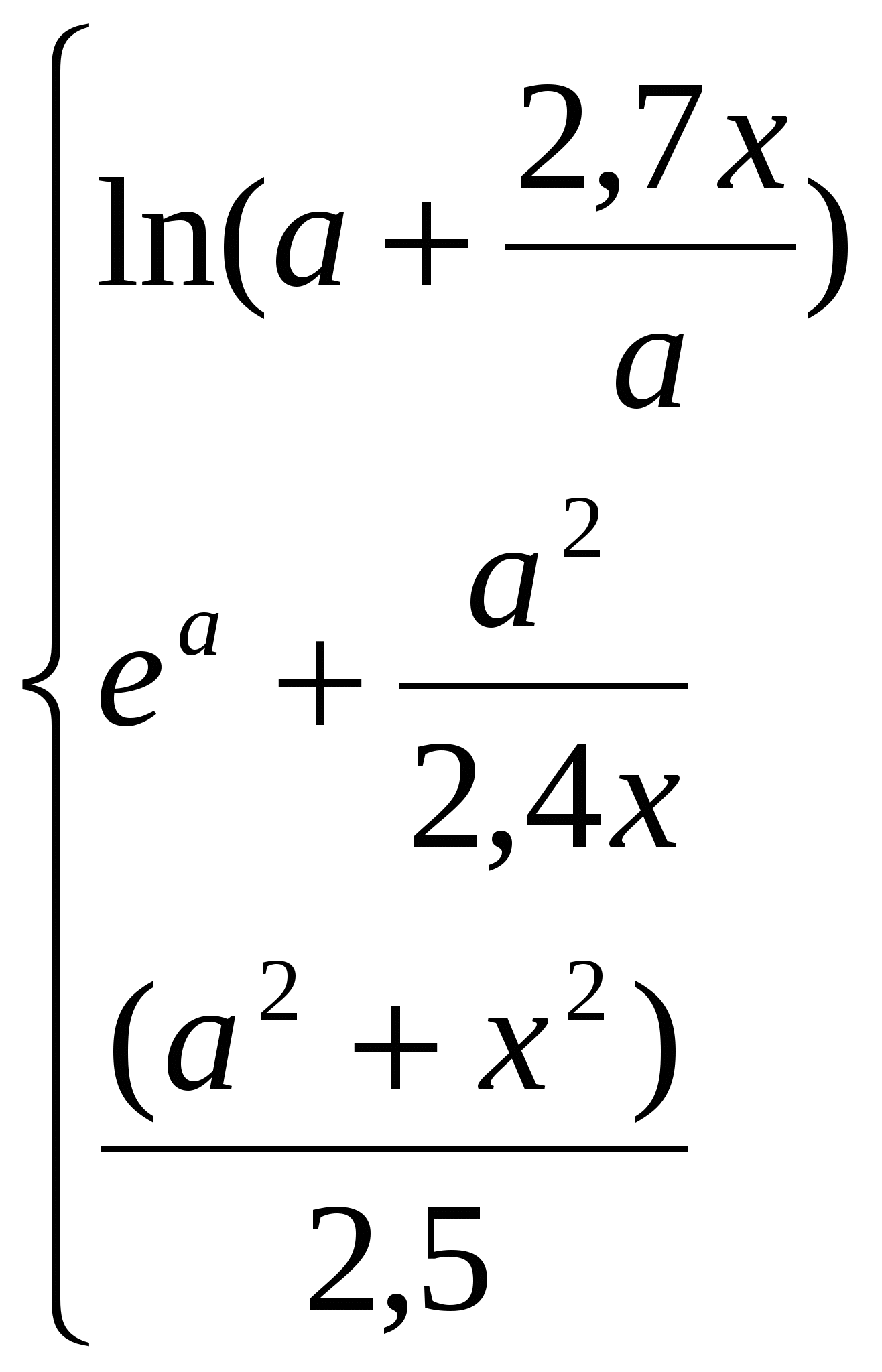
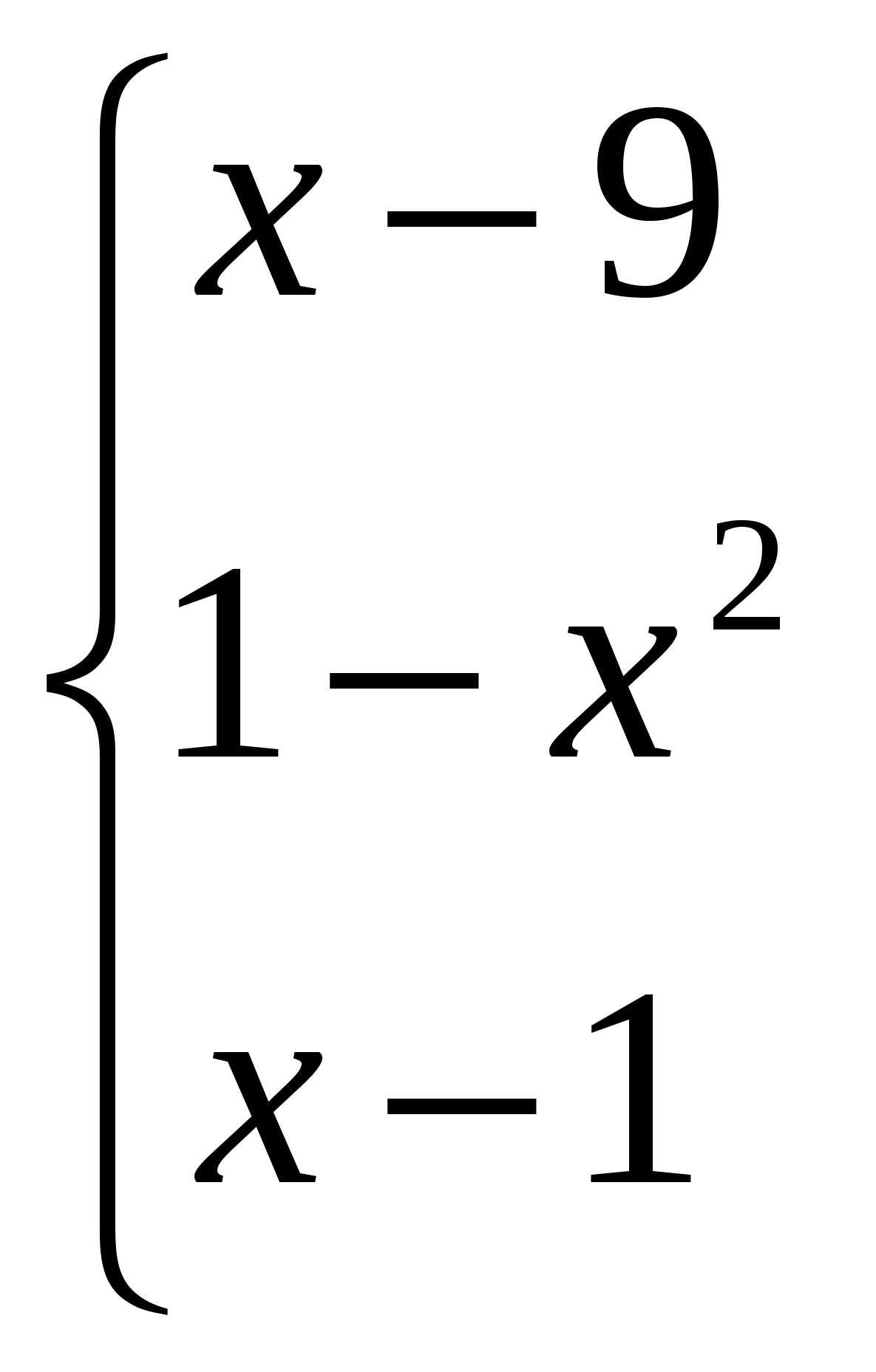

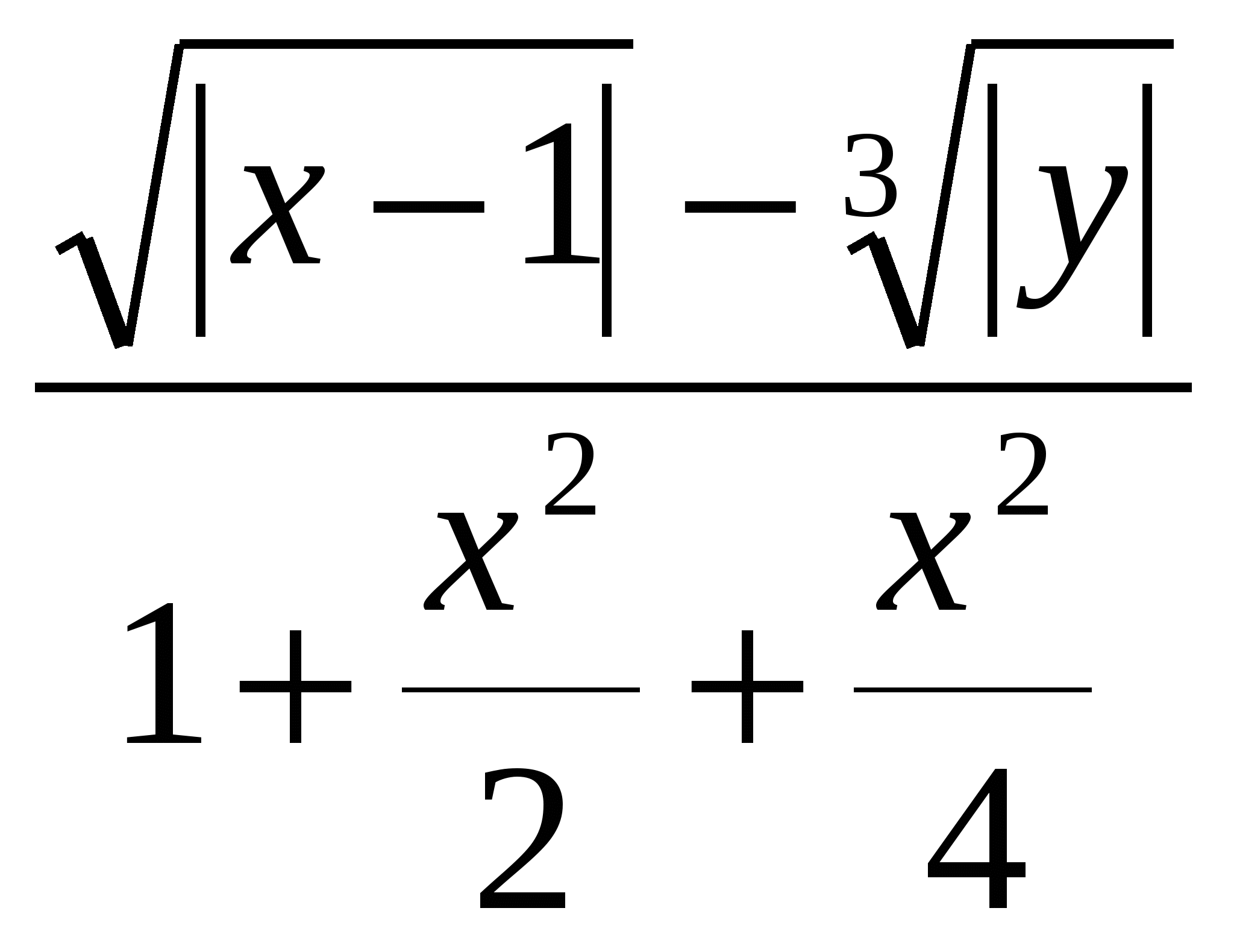 ;
; 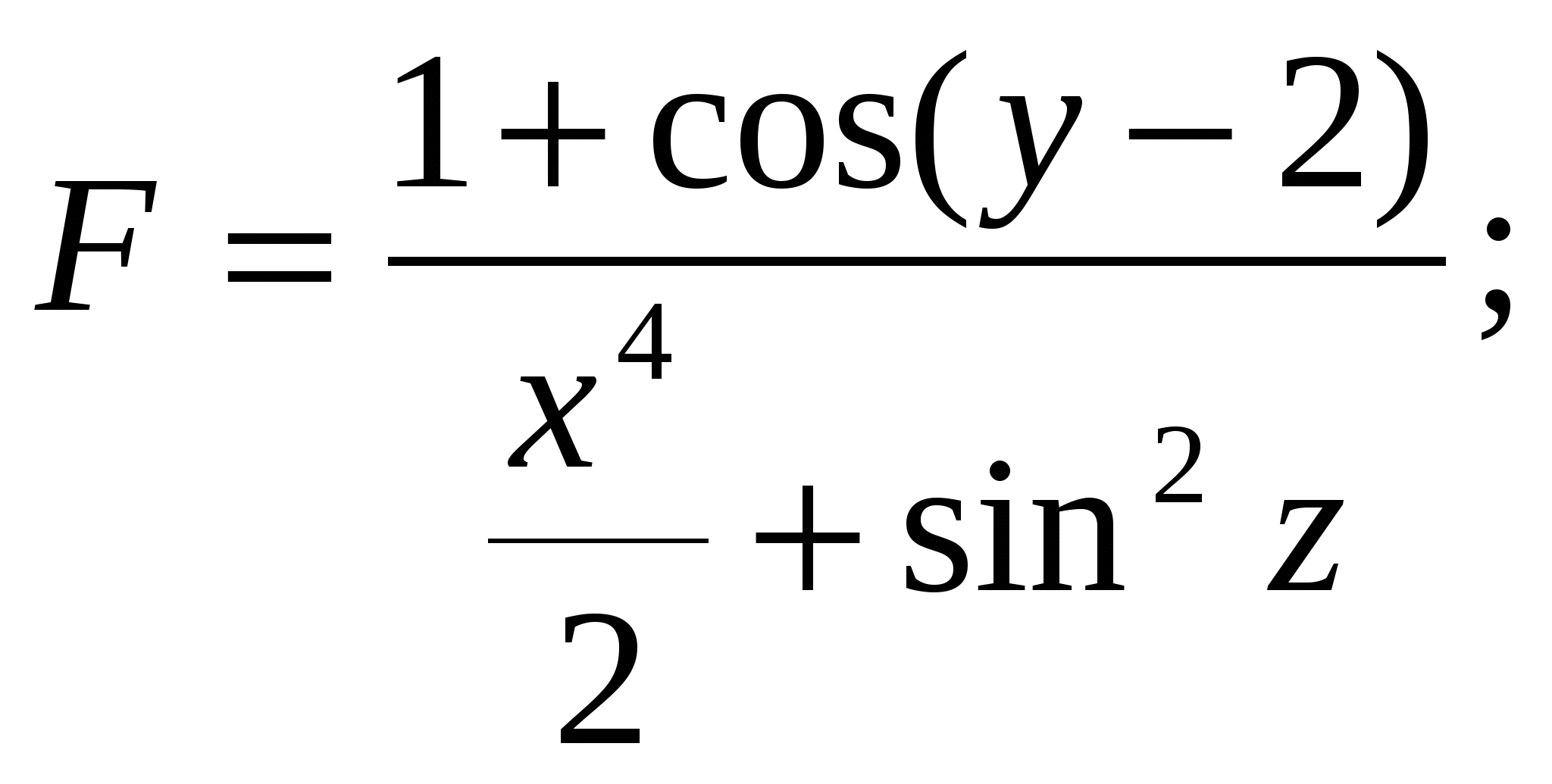
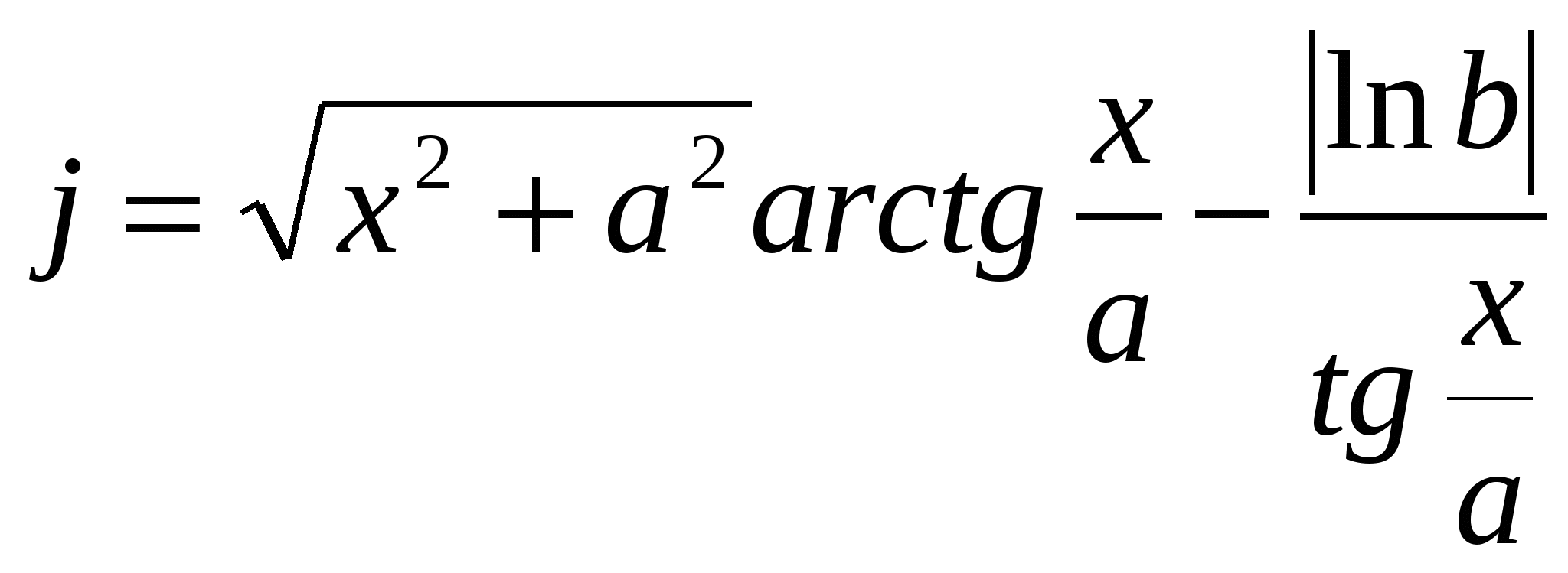 ; z=(sin2a+cos 2b ln x - tg y) d,
; z=(sin2a+cos 2b ln x - tg y) d, 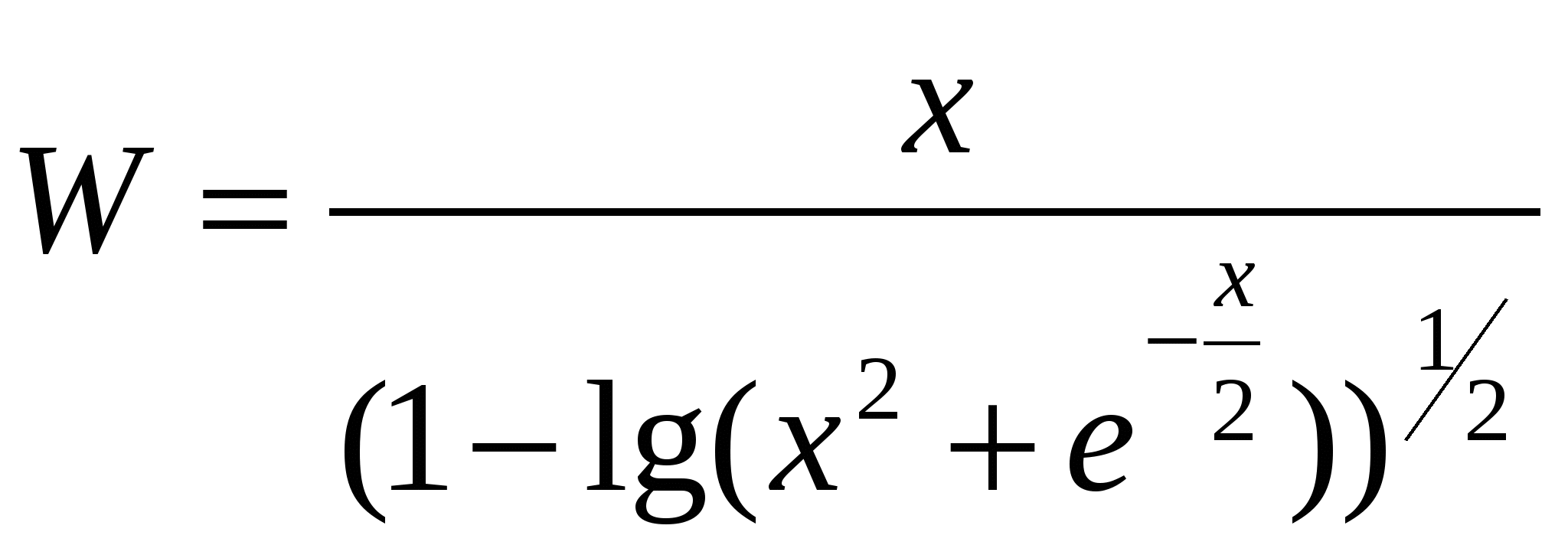 ;
; 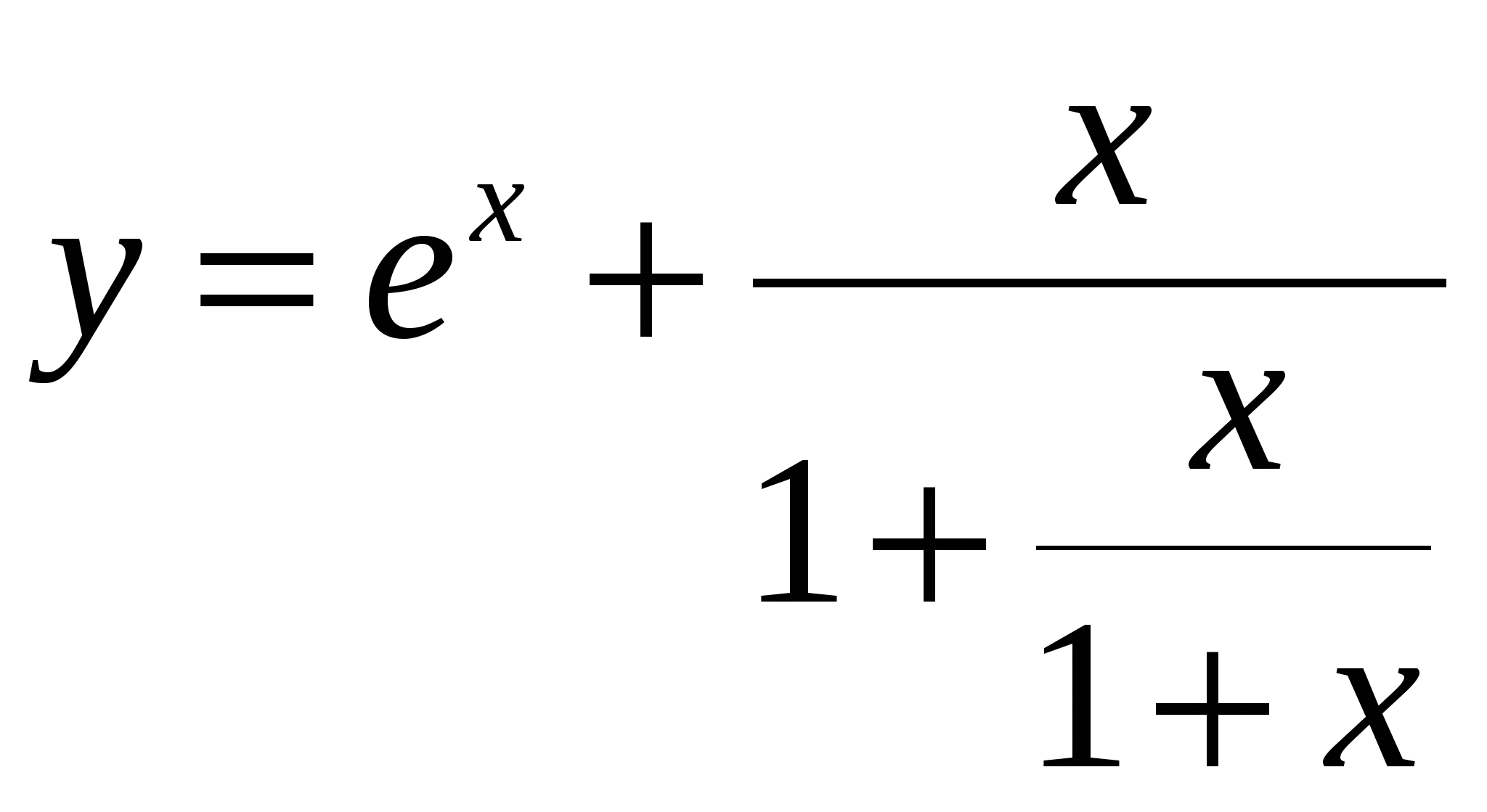 ; d= ((a+b+c)/2
; d= ((a+b+c)/2