ЛАБОРАТОРНА РОБОТА 9
МАТРИЧНІ ПЕРЕТВОРЕННЯ
Мета роботи: отримання практичних навичків розробки алгоритмів комбінованої (розгалуженої та циклічної) структури й створення програм на прикладі перетворення матриць.
Робоче завдання
Скласти алгоритм та розробити програму, які виконують наступні дії:
виведення заголовка лабораторної роботи, у якому вказується найменування лабораторної роботи, її номер, варіант індивідуального завдання, прізвище студента та навчальна група;
введення початкових даних та виконання дій згідно варіанта індивідуального завдання;
виведення початкових даних та результатів виконання лабораторної роботи.
Варіанти індивідуальних завдань для виконання лабораторної роботи
Дано квадратну матрицю. Поміняти місцями елементи головної і побічної діагоналей, попередньо впорядкувавши першу за зростанням елементів.
У квадратній матриці переставити рядки таким чином, щоб кількість ненульових елементів у рядках зростали від першого рядка до останнього.
Нормувати квадратну матрицю, розділивши всі елементи кожного рядка на максимальний за модулем елемент цього рядка.
У прямокутній матриці переставити стовпчики таким чином, щоб сума елементів стовпчика зростала від першого стовпчика до останнього.
Дано двомірний масив А. Одержати новий масив В, у якому всі елементи масиву А розділені на найближчий до р елемент масиву, попередньо розташувавши всі елементи останнього стовпчика вихідного масиву за спаданням.
У квадратній матриці D переставити місцями n-й і k-й стовпчики, попередньо розташувавши їх елементи за спаданням.
У квадратній матриці Р переставити місцями елементи побічної діагоналі і k-го стовпчика, попередньо впорядкувавши елементи діагоналі за спаданням.
Дано квадратну матрицю. Одержати нову матрицю шляхом заміни місцями елементів першого рядка й останнього стовпчика, попередньо впорядкувавши елементи стовпчика за спаданням.
У квадратній матриці D поміняти місцями елементи побічної діагоналі і l-го рядка, попередньо впорядкувавши елементи останього за зростанням.
З квадратної матриці А одержати матрицю В, у якій елементи першого стовпчика і першого рядка вихідної матриці упорядковані за зростанням.
Дано квадратну матрицю В. Одержати нову матрицю, у якій послідовною перестановкою рядків і стовпчиків найбільший елемент розташовувався б у правому нижньому куті, а найменший – в лівому верхньому.
Дано квадратну матрицю D, одержати нову матрицю Q, у якій елементи останнього рядка й останнього стовпчика вихідної матриці розташувалися за зростанням.
З вихідної квадратної матриці Q одержати нову матрицю Р шляхом заміни елементів головної і побічної діагоналей, попередньо впорядкувавши елементи головної діагоналі за зростанням їх модулей.
Дано квадратну матрицю R. Одержати нову матрицю, у якій елементи k-го рядка розділені на найбільший елемент r-го стовпчика, попередньо впорядкувавши за зростанням елементи k-го рядка.
З матриці К одержати нову матрицю D шляхом розташування рядків таким чином, щоб сума їх елементів убувала від першого рядка до останнього.
У квадратній матриці впорядкувати за зростанням елементи першого й останнього рядків рядка та поміняти їх місцями.
Шляхом послідовної перестановки рядків і стовпчиків розташувати найбільший елемент матриці А в правому верхньому куті, а найменший – в лівому нижньому.
З квадратної матриці А одержати нову матрицю так, щоб сума елементів кожного рядка зростав від першого рядка до останньої.
У квадратній матриці А впорядкувати елементи побічної діагоналі за зростанням, попередньо розділивши її елементи на центральний елемент матриці.
У квадратній матриці Е поміняти місцями елементи головної і побічної діагоналей, попередньо впорядкувавши побічну діагональ за спаданням елементів.
Дано квадратну матрицю А. Переставити стовпчики в матриці таким чином, щоб кількість елементів більших k зростало від першого стовпчика до останнього.
Нормувати вихідну матрицю B шляхом ділення елементів кожного стовпчика на найбільший елемент цього стовпчика.
З матриці А одержати нову матрицю, у якій рядки розташовані за спаданням елементів першого стовпчика.
Дано квадратну матрицю А. Одержати нову матрицю, у якій стовпчики розташовуються за спаданням елементів головної діагоналі.
Дано квадратну матрицю Q. З цієї матриці одержати нову матрицю Е, в якій рядки розташовані за спаданням елементів побічної діагоналі.
З матриці А одержати матрицю, у якій стовпчики розташовані за спаданням елементів першого рядка.
З матриці В одержати нову матрицю шляхом розташування стовпчиків таким чином, щоб елементи k-й рядка зростали за модулем.
Дано матрицю Х розмірності m×n. Одержати нову матрицю R, у якій елементи побічної діагоналі й останнього рядка переставлені місцями, попередньо впорядкувавши елементи діагоналі за спаданням.
Дано матрицю А розмірності m×n. Одержати нову матрицю М, у якій елементи першого й останнього стовпчика переставлені місцями, попередньо впорядкувавши перший стовпчик за спаданням, а останній – за зростанням.
З квадратної матриці А розмірності r×r одержати нову матрицю В, у якій стовпчик із найменшим за модулем елементом упорядкований за спаданням.
Контрольні запитання
Як здійснити введення та виведення багатомірних масивів інформації?
Який вигляд має алгоритм визначення найбільшого (найменшого) елемента масиву?
Який вигляд мають алгоритми сортування елементів масиву інформації?
Які способи опису масивів інформації?
Які операції виконуються над масивами інформації?
Який вигляд має алгоритм скалярного множення векторів?
Який вигляд має алгоритм множення матриці на вектор?
Який вигляд має алгоритм множення двох матриць?
Який вигляд має алгоритм перестановки елементів основної та побічної діагоналі в квадратній матриці?
Який вигляд має алгоритм перестановки елементів вказаного стовпчика і основної діагоналі квадратної матриці?
Який вигляд має алгоритм транспонування матриці?
Який вигляд має алгоритм обчислення визначника матриці розмірністю 2×2?
Який вигляд має алгоритм обчислення визначника матриці розмірністю 3×3?
Як вигляд має алгоритм визначення мінору матриці M2,4розмірністю 4×4?
ЛАБОРАТОРНА РОБОТА 10
ПРОЦЕДУРИ І ФУНКЦІЇ У МОВІ PASCAL
Мета роботи: набути практичні навички розробки алгоритмів і програм з використанням функцій та процедур.
Робоче завдання
Розробити алгоритм та скласти програму, що виконують:
виведення заголовка лабораторної роботи, у якому вказується найменування лабораторної роботи, її номер, варіант індивідуального завдання, прізвище студента та навчальна група;
введення початкових даних;
виконання дій, що вказані в умові індивідуального завдання;
виведення початкових даних та результатів обчислення.
Варіанти індивідуальних завдань для виконання лабораторної роботи
Таблиця 3
Номер варіанта
|
Умова задачі
|
Примітка
|
1
|
Обчислити і представити у виді векторів кількість від'ємних елементів кожного стовпчика матриць
A(n ,m), B(l ,k).
|
n, m, l, k 15
|
2
|
Обчислити суми і кількість елементів, що знаходяться в інтервалі від а до в для матриць
X(n ,m) і Y(d ,c).
|
n, m, d, c 20
|
3
|
Перетворити масиви А(m) і У(n), розташувавши в них підряд тільки додатні елементи. Замість інших елементів записати нулі.
|
n, m 50
|
4
|
Обчислити корені квадратних рівнянь x2- ax + b = 0 і
cz2- dz - f = 0.
|
|
5
|
Обчислити Z=(Xml+Xm2)/2, де Xml, Xm2 – найменші елементи масивів X1(l), X2(k).
|
L, k 100
|
6
|
Визначити сторони трикутників, заданих координатами їх вершин А(X1,Y1), У(X2 ,Y2), С(X3,Y3) і А1(X4,Y4), В1(X5,Y5), С1(X6,Y6).
|
Довжини сторін трикутників обчислити в процедурі
|
7
|
Обчислити суми елементів головних діагоналей матриць X(n ,n) і У(m ,m).
|
N, m 25
|
8
|
Визначити середнє значення і максимальне відхилення від середнього значення елементів масивів А(m), У(n).
|
N, m 100
|
Продовження таблиці 3
9
|
Обчислити Z=(S1+S2)/(K1+K2),де S1 і K1 – сума і кількість додатніх елементів масиву У(n),
S2 ,K2 – відповідно A(l).
|
N, l 50
|
10
|
Обчислити суми елементів верхньої трикутної матриці (з врахуванням діагоналей) для матриць
X(n, n) і Y(m, m).
|
N, m 10
|
11
|
Обчислити Z=(eS1+eS2)/(k1+k2), де S1, k1 – сума і кількість від'ємних елементів масиву A(n),
S2,k2 – сума і кількість елементів масиву B(m).
|
N, m 30, при (k1+k2)=0 вивести відповідну інформативу
|
12
|
Визначити кількість точок, що знаходяться всередині кола радіусом r із центром на початку координат. Координати точок задані векторами X(m) і Y(n).
|
N, m 50. Відстань до центру кола визначити в процедурі
|
13
|
Обчислити Z=(S1+S2)/2 де S1 – сума додатніх елементів основної діагоналі матриці A(n ,n), а S2 – побічної діагоналі.
|
N 100. Суми визначити в процедурі
|
14
|
Обчислити суми елементів більших d кожного рядка матриць X(n ,m) і Y(l , k).
|
N, m, l 10
|
15
|
Визначити кількість елементів матриць D(n ,m)
і R(c ,d), що менше а і більше в.
|
n, m, c, l 12
|
16
|
Обчислити мінори матриці W(h ,h)
|
h 10
|
17
|
Визначити число і суму додатніх елементів до першого від'ємного в масивах A(n , l), B(c ,k), D(r ,s).
|
N, c, l, k, r,
s 10
|
18
|
Обчислити Z=(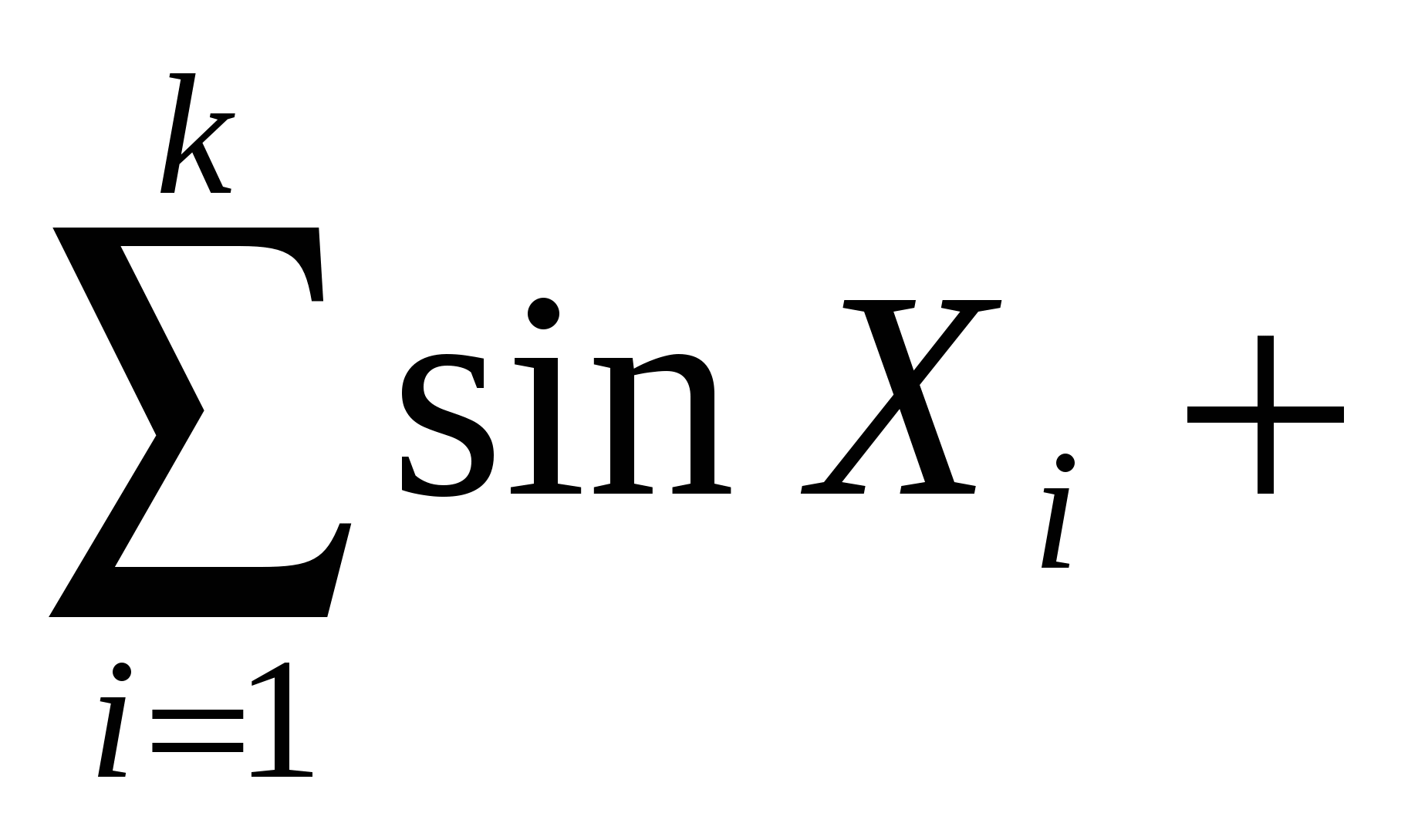 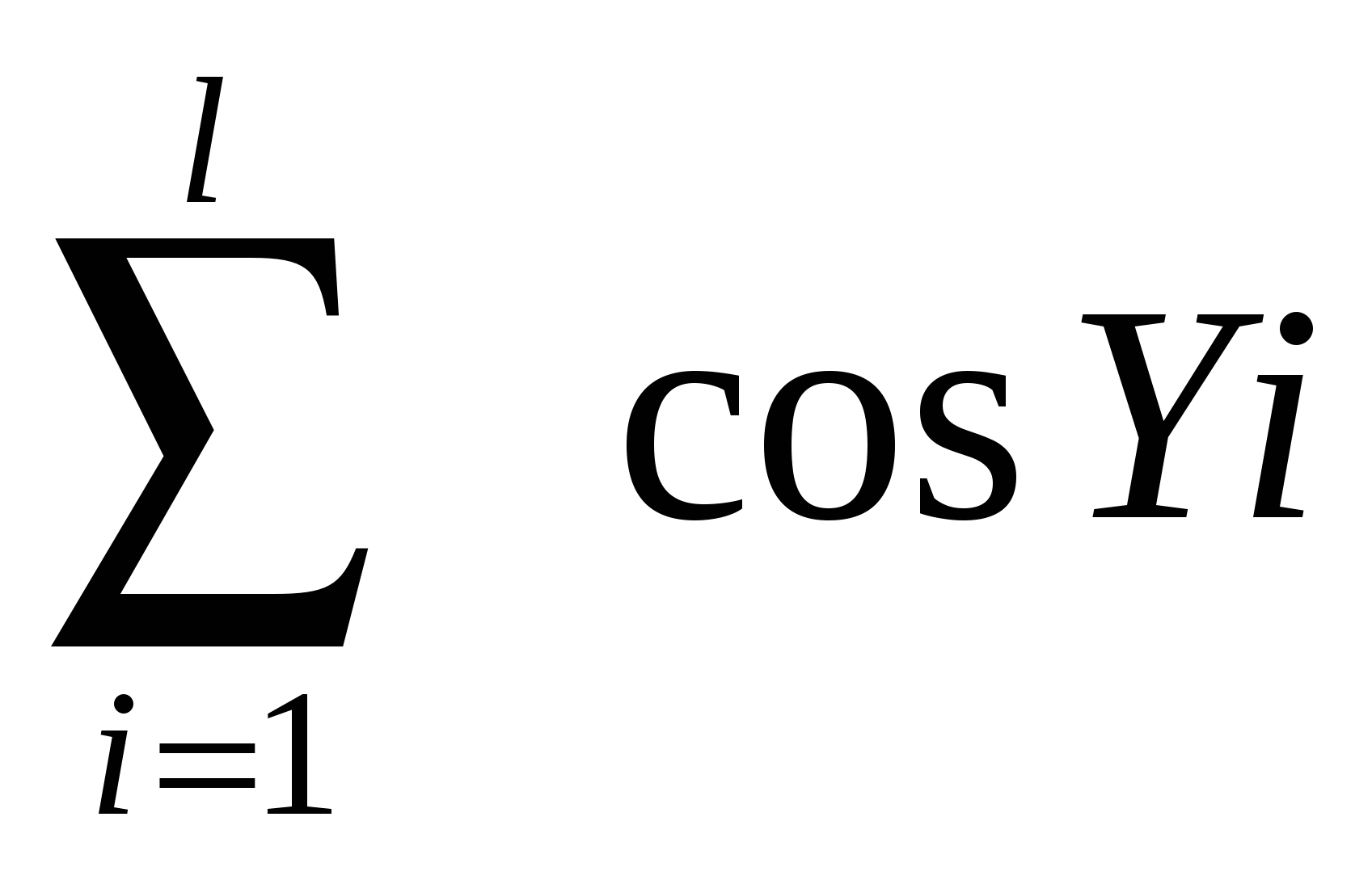 ) / ) /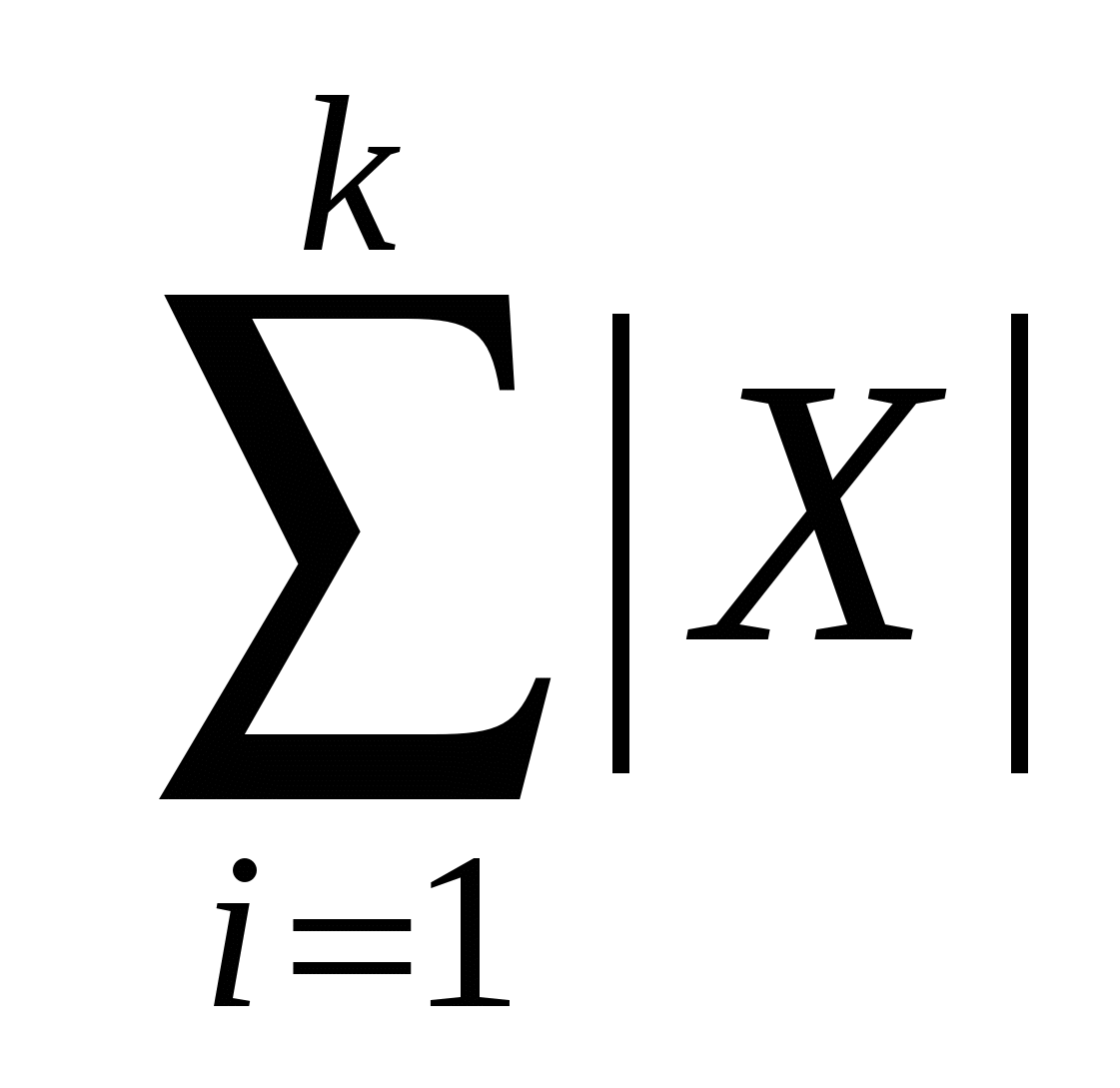 , ,
де Xi, Yi – відповідно елементи масивів X(k) і Y(l).
|
L, k 100
|
19
|
Визначити кількість елементів матриць A(n, m),
B(l, d) і C(r, s) більших q і менших x.
|
L, d, r, s 10, x>q
|
20
|
Вивести на друк вектори, складені з елементів цілочислових матриць A(n, m) і B(c, d) кратні l.
|
N, c, d, m 15,
l – ціле
|
21
|
Обчислити середнє арифметичне елементів більших a і менших b для масивів D(n,l), C(m,r) і K(x,y).
|
a < b, n, l, m, r, x,
y 10
|
22
|
Переписати додатні елементи масивів X(n) і Y(m) у масиви R і Z підряд.
|
N, m 50
|
23
|
Обчислити суми додатніх елементів масивів A(m), B(n) і C(k) і їх кількостей.
|
N, m, k 10
|
24
|
Обчислити Z=(а1+а2+а3)/3, де a1, a2, a3 – об’єми куль з радіусами r1, r2, r3 відповідно.
|
|
Продовження таблиці 3
25
|
Визначити найбільші елементи масивів A(n,m) і B(l,k) і поміняти їх місцями.
|
N, m, k, l ≤ 12
|
26
|
Обчислити d = (x1 - y1)(x2 + y2), де x1, y1, x2, y2– корені рівнянь a1x2+b1x+c1 = 0 та a2x2+b2x+c2 = 0.
|
|
27
|
Визначити кількість точок, що знаходяться всередині кола радіусом r із центром у точці з координатами (a, b). Координати точок задані масивами X(m) і Y(m).
|
M ≤ 20
|
28
|
Обчислити й представити у вигляді векторів суми позитивних елементів кожного рядка матриць A(m, n), B(k, r).
|
M, k, n, r 15
|
29
|
Обчислити суму елементів нижніх трикутних матриць
(з врахуванням діагональних елементів) для матриць
A(m, m), B(n, n).
|
M, n 10
|
30
|
Обчислити суму діагональних елементів, що більше а і менше b для матриць C(m, m), B(n, n).
|
M, n 15, a
|
|
 Скачать 1.84 Mb.
Скачать 1.84 Mb.