Інженерна графіка 1. Методичні вказівки до виконання практичних завдань
 Скачать 8.05 Mb. Скачать 8.05 Mb.
|
|
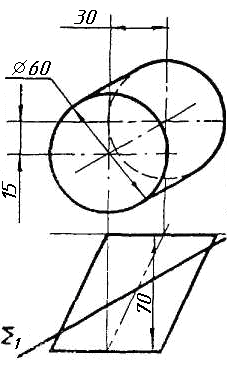
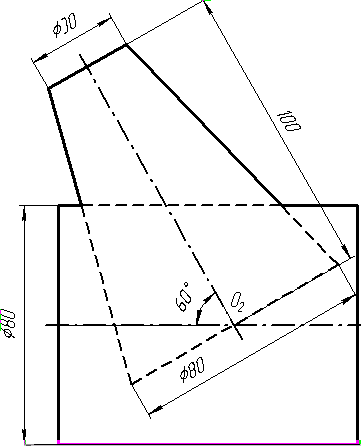
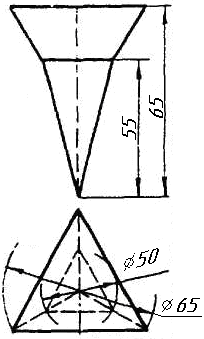
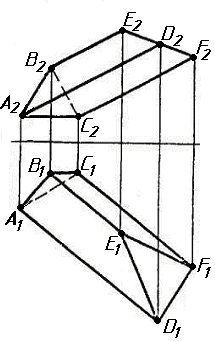
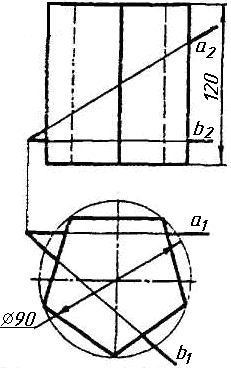
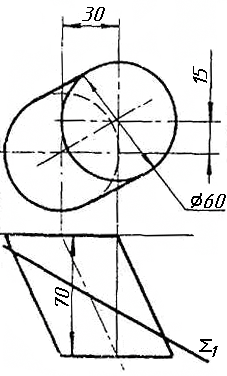
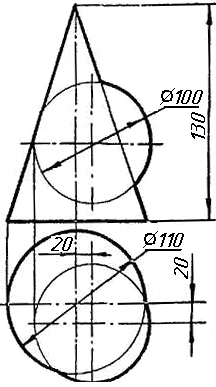
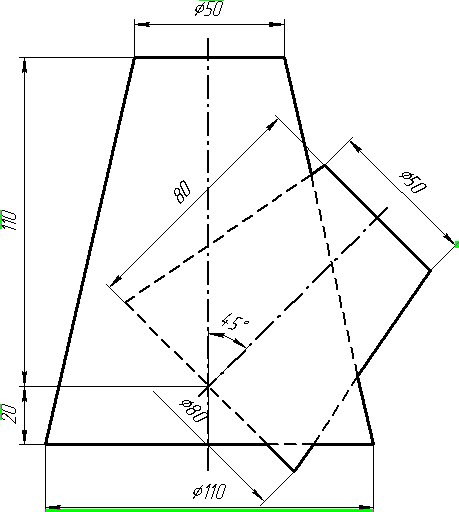
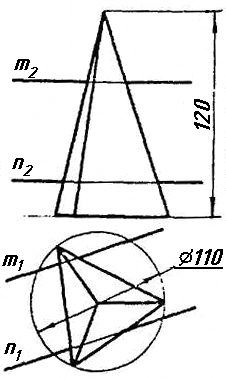
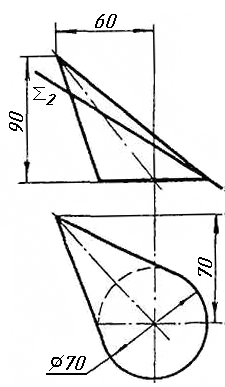
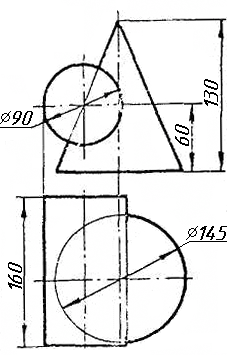
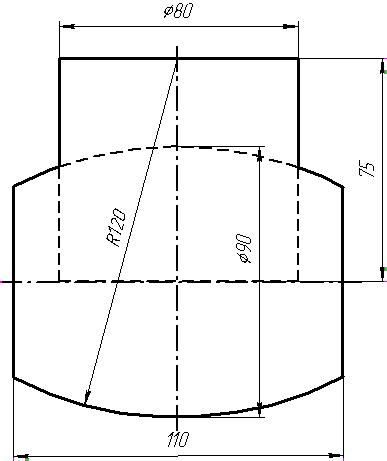
Задача 4. Через пряму АВ провести площину, перпендикулярно до заданої площини Р (CD; СE). Побудувати лінію перетину двох площин. Задача 5. Визначити відстань від вершини A до грані CBEF призми методом заміни площин проекцій. Задача 6. Визначити кут між гранями ABS та BCS піраміди методом плоско-паралельного переміщення. Задача 7. Визначити натуральну величину кута між прямою l та площиною Р (m || n) методом обертання навколо прямої рівня. Задача 8. Побудувати переріз призми площиною загального положення. Задача 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу. Задача 10. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на обох проекціях. Задача 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.
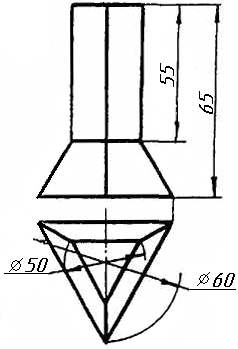
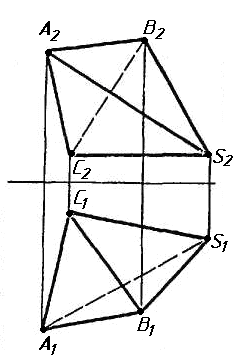
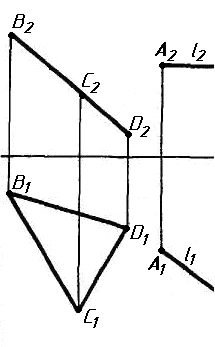
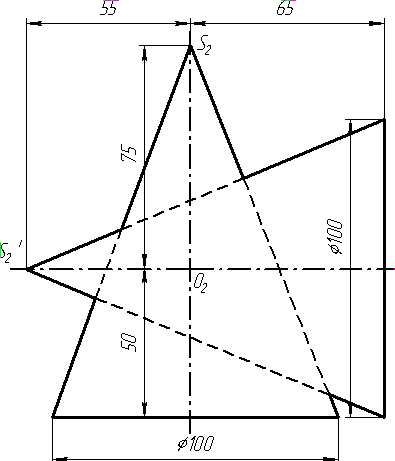
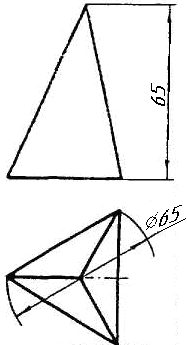
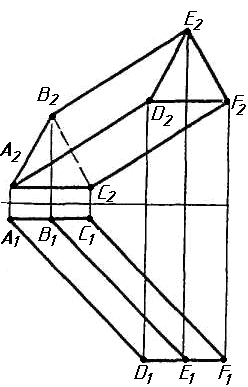
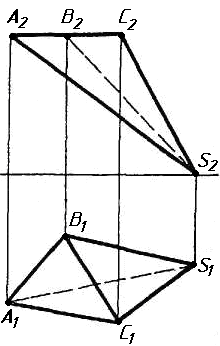
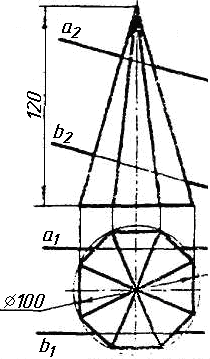
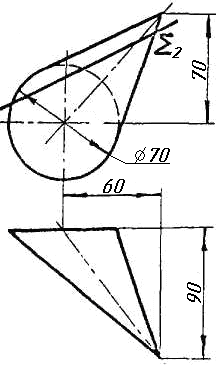
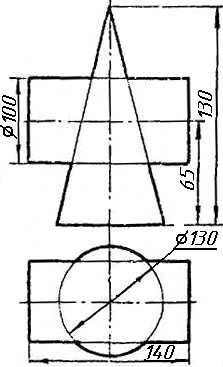
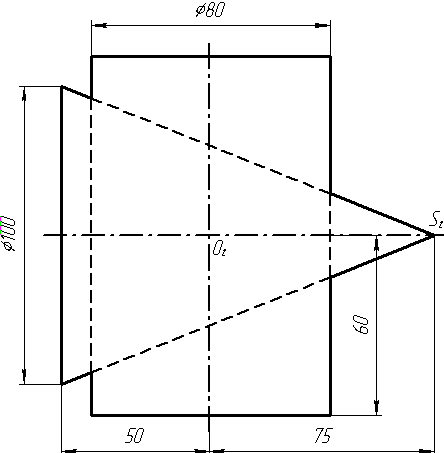
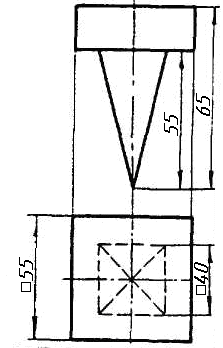
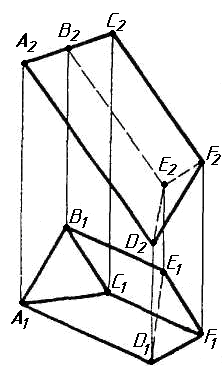
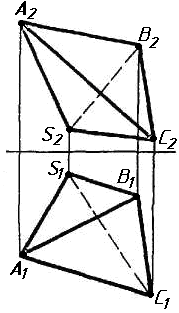
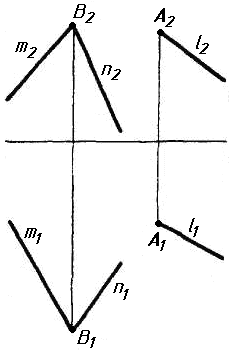
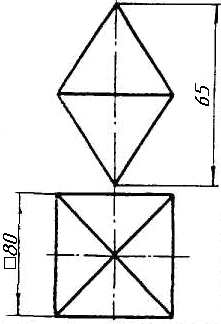
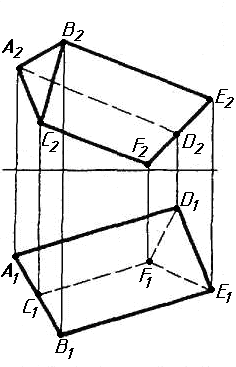
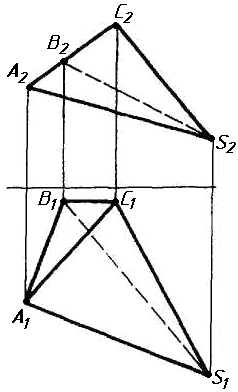
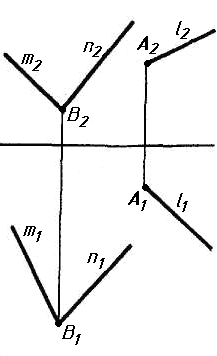
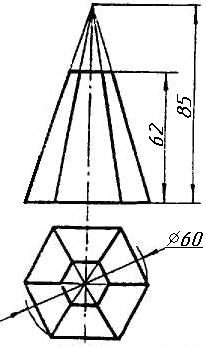
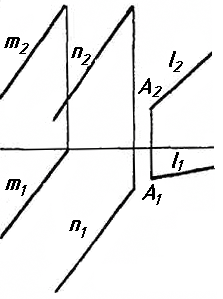
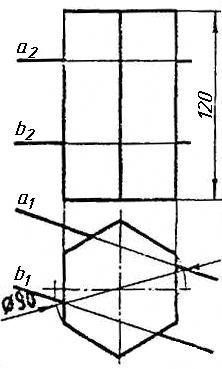
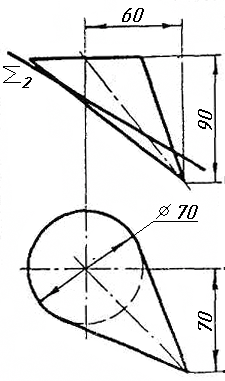
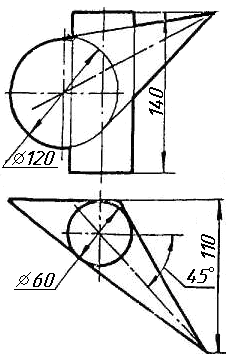
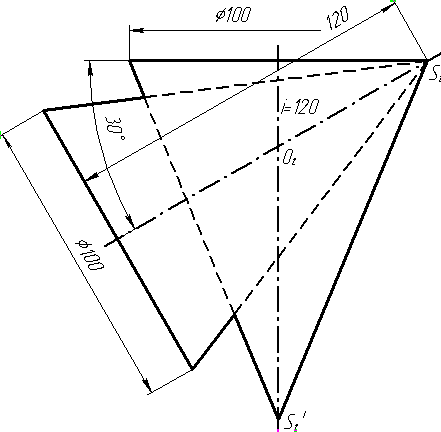
Задача 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити. Задача 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій та побудувати його сліди. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій. Задача 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій. Задача 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині (АВ; ВС). Задача 4. Через пряму АВ провести площину, перпендикулярно до заданої площини Р ( CDE). Побудувати лінію перетину двох площин. Задача 5. Визначити кут між гранями ABED та CBEF призми методом заміни площин проекцій. Задача 6. Визначити відстань між ребрами AB та CS призми методом плоско-паралельного переміщення. Задача 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня. Задача 8. Побудувати переріз призми площиною загального положення. Задача 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу. Задача 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях. Задача 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.
Задача 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити. Задача 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій та побудувати його сліди. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій. Задача 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій. Задача 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині (АВ; С). Задача 4. Через пряму АВ провести площину, перпендикулярно до заданої площини ( CDE). Побудувати лінію перетину двох площин. Задача 5. Визначити кут між гранями BADE та CADF призми методом заміни площин проекцій. Задача 6. Визначити відстань від вершини S до ребра BC піраміди методом плоско-паралельного переміщення. Задача 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня. Задача 8. Побудувати переріз піраміди площиною загального положення. Задача 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу. Задача 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях. Задача 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.
Задача 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити. Задача 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій та побудувати його сліди. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій. Задача 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій. Задача 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині (АВ; ВС). Задача 4. Через пряму АВ провести площину, перпендикулярно до заданої площини ( CDE). Побудувати лінію перетину двох площин. Задача 5. Визначити кут між гранями ABED та CBEF призми методом заміни площин проекцій. Задача 6. Визначити відстань від вершини S до ребра BC піраміди методом плоско-паралельного переміщення. Задача 7. Визначити натуральну величину кута між прямою l та площиною P ( BCD) методом обертання навколо прямої рівня. Задача 8. Побудувати переріз піраміди площиною загального положення. Задача 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу. Задача 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях. Задача 11. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на двох проекціях.
Задача 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити. Задача 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій та побудувати його сліди. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій. Задача 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій. Задача 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині ( АВС). Задача 4. Через пряму АВ провести площину, перпендикулярно до заданої площини ( CDE). Побудувати лінію перетину двох площин. Задача 5. Визначити відстань між ребрами AD та BE призми методом плоско паралельного переміщення. Задача 6. Визначити кут між гранями ABS та ABC піраміди методом плоско-паралельного переміщення. Задача 7. Визначити натуральну величину кута між прямою l та площиною P (m X n) методом обертання навколо прямої рівня. Задача 8. Побудувати переріз призми площиною загального положення. Задача 9. Побудувати переріз похилого циліндра площиною та розгортку його бічної поверхні з нанесенням лінії перерізу. Задача 10. Побудувати лінію взаємного перетину конуса та сфери. Визначити її видимість на обох проекціях. Задача 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях.
Задача 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити. Задача 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій та побудувати його сліди. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій. Задача 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій. Задача 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині (АВ; ВС). Задача 4. Через пряму АВ провести площину, перпендикулярно до заданої площини Р (CЕ; D). Побудувати лінію перетину двох площин. Задача 5. Визначити кут між гранями ABED та BEFC призми методом заміни площин проекцій. Задача 6. Визначити відстань між ребрами AC та BS піраміди методом плоско-паралельного переміщення. Задача 7. Визначити натуральну величину кута між прямою l та площиною Р (m Х n) методом обертання навколо прямої рівня. Задача 8. Побудувати переріз піраміди площиною загального положення. Задача 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу. Задача 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях. Задача 11. Побудувати лінію взаємного перетину циліндра та тора. Визначити її видимість на двох проекціях.
Задача 0. За даними двома проекціями багатогранника побудувати його профільну проекцію та ізометрію. Вершини багатогранника позначити. Задача 1. Побудувати проекції похилої призми з паралельними основами за координатами вершин основи, спрямуванням бічного ребра АК та його натуральній величині, що дорівнює 100 мм. Визначити кути нахилу ребра АК до площин проекцій та побудувати його сліди. Визначити видимість. Проаналізувати розташування ребер відносно площин проекцій. Задача 2. Побудувати проекції піраміди, якщо відомо, що точка К належить грані ABS. Проаналізувати розташування граней піраміди відносно площин проекцій. Задача 3. Добудувати відсутню проекцію трикутника ELQ, який належить площині , що проходить через точку К паралельно площині (А, В, С). Задача 4. Через пряму АВ провести площину, перпендикулярно до заданої площини ( CDE). Побудувати лінію перетину двох площин. Задача 5. Визначити кут між гранями BEDA та BEFC призми методом заміни площин проекцій. Задача 6. Визначити відстань між ребрами AB та SC піраміди методом плоско-паралельного переміщення. Задача 7. Визначити натуральну величину кута між прямою l та площиною Р (m || n) методом обертання навколо прямої рівня. Задача 8. Побудувати переріз призми площиною загального положення. Задача 9. Побудувати переріз похилого конуса площиною та розгортку його бічної поверхні з нанесенням лінії перерізу. Задача 10. Побудувати лінію взаємного перетину конуса та циліндра. Визначити її видимість на обох проекціях. Задача 11. Побудувати лінію взаємного перетину двох конусів. Визначити її видимість на двох проекціях. Додаток 1. Приклад виконання титульного аркуша  Додаток 2. Приклад написання українських літер згідно з ГОСТ 2.304-81  Додаток 3. Приклад виконання та заповнення основного напису 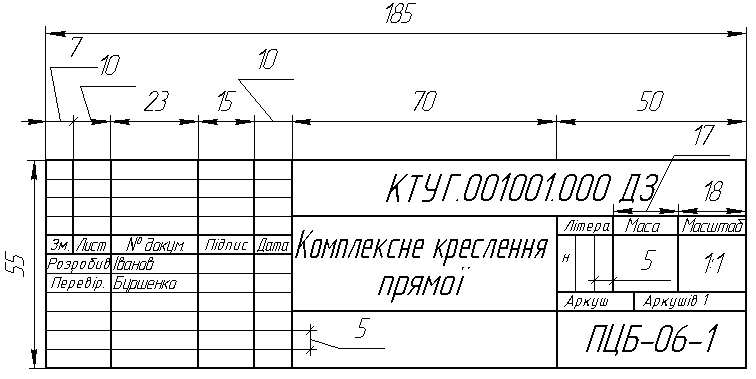 КТУГ – чотиризначний код організації-розробника. Складається з абревіатури назви університету (КТУ) та абревіатури назви кафедри (графіки - Г). 001 001 – код класифікаційної характеристики. Перші 3 цифри – номер варіанту, а наступні 3 – номер завдання. ДЗ – код неосновного конструкторського документу. ДЗ – домашнє завдання (АР – аудиторна робота). Додаток 4. Приклад білету контрольно-модульної роботи № 1 БІЛЕТ № 71. Побудувати лінію перетину площин 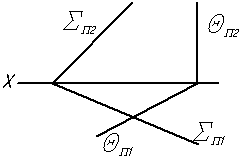 2. Визначити відстань від точки А до 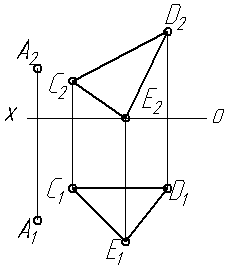 3. Через точку А провести площину 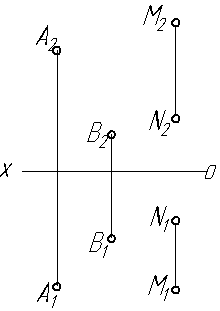 Додаток 5. Приклад білету контрольно-модульної роботи № 2 БІЛЕТ № 3
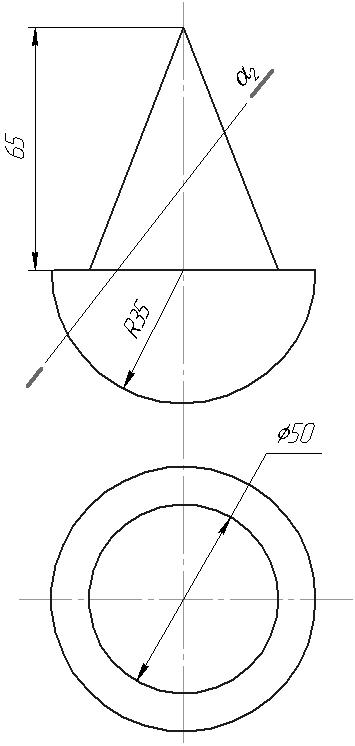 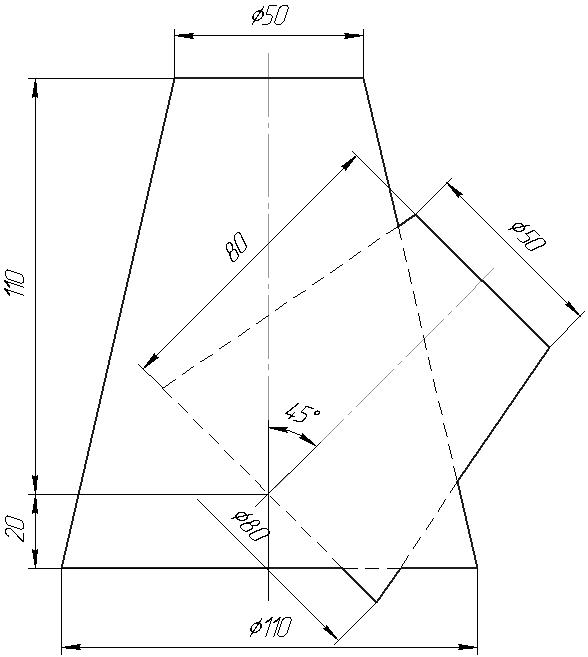 1 2 ЛІТЕРАТУРА
Методичні вказівки до виконання практичних завдань з дисципліни “Інженерна графіка” для студентів з напряму підготовки “Будівництво” усіх форм навчання (I частина) УКЛАДАЧІ: Наталія Петрівна Мельниченко Ольга Петрівна Буршенко Реєстраційний № ___ Підписано до друку _________________ Формат А4 Обсяг 45 сторінок Тираж ___ примірників Видавничий центр КТУ, м. Кривий Ріг, вул..ХХП партз’їзду, 11 |