ДИПЛОМ 2020 года.. Методика оценки изменений климатических

• Название: Методика оценки изменений климатических
• Дата: 06.03.2022
• Размер: 1.63 Mb.
• Имя файла: ДИПЛОМ 2020 года..doc
• Тип: Пояснительная записка; #384963
• страница: 8 из 11

3. МЕТОДИКА ПРОГНОЗИРОВАНИЯ КЛИМАТИЧЕСКИХ
ИЗМЕНЕНИЙ

3.1. Использование классических физико-статистических методов
прогнозирования

Взаимосвязь между метеовеличинами может быть описана разными способами. Например, эту связь можно описать с помощью различных коэффициентов корреляции (линейных, частных, корреляционного отношения). Эту связь можно выразить как зависимость между аргументом X и функцией Y. В этом случае задача будет состоять в нахождении регрессии – зависимости вида Y=f(X) или вида X=f(Y) [15].

Графическое выражение регрессионного уравнения называют линией регрессии. Линия регрессии выражает наилучшее предсказание зависимой переменной Y по независимым переменным X [9].

Регрессию обычно выражают с помощью уравнения регрессии, которое в самом простом случае выглядят, как уравнение прямой, а именно:

(3.1)

где – зависимая переменная; – независимая переменная; свободный член; – коэффициент регрессии, определяющий наклон линии регрессии по отношению к осям координат.

На рисунке 3.1 приведен общий вид линейной регрессии.

При наличии между метеовеличинами нелинейные соотношений, они выражаются с помощью соответствующих нелинейных функций, например: равносторонняя гипербола, парабола второй степени и др.

Существует несколько видов нелинейной регрессии.

Гиперболическое уравнение регрессии:

.

(3.2)

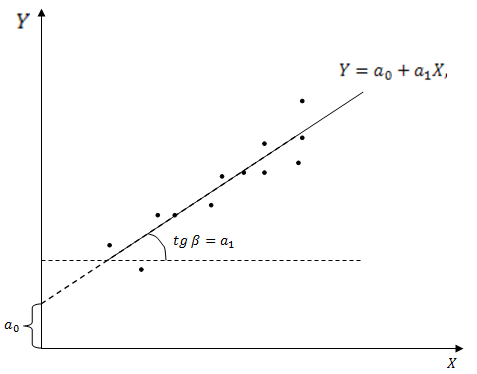
Рис.3.1. Общий вид линейной регрессии
Логарифмическое уравнение регрессии:

.

(3.3)

Обратное уравнение регрессии:

.

(3.4)

Степенное уравнение регрессии:

.

(3.5)

Экспоненциальное уравнение регрессии:

.

(3.6)

Основное свойство нелинейной регрессии заключается в том, что увеличение/уменьшение значений зависимой переменной происходит непропорционально увеличению/уменьшению независимой переменной [8].

Один из методов представления регрессий, в которых зависимая переменная линейно связана с параметрами, являются полиномы m-й степени (формула 3.7).

.

(3.7)

При оценке параметров нелинейных регрессий используется метод замены переменных. Суть его состоит в замене нелинейных переменных новыми линейными переменными, в результате чего нелинейная регрессия сводится к линейной. Но стоит учитывать, что данный метод применим только для уравнений, нелинейных по переменным; для существенно нелинейных переменных данный метод неприменим [9].

Имея необходимую выборку метеовеличин, для которых нужно провести регрессионный анализ, можно воспользоваться различными прикладными программами, одной из которых является Microsoft Excel.