Главная страница
Навигация по странице:

  • 3.3. Разработка прогноза на основе современных методов анализа данных

    		•

    ДИПЛОМ 2020 года.. Методика оценки изменений климатических


    Скачать 1.63 Mb.
    НазваниеМетодика оценки изменений климатических
    Дата06.03.2022
    Размер1.63 Mb.
    Формат файлаdoc
    Имя файлаДИПЛОМ 2020 года..doc
    ТипПояснительная записка
    #384963
    страница9 из 11
    1   2   3   4   5   6   7   8   9   10   11

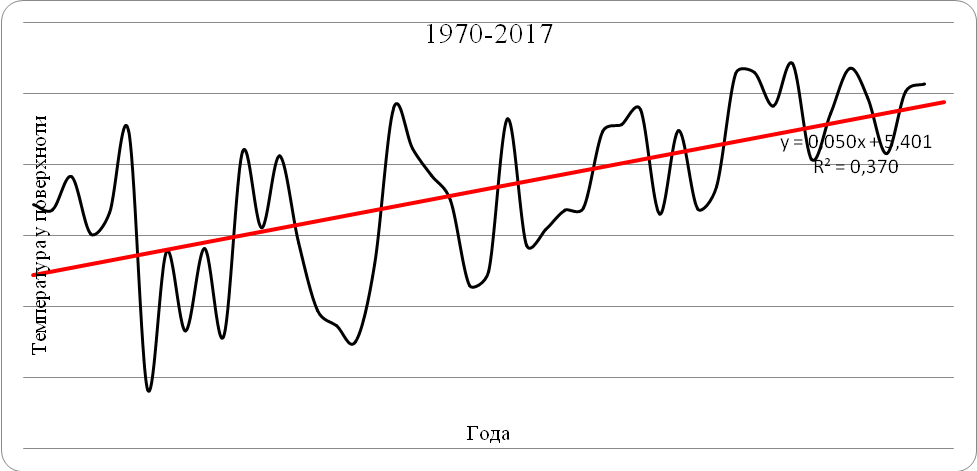
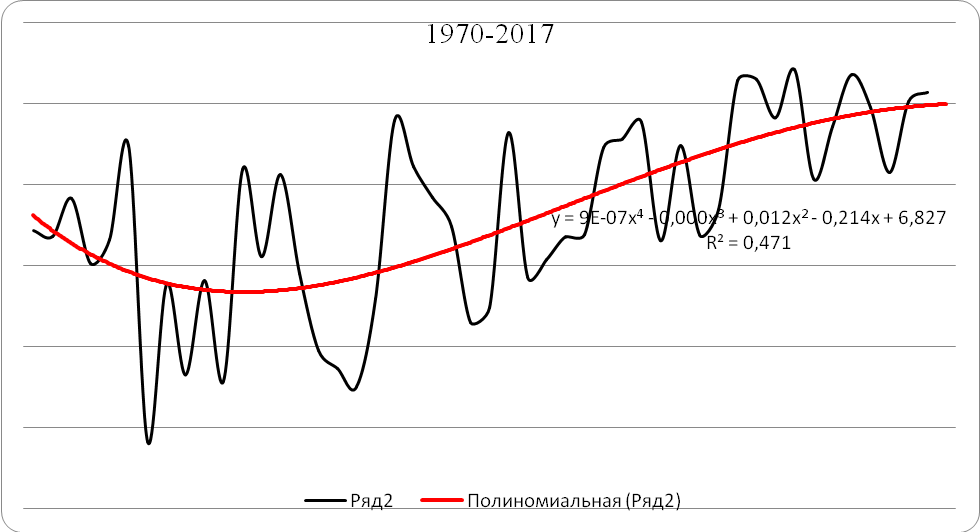
    3.2. Анализ годового хода температуры и определение величины
    тренда


    Земная климатическая система характеризуется изменчивостью, в том числе с временными масштабами от нескольких лет до нескольких десятилетий. Полный анализ изменений климата должен учитывать взаимодействие между различными климатическими модами.

    Одной из характерных особенностей глобального потепления по данным для приповерхностной температуры является общее уменьшение амплитуды годового хода. Эта тенденция воспроизводится климатическими моделями, в том числе при глобальном потеплении, вследствие увеличения содержания CO2 в атмосфере. Температурные изменения, в том числе изменения характеристик годового хода, в разных слоях атмосферы зависят от типа глобальных климатических изменений, в частности, от типа антропогенных воздействий и относительной роли естественных и антропогенных вариаций климата. При этом тенденции изменения характеристик годового хода температуры разных атмосферных слоев в разных регионах могут служить дополнительным индикатором общих изменений климата и использоваться при тестировании моделей и для диагностики процессов климатических изменений [ССЫЛКА].

    При изучении изменения климата, прежде всего, исследуются колебания во времени температуры воздуха. Одной из причин этого является то, что по этому элементу накоплены наиболее длинные и достоверные ряды наблюдений. Это дает возможность проанализировать колебания климата, происшедшие за последние годы.

    Временной ряд температуры представляет собой совокупность данных, описывающих объект в последовательные моменты времени. Анализ временных рядов основывается на предположении, что последовательные данные наблюдаются через равные промежутки времени.

    Большинство временных рядов делятся на два класса: они являются либо трендом, либо сезонной составляющей.

    Тренд (от англ. Trend–тенденция) – основная тенденция изменения временного ряда. Тренды могут быть описаны различными уравнениями –линейными, логарифмическими, степенными и т.д. Фактический тип тренда устанавливают на основе подбора его функциональной модели статистическими методами либо сглаживанием исходного временного ряда.

    При построении тренда учитывается его монотонность, или наоборот, содержание во временном ряде многочисленных ошибок. В первом случае анализировать ряд не составляет труда. Если же во временном ряду имеются значительные ошибки, тренд необходимо сгладить. Сглаживание включает в себя осреднение данных.

    В анализе временных рядов существуют два основных метода оценки тренда: параметрические и непараметрические.

    Параметрические методы рассматривают временной ряд как гладкую функцию ,где . При этом сначала выявляют один либо несколько допустимых типов функций ; затем различными методами оценивают параметры этих функций, после чего выбирают окончательную модель тренда [13].

    Непараметрическими являются такие методы сглаживания исходного временного ряда, как метод скользящих средних, метод экспоненциального сглаживания и др.

    На рисунках 3.2 и 3.3 представлены примеры построения тренда с использование линейного и полиномиального уравнений.



    Рис. 3.2. Сглаживание ряда среднегодовой температуры воздуха линейной регрессией


    Рис. 3.3. Сглаживание ряда среднегодовой температуры воздуха полиномом 3-й степени

    3.3. Разработка прогноза на основе современных методов анализа
    данных


    Для анализа и разработки прогноза среднегодовых значений метеовеличин необходимо использовать архивные данные. При выполнении работы была сформирована архивная выборка данных о температуры в г. Воронеже сроком с 1970 по 2017 года включительно. Фрагмент архивной выборки представлен на рисунке 3.2.



    Рис. 3.2. Фрагмент архивной выборки
    По сформированной выборке были рассчитаны средние значения температуры за день, декаду, месяц, год (рисунки 3.3–3.6).


    Рис. 3.3. Фрагмент средних значений температуры за день по г. Воронеж


    Рис. 3.4. Фрагмент среднедекадных значений температуры по г. Воронеж


    Рис. 3.5. Фрагмент средних месячных значений температуры по г. Воронеж


    Рис. 3.6. Полученные среднегодовые значений температуры по г. Воронеж
    После формирования архивной выборки был проведен ее анализ: были выявлены самые теплые и самые холодные года, а также получены иные необходимые результаты.

    Далее по сформированной выборке были построены линейная регрессия и полиномы разных степеней (от 2 до 6) (рисунки 3.7 – 3.12).


    Рис. 3.7. Сглаживание ряда среднегодовой температуры воздуха полиномом 2-й степени


    Рис. 3.8. Сглаживание ряда среднегодовой температуры воздуха полиномом 3-й степени


    Рис. 3.9. Сглаживание ряда среднегодовой температуры воздуха полиномом 4-й степени


    Рис. 3.10. Сглаживание ряда среднегодовой температуры воздуха полиномом 5-й степени


    Рис. 3.11. Сглаживание ряда среднегодовой температуры воздуха полиномом
    6-й степени


    Рис. 3.12. Линейная регрессия
    Полиномы и линейная регрессия были построены с прогнозированием на один период вперед, чтобы сравнить прогностические данные с фактическими. В таблице 3.1 представлены ошибки прогностических значений в отличии от фактических данных, а также прогноз на 2018 год.
    Таблица 3.1

    Ошибки регрессионного анализа
    Года
    Фактические знач.
    Прогностические знач.
    Ошибка

    прогноза

    Полином 2-ой степени
    2016
    8,0
    8,4
    0,4

    2017
    8,1
    8,5
    0,4

    2018
    -
    8,5
    -

    Полином 3-ой степени
    2016
    8,0
    7,8
    0,2

    2017
    8,1
    7,9
    0,2

    2018
    -
    7,9
    -

    Полином 4-ой степени
    2016
    8,0
    7,8
    0,2

    2017
    8,1
    7,9
    0,2

    2018
    -
    8,0
    -

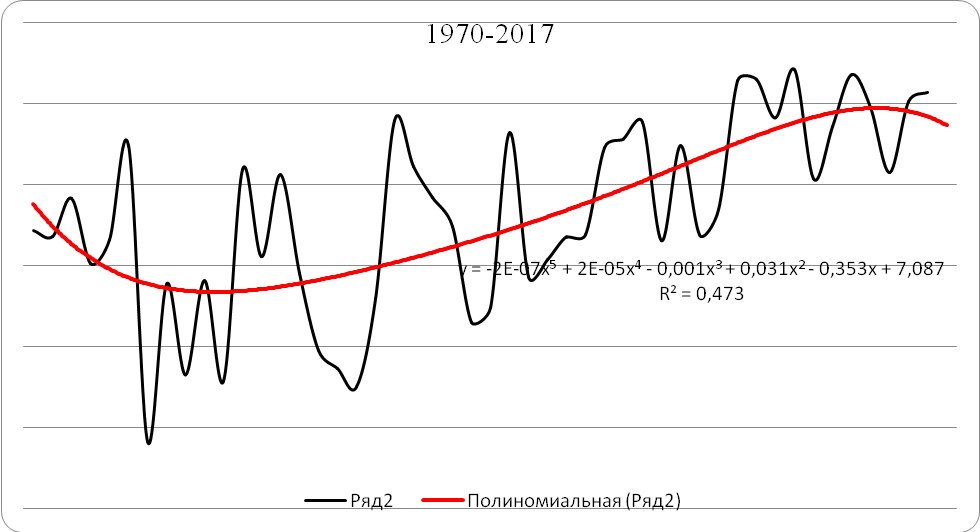
    Полином 5-ой степени
    2016
    8,0
    7,5
    0,5

    2017
    8,1
    7,7
    0,4

    2018
    -
    7,8
    -

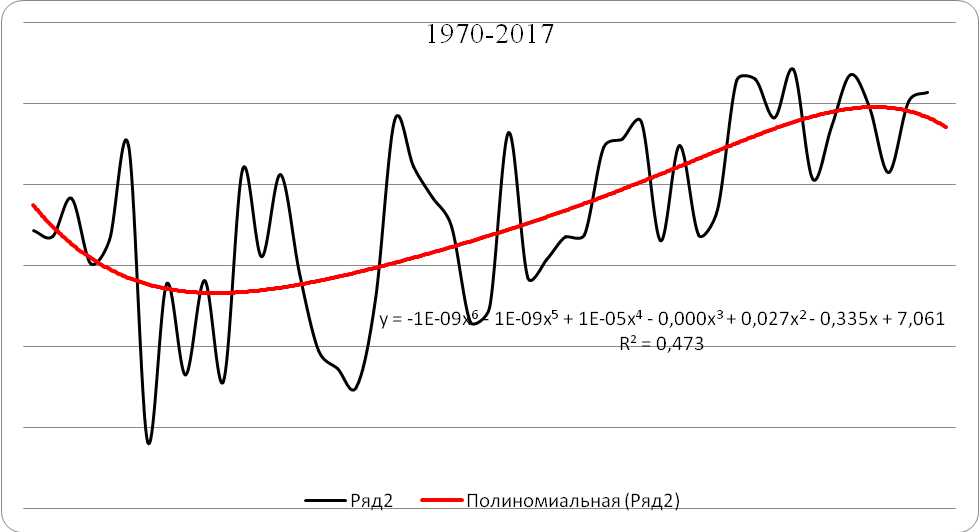
    Полином 6-ой степени
    2016
    8,0
    7,3
    0,7

    2017
    8,1
    7,7
    0,4

    2018
    -
    7,8
    -

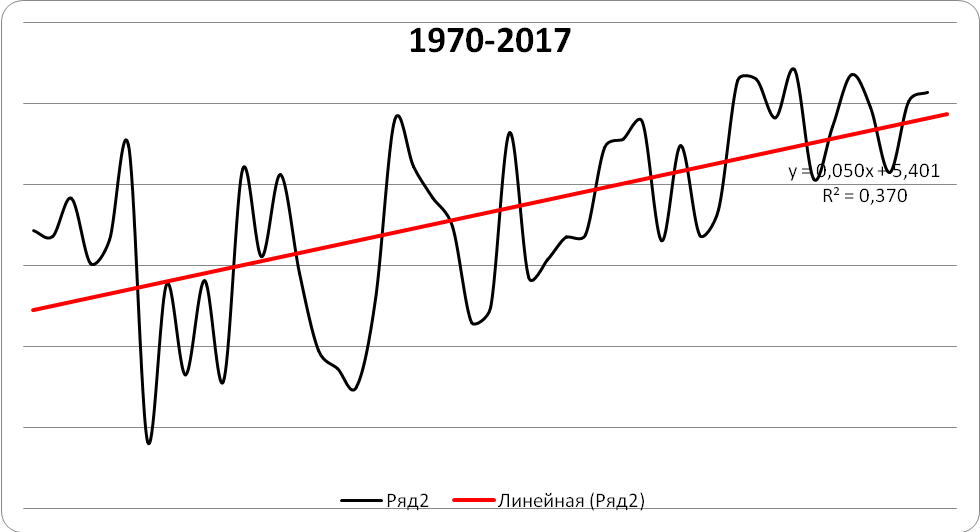
    Линейная регрессия
    2016
    8,0
    7,7
    0,3

    2017
    8,1
    7,8
    0,3

    2018
    -
    7,9
    -


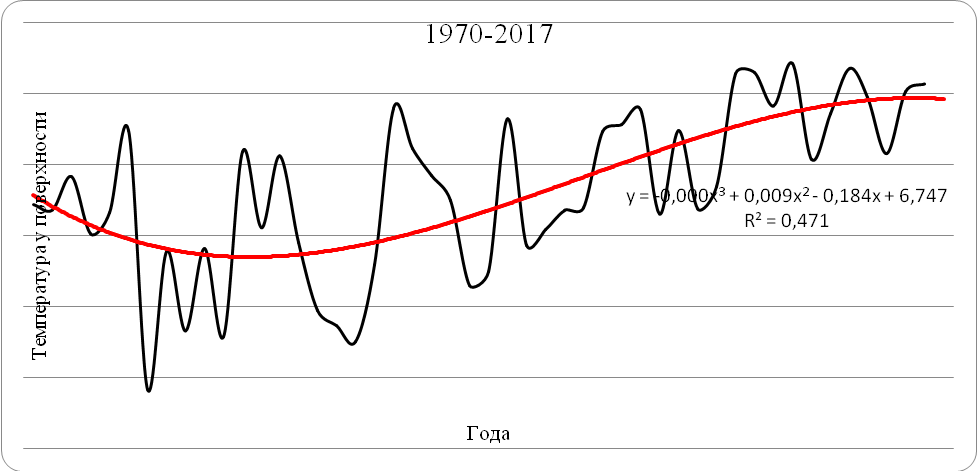
    Как видно из регрессионного анализа, самые незначительные ошибки (0,2°С) были у полиномов 3-й и 4-й степени, что является приемлемым значением.

    Помимо регрессионного анализа для прогноза тенденции температуры были исследованы возможности искусственных нейронных сетей. Для этого использовалась программа Neural Analizer, входящая в статистический пакет Deductor Academic.

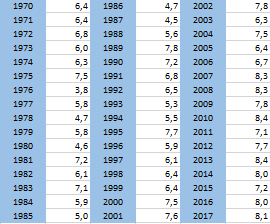
    С учетом известного одиннадцатилетнего периода колебаний температуры воздуха для прогнозирования температуры, выборка была составлена таким образом, что каждый 12-й год являлся прогнозом в своем ряду. Во втором ряду происходило смещение на одно значение.
    Таблица 3.2

    Выборка для прогнозирования среднегодовой температуры в искусственной
    нейронной сети

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    П

    6,4
    6,4
    6,8
    6,0
    6,3
    7,5
    3,8
    5,8
    4,7
    5,8
    4,6
    7,2

    6,4
    6,8
    6,0
    6,3
    7,5
    3,8
    5,8
    4,7
    5,8
    4,6
    7,2
    6,1

    6,8
    6,0
    6,3
    7,5
    3,8
    5,8
    4,7
    5,8
    4,6
    7,2
    6,1
    7,1

    6,0
    6,3
    7,5
    3,8
    5,8
    4,7
    5,8
    4,6
    7,2
    6,1
    7,1
    5,9

    6,3
    7,5
    3,8
    5,8
    4,7
    5,8
    4,6
    7,2
    6,1
    7,1
    5,9
    5,0

    7,5
    3,8
    5,8
    4,7
    5,8
    4,6
    7,2
    6,1
    7,1
    5,9
    5,0
    4,7

    3,8
    5,8
    4,7
    5,8
    4,6
    7,2
    6,1
    7,1
    5,9
    5,0
    4,7
    4,5

    5,8
    4,7
    5,8
    4,6
    7,2
    6,1
    7,1
    5,9
    5,0
    4,7
    4,5
    5,6

    4,7
    5,8
    4,6
    7,2
    6,1
    7,1
    5,9
    5,0
    4,7
    4,5
    5,6
    7,8

    5,8
    4,6
    7,2
    6,1
    7,1
    5,9
    5,0
    4,7
    4,5
    5,6
    7,8
    7,2

    4,6
    7,2
    6,1
    7,1
    5,9
    5,0
    4,7
    4,5
    5,6
    7,8
    7,2
    6,8

    7,2
    6,1
    7,1
    5,9
    5,0
    4,7
    4,5
    5,6
    7,8
    7,2
    6,8
    6,5

    6,1
    7,1
    5,9
    5,0
    4,7
    4,5
    5,6
    7,8
    7,2
    6,8
    6,5
    5,3

    7,1
    5,9
    5,0
    4,7
    4,5
    5,6
    7,8
    7,2
    6,8
    6,5
    5,3
    5,5

    5,9
    5,0
    4,7
    4,5
    5,6
    7,8
    7,2
    6,8
    6,5
    5,3
    5,5
    7,7

    5,0
    4,7
    4,5
    5,6
    7,8
    7,2
    6,8
    6,5
    5,3
    5,5
    7,7
    5,9

    4,7
    4,5
    5,6
    7,8
    7,2
    6,8
    6,5
    5,3
    5,5
    7,7
    5,9
    6,1

    4,5
    5,6
    7,8
    7,2
    6,8
    6,5
    5,3
    5,5
    7,7
    5,9
    6,1
    6,4

    5,6
    7,8
    7,2
    6,8
    6,5
    5,3
    5,5
    7,7
    5,9
    6,1
    6,4
    6,4

    7,8
    7,2
    6,8
    6,5
    5,3
    5,5
    7,7
    5,9
    6,1
    6,4
    6,4
    7,5

    7,2
    6,8
    6,5
    5,3
    5,5
    7,7
    5,9
    6,1
    6,4
    6,4
    7,5
    7,6

    6,8
    6,5
    5,3
    5,5
    7,7
    5,9
    6,1
    6,4
    6,4
    7,5
    7,6
    7,8

    6,5
    5,3
    5,5
    7,7
    5,9
    6,1
    6,4
    6,4
    7,5
    7,6
    7,8
    6,3

    5,3
    5,5
    7,7
    5,9
    6,1
    6,4
    6,4
    7,5
    7,6
    7,8
    6,3
    7,5

    5,5
    7,7
    5,9
    6,1
    6,4
    6,4
    7,5
    7,6
    7,8
    6,3
    7,5
    6,4

    7,7
    5,9
    6,1
    6,4
    6,4
    7,5
    7,6
    7,8
    6,3
    7,5
    6,4
    6,7

    5,9
    6,1
    6,4
    6,4
    7,5
    7,6
    7,8
    6,3
    7,5
    6,4
    6,7
    8,3

    6,1
    6,4
    6,4
    7,5
    7,6
    7,8
    6,3
    7,5
    6,4
    6,7
    8,3
    8,3

    6,4
    6,4
    7,5
    7,6
    7,8
    6,3
    7,5
    6,4
    6,7
    8,3
    8,3
    7,8

    6,4
    7,5
    7,6
    7,8
    6,3
    7,5
    6,4
    6,7
    8,3
    8,3
    7,8
    8,4

    7,5
    7,6
    7,8
    6,3
    7,5
    6,4
    6,7
    8,3
    8,3
    7,8
    8,4
    7,1

    7,6
    7,8
    6,3
    7,5
    6,4
    6,7
    8,3
    8,3
    7,8
    8,4
    7,1
    7,7

    7,8
    6,3
    7,5
    6,4
    6,7
    8,3
    8,3
    7,8
    8,4
    7,1
    7,7
    8,4

    6,3
    7,5
    6,4
    6,7
    8,3
    8,3
    7,8
    8,4
    7,1
    7,7
    8,4
    8,0

    7,5
    6,4
    6,7
    8,3
    8,3
    7,8
    8,4
    7,1
    7,7
    8,4
    8,0
    7,2

    6,4
    6,7
    8,3
    8,3
    7,8
    8,4
    7,1
    7,7
    8,4
    8,0
    7,2
    8,0

    6,7
    8,3
    8,3
    7,8
    8,4
    7,1
    7,7
    8,4
    8,0
    7,2
    8,0
    8,1


    По сформированной выборке была построена нейронная сеть, представленная на рисунке 3.13.


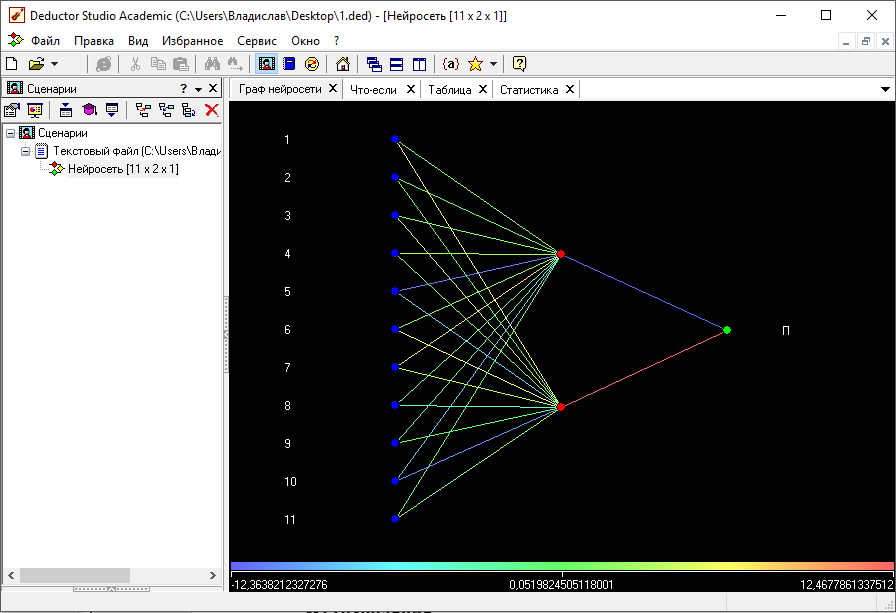
    Рис. 3.13. Граф нейросети
    Прогнозирование в нейросети программы Neural Analizer пакета Deductor Academic осуществляется в графе «Что если». Имея данные температуры за 11 предыдущих лет, ее можно спрогнозировать на последующий год. Значения необходимо вписать в соответствующие ячейки, идущие по порядку. После чего прогноз (выходное значение искусственной нейронной сети) автоматически поменяется. На рисунке 3.14 представлен фрагмент интерфейса программы Neural Analizer, с помощью которой производилось прогнозирование температуры.


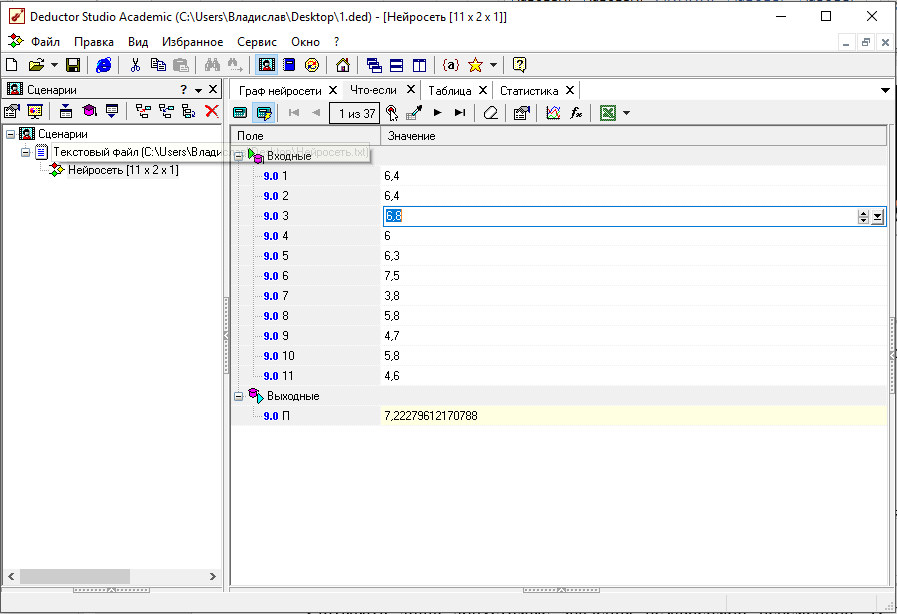
    Рис. 3.14. Прогнозирование температуры с помощью искусственной нейросети
    Полученные с помощью искусственной нейронной сети результаты сравнивались с фактическими значениями. По результатам сравнения была рассчитана средняя абсолютная ошибка прогноза, которая оказалась равна 0,25°С.

    Таким образом, можно сделать следующие выводы.

    1. Существует возможность прогнозирования среднегодовой температуры воздуха на основе данных за предшествующие годы.

    2. Сравнение точности различных методов прогнозирование позволяет рекомендовать использовать в прогностических целях полином третьей степени.

    3. Точность разработанных прогнозов (0,2 °С) можно признать удовлетворительной.
    1   2   3   4   5   6   7   8   9   10   11

    написать администратору сайта