Методика расчета кинематических характеристик ЭОШ ПУС РДТТ на ос. Методика расчета кинематических характеристик эластичноопорного шарнира поворотного сопла ракетных двигателей твердого топлива
 Скачать 150.71 Kb. Скачать 150.71 Kb.
|
|
Методика расчета кинематических характеристик эластично-опорного шарнира поворотного сопла ракетных двигателей твердого топлива ©  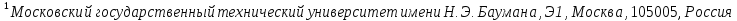 Аннотация: Особо актуальной задачей является изменение вектора скорости летательного аппарата в полете. Наиболее перспективным решением является создание методов теоретического проектирования поворотно управляющих сопел, тип уплотнения и выбор рулевой машинки которых характеризует эффективность движителя. С точки зрения требований, предъявляемых к современным двигателям твердого топлива, наиболее предпочтительная система управления включает в себя гидравлическую рулевую машинку и тип уплотнения эластично-опорного шарнира. В данной работе представлена методика расчета кинематики поворотно управляющего сопла ракетного двигателя твердого топлива на эластичном опорном шарнире с гидравлической рулевой машинкой. Ключевые слова: Поворотно управляющее сопло, эластично-опорный шарнир, шарнирный момент, позиционный момент, рулевая машинка, гидроцилиндр. Для управления движения летательного аппарата (ЛА) в соответствии с требуемой траекторией необходимо иметь возможность изменять в полете величину и направление вектора скорости, а также ориентацию осей ЛА в пространстве. С этой целью используются реактивные двигатели и различные органы управления, действие которых создает необходимые для управления силы и моменты. Приводы исполнительных органов управления могут быть гидравлическими, пневматическими, газовыми или электрическими. Использование поворотных сопел для управления (ПУС) вектором тяги является наиболее энергетически экономичным, т.к. управляющее усилие создается в результате осесимметричного и практически равномерного истечения продуктов сгорания и одновременного поворота докритической и закритической части сопла[1]. Достоинства управляющих сопел[2]:
Основными недостатками являются:
Эффективность поворотных управляющих сопел используемых в РДТТ во многом определяется типом уплотнения[3]. С точки зрения требований, предъявляемых к современным ракетным двигателям твердого топлива (РДТТ), наиболее предпочтительным типом уплотнения является эластичный опорный шарнир (ЭОШ) (рис.1). Он обладает наименьшим весом, относительной простотой в изготовлении и нашел наибольшее применение в существующих отечественных и зарубежных РДТТ. При отклонении подвижной части сопла в элементах ЭОШ возникает момент сопротивления повороту органа управления (ОУ) – шарнирный момент 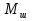 . Поэтому при проектировании ПУС чрезвычайно важно правильно спрогнозировать величины момента сопротивления и влияние составляющих на рабочие параметры РДТТ[1]. . Поэтому при проектировании ПУС чрезвычайно важно правильно спрогнозировать величины момента сопротивления и влияние составляющих на рабочие параметры РДТТ[1]. 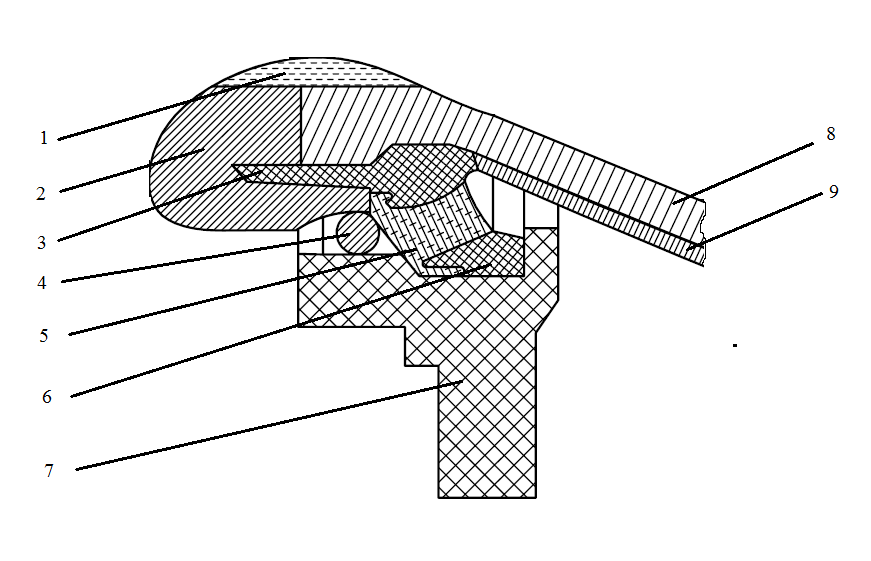 Рис.1 Поворотное сопло на эластичном опорном шарнире: 1-пирографит; 2- УУКН; 3,6 – опорные кольца; 4- спиральная намотка теплостойкого материала; 5- ЭОШ; 7- неподвижная часть сопла; 8- стеклопластик; 9- сталь 30 ХГСА Шарнирный момент 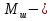 наибольший суммарный момент сопротивления повороту органа рулевого управления (ОУ) с заданными угловой скоростью наибольший суммарный момент сопротивления повороту органа рулевого управления (ОУ) с заданными угловой скоростью 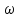 , угловым ускорением , угловым ускорением 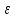 и углом поворота и углом поворота 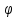 . Аналитическая зависимость шарнирного момента определяется следующей формулой[1]: . Аналитическая зависимость шарнирного момента определяется следующей формулой[1]: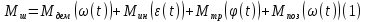 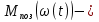 позиционный момент, пропорциональный углу поворота; позиционный момент, пропорциональный углу поворота;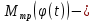 суммарный момент трения во всех соединениях ОУ; суммарный момент трения во всех соединениях ОУ;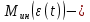 момент инерционных сил подвижных частей ОУ; момент инерционных сил подвижных частей ОУ;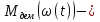 момент демпфирования газовой струи при отклонении ее с угловой скоростью момент демпфирования газовой струи при отклонении ее с угловой скоростью 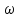 . .Позиционный момент является основной составляющей суммарного шарнирного момента ПУС РДТТ. С учетом геометрии, параметров работы ПУС, выражение (1) представляется в виде[1]: 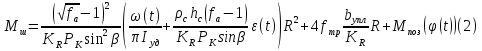 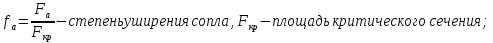 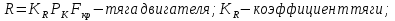 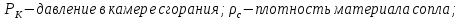 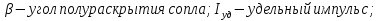 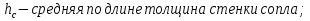  Позиционный момент приближенно определяется следующим образом: 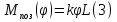 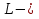 плечо, равное расстоянию от точки крепления РМ до центра поворота подвижной части ПУС, плечо, равное расстоянию от точки крепления РМ до центра поворота подвижной части ПУС, 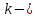 жесткость ЭОШ. жесткость ЭОШ.Требования, предъявляемые к органам управления[4,5]:
Этим требованиям наиболее полно удовлетворяют гидравлические приводы[1]. Методика расчета позволяет оценить необходимые параметры ПУС, а также исследовать кинематические характеристики ПУС РДТТ. В качестве ОУ применяется рулевая машинка(РМ), обеспечивающая поворот сопла на заданный угол 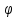 . Механизм РМ состоит из гидравлического цилиндра с поршнем . Механизм РМ состоит из гидравлического цилиндра с поршнем 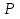 , шток которого шарнирно соединен с подвижной камерой сопла. Поворот осуществляется подачей рабочей жидкости от гидронасоса в полость гидроцилиндра. Регулировка подачи осуществляется различными технологиями. , шток которого шарнирно соединен с подвижной камерой сопла. Поворот осуществляется подачей рабочей жидкости от гидронасоса в полость гидроцилиндра. Регулировка подачи осуществляется различными технологиями.Задаваясь физико-инерционными параметрами ПУС РДТТ (материал составляющих, масса), необходимыми рабочими (тяга, давление в камере), а также масштабными и геометрическими, расчет кинематических характеристик основан на методе исследования динамики одномассовой динамической модели, вводя два фундаментальных варьируемых значения – угла поворота 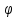 и времени поворота и времени поворота 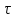 . Время поворота характеризует быстродействие изменение вектора скорости, обычно оно не превышает . Время поворота характеризует быстродействие изменение вектора скорости, обычно оно не превышает 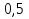 секунды. секунды. Методы исследования кинематики и динамики одномассовой динамической модели подразумевают расчет передаточных функций, инерционных составляющих согласно общей теории механизмов и машин[6], принимая за обобщенную координату – угол поворота 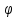 , а звено приведения – подвижную часть сопла ПУС РДТТ, при этом геометрически обеспечивая нулевой угол давления в начале движения(рис.2). , а звено приведения – подвижную часть сопла ПУС РДТТ, при этом геометрически обеспечивая нулевой угол давления в начале движения(рис.2). 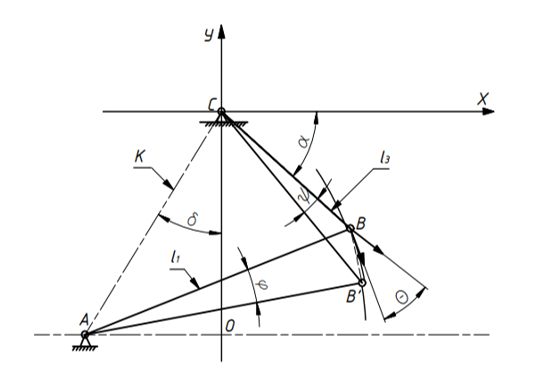 Рис.2. Расчетно-пояснительная схема кинематики ПУС РДТТ: А – центр поворота сопла, С – верхнее положение штока рулевой машинки, СВ, CB' – начальное и конечное положение гидроцилиндра соответственно, 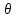 – угол давления, – угол давления, 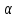 – начальный угол положения гидроцилиндра, – начальный угол положения гидроцилиндра, 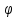 – угол поворота. – угол поворота.Расчет закона движения подвижной части ПУС РДТТ определяется интегрированием уравнения движения динамической модели в дифференциальной форме[6]: 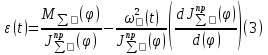 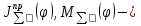 суммарный приведенный момент инерции и суммарный приведенный момент инерции и 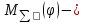 суммарный приведенный момент сил одномассовой динамической модели соответственно. суммарный приведенный момент сил одномассовой динамической модели соответственно.Cуммарный приведенный момент 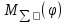 одномассовой динамической модели в уравнении (3) является функцией разности движущего момента, зависящего от давления в гидроцилиндре, и шарнирного момента. Уравнение момента сопротивления (2) включает в себя заданные законы угловой скорости одномассовой динамической модели в уравнении (3) является функцией разности движущего момента, зависящего от давления в гидроцилиндре, и шарнирного момента. Уравнение момента сопротивления (2) включает в себя заданные законы угловой скорости 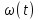 и углового ускорения и углового ускорения 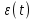 и их зависимости от обобщенной координаты изначально неизвестны. Поэтому стандартный подход к задаче определения закона движения существенно усложняется в отсутствии связи времени поворота и их зависимости от обобщенной координаты изначально неизвестны. Поэтому стандартный подход к задаче определения закона движения существенно усложняется в отсутствии связи времени поворота 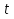 и угла поворота и угла поворота 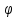 . Для определения закона движения, то есть функций . Для определения закона движения, то есть функций 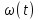 , , 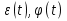 используются математические методы. Задана аналитическая функция, описывающая изменение теоретической угловой скорости используются математические методы. Задана аналитическая функция, описывающая изменение теоретической угловой скорости 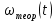 в заданном диапазоне времени для безударного режима пуск-останов: в заданном диапазоне времени для безударного режима пуск-останов: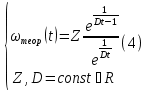 Промежуток изменения поворота сопел 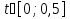 секунд. Константы подбираются из условия равенства площади подинтегральной функции секунд. Константы подбираются из условия равенства площади подинтегральной функции 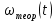 заданному углу поворта заданному углу поворта 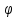 : :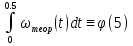 Зависимость углового ускорения от времени определяется аналитически: 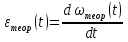 . Функцию вида (4) нельзя представить в виде сходящегося ряда, поэтому вид кривой зависимости . Функцию вида (4) нельзя представить в виде сходящегося ряда, поэтому вид кривой зависимости 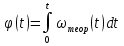 строится методом точечной аппроксимации или интегрируется графически на ЭВМ. Характерный вид кривых соответствует безударному режиму пуск-останов, который наиболее приемлемый для работы механизмов(Рис.3). строится методом точечной аппроксимации или интегрируется графически на ЭВМ. Характерный вид кривых соответствует безударному режиму пуск-останов, который наиболее приемлемый для работы механизмов(Рис.3).Рис.3. Характерный вид кривых функции (4) для 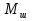 Пренебрегая силами тяжести гидроцилиндра, поршня и штока, по сравнению с усилиями тяги РДТТ и давления в гидроцилиндре, задаётся процентное соотношение разницы движущего момента- 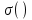 , определяемого параметром давления гидроцилиндре РМ, и момента сопротивления , определяемого параметром давления гидроцилиндре РМ, и момента сопротивления 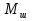 . . 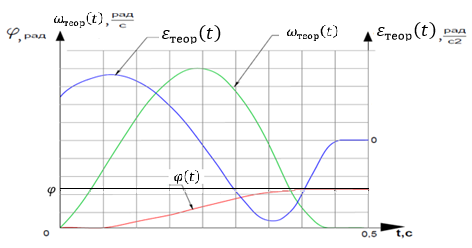 Рассчитывается давление в камере РМ: 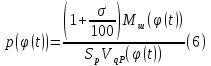 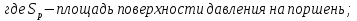 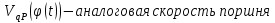 Суммарная работа движущего момента на звене приведения подвижной части сопла: 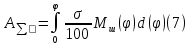 Согласно уравнению движения в форме энергий рассчитывается реальный закон изменения расчетной угловой скорости 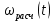 , учитывая инерционные составляющие частей ПУС РДТТ: , учитывая инерционные составляющие частей ПУС РДТТ: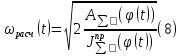 Расчетное угловое ускорение приведенного звена определяется уравнением движения динамической модели в дифференциальной форме: 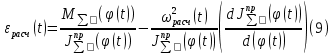 Интегрируя функцию угловой скорости, определяют зависимость времени от угла поворота, тем самым рассчитывая полностью закон движения ПУС РДДТ: 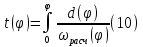 Заключение:
Список литературы:
|
