Статистика зачет. Контрольная по статистике. Методика выполнения самостоятельной работы (Вариант задания выбирается по двум последним цифрам зачетной книжки)
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
Контрольная работа Тема: Методика выполнения самостоятельной работы (Вариант задания выбирается по двум последним цифрам зачетной книжки) Цель работы: На основании экспериментальных данных определить оптимальную оценку математического ожидания, наиболее приближенную к истинной величине. Графически изобразить результаты анализа выборки. Проверить гипотезу о нормальном распределении. Программные продукты: Для выполнения работы использовать на выбор: OpenOffice Calc, Microsoft Excel или аналогичный программный продукт работающий с электронными таблицами. Отчет необходимо оформить в выбранном для расчета программном продукте или в Microsoft Word или OpenOffice Writer.  1. Упорядочить исходную выборку по возрастанию. 1.5 1.58 1.61 1.61 1.8 1.84 1.93 1.94 1.97 1.98 1.99 2.02 2.05 2.09 2.11 2.16 2.35 2.36 2.39 2.43 2.45 2.45 2.5 2.54 2.54 2.59 2.59 2.59 2.62 2.63 2.64 2.65 2.69 2.74 2.74 2.78 2.82 2.83 2.84 2.86 2.88 2.89 2.93 2. Вычислить средние значения, указанные в вашем варианте заданий. Вычислить дисперсии, квадратичные отклонения и сделать вывод об эффективности оценок на их основании. - Арифметическое среднее: 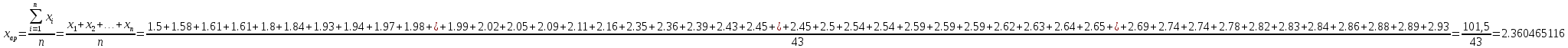 - Гармоническое среднее:  - Кубическое среднее: 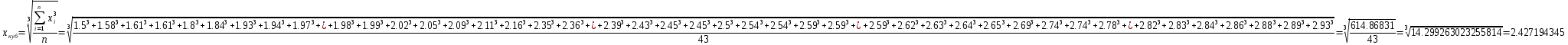 - Дисперсия для арифметического среднего: 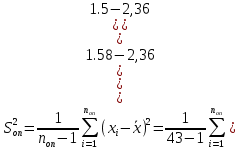 - Дисперсия для гармонического среднего: 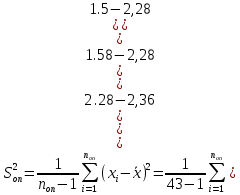 - Дисперсия для кубического среднего: 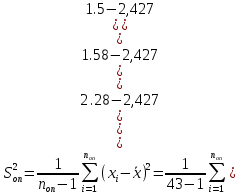 - Квадратичное отклонение для арифметического среднего 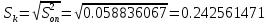 - Квадратичное отклонение для гармонического среднего 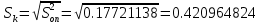 - Квадратичное отклонение для кубического среднего 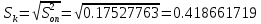 Р 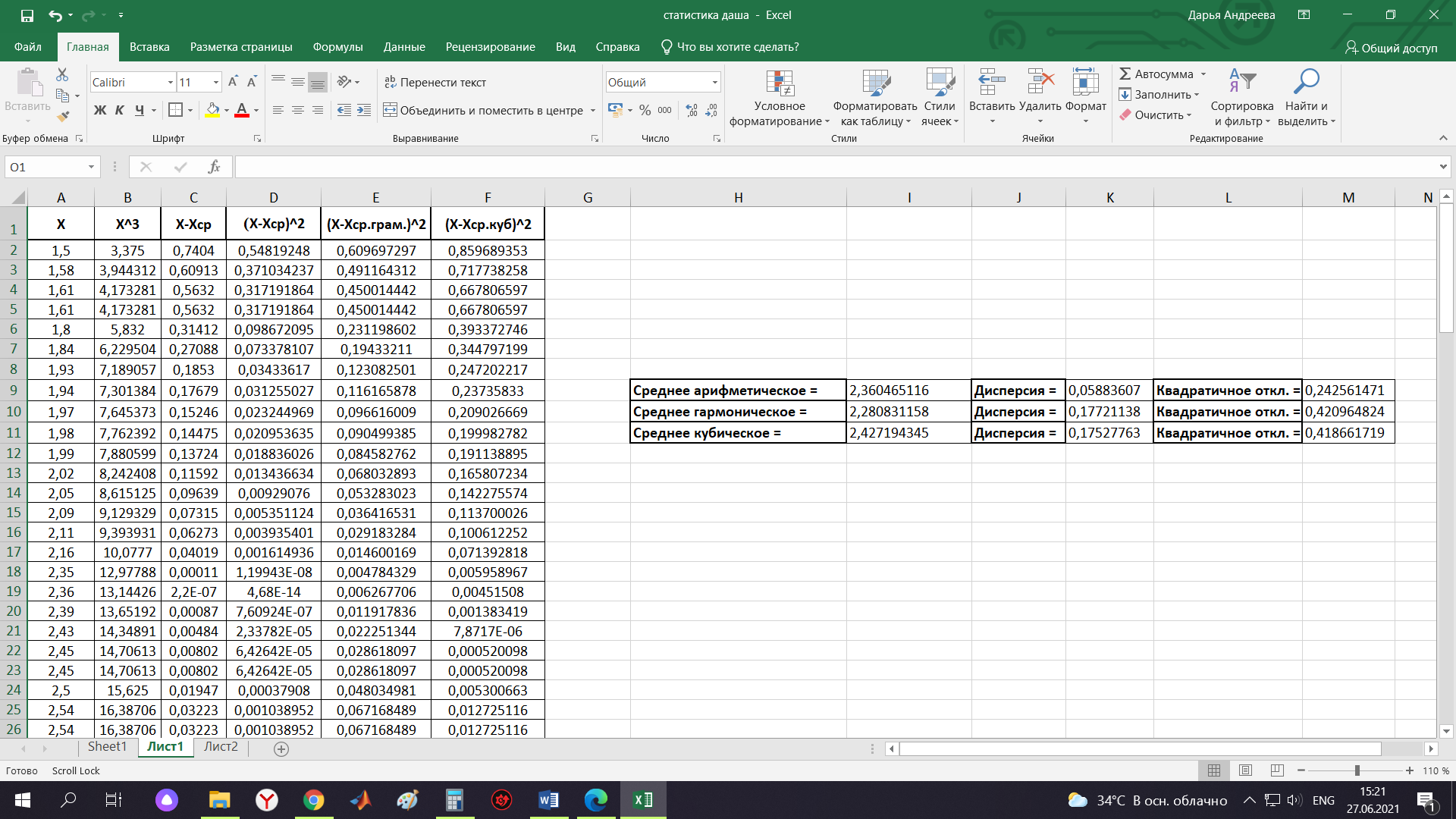 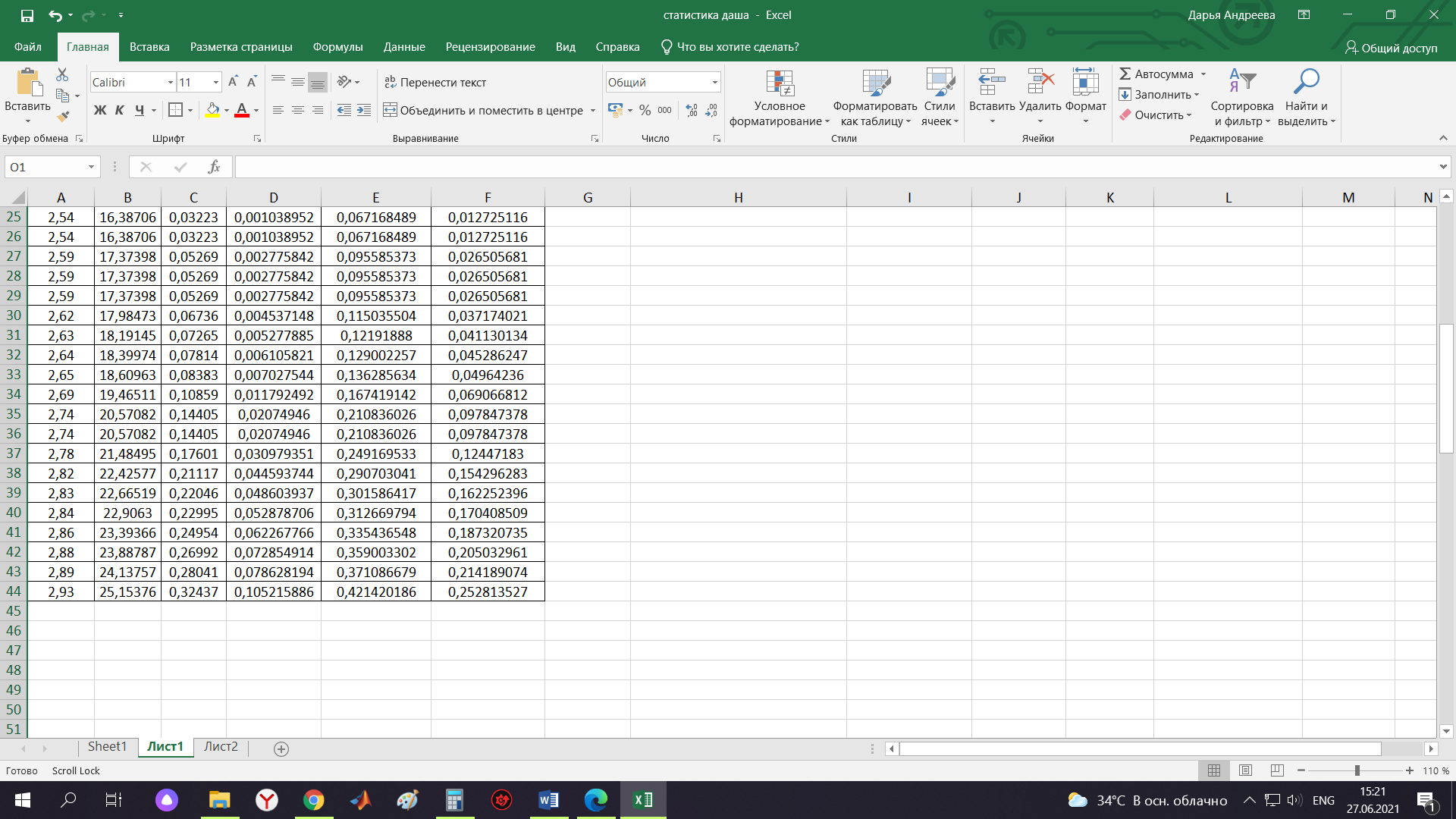 асчеты в программе MicrosoftExcel Вывод: у арифметического среднего минимальная дисперсия S2on = 0,00074417. Отсюда следует, что арифметическое среднее является эффективной статистической оценкой. 3. Вычислить коэффициент вариации, указать относительную погрешность эксперимента. Построить доверительный интервал по правилу, указанному в вашем варианте. На основании построенного интервала указать точки, подлежащие отсеву. 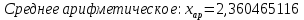 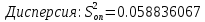 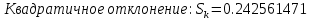 Коэффициент вариации: 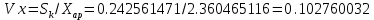 Относительная погрешность эксперимента = 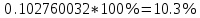 Расчеты в программе MicrosoftExcel 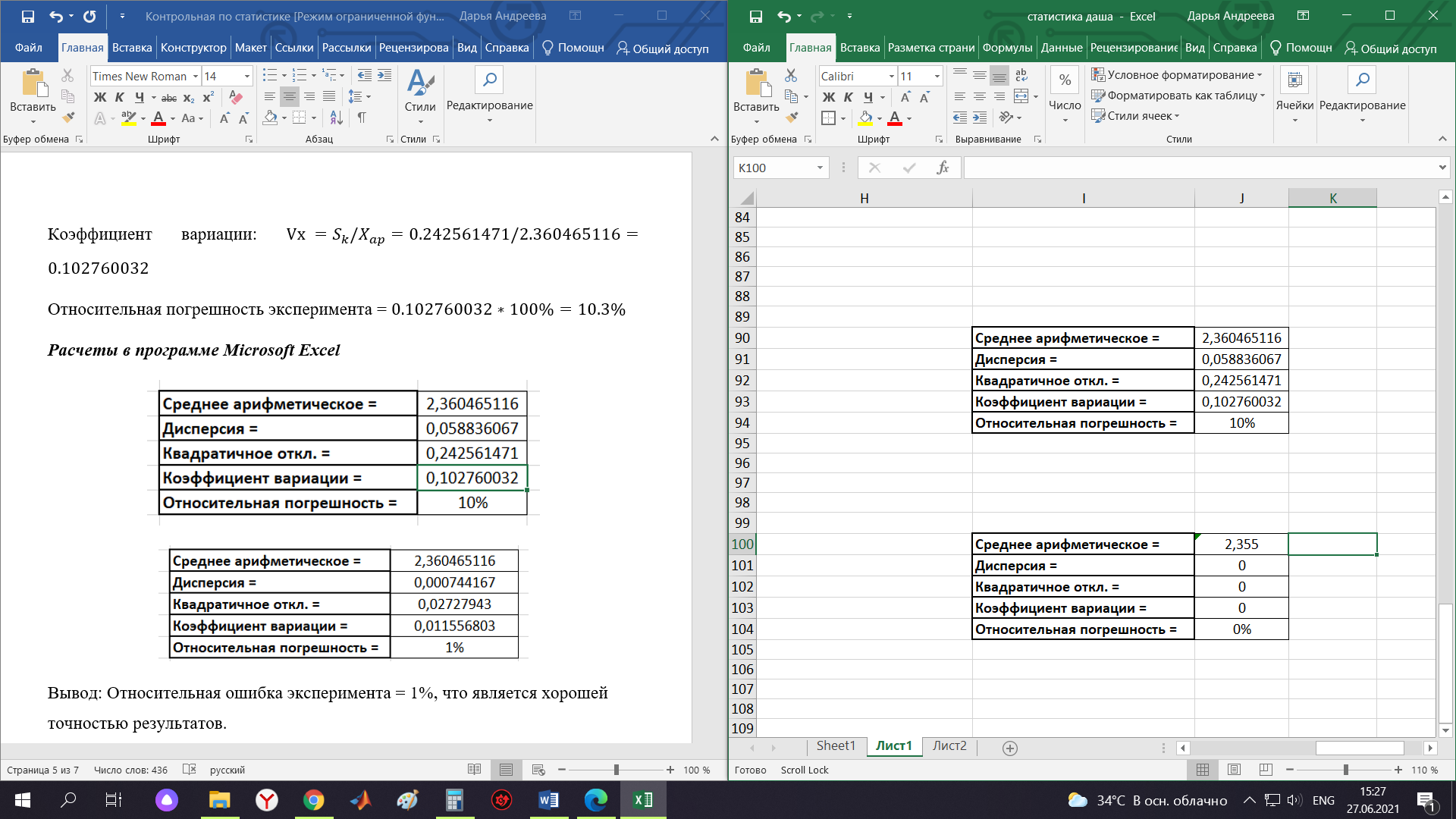 Вывод: Относительная ошибка эксперимента = 10%, что является хорошей точностью результатов. Математическое ожидание коэффициента 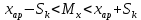 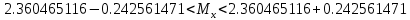 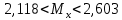 Укажем доверительное отклонение: 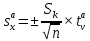 v = n-1=43-1=42 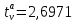 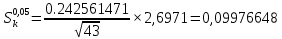 Построение доверительного интервала 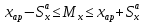 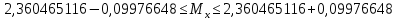 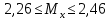 Уровень значимости α=0.01 Найдем «выпадающие точки»: Выпадающими точками являются следующие 37 значений: 1,5 1,58 1,61 1,61 1,8 1,84 1,93 1,94 1,97 1,98 1,99 2,02 2,05 2,09 2,11 2,16 2,5 2,54 2,54 2,59 2,59 2,59 2,62 2,63 2,64 2,65 2,74 2,74 2,78 2,82 2,83 2,84 2,86 2,88 2,89 2,93 Оставшиеся 6 значений: 2,35 2,36 2,39 2,43 2,45 2,45 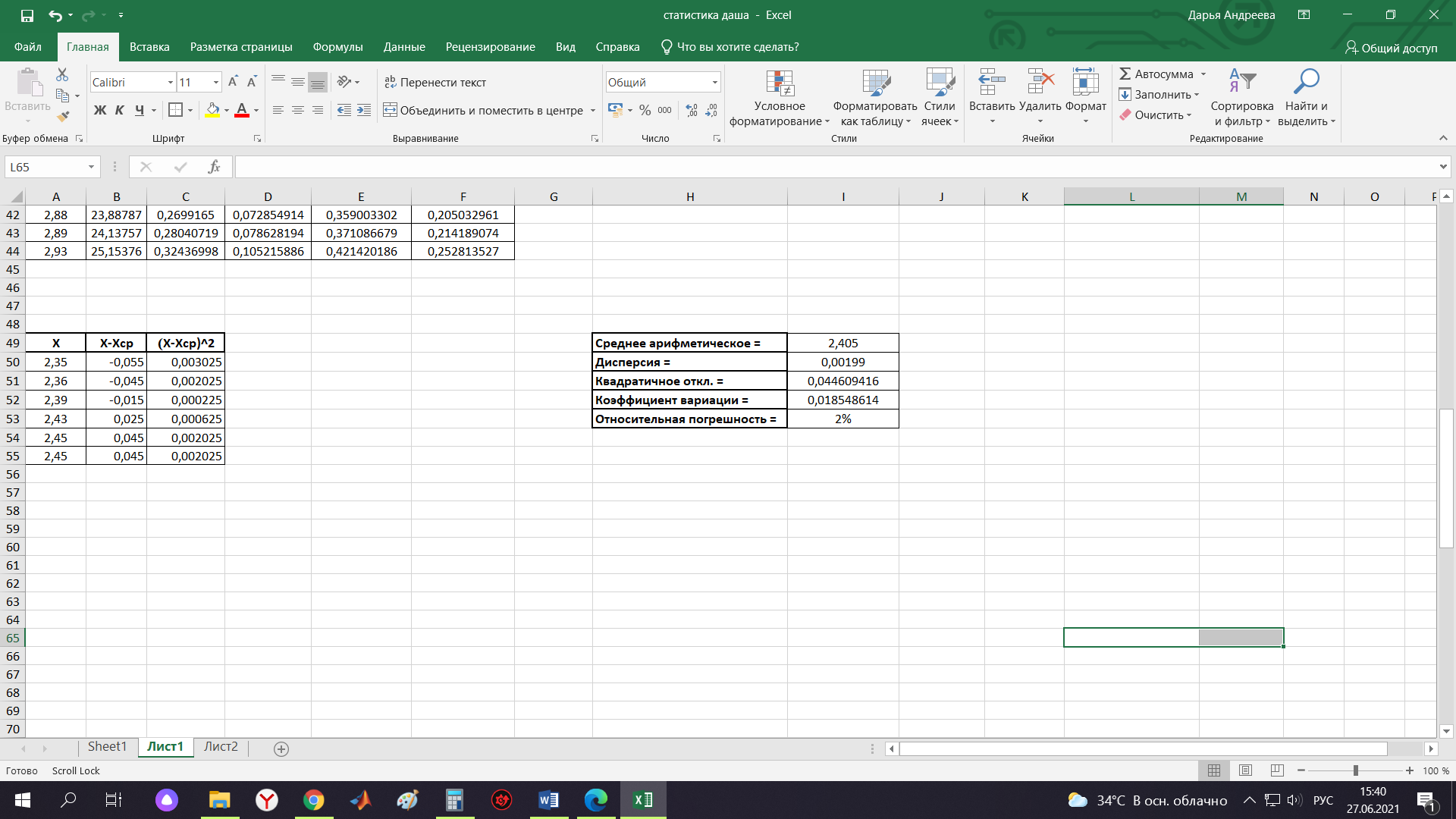 Вывод: относительная ошибка эксперимента снизилась с 10% до 2%. Этот факт демонстрирует целесообразность применения процедуры отсева выпадающих точек, для получения более точного результата оценки статистических характеристик. 4. По исходной выборке построить интервальный вариационный ряд, взять количество интервалов k n. И 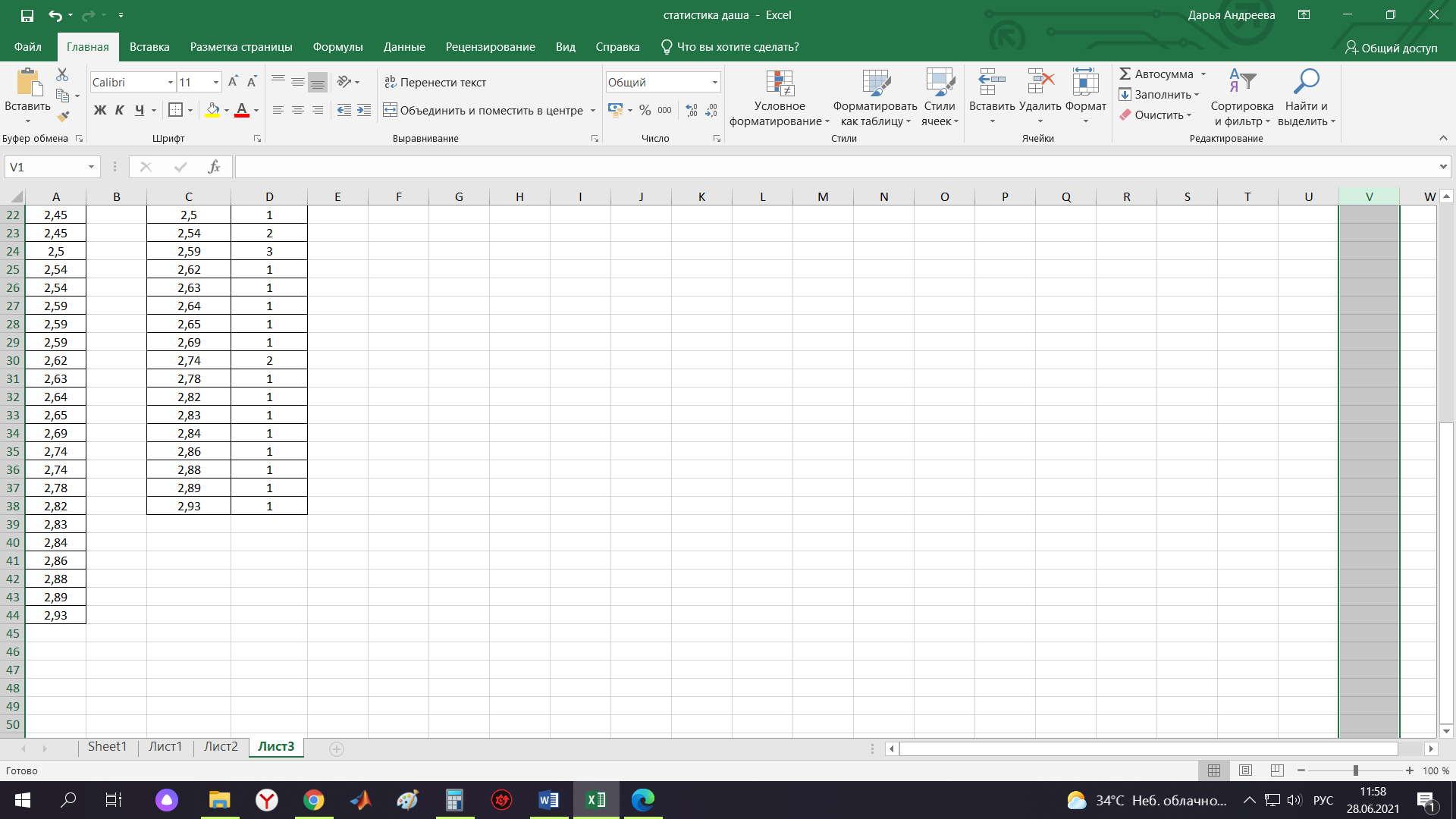 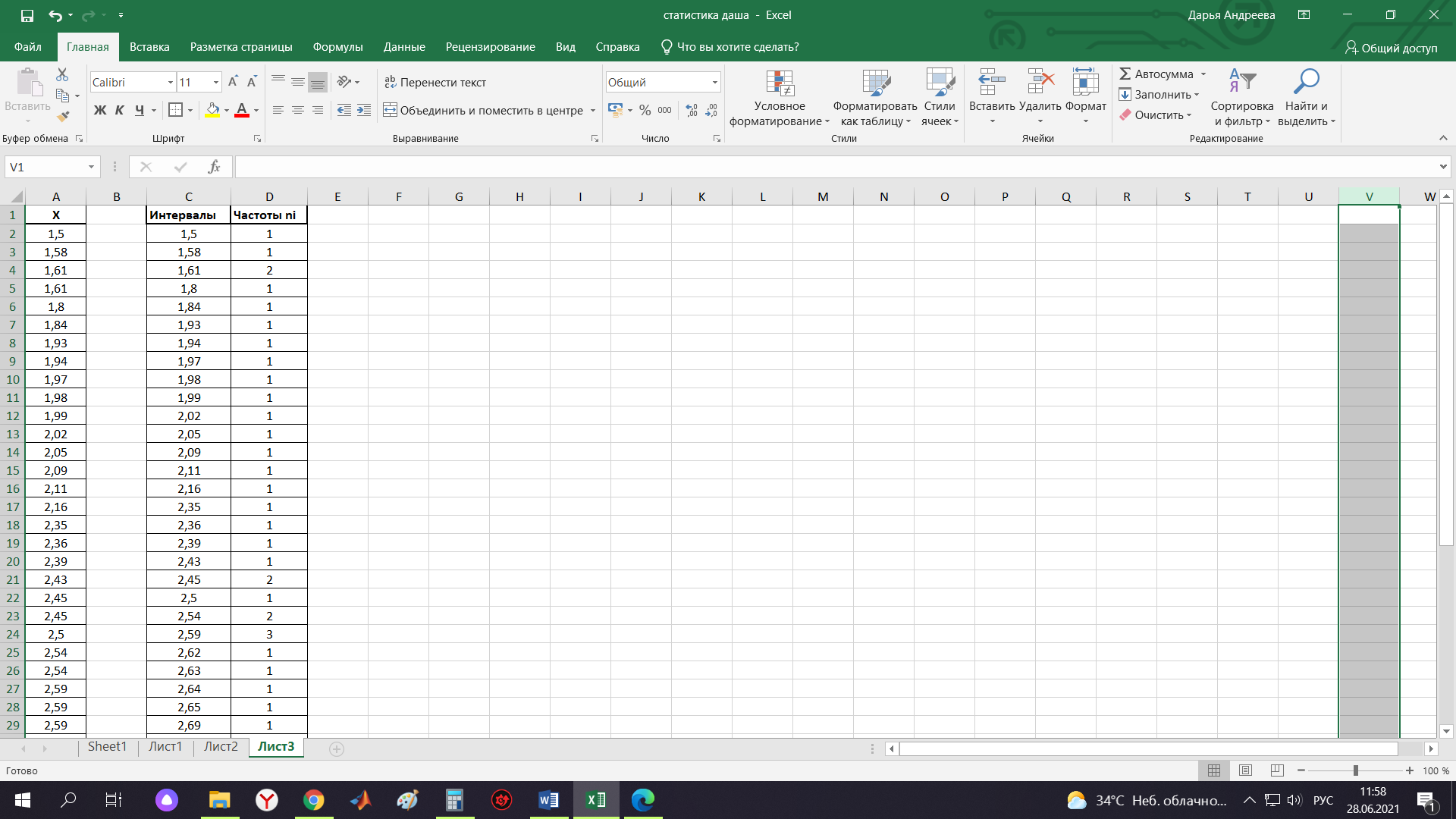 нтервальный вариационный ряд Вывод: в результате расчетов мы получили, что K=37 ≈ n=43. 5. Согласно вашему варианту построить графические представления интервального вариационного ряда. 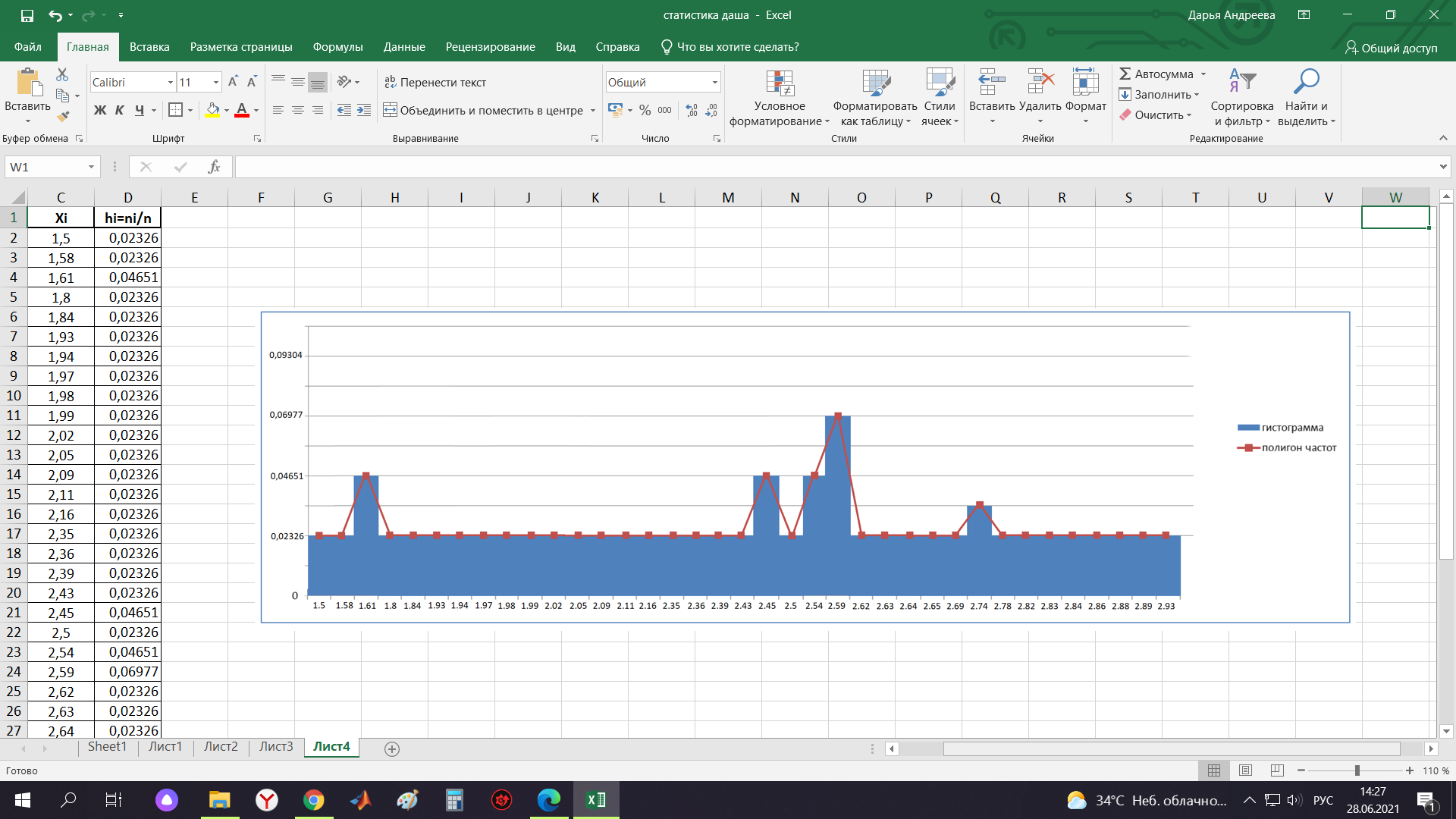  |
