Метрика Холстеда
 Скачать 98.16 Kb. Скачать 98.16 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА №1 по дисциплине: Метрология и квалиметрия программного обеспечения тема: «Метрика Холстеда» ОГЛАВЛЕНИ ЦЕЛЬ РАБОТЫ И ЗАДАНИЕ 2 1МЕТРИКА ХОЛСТЕДА ДЛЯ ОЦЕНКИ СЛОЖНОСТИ ПРОГРАММ 3 2ПРОЦЕСС РАСЧЁТА МЕТРИКИ 4 3АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ 8 ЗАКЛЮЧЕНИЕ 10 ЦЕЛЬ РАБОТЫ И ЗАДАНИЕ 3 1 МЕТРИКА ХОЛСТЕДА ДЛЯ ОЦЕНКИ СЛОЖНОСТИ ПРОГРАММ 4 2 ПРОЦЕСС РАСЧЁТА МЕТРИКИ 5 3 АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ 9 ЗАКЛЮЧЕНИЕ 11 СПИСОК ЛИТЕРАТУРЫ 12 ЦЕЛЬ РАБОТЫ И ЗАДАНИЕЦелью работы является изучение метрики Холстеда для оценки сложности размера кодов трех компьютерных программ. Результатом лабораторной работы № 1 является отчёт, в котором должны быть приведена метрика Холстеда в табличном виде для трех видов программ. Для выполнения лабораторной работы № 1 студент должен изучить приведённый ниже теоретический материал на тему «Метрика Холстеда». Для вычисления параметров метрики Холстеда необходимо подсчитать число используемых в программе операторов и операндов (общее число и число различных). Далее в соответствии с формулами из теоретического материала рассчитать все метрические параметры. Отчёт сдаётся в электронном (файл Word) виде. МЕТРИКА ХОЛСТЕДА ДЛЯ ОЦЕНКИ СЛОЖНОСТИ ПРОГРАММПри оценке сложности программ, как правило, выделяют три основные группы метрик: метрики размера программ, метрики сложности потока управления программ и метрики сложности потока данных программ. Оценки первой группы наиболее просты и поэтому получили широкое распространение. Основу метрики Холстеда составляют четыре измеряемые характеристики программы: 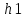 – число уникальных операторов программы, включая символы-разделители, имена процедур и знаки операций (словарь операторов); – число уникальных операторов программы, включая символы-разделители, имена процедур и знаки операций (словарь операторов); 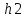 – число уникальных операндов программы (словарь операндов); – число уникальных операндов программы (словарь операндов); 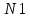 – общее число операторов в программе – общее число операторов в программе 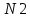 – общее число операндов в программе. – общее число операндов в программе.Опираясь на эти характеристики, получаемые непосредственно при анализе исходных текстов программ, Холстед вводит следующие оценки: 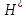 — теоретический словарь программы, — теоретический словарь программы,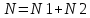 — длина программы, — длина программы,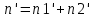 — теоретический словарь программы, — теоретический словарь программы,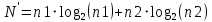 — теоретическая длина программы, — теоретическая длина программы,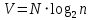 — объем программы, — объем программы,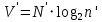 — потенциальный объем программы, — потенциальный объем программы,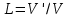 — уровень качества программирования, — уровень качества программирования,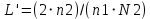 — уровень качества программирования, — уровень качества программирования,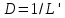 — средний коэффициент сложности, — средний коэффициент сложности,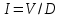 — информационное содержание программы, — информационное содержание программы,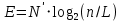 — оценка необходимых интеллектуальных усилий при разработке программы, характеризующая число требуемых элементарных решений при написании программы. — оценка необходимых интеллектуальных усилий при разработке программы, характеризующая число требуемых элементарных решений при написании программы.При применении метрик Холстеда частично компенсируются недостатки, связанные с возможностью записи одной и той же функциональности разным количеством строк и операторов. ПРОЦЕСС РАСЧЁТА МЕТРИКИПрограмма 1. Найти наименьшее число, большее заданного N, такое, что сумма квадратов его десятичных цифр есть полный квадрат (например, таким является число 442: 42+42+22=36=62). Листинг 1
Проведём подсчёт операторов и операндов программы 1. Таблица 1 – Операторы и операнды программы 1
Программа 2. Найти в заданном диапазоне от N1 до N2 (N2>N1) два простых числа, имеющие минимальное и максимальное значения произведений начала и конца своего десятичного представления. Листинг 2
Проведём подсчёт операторов и операндов программы 2. Таблица 2 – Операторы и операнды программы 2
Программа 3. Найти первые N последовательно возрастающих на величину k чисел, меньших заданного числа, все нетривиальные делители которых различны (два таких числа, возрастающих на 1 – это 14=2*7 и 15=3*5). Листинг 3
Проведём подсчёт операторов и операндов программы 3. Таблица 3 – Операторы и операнды программы 3
Окончание таблицы 3
АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВПроанализируем полученные результаты в таблицах 1-3 и проведём расчёт характеристик метрики Холстеда для всех программ. Результаты отобразим в таблице 4. Таблица 4 – Сводная таблица характеристик метрики Холстеда
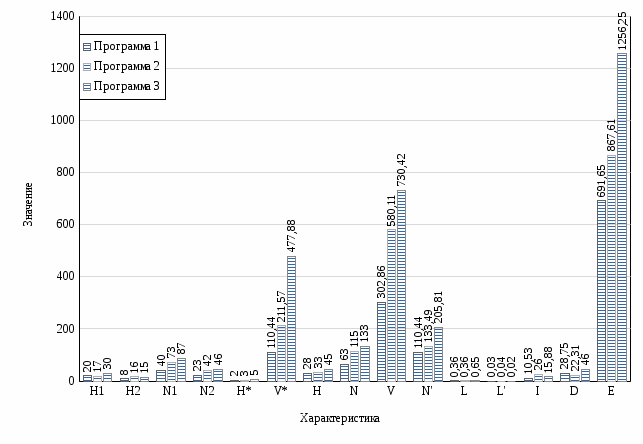 Рисунок 1 – Сравнение характеристик метрики Холстеда между 3 программами Программы имеют приблизительно одинаковое количество уникальных операндов и операторов, однако при этом имеют различную сложность. Уровень качества программирования всех программ меньше единицы, содержательная нагрузка на каждый компонент программы небольшая, так как все три функции полностью реализуют уникальную логику. Интеллектуально содержание алгоритмов также примерно одинаково, только у программы 2 оно выше почти в 2 раза. Если сравнивать количество мысленных элементарных решений, принимаемых в процессе написания программ, то заметен рост этого показателя с усложнением исходной задачи алгоритма. ЗАКЛЮЧЕНИЕВ результате выполненной работы были получены навыки использования метрики Холстеда с целью оценки сложности размера кода программ. В ходе работы была произведена оценка (было подсчитано число используемых в программе операторов и операндов для последующего расчёта по приведённым формулам) трёх компьютерных программ, результаты которой были приведены в табличном виде и в виде графика. Метод Холстеда хоть и позволяет выделить определённые закономерности и оценить эффективность программы, однако, на практике необходимо более комплексное исследование, которое не ограничивается лишь одним методом. Новосибирск 2022 г. |
