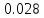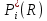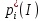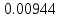РГЗ метрология. Метрология, стандартизация и сертификация
 Скачать 86.43 Kb. Скачать 86.43 Kb.
|
|
Расчетно-графическое задание по дисциплине “Метрология, стандартизация и сертификация” ВведениеЦели работы: 1. Закрепление теоретических знаний, полученных на лекциях; 2. Умение применять теоретические знания на практике; 3. Закрепление навыков расчёта результатов прямых измерений и исключение грубых ошибок; 4. Закрепление навыка оценки погрешностей косвенных измерений с использованием результатов многократных прямых измерений. Исходные данные:  , ,   = {0.107487, 0.0912066, 0.106768, 0.0932926, 0.0922078, 0.0941802, 0.104049, 0.0971135, 0.0813934, 0.0982629, 0.0918624, 0.0972559, 0.101069, 0.0968043, 0.0909243, 0.124971, 0.09736, 0.102644, 0.103404, 0.0814226, 0.955689, 0.0852121, 0.0873002, 0.0891231, 0.10806, 0.101913, 0.102692, 0.114892, 0.0863937, 0.0795341, 0.0937686, 0.102873, 0.0891076, 0.104804, 0.112248, 0.109677, 0.0978007, 0.0962719, 0.0967213, 0.109343, 0.106599, 0.0913581, 0.0903212, 0.101844, 0.0967749, 0.084631, 0.123045, 0.0799222, 0.118133, 0.104393}; = {0.107487, 0.0912066, 0.106768, 0.0932926, 0.0922078, 0.0941802, 0.104049, 0.0971135, 0.0813934, 0.0982629, 0.0918624, 0.0972559, 0.101069, 0.0968043, 0.0909243, 0.124971, 0.09736, 0.102644, 0.103404, 0.0814226, 0.955689, 0.0852121, 0.0873002, 0.0891231, 0.10806, 0.101913, 0.102692, 0.114892, 0.0863937, 0.0795341, 0.0937686, 0.102873, 0.0891076, 0.104804, 0.112248, 0.109677, 0.0978007, 0.0962719, 0.0967213, 0.109343, 0.106599, 0.0913581, 0.0903212, 0.101844, 0.0967749, 0.084631, 0.123045, 0.0799222, 0.118133, 0.104393};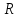 = {123.532, 117.013, 119.918, 118.837, 119.08, 122.052, 120.009, 116.409, 120.352, 113.861, 119.592, 120.425, 120.74, 114.393, 127.519, 122.052, 119.388, 121.444, 124.034, 118.657, 117.744, 119.637, 121.761, 116.673, 122.466, 120.265, 121.386, 122.368, 121.709, 121.458, 120.524, 116.341, 124.175, 124.944, 137.698, 122.394, 117.736, 119.174, 121.228, 117.315, 123.605, 123.441, 118.265, 119.823, 118.261, 119.352, 122.075, 120.798, 118.032, 117.203}; = {123.532, 117.013, 119.918, 118.837, 119.08, 122.052, 120.009, 116.409, 120.352, 113.861, 119.592, 120.425, 120.74, 114.393, 127.519, 122.052, 119.388, 121.444, 124.034, 118.657, 117.744, 119.637, 121.761, 116.673, 122.466, 120.265, 121.386, 122.368, 121.709, 121.458, 120.524, 116.341, 124.175, 124.944, 137.698, 122.394, 117.736, 119.174, 121.228, 117.315, 123.605, 123.441, 118.265, 119.823, 118.261, 119.352, 122.075, 120.798, 118.032, 117.203};1. Расчет результатов прямых измерений.1.1 Расчет среднеарифметического значения результатов наблюдений.Среднее арифметическое результатов измерений каждого из параметров есть величина (  ): ):  (1) (1)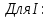 (0.107487 + 0.0912066 + 0.106768 + 0.0932926 + 0.0922078 + 0.0941802 + 0.104049 + 0.0971135 + 0.0813934 + 0.0982629 + 0.0918624 + 0.0972559 + 0.101069 + 0.0968043 + 0.0909243 + 0.124971 + 0.09736 + 0.102644 + 0.103404 + 0.0814226 + 0.955689 + 0.0852121 + 0.0873002 + 0.0891231 + 0.10806 + 0.101913 + 0.102692 + 0.114892 + 0.0863937 + 0.0795341 + 0.0937686 + 0.102873 + 0.0891076 + 0.104804 + 0.112248 + 0.109677 + 0.0978007 + 0.0962719 + 0.0967213 + 0.109343 + 0.106599 + 0.0913581 + 0.0903212 + 0.101844 + 0.0967749 + 0.084631 + 0.123045 + 0.0799222 + 0.118133 + 0.104393)/50 = 0.1155 А. (0.107487 + 0.0912066 + 0.106768 + 0.0932926 + 0.0922078 + 0.0941802 + 0.104049 + 0.0971135 + 0.0813934 + 0.0982629 + 0.0918624 + 0.0972559 + 0.101069 + 0.0968043 + 0.0909243 + 0.124971 + 0.09736 + 0.102644 + 0.103404 + 0.0814226 + 0.955689 + 0.0852121 + 0.0873002 + 0.0891231 + 0.10806 + 0.101913 + 0.102692 + 0.114892 + 0.0863937 + 0.0795341 + 0.0937686 + 0.102873 + 0.0891076 + 0.104804 + 0.112248 + 0.109677 + 0.0978007 + 0.0962719 + 0.0967213 + 0.109343 + 0.106599 + 0.0913581 + 0.0903212 + 0.101844 + 0.0967749 + 0.084631 + 0.123045 + 0.0799222 + 0.118133 + 0.104393)/50 = 0.1155 А.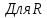 : (123.532+ 117.013+ 119.918+118.837+ 119.08+ 122.052+ 120.009+ 116.409+ 120.352+ 113.861+ 119.592+ 120.425+ 120.74+ 114.393+ 127.519+ 122.052+ 119.388+ 121.444+ 124.034+ 118.657+ 117.744+ 119.637+ 121.761+ 116.673+ 122.466+ 120.265+ 121.386+ 122.368+ 121.709+ 121.458+ 120.524+ 116.341+ 124.175+ 124.944+ 137.698+ 122.394+ 117.736+ 119.174+ 121.228+ 117.315+ 123.605+ 123.441+ 118.265+ 119.823+ 118.261+ 119.352+ 122.075+ 120.798+ 118.032+ 117.203)/50=120.543 Ом. : (123.532+ 117.013+ 119.918+118.837+ 119.08+ 122.052+ 120.009+ 116.409+ 120.352+ 113.861+ 119.592+ 120.425+ 120.74+ 114.393+ 127.519+ 122.052+ 119.388+ 121.444+ 124.034+ 118.657+ 117.744+ 119.637+ 121.761+ 116.673+ 122.466+ 120.265+ 121.386+ 122.368+ 121.709+ 121.458+ 120.524+ 116.341+ 124.175+ 124.944+ 137.698+ 122.394+ 117.736+ 119.174+ 121.228+ 117.315+ 123.605+ 123.441+ 118.265+ 119.823+ 118.261+ 119.352+ 122.075+ 120.798+ 118.032+ 117.203)/50=120.543 Ом.где  - измеряемая величина, - измеряемая величина,  - результаты отдельных измерений, - результаты отдельных измерений,  - число отдельных измерений. - число отдельных измерений.Результаты измерений величин приводятся в таблице 1. Таблица 1 - Среднеарифметические значения
1.2 Расчет среднеквадратического отклонения результатов наблюдений. Оценка среднеквадратического отклонения результатов единичных измерений ( Оценка среднеквадратического отклонения результатов единичных измерений ( ): ): 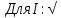 (((0.107487 + (-0.1155) + 0.0912066 + (-0.1155) + 0.106768 + (-0.1155) + 0.0932926 + (((0.107487 + (-0.1155) + 0.0912066 + (-0.1155) + 0.106768 + (-0.1155) + 0.0932926 + (-0.1155) + 0.0922078 + (-0.1155) + 0.0941802 + (-0.1155) + 0.104049 + (-0.1155) + 0.0971135 + (-0.1155) + 0.0813934 + (-0.1155) + 0.0982629 + (-0.1155) + 0.0918624 + (-0.1155) + 0.0972559 + (-0.1155) + 0.101069 + (-0.1155) + 0.0968043 + (-0.1155) + 0.0909243 + (-0.1155) + 0.124971 + (-0.1155) + 0.09736 + (-0.1155) + 0.102644 + (-0.1155) + 0.103404 + (-0.1155) + 0.0814226 + (-0.1155) + 0.955689 + (-0.1155) + 0.0852121 + (-0.1155) + 0.0873002 + (-0.1155) + 0.0891231 + (-0.1155) + 0.10806 + (-0.1155) + 0.101913 + (-0.1155) + 0.102692 + (-0.1155) + 0.114892 + (-0.1155) + 0.0863937 + (-0.1155) + 0.0795341 + (-0.1155) + 0.0937686 + (-0.1155) + 0.102873 + (-0.1155) + 0.0891076 + (-0.1155) + 0.104804 + (-0.1155) + 0.112248 + (-0.1155) + 0.109677 + (-0.1155) + 0.0978007 + (-0.1155) + 0.0962719 + (-0.1155) + 0.0967213 + (-0.1155) + 0.109343 + (-0.1155) + 0.106599 + (-0.1155) + 0.0913581 + (-0.1155) + 0.0903212 + (-0.1155) + 0.101844 + (-0.1155) + 0.0967749 + (-0.1155) + 0.084631 + (-0.1155) + 0.123045 + (-0.1155) + 0.0799222 + (-0.1155) + 0.118133 + (-0.1155) + 0.104393 + (-0.1155))^2)/49)= 0.1217 А. 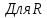 : : (((123.532 + (-120.543) + 117.013 + (-120.543) + 119.918 + (-120.543) + 118.837 + (((123.532 + (-120.543) + 117.013 + (-120.543) + 119.918 + (-120.543) + 118.837 + (-120.543) + 119.08 + (-120.543) + 122.052 + (-120.543) + 120.009 + (-120.543) + 116.409 + (-120.543) + 120.352 + (-120.543) + 113.861 + (-120.543) + 119.592 + (-120.543) + 120.425 + (-120.543) + 120.74 + (-120.543) + 114.393 + (-120.543) + 127.519 + (-120.543) + 122.052 + (-120.543) + 119.388 + (-120.543) + 121.444 + (-120.543) + 124.034 + (-120.543) + 118.657 + (-120.543) + 117.744 + (-120.543) + 119.637 + (-120.543) + 121.761 + (-120.543) + 116.673 + (-120.543) + 122.466 + (-120.543) + 120.265 + (-120.543) + 121.386 + (-120.543) + 122.368 + (-120.543) + 121.709 + (-120.543) + 121.458 + (-120.543) + 120.524 + (-120.543) + 116.341 + (-120.543) + 124.175 + (-120.543) + 124.944 + (-120.543) + 137.698 + (-120.543) + 122.394 + (-120.543) + 117.736 + (-120.543) + 119.174 + (-120.543) + 121.228 + (-120.543) + 117.315 + (-120.543) + 123.605 + (-120.543) + 123.441 + (-120.543) + 118.265 + (-120.543) + 119.823 + (-120.543) + 118.261 + (-120.543) + 119.352 + (-120.543) + 122.075 + (-120.543) + 120.798 + (-120.543) + 118.032 + (-120.543) + 117.203 + (-120.543))^2)/49)=3.6491 Ом. Для наблюдений значений среднеквадратические отклонения результатов приводятся в таблице 2. Таблица 2 - Среднеквадратические отклонения результатов наблюдения
1.3 Выявление грубых ошибок.Выявить и исключить грубые ошибки по критерию ±2σ и произвести расчет среднеквадратического значения и среднеквадратического отклонения без грубых ошибок. Таблица 3 – Значения грубых ошибок
Таблица 4 - Среднеарифметические значения без грубых ошибок
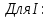 (0.107487 + 0.0912066 + 0.106768 + 0.0932926 + 0.0922078 + 0.0941802 + 0.104049 + 0.0971135 + 0.0813934 + 0.0982629 + 0.0918624 + 0.0972559 + 0.101069 + 0.0968043 + 0.0909243 + 0.09736 + 0.102644 + 0.103404 + 0.0814226 + 0.0852121 + 0.0873002 + 0.0891231 + 0.10806 + 0.101913 + 0.102692 + 0.114892 + 0.0863937 + 0.0795341 + 0.0937686 + 0.102873 + 0.0891076 + 0.104804 + 0.112248 + 0.109677 + 0.0978007 + 0.0962719 + 0.0967213 + 0.109343 + 0.106599 + 0.0913581 + 0.0903212 + 0.101844 + 0.0967749 + 0.084631 + 0.0799222 + 0.118133 + 0.104393)/47 = 0.0972 А. (0.107487 + 0.0912066 + 0.106768 + 0.0932926 + 0.0922078 + 0.0941802 + 0.104049 + 0.0971135 + 0.0813934 + 0.0982629 + 0.0918624 + 0.0972559 + 0.101069 + 0.0968043 + 0.0909243 + 0.09736 + 0.102644 + 0.103404 + 0.0814226 + 0.0852121 + 0.0873002 + 0.0891231 + 0.10806 + 0.101913 + 0.102692 + 0.114892 + 0.0863937 + 0.0795341 + 0.0937686 + 0.102873 + 0.0891076 + 0.104804 + 0.112248 + 0.109677 + 0.0978007 + 0.0962719 + 0.0967213 + 0.109343 + 0.106599 + 0.0913581 + 0.0903212 + 0.101844 + 0.0967749 + 0.084631 + 0.0799222 + 0.118133 + 0.104393)/47 = 0.0972 А.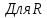 : (123.532+ 117.013+ 119.918+118.837+ 119.08+ 122.052+ 120.009+ 116.409+ 120.352 + 119.592+ 120.425+ 120.74 + 122.052+ 119.388+ 121.444+ 124.034+ 118.657+ 117.744+ 119.637+ 121.761+ 116.673+ 122.466+ 120.265+ 121.386+ 122.368+ 121.709+ 121.458+ 120.524+ 116.341+ 124.175+ 124.944+ 122.394+ 117.736+ 119.174+ 121.228+ 117.315+ 123.605+ 123.441+ 118.265+ 119.823+ 118.261+ 119.352+ 122.075+ 120.798+ 118.032+ 117.203)/46=120.3 Ом : (123.532+ 117.013+ 119.918+118.837+ 119.08+ 122.052+ 120.009+ 116.409+ 120.352 + 119.592+ 120.425+ 120.74 + 122.052+ 119.388+ 121.444+ 124.034+ 118.657+ 117.744+ 119.637+ 121.761+ 116.673+ 122.466+ 120.265+ 121.386+ 122.368+ 121.709+ 121.458+ 120.524+ 116.341+ 124.175+ 124.944+ 122.394+ 117.736+ 119.174+ 121.228+ 117.315+ 123.605+ 123.441+ 118.265+ 119.823+ 118.261+ 119.352+ 122.075+ 120.798+ 118.032+ 117.203)/46=120.3 ОмТаблица 5 - Среднеквадратические отклонения результатов наблюдения без грубых ошибок
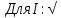 (((0.107487 + (-0.1155) + 0.0912066 + (-0.1155) + 0.106768 + (-0.1155) + 0.0932926 + (((0.107487 + (-0.1155) + 0.0912066 + (-0.1155) + 0.106768 + (-0.1155) + 0.0932926 + (-0.1155) + 0.0922078 + (-0.1155) + 0.0941802 + (-0.1155) + 0.104049 + (-0.1155) + 0.0971135 + (-0.1155) + 0.0813934 + (-0.1155) + 0.0982629 + (-0.1155) + 0.0918624 + (-0.1155) + 0.0972559 + (-0.1155) + 0.101069 + (-0.1155) + 0.0968043 + (-0.1155) + 0.0909243 + (-0.1155) + 0.09736 + (-0.1155) + 0.102644 + (-0.1155) + 0.103404 + (-0.1155) + 0.0814226 + (-0.1155) + 0.0852121 + (-0.1155) + 0.0873002 + (-0.1155) + 0.0891231 + (-0.1155) + 0.10806 + (-0.1155) + 0.101913 + (-0.1155) + 0.102692 + (-0.1155) + 0.114892 + (-0.1155) + 0.0863937 + (-0.1155) + 0.0795341 + (-0.1155) + 0.0937686 + (-0.1155) + 0.102873 + (-0.1155) + 0.0891076 + (-0.1155) + 0.104804 + (-0.1155) + 0.112248 + (-0.1155) + 0.109677 + (-0.1155) + 0.0978007 + (-0.1155) + 0.0962719 + (-0.1155) + 0.0967213 + (-0.1155) + 0.109343 + (-0.1155) + 0.106599 + (-0.1155) + 0.0913581 + (-0.1155) + 0.0903212 + (-0.1155) + 0.101844 + (-0.1155) + 0.0967749 + (-0.1155) + 0.084631 + (-0.1155) + 0.0799222 + (-0.1155) + 0.118133 + (-0.1155) + 0.104393 + (-0.1155))^2)/46)=0.094 А. 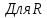 : : (((123.532 + (-120.543) + 117.013 + (-120.543) + 119.918 + (-120.543) + 118.837 + (((123.532 + (-120.543) + 117.013 + (-120.543) + 119.918 + (-120.543) + 118.837 + (-120.543) + 119.08 + (-120.543) + 122.052 + (-120.543) + 120.009 + (-120.543) + 116.409 + (-120.543) + 120.352 + (-120.543) + 119.592 + (-120.543) + 120.425 + (-120.543) + 120.74 + (-120.543) + 122.052 + (-120.543) + 119.388 + (-120.543) + 121.444 + (-120.543) + 124.034 + (-120.543) + 118.657 + (-120.543) + 117.744 + (-120.543) + 119.637 + (-120.543) + 121.761 + (-120.543) + 116.673 + (-120.543) + 122.466 + (-120.543) + 120.265 + (-120.543) + 121.386 + (-120.543) + 122.368 + (-120.543) + 121.709 + (-120.543) + 121.458 + (-120.543) + 120.524 + (-120.543) + 116.341 + (-120.543) + 124.175 + (-120.543) + 124.944 + (-120.543) + 122.394 + (-120.543) + 117.736 + (-120.543) + 119.174 + (-120.543) + 121.228 + (-120.543) + 117.315 + (-120.543) + 123.605 + (-120.543) + 123.441 + (-120.543) + 118.265 + (-120.543) + 119.823 + (-120.543) + 118.261 + (-120.543) + 119.352 + (-120.543) + 122.075 + (-120.543) + 120.798 + (-120.543) + 118.032 + (-120.543) + 117.203 + (-120.543))^2)/45)=2.2325Ом. 1.4 Оценка границ доверительного интервала Для оценки границ воспользуемся выражением  , (3) , (3)где 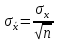 (4) (4)- среднеквадратическое отклонение среднего арифметического значения результатов измерений; 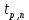 - коэффициент Стьюдента, выбранный в таблице величин коэффициента Стьюдента для различных значений доверительной вероятности. - коэффициент Стьюдента, выбранный в таблице величин коэффициента Стьюдента для различных значений доверительной вероятности.Из т. Стьюдента: t1 для 0.95 и 46 измерений = 2,01289, 𝑡2 для 47 измерений = 2,0117 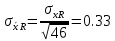 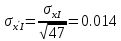 Найденные границы доверительных интервалов привести в таблице 6.   Таблица 6 – Границы доверительных интервалов для результатов прямых измерений
2. Построить гистограммы.1. Получаем результаты измерений x1,x2…xn Таблица 7 – Результаты измерений без промахов   2. Составим вариационные ряды результатов в порядке возрастания. Таблица 8 – Вариационные ряды в порядке возрастания   3. Разобьем на интервалы диапазон измерений. Ширина интервалов:  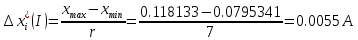 r=7 4. Определим границы интервалов. Границы интервалов: Для 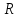 : :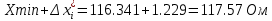 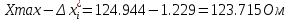 Для  : : А А А А5. Считаем частоты, равные числу результатов, лежащих в каждом i-м интервале 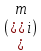 : :Таблица 9 – Количество измерений в заданных интервалах
6. Вычисляем вероятности попадания в i-ый интервал.  , n – общее число наблюдений. , n – общее число наблюдений.Таблица 10 – Вероятности попадания в заданные интервалы
7. Оценка средней плотности распределения в интервале.  Таблица 11 – Оценка средней плотности распределения
8. Отложим вдоль оси абсцисс интервалы в порядке возрастания индекса i и на каждом интервале построим прямоугольник высотой равной  . . 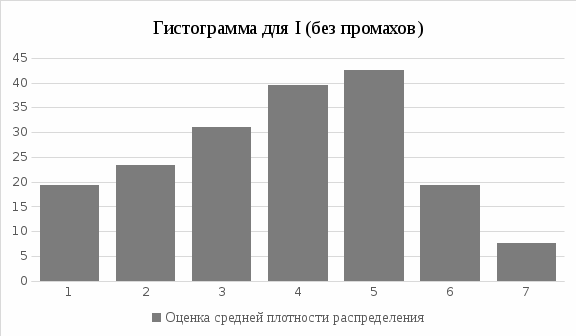 3. Расчет результатов косвенных измерений.3.1 Расчет среднего значения величины косвенного измерения. Значение величины косвенного измерения находится из средних арифметических значений результатов прямых измерений без грубых ошибок:  , , 3.2 Расчет коэффициентов влияния. Рассчитать абсолютные коэффициенты влияния согласно:  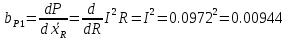  Коэффициенты влияния всегда рассчитываются именно для значений наблюдаемых величин. Найденные коэффициенты влияния занести в таблицу 12. Таблица 12 – Коэффициенты влияния для результатов прямых измерений
3.3 Расчет частных случайных погрешностей косвенного измерения. 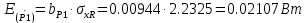  Таблица 13 – Частные случайные погрешности косвенного измерения
3.4 Расчет оценки среднего квадратического отклонения результата косвенного измерения ( 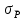 ). ). = = 3.5 Определение коэффициента Стьюдента для заданной доверительной вероятности и числа наблюдений. Значения t для доверительной вероятности 0,95: для 46, 47 измерений = 2,012 3.6 Расчет доверительной границы случайной погрешности результата косвенного измерения:  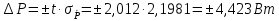 3.7 Определение результата косвенного измерения с указанием его погрешностей при Р = 0,95. Записать результат косвенного измерения  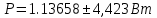 3.8 Анализ полученных результатов с использованием критерия ничтожных погрешностей. Если  , то погрешность считается ничтожной и может быть исключена из рассмотрения. , то погрешность считается ничтожной и может быть исключена из рассмотрения. 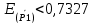 – погрешность является ничтожной и может быть исключена из рассмотрения. – погрешность является ничтожной и может быть исключена из рассмотрения. – погрешность не является ничтожной и не может быть исключена из рассмотрения. – погрешность не является ничтожной и не может быть исключена из рассмотрения.4.Вывод:При выполнении расчётно-графического задания, я применила теоретические знания на практике. Также, закрепила навыки расчёта результатов прямых измерений и исключения грубых ошибок. Улучшила навык оценки погрешностей косвенных измерений. |