1-Лабораторная_Метрология («Изучение методических погрешностей при прямых и косвенных измерениях». «МЕТРОЛОГИЯ» Автор В.Е. Эраст. 1-Лабораторная_Метрология («Изучение методических погрешностей п. Метрология
 Скачать 314 Kb.
|
|
Федеральное агентство образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) «иЗУЧЕНИЕ МЕТОДИЧЕСКИХ ПОГРЕШНОСТЕЙ ПРИ ПРЯМЫХ И КОСВЕННЫХ ИЗМЕРЕНИЯХ» «Метрология» Автор: В.Е. Эрастов Томск 1999 Лабораторная работа №1 Выполнил студент группы « 26 » мая 2008 г. Целью данной работы является изучение методических погрешностей при прямых и косвенных измерениях. 1. Прямые измерения. 1.1. Используя пакет Electronics Workbench соберем схему и реализуем ситуацию измерения постоянного тока, потребляемого активной нагрузкой. 1.2. Измерим действительное значение тока нагрузки, для этого подключим мультиметр в нужные точки и зафиксируем его показания в режиме измерения постоянного тока. 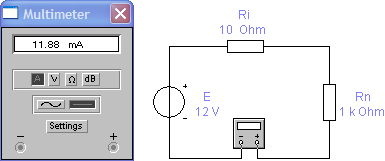 Рис. 1.2 1.3. Реализуем измерение тока нагрузки реальным амперметром, для чего изменим внутреннее сопротивление мультиметра, для начала примем RА = 0,1Rн. Зафиксируем показания мультиметра – в данном случае эти показания являются значением тока нагрузки, измеренным реальным прибором.  Рис. 1.3 Определим абсолютную и относительную (в %) погрешности измерения тока: Абсолютная погрешность:  Относительная погрешность:  Сделаем выводы: погрешность обусловлена тем, что реальный прибор имеет внутреннее сопротивление и, вследствие этого, при включении его в цепь, изменяются показания прибора. Погрешность называют методической потому, что она возникает из-за несовершенства метода измерений, из-за влияния средств измерений на объект, свойства которого измеряются. 1.4. Изменяя величину  от  до  и определяя каждый раз величину относительной методической погрешности, построим график зависимости методической погрешности от соотношения  , т.е.  .Полученные данные занесем в таблицу: Таблица 1.4
Построим график зависимости: 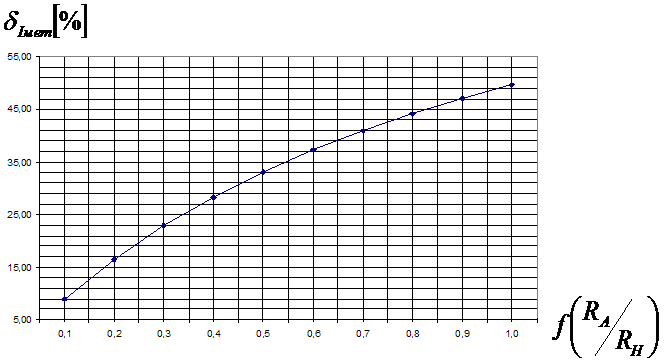 Рис. 1.4 График зависимости  1.5. Критерием, когда методическую погрешность можно не учитывать, может служить, например, условие,  или более жесткое, где  основная погрешность амперметра, определяемая его классом точности – в данном случае 1,0. Это приведенная аддитивная погрешность, и нормирующее значение выражено в единицах измеряемой физической величины (в данном случае мА). Это значит, что предел допускаемой основной погрешности амперметра ± 1,0 % .Следовательно, методическую погрешность можно не учитывать, если соблюдается условие:  . Рассчитаем внутреннее сопротивление амперметра:  , отсюда RA≤2 Ом. Таким образом, чтобы измерить сопротивление 1кОм, сопротивление амперметра не должно превышать 2 Ом. Необходимо выбирать амперметр с низким внутренним сопротивлением, которое будет меньше сопротивления измеряемой цепи в 500 и более раз.1.6. Реализуем ситуацию измерения падения напряжения постоянного тока на выходе резистивного делителя напряжения. Проведем мультиметром измерение напряжения на выходе делителя. Зафиксируем его показания, которые в этом случае будут действительным значением падения напряжения на участке цепи. 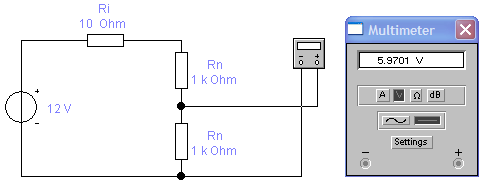 Рис. 1.6 1.7. Реализуем измерение напряжения в том участке цепи реальным вольтметром, для чего параллельно входным зажимам мультиметра включим сопротивление 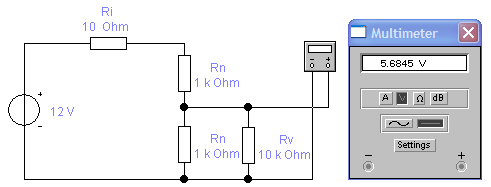 , имитирующее внутреннее сопротивление реального вольтметра. Выберем, для начала,  , где  - сопротивление участка цепи, падение напряжения на котором измеряется. Зафиксируем показания мультиметра.  Рис. 1.7 Определим абсолютную и относительную (в %) погрешности измерения напряжения реальным вольтметром: Абсолютная погрешность:  Относительная погрешность:  Сделаем выводы: погрешность обусловлена тем, что реальный прибор имеет внутреннее сопротивление и, вследствие этого, при включении его в цепь, изменяются показания прибора. Погрешность называют методической потому, что она возникает из-за несовершенства метода измерений, из-за влияния средств измерений на объект, свойства которого измеряются, т.е. из-за влияния вольтметра на электрическую цепь. 1.8. Изменяя величину  от  до  и определяя каждый раз величину относительной методической погрешности, построим график зависимости:  .Полученные данные занесем в таблицу: Таблица 1.8
Построим график зависимости:  Рис. 1.8 График зависимости  1.9. Критерием, когда методическую погрешность можно не учитывать, может служить, например, условие,  или более жесткое, где  основная погрешность вольтметра, определяемая его классом точности – в данном случае 1,0. Это приведенная аддитивная погрешность, и нормирующее значение выражено в единицах измеряемой физической величины (в данном случае В). Это значит, что предел допускаемой основной погрешности вольтметра ± 1,0 % .Следовательно, методическую погрешность можно не учитывать, если соблюдается условие:  . Рассчитаем внутреннее сопротивление вольтметра:  , отсюда RV≥500 кОм. Таким образом, чтобы измерить сопротивление 1кОм, сопротивление вольтметра не должно быть ниже 500 кОм. Необходимо выбирать вольтметр с высоким внутренним сопротивлением, которое будет больше сопротивления измеряемой цепи в 500 и более раз.2.Косвенные измерения. 2.1. Построим возможные схемы включения измерительных приборов (вольтметра и амперметра) для измерения сопротивления участка цепи  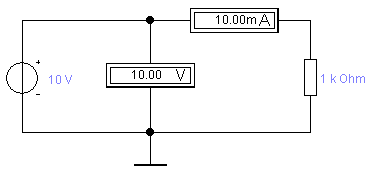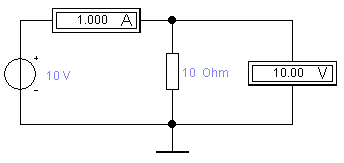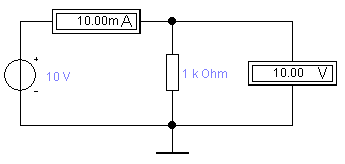на основании закона Ома. Внутреннее сопротивление источника питания  .    Рис. 2.1 2.2. Проведем измерение сопротивления Rx в каждом из возможных схем включения приборов дважды, задавая в качестве измеряемого сопротивления сначала RX1=10 Ом, а затем RX2=1000 Ом, и рассчитаем величину сопротивления Rx по показаниям приборов. Данные занесем в таблицу: Таблица 2.2
Рассчитанные значения Rx оказались одинаковыми для обеих схем. Так как в данном случае использовались идеальные измерительные приборы (RА = 0; RV = ∞), то обе схемы являются равнозначными, следовательно, ни одной схеме предпочтение отдать нельзя. 2.3. Для этих же схем включения приборов и тех же значений RX1 и RX2 реализуем процедуру измерения их реальными приборами. Для этого при измерении тока последовательно с мультиметром включим сопротивление RА=1 Ом, имитирующее внутреннее сопротивление амперметра, а при измерении напряжения параллельно входным зажимам мультиметра подключим сопротивление RV=5000 Ом, имитирующее внутреннее сопротивление вольтметра, как показано на рисунке: 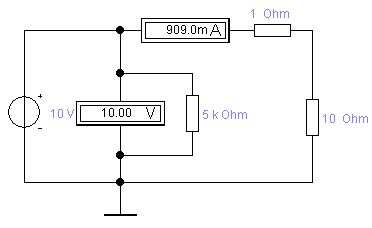   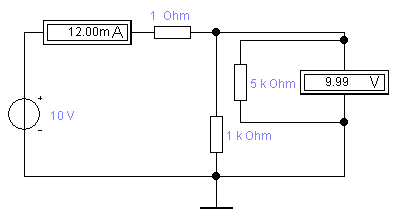 2.4. По показаниям приборов рассчитаем величины сопротивлений RX1изм и RX2изм для каждой из схем включения приборов. По закону Ома действительное сопротивление: RX=UR/IR. Определим абсолютную и приборную погрешности измерений для каждой из схем по формулам: Абсолютная погрешность:  Относительная погрешность:  Результаты занесем в таблицу: Таблица 2.4
Сделаем выводы: в первой схеме погрешность в большей степени зависит от сопротивления амперметра при измерении малых сопротивлений, во втором случае в большей степени от сопротивления вольтметра при измерении больших сопротивлений. Появившаяся погрешность в обоих случаях называется методической, т. к. погрешность возникает из-за несовершенства метода измерений и влияния средств измерения на электрическую цепь, свойства которой измеряются. 2.5. Проверим свой вывод о факторе, приводящем к методической погрешности, экспериментально. В каждой из схем включения приборов при неизменной величине измеряемого резистора RX необходимо провести ряд измерений его значения, изменяя каждый раз внутреннее сопротивление одного из приборов (например, RА) и оставляя неизменным внутреннее сопротивление другого (например, RV), а затем повторить эксперимент, изменяя RV и оставляя неизменным RА. Абсолютную и относительную погрешности рассчитаем по формулам: Данные занесем в таблицу: Таблица 2.5
По результатам эксперимента можно сделать следующие выводы: погрешность в первой схеме появляется из-за неточности определения напряжения на сопротивлении RX, т.к. вольтметр измеряет еще и напряжение на амперметре (а у амперметра свое внутреннее сопротивление ≠ 0). Следовательно, чем меньше будет внутреннее сопротивление амперметра по сравнению с измеряемым, тем меньше будет относительная погрешность. Во второй схеме амперметр показывает значение тока сопротивления RX и вольтметра (сопротивление вольтметра ≠ ∞), следовательно, чем больше будет сопротивление вольтметра по сравнению с измеряемым, тем меньше будет относительная погрешность. Одно и то же средство измерений при измерениях в одном случае может дать очень маленькую методическую погрешность, а при измерениях в другом – очень большую, лишающую измерения всякого смысла. Сравнивая величины погрешностей, можно сделать следующие выводы: - для измерения низкоомных сопротивлений следует отдать предпочтение второй схеме. - для измерения высокоомных – первой схеме. В таком сочетании измерительных приборов их взаимное влияние минимально. 2.6. Получим в общем виде аналитическую формулу для расчета относительной методической погрешности для каждой из схем измерения и определим, начиная с какого значения RX, методическая погрешность для каждой из схем будет удовлетворять условию Rмет 1%. Внутренние сопротивления приборов те же: RА=1 Ом, RV=5000 Ом. Аналитическая формула для расчета относительной методической погрешности для первой схемы: RР = RX + RА RР – сопротивление, полученное расчетным путем.   Методическая погрешность для первой схемы будет удовлетворять, условию Rмет 1% начиная со значения RX ≥ 100 Ом. Аналитическая формула для расчета относительной методической погрешности для второй схемы:  RР – сопротивление, полученное расчетным путем. 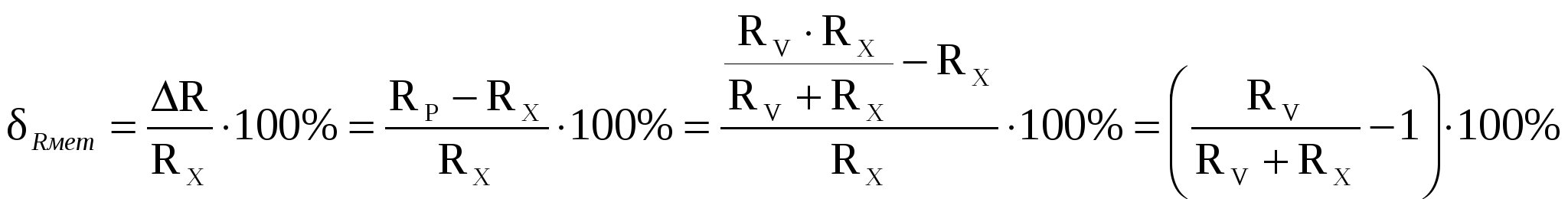  Методическая погрешность для первой схемы будет удовлетворять, условию Rмет 1% начиная со значения RX 49,5 Ом. |
