Министерств
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
|
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)» Институт Экономики и Финансов Кафедра «Информационные системы цифровой экономики» Курсовая работа по дисциплине «Методы оптимальных решений» на тему «Модели организации и планирования производства» Вариант №1 Выполнил(а): Студент гр.ЭСБ-241 Александровский С.А. Проверил: доц. Фроловичев А.И. Москва – 2023 Содержание ВВЕДЕНИЕ 1 ОСНОВНАЯ ЧАСТЬ 2 Кейс-задание №1 2 графический метод; 3 использование надстройки «Поиск решения» MSExcel. 4 Кейс-задание №2B 5 симплекс-метод 5 использование надстройки «Поиск решения» MSExcel 6 дополнительные вопросы оптимальности 7 А). Определить дефицитные и избыточные ресурсы; 8 Б). Насколько можно уменьшить запасы избыточных ресурсов, чтобы программа производства не пострадала? 9 В). Как изменится производственная программа и прогнозируемая прибыль при увеличении запасов дефицитных ресурсов на 5% 10 Г). Как изменится производственная программа при увеличении прибыли, получаемой от стали марки С, на N единиц, где N – число букв в фамилии студента, выполняющего курсовую работу 10 ЗАКЛЮЧЕНИЕ 11 СПИСОК ЛИТЕРАТУРЫ 12 ВВЕДЕНИЕ В процессе управления используется множество разных образов, подходов и приемов, которые позволяют упорядочить, целенаправленно и эффективно организовать выполнение функций, этапов, процедур и операций, необходимых для принятия решений. В совокупности они выступают как методы управления, под которыми понимаются образы осуществления управленческой деятельности, которые создаются для постановки и достижения ее цели. Математические методы занимают особое место в управлении, поскольку на их основании происходит взаимное обогащение теории и практики управления. Действительно, отвечая на вопрос, как выполнять ту или другую управленческую работу, методы позволяют сформировать систему правил, приемов и подходов, которые сокращают расходы времени и других ресурсов на реализацию. Оптимальные (эффективные) решения позволяют достигать цели при минимальных затратах трудовых, материальных и сырьевых ресурсов. В классической математике методы поиска оптимальных решений рассматривают в разделах, связанных с изучением экстремумов функций, в математическом программировании. Методы оптимальных решений является одним из разделов исследования операций, используемого для решения практических организационных задач. Задачи математического программирования находят применение в различных областях человеческой деятельности, где необходим выбор одного из возможных образов действий (программ действий). Среди методов математического программирования наиболее полно разработанными и распространенными в производственной практике являются методы линейного программирования. Целью данной курсовой работы является овладение математическими методами решения экономических задач. Линейное программирование — это наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения. Для решения задач линейного программирования составляется математическая модель задачи и выбирается метод решения. По типу решаемых задач методы разделяются на универсальные и специальные. ОСНОВНАЯ ЧАСТЬ Кейс-задание №1 Предприятие может выпускать две марки стали: сталь марки А и сталь марки B. Норма расхода сырья, времени работы оборудования и затрат на электроэнергию, которые необходимы для производства одной тонны каждого изделия, приведены в таблице. Недельные запасы ресурсов, которыми располагает предприятие, ограничены. По сырью эти ограничения обусловлены финансовыми средствами, емкостью складских помещений, логистическими ограничениями и т.д., по оборудованию – плавильными мощностями и трудовыми ресурсами, по электроэнергии – техническими и финансовыми причинами. Размеры запасов и прибыль от реализации продукции в у.е. за 1 тонну приведены в таблице 1. Исходная таблица
Таблица со значениями из варианта
Требуется сформировать недельную производственную программу (определить объемы выпуска каждого вида продукции), при которой прибыль от реализации будет максимальной. графический метод; Построение математической модели. Критерий оптимальности – максимальный доход. Переменные решения: х1 – сталь марки A (тонн); х2 – сталь марки B (тонн); Цель – максимизация прибыли, получаемая при двух видов стали. Целевая функция: Z(X) = 90х1+140х2max Ограничения по запасам ресурса на три вида продукции. Левая часть ограничения по нормам расхода ресурсов представляет собой сырье, оборудование и электроэнергию, затрачиваемые на производство объема выпуска каждого вида крепежных изделий х1, х2. Правая часть ограничения – это их запас ресурса. Получаем следующие ограничения:  - по сырью: - по сырью:0,55х1 + 0,75х2 ≤ 3220 - по оборудованию: 0,45х1 + 0,6х2 ≤ 2130 - по электроэнергии: 0,4х1 + 0,7х2 ≤ 2125 Вид математической модели: Z(X) = 90х1+140х2 max 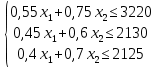 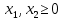 Для построения графической системы необходимо решить неравенства. Для этого приравняем каждое из неравенств и решим их по отдельности. 1) 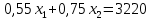
2) 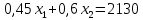
3) 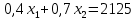
Исходя их нашей целевой функции задачи Z(X) = 90х1+140х2 max, можем найти вектор-градиент. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации Z(X). Начало вектора – точка (0; 0), конец – точка (90;140). grad = (90;140) 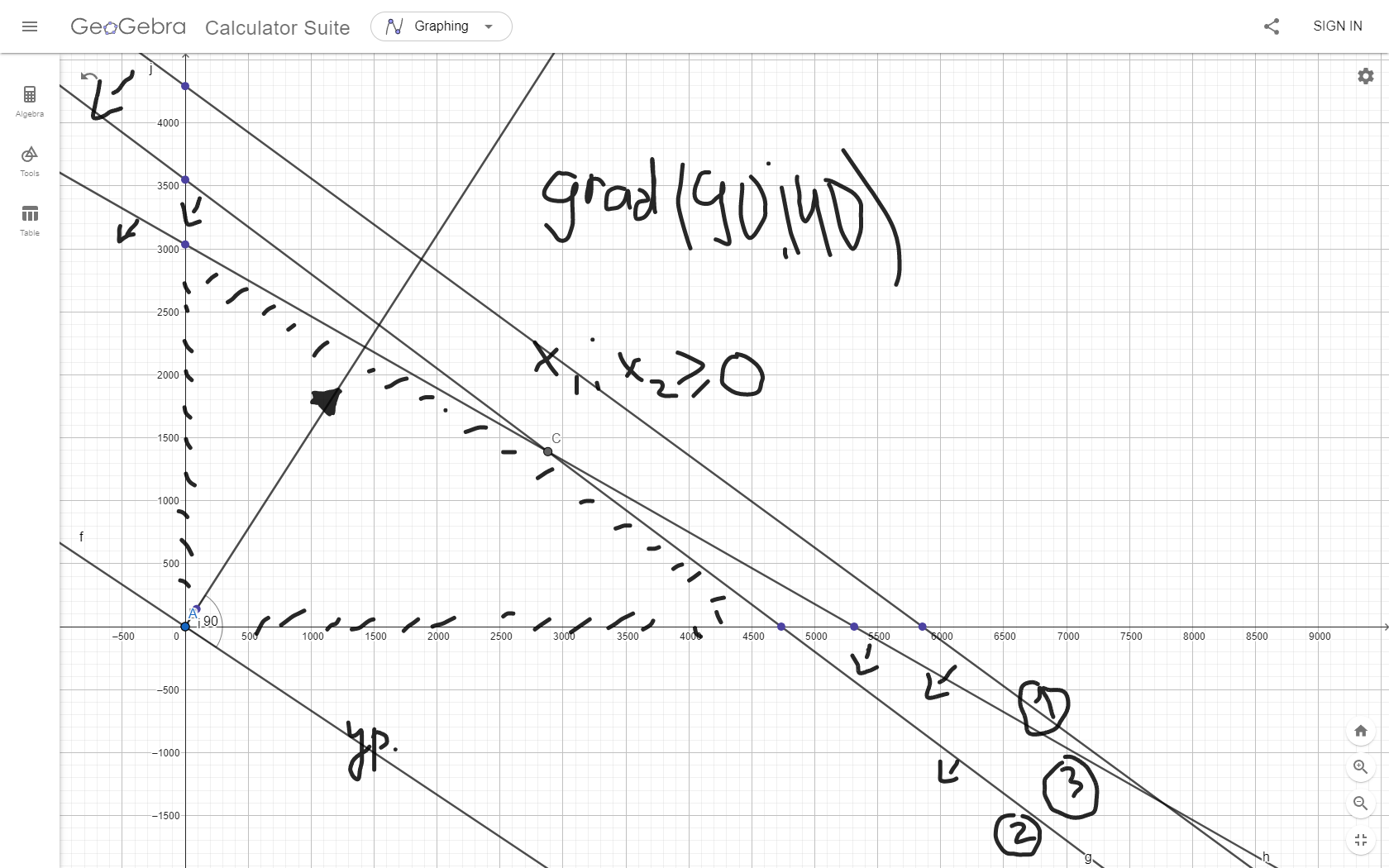 (Графическое решение) 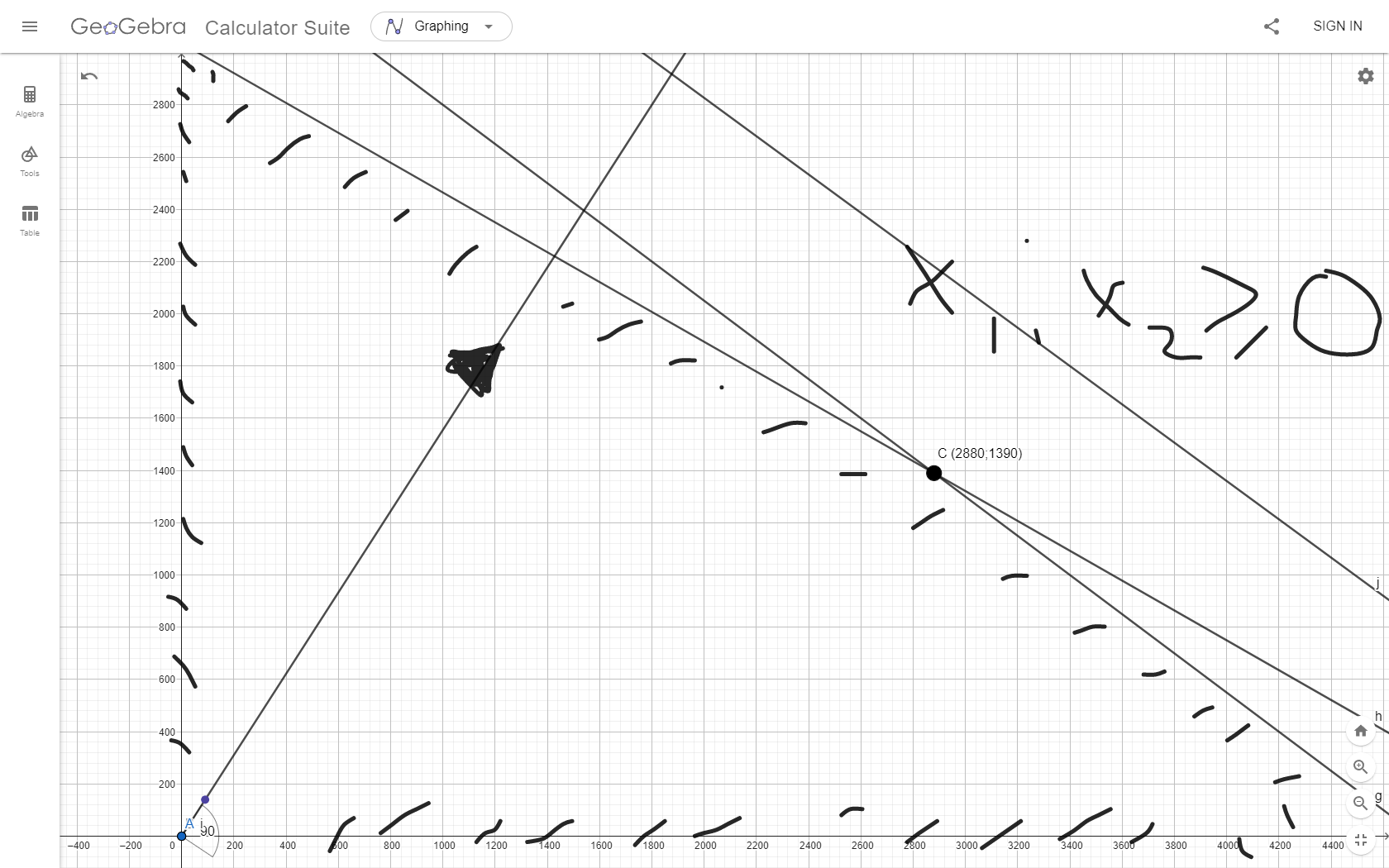 (Выбор точки максимума)  Если вести линию уровня перпендикулярно вдоль нашего grad (90;140), то мы получим точку максимума C с координатами (2880;1390). Данная точка находится на пересечении 2 и 3 прямых. Решив систему уравнений из уравнений, мы проверим данную точку. Если вести линию уровня перпендикулярно вдоль нашего grad (90;140), то мы получим точку максимума C с координатами (2880;1390). Данная точка находится на пересечении 2 и 3 прямых. Решив систему уравнений из уравнений, мы проверим данную точку.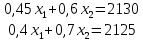 Решив систему уравнений, получим: 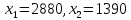 Теперь найдем максимальное значение функции: Z(X) = 90х1+140х2 max 90*2880+140*1390 = 453800 Ответ: 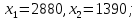 Z(X)= 453800 Z(X)= 453800использование надстройки «Поиск решения» MSExcel. Построив математическую модель, можно перейти к построению табличной модели. Для этого введем данные – параметры, которые характеризуют выпуск крепежных изделий, в единую таблицу. 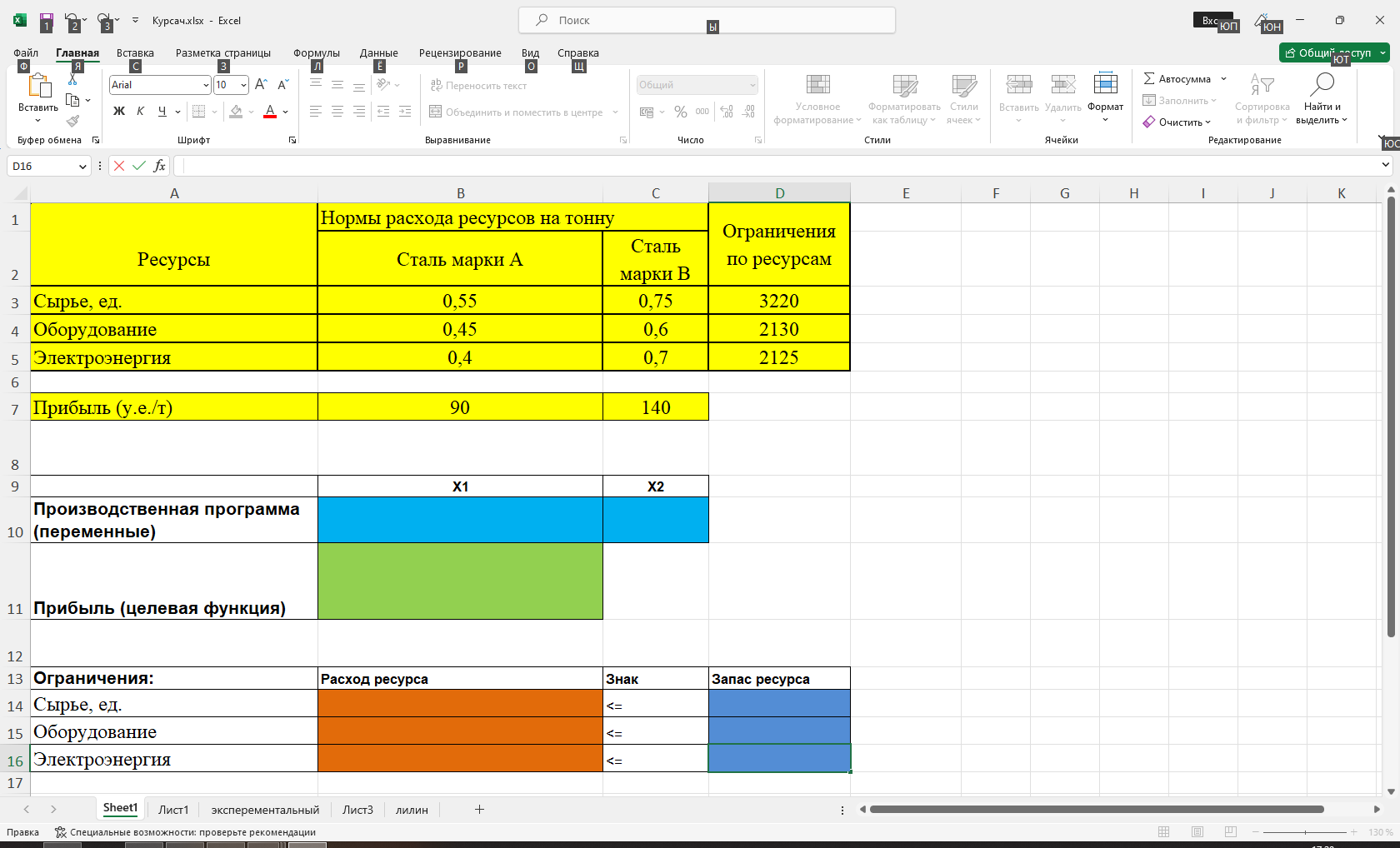 (Исходные данные в табличной модели) В колонке «Запас ресурса» указаны ограниченные месячные запасы ресурсов, которыми располагает предприятие. Целевая функция. В ячейке В11 будет отображаться значение целевой функции. Формула, по которой это значение будет рассчитано, определяется выражением: 90х1+140х2 Используя обозначения соответствующих ячеек в Excel, получим следующее: =СУММПРОИЗВ(B10:C10;B7:C7) Ограничения задачи представляют собой сумму произведений каждой из ячеек переменных (B10, C10) на соответствующую ячейку для коэффициентов конкретного ограничения (B7, C7). Таким образом, для первого ограничения в ячейку В14 будет введена формула: =СУММПРОИЗВ($B$10:$C$10;B3:C3), где символ $ означает, что при копировании этой формулы в другие места листа Excel номер строки 10 не изменится. Скопируем эту формулу в ячейки В15 и В16. В формуле будет меняться только номер строки во втором массиве. Этот номер является строкой, где записано ограничение. 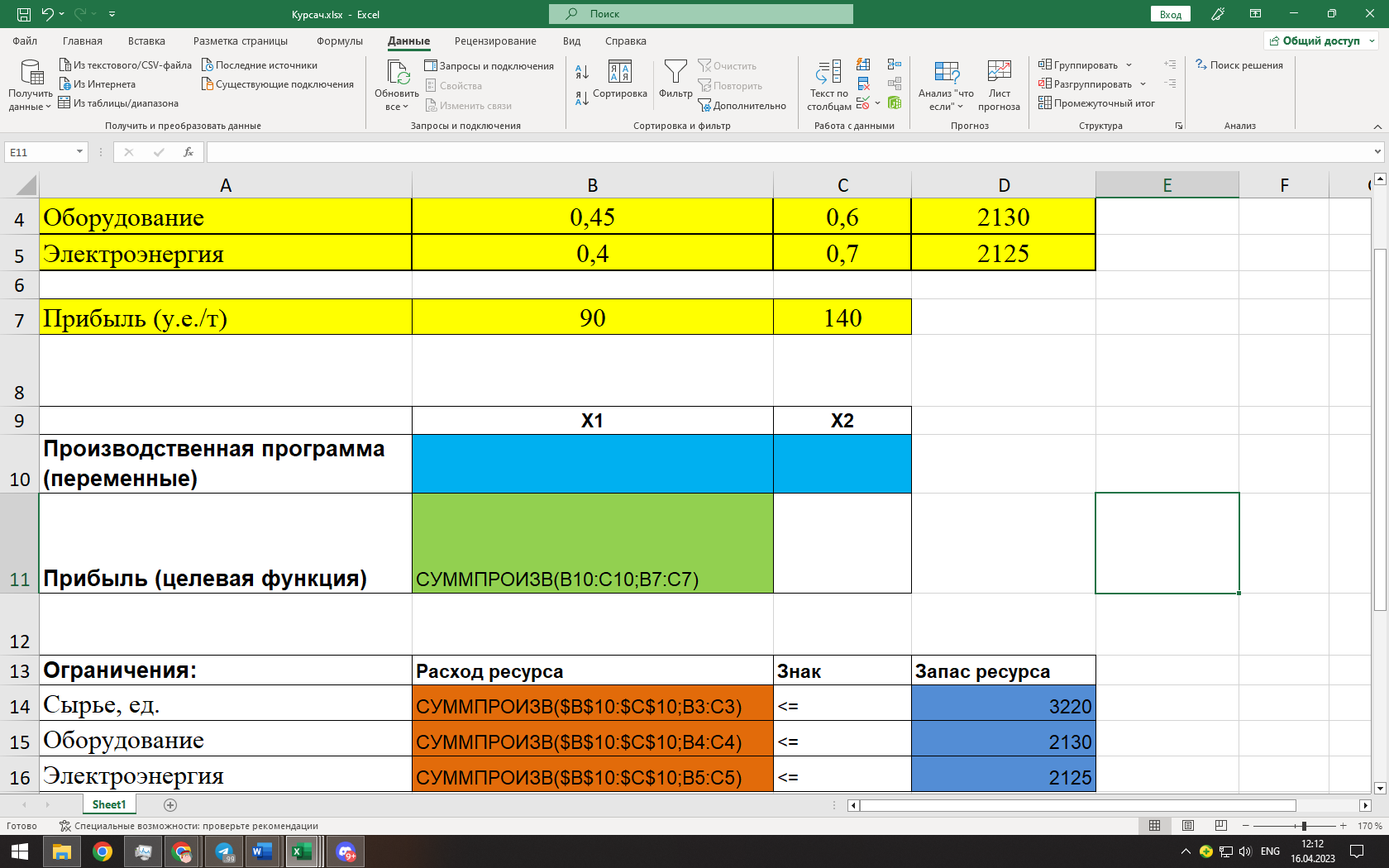 (Ячейки с заполненными формулами) С помощью надстройки «Поиск решения» найдем решение данной задачи. В диалоговом окне «Поиска решения» требуется ввести необходимые параметры. 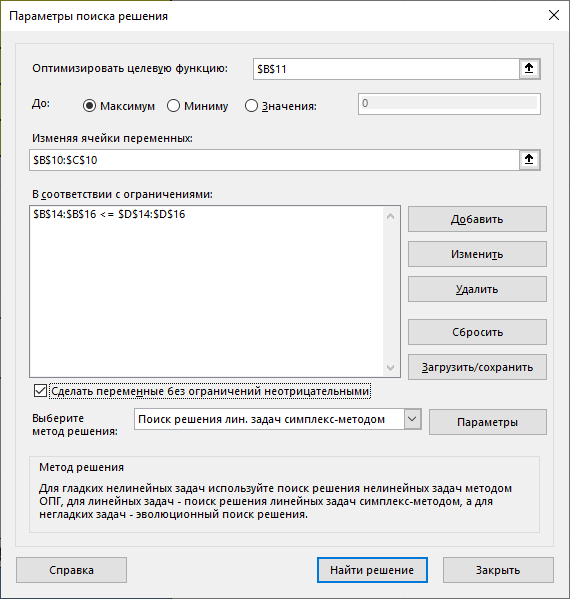 (Задача параметров для поиска решений)  (Уведомление о нахождении решения) 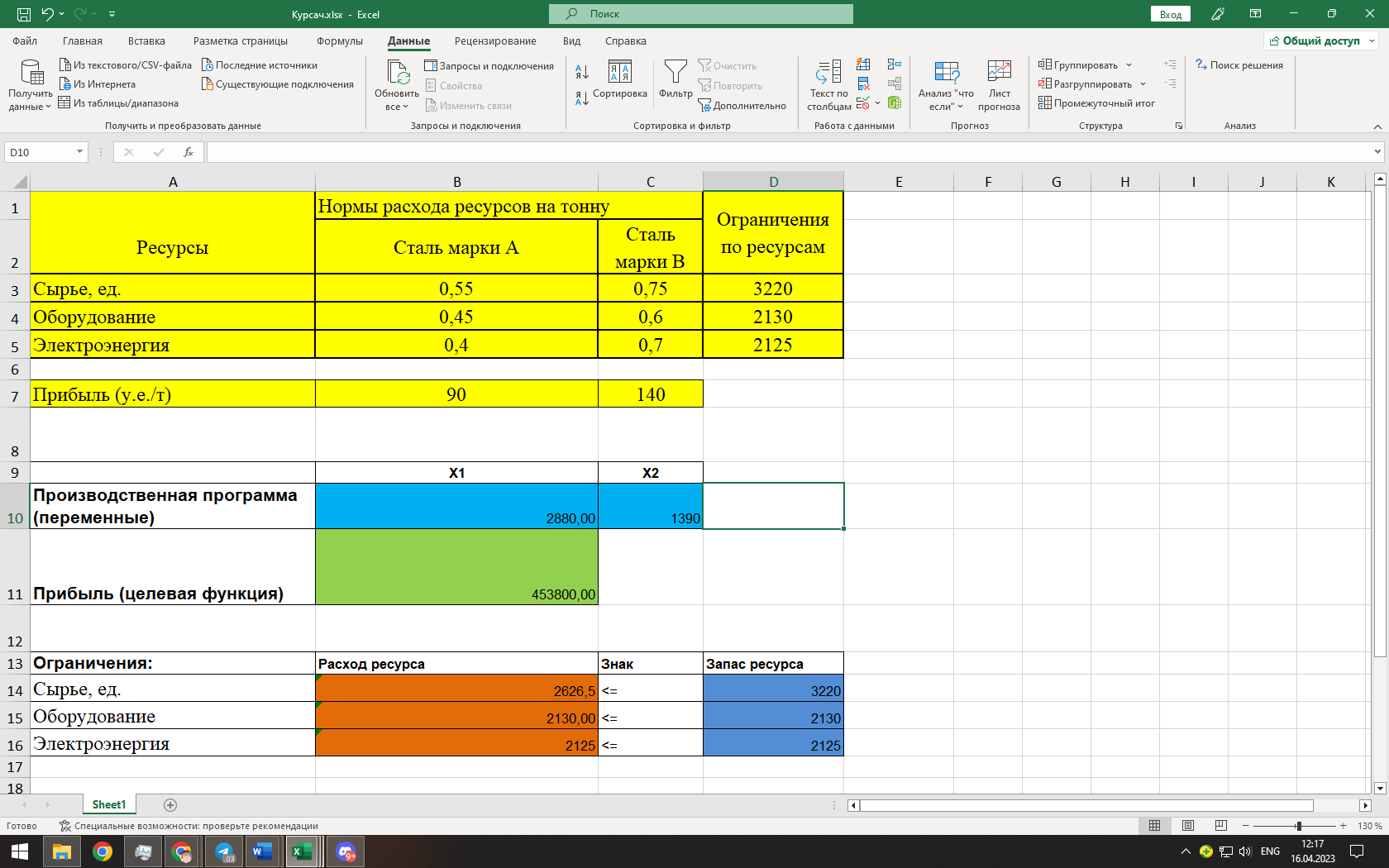 (Результат поиска решений) Вывод: таким образом в ячейках получается оптимальное решение по производственной программе. При производстве 2880 тонн стали марки A и 1390 тонн стали марки B производство получит максимальную прибыль. Кейс-задание №2B Предприятие может выпускать три марки стали: сталь марки А, сталь марки B и сталь марки C. Норма расхода сырья, времени работы оборудования и затрат на электроэнергию, которые необходимы для производства одной тонны каждого изделия, приведены в таблице.
симплекс-метод Построение математической модели. Критерий оптимальности – максимальный доход. Переменные решения: х1 – Сталь марки A х2 – Сталь марки B х3 – Сталь марки C Цель – максимизация прибыли, получаемая при реализации крепежных изделий: шайб, гаек и болтов. Таким образом, суммарная прибыль, то есть целевая функция: Z(X) = 90х1+140х2+200х3 max Ограничения по запасам ресурса на три вида продукции. Левая часть ограничения по нормам расхода ресурсов представляет собой сырье, оборудование и электроэнергию, затрачиваемые на производство объема выпуска каждого вида крепежных изделий х1, х2, х3. Правая часть ограничения – это их запас ресурса. Получаем следующие ограничения: 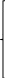 - по сырью: - по сырью:0,55х1 + 0,75х2+1,1х3 ≤ 3220; - по оборудованию: 0,45х1 + 0,6х2 +1х3 ≤ 2130; - по электроэнергии: 0,4х1 + 0,7х2 +0,9х3 ≤ 2125 Вид математической модели: Z(X) = 90х1+140х2+200х3 max 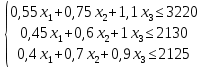 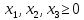 Приведем задачу линейного программирования к каноническому виду: 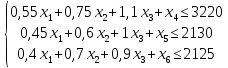 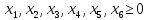 Следовательно: Z1(X)=0-(90х1+140х2+200х3) min Первый опорный план: 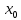 = (0,0,0,3220,2130,2125) = (0,0,0,3220,2130,2125)Базисное решение с помощью следующей симплекс-таблицы:
Нашли генеральный элемент – 1, так как в строке Z выбираем положительное число (у нас число 200 – выбираем столбец х3), а в столбце х3, не считая строки Z, выбираем то значение, для которого отношение к нему свободного члена минимально (2130/1 – минимальное значение). В новом допустимом базисном решении х3 и х5 изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:
Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты. Определяем генеральный элемент в новой таблице – 0,16. В новом допустимом базисном решении х2 и х6 изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:
Текущий опорный план неоптимален, так как в индексной строке вновь встречается отрицательный коэффициенты. Значит нам предстоит повторный пересчет. Определяем генеральный элемент в новой таблице – 0,47. В новом допустимом базисном решении х2 и х6 изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:
Далее генеральный столбец выбрать нельзя. Значит, оптимальное решение имеет вид: Хопт= (2880; 1390;0) Zmin=-4538000 Zmax= 90*2880 +140*1390 +200*0=453800 Вывод: при объеме выпуска 2880 тонн стали марки A, 1390 тонн стали марки B и 0 тонн стали марки C максимальная прибыль от реализации составит 453800 у.е. использование надстройки «Поиск решения» MSExcel Построив математическую модель, можно перейти к построению табличной модели. Для этого введем данные – параметры, которые характеризуют выпуск стали, в единую таблицу. 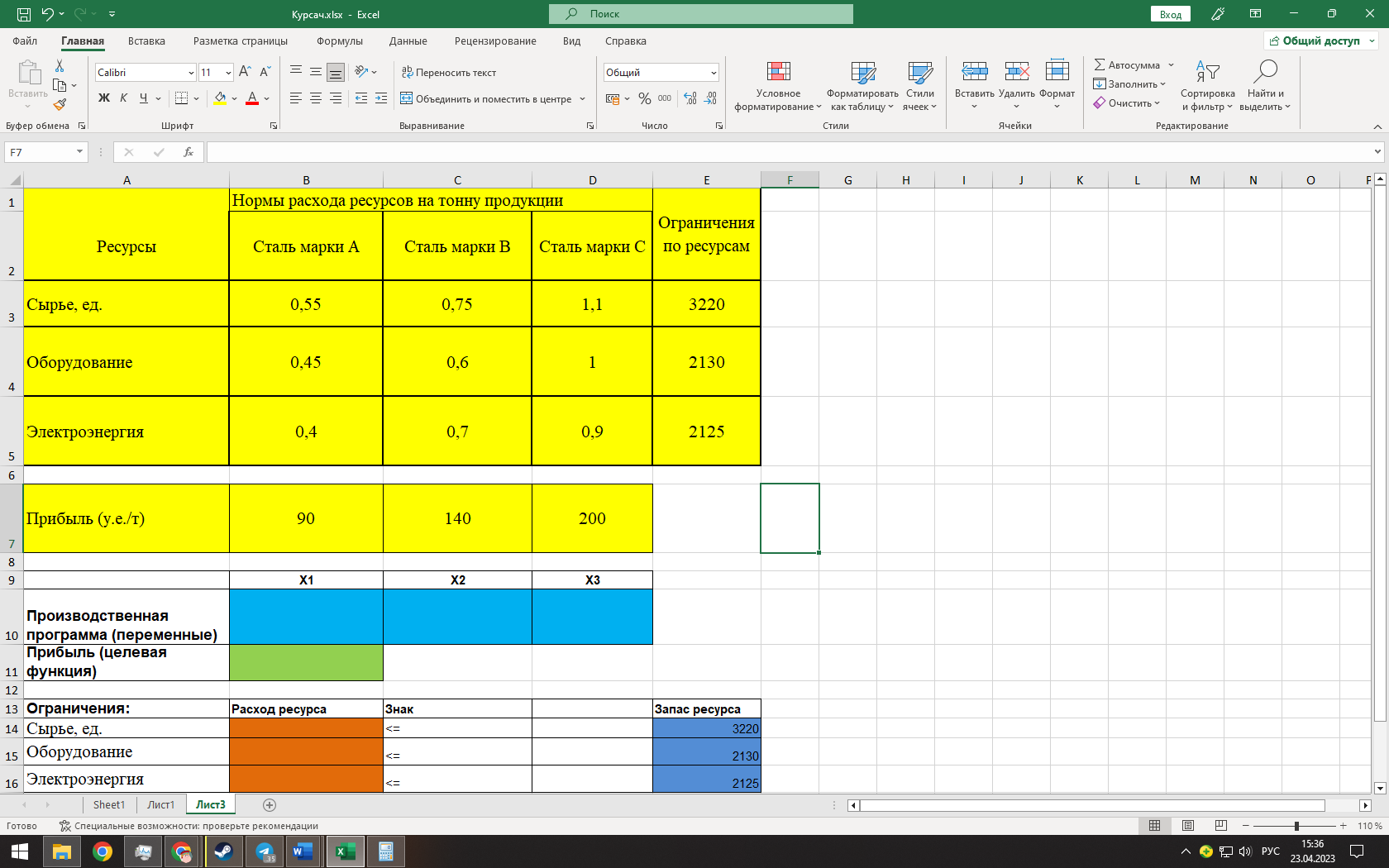 (Исходные данные в табличной модели) В колонке «Запас ресурса» указаны ограниченные месячные запасы ресурсов, которыми располагает предприятие. Целевая функция. В ячейке В11 будет отображаться значение целевой функции. Формула, по которой это значение будет рассчитано, определяется выражением: 90х1+140х2+200х3 Используя обозначения соответствующих ячеек в Excel, получим следующее: =СУММПРОИЗВ(B10:D10;B7:D7) Ограничения задачи представляют собой сумму произведений каждой из ячеек переменных (B10, D10) на соответствующую ячейку для коэффициентов конкретного ограничения (B7, D7). Таким образом, для первого ограничения в ячейку В14 будет введена формула: =СУММПРОИЗВ($B$10:$D$10;B3:D3), где символ $ означает, что при копировании этой формулы в другие места листа Excel номер строки 10 не изменится. Скопируем эту формулу в ячейки В15 и В16. В формуле будет меняться только номер строки во втором массиве. Этот номер является строкой, где записано ограничение. 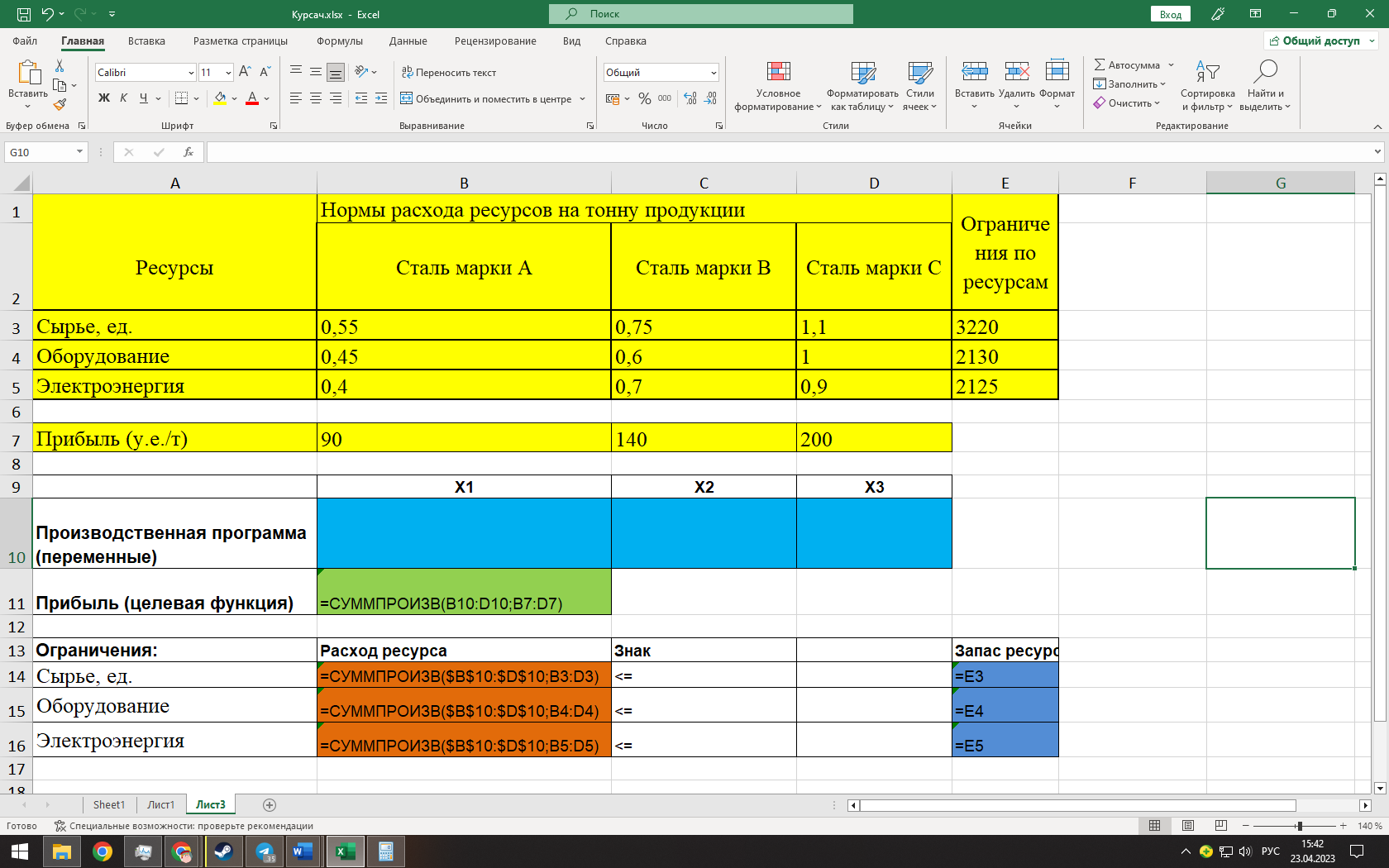 С помощью «Поиска решения» найдем решение данной задачи. В диалоговом окне «Поиска решения» требуется ввести необходимые параметры. 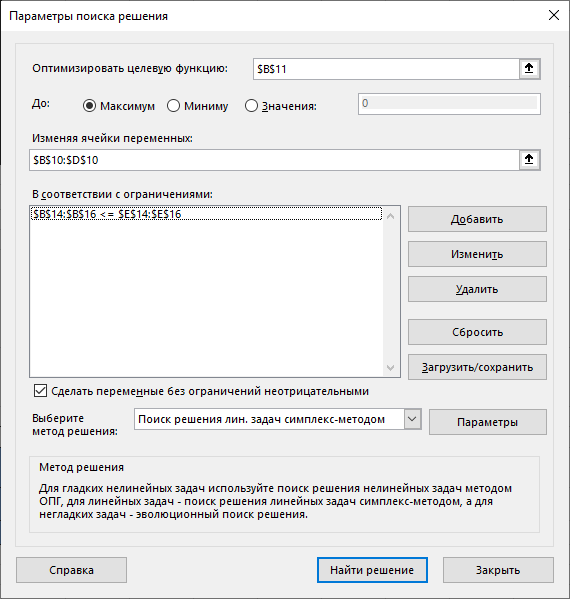 (Задача параметров для поиска решений) 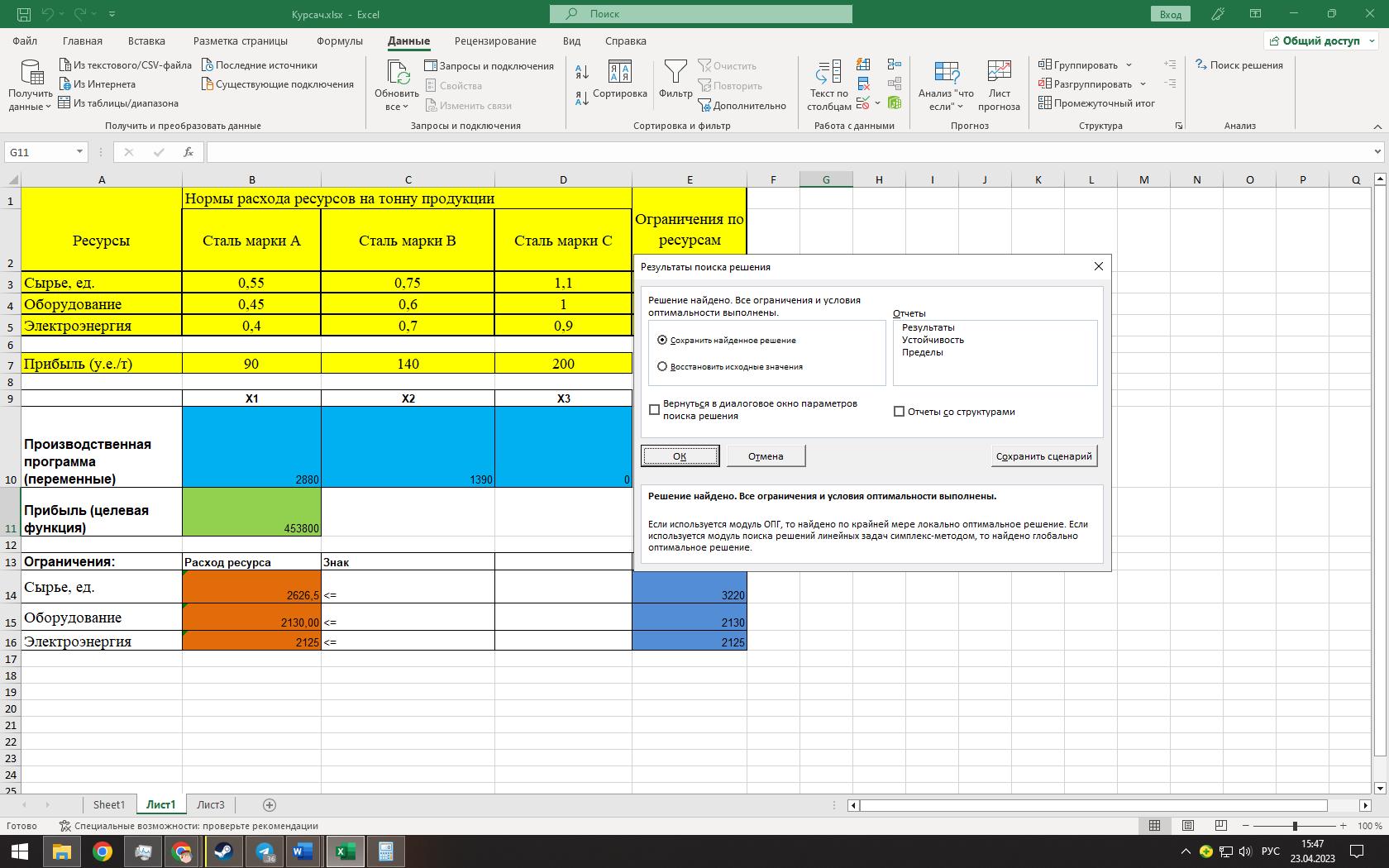 (Выполнение поиска решений) 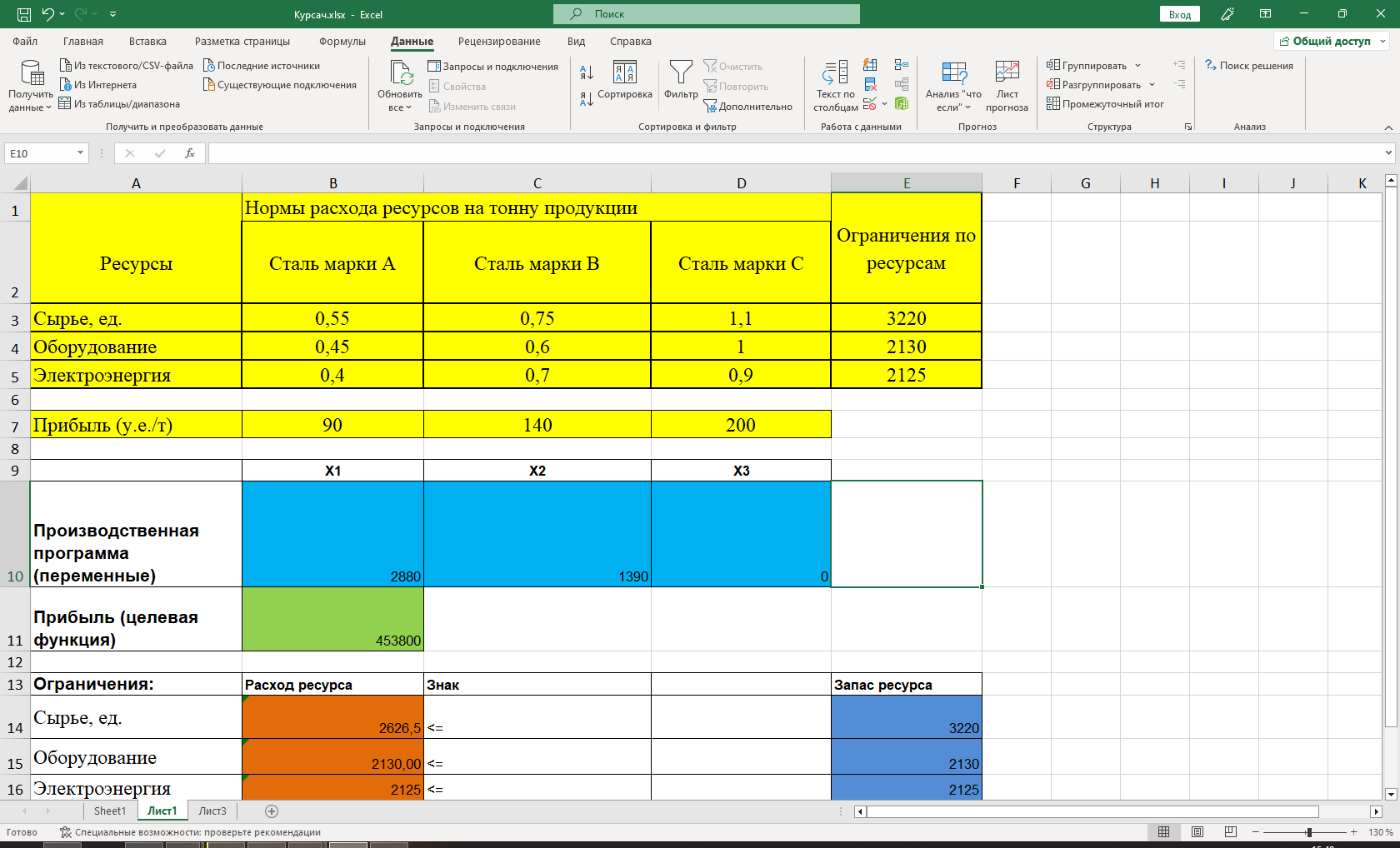 (Результаты поиска решений) Вывод: при объеме выпуска 2880 тонн стали марки A, 1390 тонн стали марки B и 0 тонн стали марки C максимальная прибыль от реализации составит 453800 у.е. дополнительные вопросы оптимальности А). Определить дефицитные и избыточные ресурсы; Дефицитные ресурсы — это те ресурсы, которые в соответствии с экономическим принципом нехватки ресурсов или законом о нехватке ресурсов находятся в ситуации ограниченной доступности. Избыточный ресурс — это ресурс, который имеется в избытке или излишке в системе, и может не может быть использован полностью. Для полноценного понимания, какие ресурсы являются избыточными/дефицитными, проведем анализ. Удобно будет проанализировать уже готовое решение, которое было представлено нам в предыдущем пункте данной работы. Основываясь на нем, можно заметить, что все марки стали используют все три вида ресурсов, а именно: сырье, оборудование и электроэнергия. Однако данные ресурсы распределены неравномерно, что-то расходуется в большой степени, что-то в меньшей. Также стоит учитывать запасы ресурсов, тот максимум, который есть на складе и может быть реализован. Более того, нужно понимать, что даже при достатке двух ресурсов, но отсутствии одного сталь не может быть произведена. Проанализировав данную информацию, можно перейти к определению избыточных и дефицитных ресурсов. Посмотрев на расход ресурсов и их запасы, мы можем заметить, что такие ресурсы как Электричество и Оборудования полностью израсходованы и их запасы полностью истощены.
В тоже время видим, что наше производство имеет остатки по Сырью. Его расход не превышает запасы, наоборот он меньше. Таким образом процесс производства прерывается из-за лимита по Оборудованию и Электроэнергии, но не из-за Сырья, это говорит о том, что если увеличить запасы Оборудования и Электроэнергии, но не увеличивать запасы Сырья, то мы все равно сможем произвести дополнительные единицы продукции. Вывод: Дефицитные ресурсы: Оборудование; Электроэнергия. Избыточные ресурсы: Сырье Б). Насколько можно уменьшить запасы избыточных ресурсов, чтобы программа производства не пострадала? Как мы выяснили в предыдущем пункте данной работы, наше производство, создающее продукцию из нескольких видов ресурсов, не полностью использует все из них. Это означает, что часть запасов может быть уменьшена для того, чтобы использовать ресурсы полностью, не оставляя их на складе. Такой подход может быть оправдан на реальном производстве при, ведь это может помочь уменьшить издержки на закупку сырья, позволит отказаться от аренды дополнительных складских помещений и т.д. Перейдем непосредственно к переоценке запасов и их оптимизации. Как было установлено ранее, Сырье является избыточным ресурсом, это означает, что запасы можно ограничить без ущерба производству. Сами запасы по изначальному условию задачи равны 3220 единиц. А использование при оптимальном производстве, то есть максимизации прибыли равен 2626,5 ед. Итого мы имеем: 3220-2626,5=593,5 593,5 это те самые избыточные единицы, которые не участвуют в производстве и от них можно отказаться, и это не скажется на производственной программе и, следовательно, на нашей прибыли. 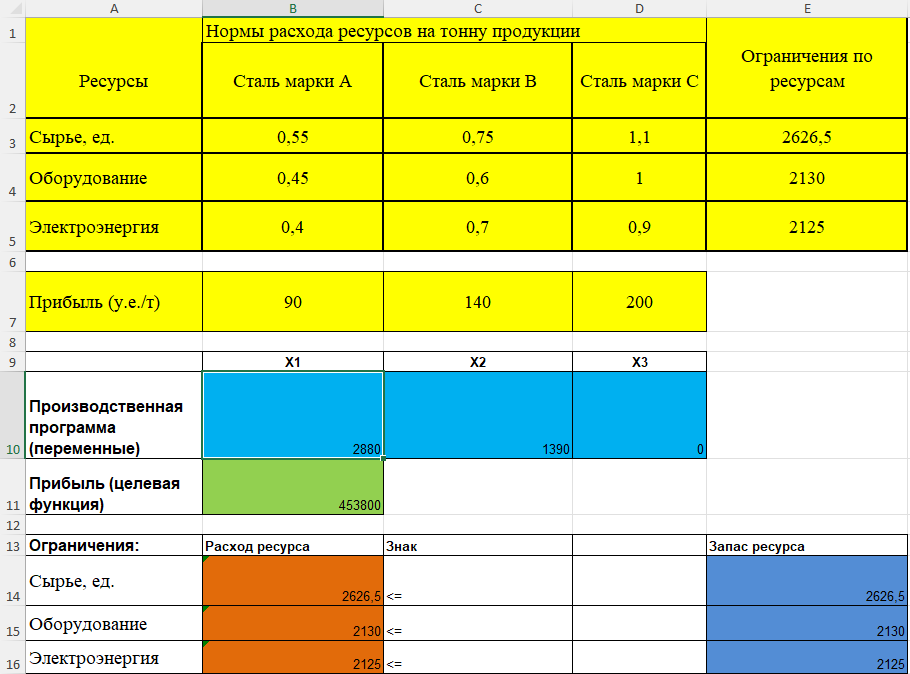 (Производство при сокращении избыточных ресурсов) Как видим при уменьшение запасов Сырья на 593,5 единицы производственная программа никак не изменилась, прибыли и количество произведенных единиц также не пострадало. Вывод: при уменьшение такого избыточного ресурса как Сырье на максимально возможные 593,5 единицы, производственная программа и прибыль не меняются. В). Как изменится производственная программа и прогнозируемая прибыль при увеличении запасов дефицитных ресурсов на 5% Нами было уже установлено, что дефицитными ресурсами являются Оборудование и Электроэнергия.
Таким образом мы получаемы таблицу с изменением начальных параметров, а именно запасов. Это позволит произвести больше продукции, а следовательно, увеличить нашу прибыль. 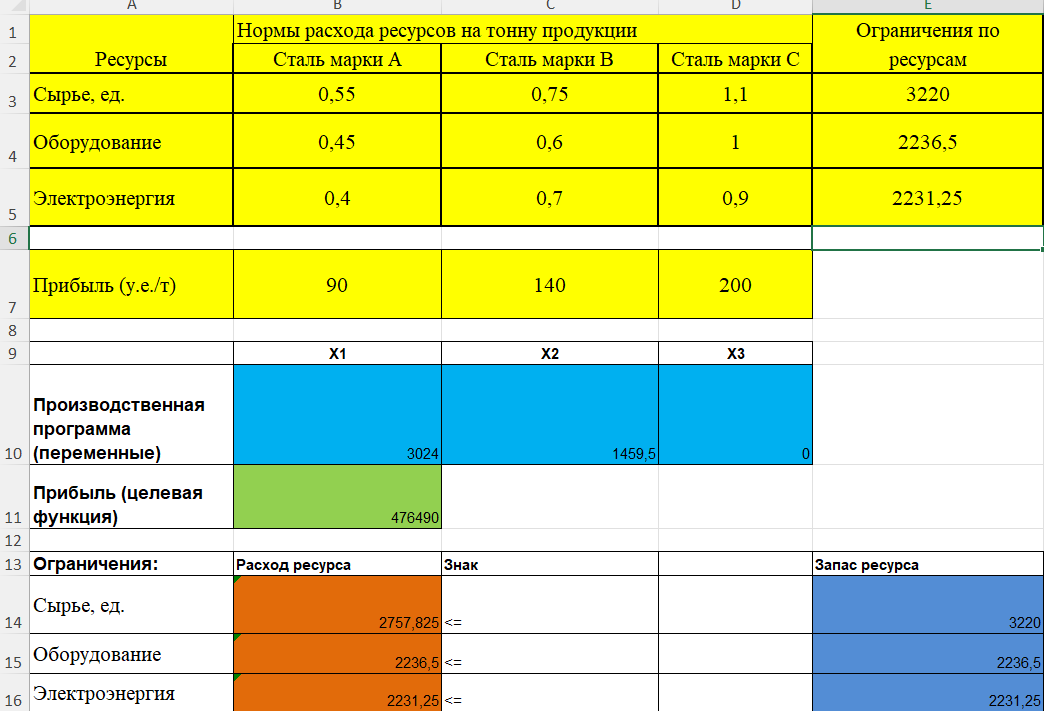 (Измененная программа производства) Таким образом мы видим, что при незначительном увеличении запасов ресурсов, которых нахватает при производстве, наша производственная программа меняется. Количество произведенных единиц продукции увеличивается, а вместе с ними и полученная прибыль. Вывод: при увеличении запасов дефицитных ресурсов на 5% мы получаем рост произведенных единиц Стали марки А на 144 единиц; Стали марки B на 69,5; количество единиц Стали марки С осталось нулевым, а прибыль выросла на 22690 условных единиц за тонну. Г). Как изменится производственная программа при увеличении прибыли, получаемой от стали марки С, на N единиц, где N – число букв в фамилии студента, выполняющего курсовую работу Изначальной прибылью от Стали марки С является 200 условных единиц за тонну. При увеличении этого показателя производственная программа может существенно измениться, перейдя на более оптимальное и выгодное производство при изменении ситуации на рынке. Моя фамилия Александровский — это 15 букв. Значит наша N=15. Итого мы имеем: 200+15=215 (у.е./т) 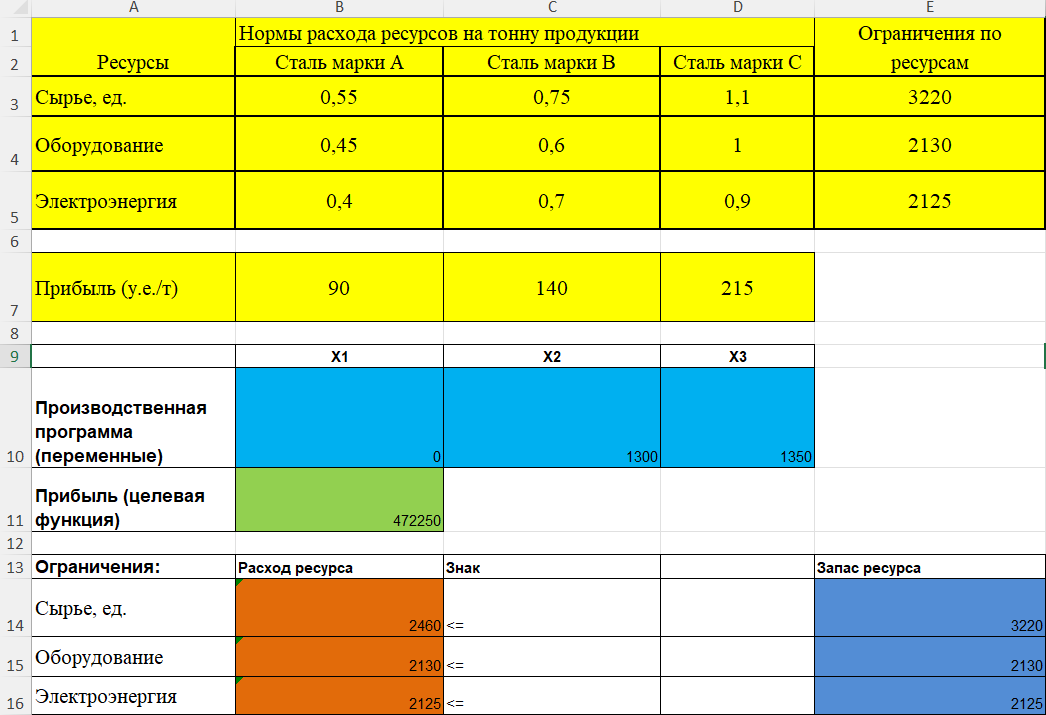 (Измененная программа производства) После анализа изменений производственной программы мы видим, что приоритет производства сместился. Раньше мы полностью отказывались от производства Стали марки С, так как она была не рентабельна и не окупала затраченных на нее ресурсов в той же мере как и другие марки стали, но после роста ее цены при реализации на 15 единиц, производственная программа поставила приоритет на нее, полностью отказавшись от Стали марки А, ранее производя ее в приоритете. Таким образом, можно сказать, что при небольших колебаниях на рынке, которые как удешевляют стоимость сырья, так и увеличивают прибыль от продажи изделия, производственная программа должна адаптироваться под изменения, постоянно приспосабливаться к ним и искать оптимальное решение. Вывод: при увеличении цены за тонну Стали марки С до показателя в 215 условных единиц мы получаем отказ от производства Стали марки А, уменьшение производства Стали марки B на 90 единиц и увеличение производства Стали марки C с 0 до 1350 единиц. Что приводит к увеличению прибыли на 6300 у.е. ЗАКЛЮЧЕНИЕ В курсовой работе рассмотрены варианты решений оптимизационных экономических задач методами линейного программирования. Метод математического программирования является основным инструментом описания оптимальных решений. Оптимальным решением считается такой способ действия, который в наибольшей степени способствует достижению поставленной в задаче цели. Наиболее простыми и лучше всего изученными среди задач математического программирования являются задачи линейного программирования, изучающие методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием. В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов. Современные методы линейного программирования достаточно надежно решают задачи общего вида с несколькими тысячами ограничений и десятками тысяч переменных. Для решения сверхбольших задач используются уже, как правило, специализированные методы. В данной курсовой работе были рассмотрены и решены основные задачи линейного программирования по оптимизации производства. Для решения данных задач были применены методы линейного программирования, а именно: графический метод и симплекс-метод, а также использовалась надстройка Microsoft Excel «Поиск решения». Таким образом выполнение данной курсовой работы показывает, что линейное программирование и методы оптимальных решений могут быть использованы при управление производственными процессами компаний для ускорения и повышения эффективности деятельности организации, а также для увеличения прибыли, что является целью всех коммерческих организаций. СПИСОК ЛИТЕРАТУРЫ Ишханян М.В., Фроловичев А.И. Методы оптимальных решений: учебное пособие. – М.: МИИТ, 2015. – 132 с. Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др.]; под ред. проф. H.Ш. Кремера. - 3-е изд. - М.: ЮНИТИ-ДАНА, 2010. – 479 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
