графический метод. графичекий метод. max, при системе ограничений
 Скачать 44.65 Kb. Скачать 44.65 Kb.
|
|
а)F = x1+3x2 → max, при системе ограничений: x1+2x2≤8, (1) x1+x2≤6, (2) 4x1+3x2≥3, (3) x1 ≥ 0, (4) x2 ≥ 0, (5) 1). Построим область допустимых решений, т.е. решим графически систему неравенств.  2. Границы области допустимых решений. 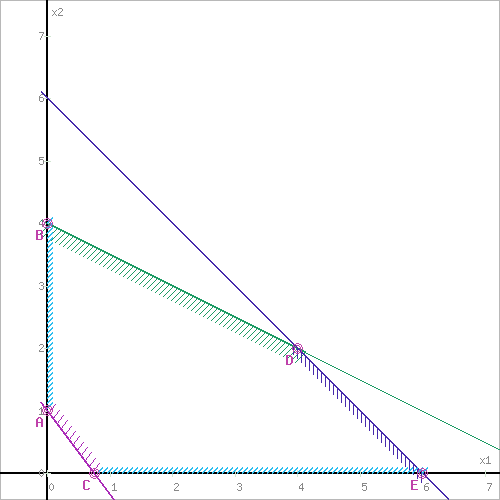 3. Построим прямую, отвечающую значению функции F = x1+3x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (1;3). 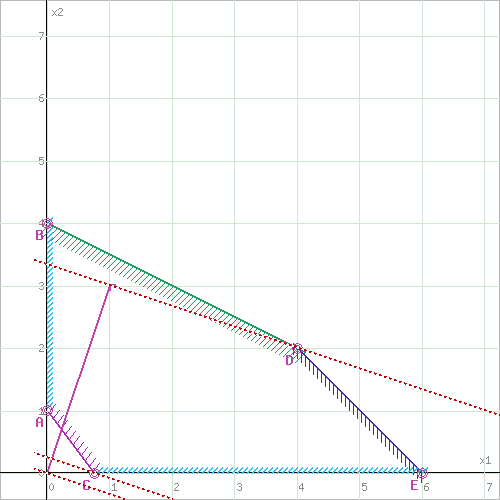 Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых: x1+3x2=8 x1+x2=6 Решив систему уравнений, получим: x1 = 0, x2 = 4 Откуда найдем максимальное значение целевой функции: F(x) = 1*0 + 2*4 = 8 F = 4x1+3x2 → min, при системе ограничений: 4x1+2x2≤8, (1) x1+3x2≤6, (2) 4x1+3x2≥4, (3) x1 ≥ 0, (4) x2 ≥ 0, (5) 1) Построим область допустимых решений, т.е. решим графически систему неравенств. 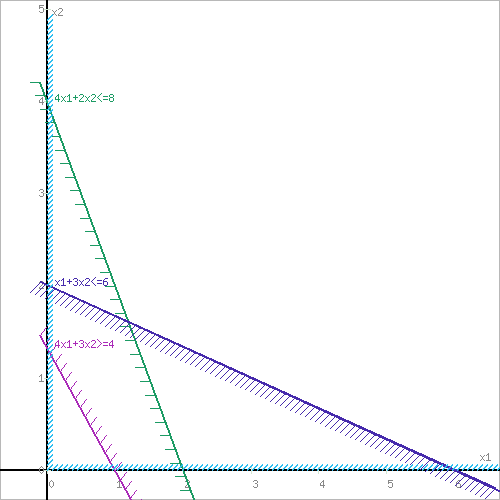 2) Границы области допустимых решений.  3. Построим прямую, отвечающую значению функции F = 4x1+3x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (4;3).  Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (3) и (4), то ее координаты удовлетворяют уравнениям этих прямых: 4x1+3x2=4 x1=0 Решив систему уравнений, получим: x1 = 0, x2 = 1.3333 Откуда найдем минимальное значение целевой функции: F(x) = 4*0 + 3*1.3333 = 4 Поскольку функция цели F(x) параллельна прямой (3), то на отрезке AC функция F(x) будет принимает одно и тоже минимальное значение. Для определения координат точки C решим систему двух линейных уравнений: x2=0 4x1+3x2=4 Решив систему уравнений, получим: x1 = 1, x2 = 0 Откуда найдем минимальное значение целевой функции: F(x) = 4*1 + 3*0 = 4 |
