Министерство образования и науки российской федерации федеральное государственное автономное образовательное учреждение высшего
 Скачать 69.4 Kb. Скачать 69.4 Kb.
|
          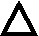          МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САМАРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА С.П. КОРОЛЁВА» (САМАРСКИЙ УНИВЕРСИТЕТ) Институт двигателей и энергетических установок Кафедра конструкции и проектирования двигателей летательных аппаратов РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА по дисциплине "Основы метода конечных элементов" Вариант 118
ЗАДАНИЕ
3 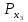 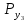 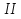 4 a=0.2м 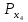 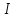 2 b=0.3м Y 1 X Рис.1 2) NZ=5 => 2;4 - закрепленные узлы. 3) Ширина а=0,1·NA=0,1·2=0,2 (м). 4) Высота b=0,1·NB=0,1·3=0,3 (м). 5) Толщина h=0,002·NH=0,002·1=0,002 (м). 6) Сосредоточенная сила - действует в положительном направлении оси y на узел 3. 7) Величина силы 5000·NF2=5000·5=25000 (Н). 8) Распределенная сила - действует в положительном направлении оси x по узлам 3 и 4. 9) Величина распределенной нагрузки 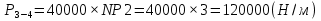 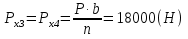 РЕФЕРАТ Пояснительная записка: 12 с,1 рисунок, 1 таблица, 1 источник. ВЕКТОРА ПЕРЕМЕЩЕНИЙ, ВЕКТОР НАГРУЗОК, МАТРИЦА ЖЕСТКОСТИ, КОНЕЧНЫЙ ЭЛЕМЕНТ, УЗЕЛ. Объектом исследования является железный параллелограмм. Цель работы : расчетное определение деформаций треугольника под действием нагрузок. В процессе работы использованы выводы из обобщенного закона Гука. В результате определены деформации в узлах треугольника и реакции опор. СодержаниеВВЕДЕНИЕ 5 1 ОСНОВНАЯ ЧАСТЬ 6 1.1 СОСТАВЛЕНИЕ ВЕКТОРА ПЕРЕМЕЩЕНИЙ И НАГРУЗОК 6 1.2 НАХОЖДЕНИЕ ПРОМЕЖУТОЧНЫХ ВЕЛИЧИН 7 1.3 СОСТАВЛЕНИЕ МАТРИЦ ЖЕСТКОСТИ 10 1.4 СОСТАВЛЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ И ИХ РЕШЕНИЕ 12 ЗАКЛЮЧЕНИЕ 14 СПИСОК ЛИТЕРАТУРЫ 15 ВВЕДЕНИЕВозникновение метода конечных элементов связано с решением задач космических исследований в 1950-х годах. Идея МКЭ была разработана в СССР ещё в 1936 году, но из-за неразвитости вычислительной техники метод не получил развития, поэтому впервые был применён на ЭВМ лишь в 1944 году Аргирисом. Этот метод возник из строительной механики и теории упругости, а уже затем было получено его математическое обоснование. Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано то, что его можно рассматривать как один из вариантов распространённого в строительной механике метода Рэлея — Ритца, который путём минимизации потенциальной энергии сводит задачу к системе линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам, описываемым уравнениями Лапласа или Пуассона. Область применения МКЭ значительно расширилась, когда было установлено (в 1968 году), что уравнения, определяющие элементы в задачах, могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как метод Галёркина или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений. 1 ОСНОВНАЯ ЧАСТЬ1.1 СОСТАВЛЕНИЕ ВЕКТОРА ПЕРЕМЕЩЕНИЙ И НАГРУЗОКВектора перемещений и нагрузок выглядят следующим образом: 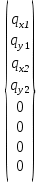 , ,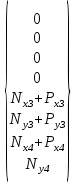 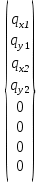 , ,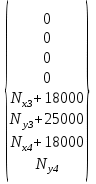 . .1.2 НАХОЖДЕНИЕ ПРОМЕЖУТОЧНЫХ ВЕЛИЧИНПлощади конечных элементов: S1=S2=0,03 (м2) Значения коэффициентов матрицы 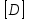 : :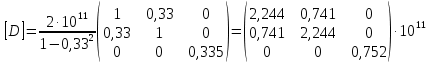 . .Координаты узлов:
Порядок узлов в конечных элементах:
Таблица 1 - Узлы элементов Матрицы 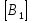 и и 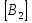 : :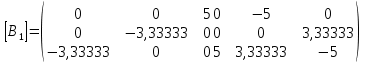 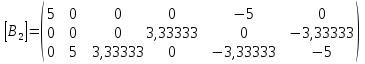 . .Транспонируем матрицы 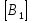 и и 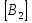 : :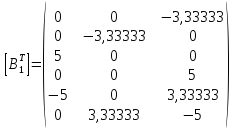 ; ;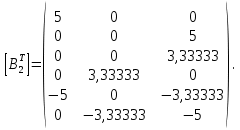 1.3 СОСТАВЛЕНИЕ МАТРИЦ ЖЕСТКОСТИМатрицы жесткости конечных элементов имеют вид: 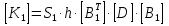 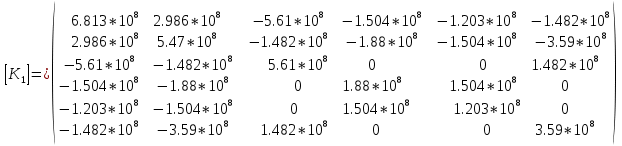   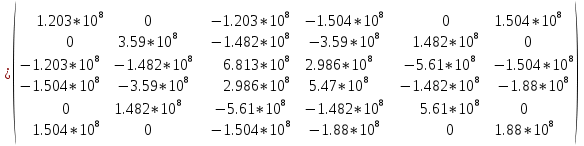 . .Общая матрица системы выглядит следующим образом: 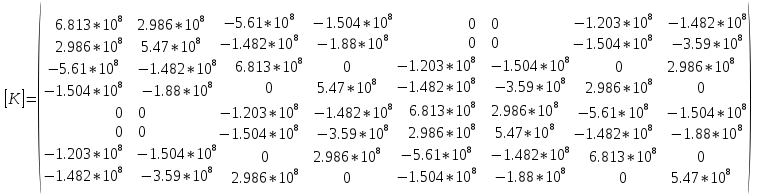 . .1.4 СОСТАВЛЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ И ИХ РЕШЕНИЕУмножим матрицу жесткости на вектор перемещений: 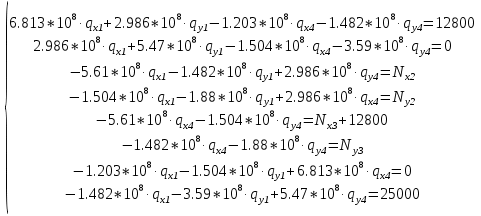 Решим часть этой системы:  Решив данную систему методом Крамера, получим: 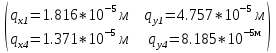 . . Найдем реакции в узлах №2 и №3: 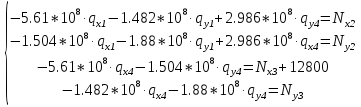 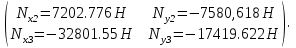 Все неизвестные определены. Задача решена. ЗАКЛЮЧЕНИЕВ результате расчетной работы определены перемещения узлов железного треугольника под действием внешних нагрузок. Определены реакции опор треугольника. СПИСОК ЛИТЕРАТУРЫ1) Уланов, А.М. Лекции по дисциплине "Основы методы конечных элементов" [Текст]. Самара 2016 |
