СРО 2. Метод конечных элементов для расчета конструкций
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
Метод конечных элементов для расчета конструкций МКЭ — аббревиатура, которая расшифровывается как "метод конечных элементов". Отсюда следует и термин "анализ МКЭ", то есть анализ и решение определенных инженерных задач с помощью данного метода. В англоязычной литературе широко распространены следующие аналоги этих аббревиатур: FEM (Finite Element Method) FEA (Finite Element Analysis) В наше время, пожалуй, сложно найти техническую сферу, в которой не применяли бы МКЭ. Вот лишь некоторые задачи, решаемые инженерами в МКЭ: механика деформируемого твердого тела (structural analysis) теплообмен (heat transfer) гидродинамика (fluid flow) массоперенос (mass transfer) электродинамика (electrodynamics) и др. 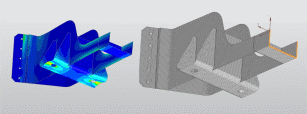 Почему МКЭ — это больше про математику, нежели про инжиниринг Не секрет, что окружающий нас мир (в целом) и инженерно-технические объекты (в частности) описываются дифференциальными уравнениями в частных производных. Как правило, получить точное аналитическое решение таких уравнений достаточно сложно, поэтому расчетчики вынуждены прибегать к численным (приближенным) методам расчета. Одним из таких инструментов и является метод конечных элементов. Суть метода конечных элементов Типовая инженерная задача в МКЭ начинается с подготовки модели — виртуального аналога реальной строительной конструкции, технологического изделия, детали механизма и т. п. С геометрической точки зрения, расчетная модель представляет собой поле точек, связанных между собой примитивами (отрезками прямых линий, треугольниками, прямоугольниками и пр.). Так образуется некая сетчатая структура — геометрия исходной конструкции аппроксимируется наложенной на нее сеткой и дальнейшая работа осуществляется уже не с исходной системой, а с полученной сеткой. Помимо геометрии, примитивы, соединяющие узловые точки модели, обладают также известными механическими свойствами. Это означает, что связав жесткости всех элементов сетки в единое целое (в рамках принятых в модели допущений), можно установить напряженно-деформированное состояние всей системы. Так расчетчик может получить любые интересующие его факторы — продольные и поперечные силы, изгибающие и крутильные моменты, напряжения, деформации и пр. Количество узлов и элементов, из которых состоит расчетная модель, заранее известно. Для некоторых сложных систем оно может измеряться тысячами и даже миллионами, но оно, так или иначе, конечно. Это обстоятельство, а также то, что заранее известен принцип "работы" каждого отдельного элемента системы, породило название — метод конечных элементов. А саму сетку называют, как правило, конечно-элементной. 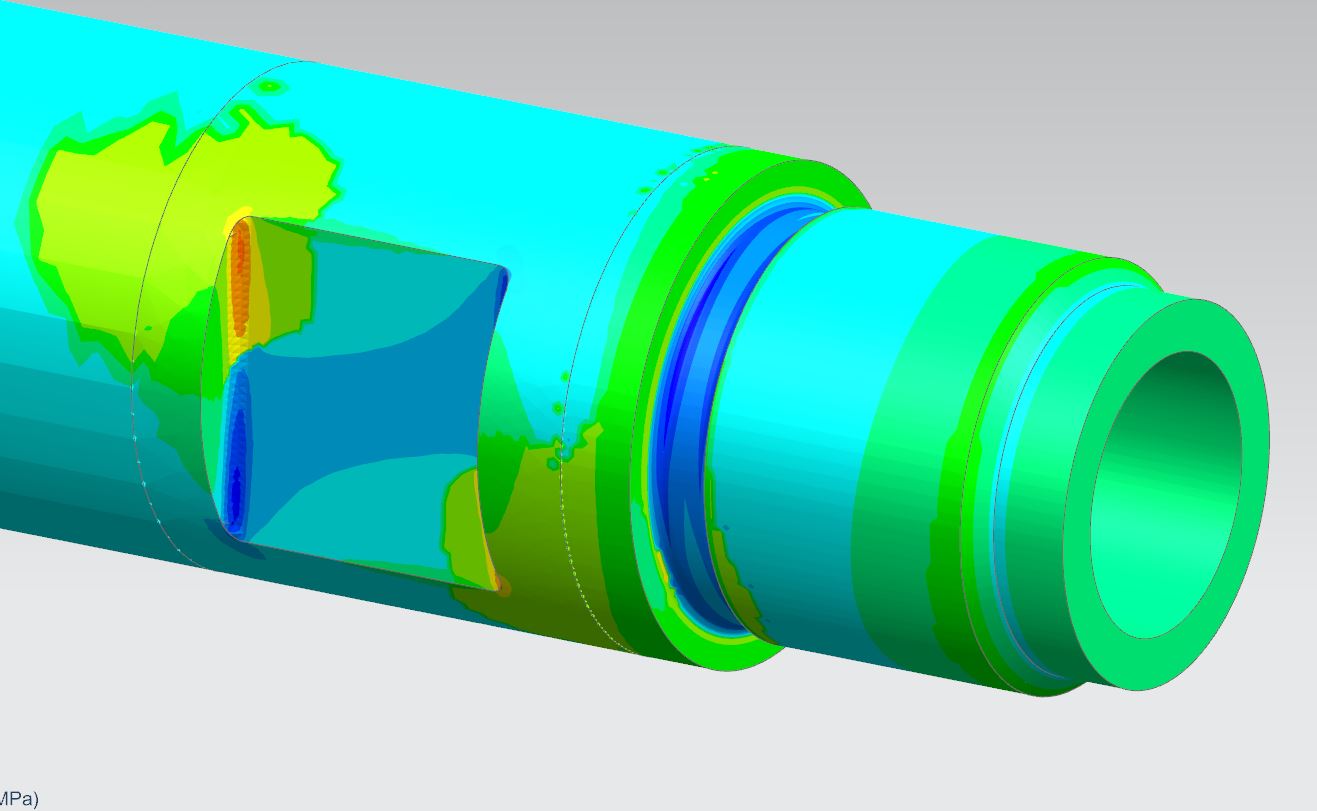 С точки зрения математики Современная интерпретация МКЭ достаточно сложна и даже беглое ее изложение выйдет за рамки этого материала. Однако, можно обозначить несколько ключевых моментов. С математической точки зрения, область, в которой ищется решение системы дифференциальных уравнений МКЭ, разделяется на подобласти (элементы) и для каждого элемента выбирается аппроксимирующая функция произвольного вида. Наиболее простой и "грубый" случай — полином первой степени: вне элемента выбранная функция равна нулю, а на границах (в узлах) функция принимает значения, которые являются решением задачи. Конечно, они заранее неизвестны. Коэффициенты полинома аппроксимирующей функции находят из условий равенства значений соседних функций в узлах. Далее составляется система линейных алгебраических уравнений, в которых число неизвестных равно числу степеней свободы системы (в общем случае, это шестикратное количество узлов сетки). Размеры сетки ограничиваются не только конкретной задачей, но и физическими возможностями компьютера (в первую очередь, размером доступной памяти). В научной и технической литературе теория метода конечных элементов излагается через матричное исчисление. Этапы, описанные выше, обязательно содержат сбор матриц жёсткости и масс конструкции. Матрица жесткости представляет собой таблицу, в которой записаны узловые реакции конечного элемента на поочередное единичное возмущение каждого его узла. Выражаясь проще, матрица жесткости конечного элемента — это система взаимосвязей всех его точек на "механическом" уровне. Зная локальную матрицу жесткости каждого отдельного элемента, компьютерная программа (CAE) формирует глобальную матрицу жесткости, суммируя жесткости всех элементов, стыкуемых в общих (смежных) узлах, с учетом их ориентации в пространстве. В итоге получается общая система взаимосвязей между всеми узлами расчетной модели. На собранные матрицы впоследствии накладываются граничные условия (т. е. учитываются закрепления системы, опоры). Инженер также задает нагрузки, моделирующие воздействие на конструкцию внешних сил, после чего полученная система линейных алгебраических уравнений решается тем или иным методом (например, весьма эффективным считается метод Холецкого). Если МКЭ реализуется в форме метода перемещений, то результатом решения являются перемещения каждого узла конструкции. По найденным узловым перемещениям могут быть найдены другие факторы напряженно-деформированного состояния. Для более глубокого понимания этих процессов рекомендуем следующие источники информации: Бате К.-Ю. Методы конечных элементов . - М.: Физматлит, 2010. - 1024 с. Зенкевич О. С. Метод конечных элементов в технике. - М.: Мир, 1975. - 543 с. Галлагер Р. Метод конечных элементов. Основы - М.: Мир,1984. - 428 с.  Программы для расчетов методом конечных элементов CAE — англоязычная аббревиатура, дословно означающая Computer-Aided Engineering. Так принято называть софт, решающий различные инженерно-технические задачи (анализ, расчёты, симуляции разнообразных физических процессов и т. п.). В подавляющем большинстве, расчётные модули современного CAE-софта основаны на численных методах решения дифференциальных уравнений, а именно МКЭ. CAE-системы почти неразрывно связаны с CAD-системами (Computer-Aided Design), поскольку оценка прочности или динамический анализ являются частью более общего цикла проектирования, конструирования изделия. Нередко они интегрированы друг в друга на уровне интерфейса пользователя. Революционное значение CAE для современной техники и инжиниринга заключается в том, что СAE-софт проверяет работоспособность изделия или конструкции без существенных затрат времени и средств на натурные испытания, так как программа на основе метода конечных элементов оценивает поведение компьютерной модели в условиях, близких к реальным. Ключевые направления CAE: FEA (Finite Element Analysis) — анализ деформаций и напряжений деталей и сборок CFD (Computer Fluid Dynamics) — вычислительная гидродинамика, анализ тепловых и жидкостных потоков MBD (MultiBody Dynamics and Kinematics) — многомассовая твердотельная динамика, кинематика Structural Optimization (оптимизация конструкций) инструменты анализа и симуляции литья, формования, штамповки и других технологических процессов Традиционно сложилось так, что разные индустрии используют разные программные решения (сам метод конечных элементов при этом, конечно, не меняется). Более того: конкурирующие компании из одной сферы стараются использовать, как правило, различные программные решения. Выбор того или иного инструмента зависит от большого количества факторов (например, круг решаемых задач, интерфейс, число пользователей, стоимость лицензии, поддержка и многое другое). В конце статьи мы дадим несколько комментариев по этому поводу. В произвольном порядке перечислим наиболее популярный CAE-софт, используемый в машиностроительной инженерии. 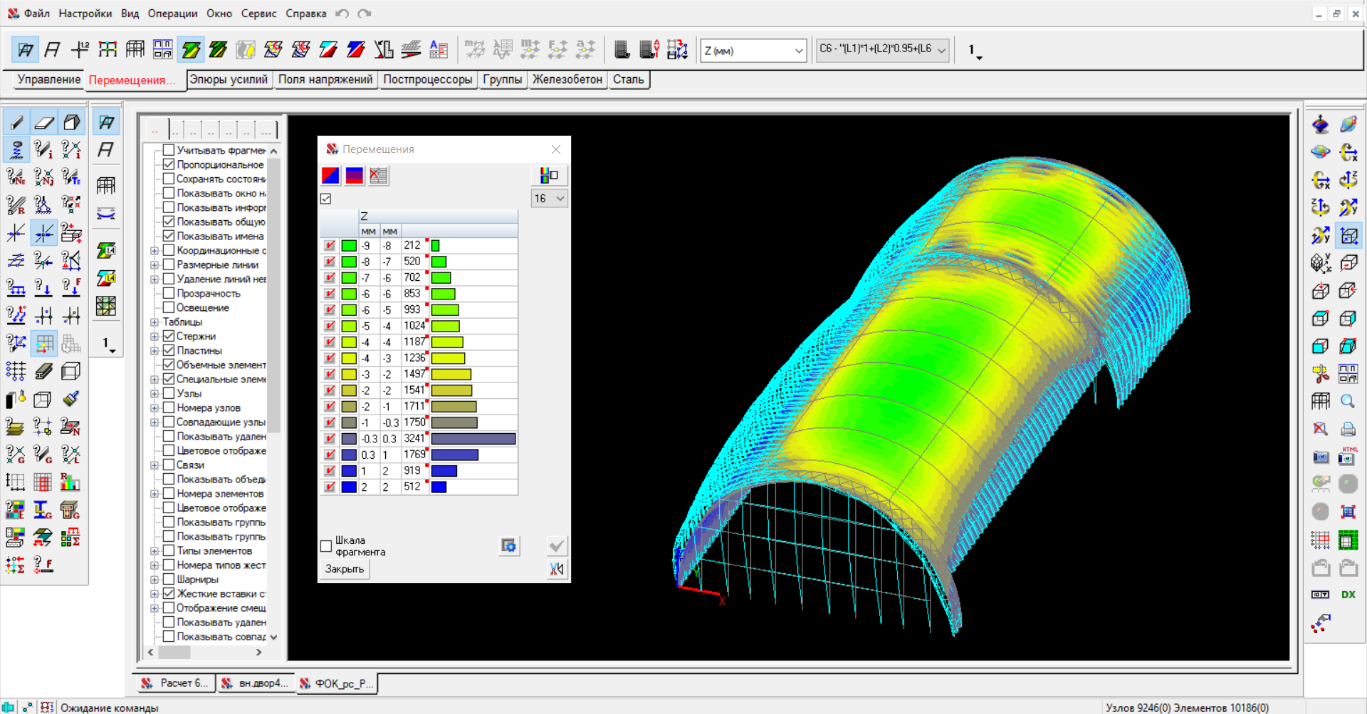 ABAQUS Программное обеспечение ABAQUS считается одним из ведущих в большой индустрии. Предлагает исключительно детальную документацию и широкий набор опций для решения. Позволяет писать субрутины "под себя" практически для всех базовых функций. Интерфейс выглядит несколько "олдскульно". Для большинства задач при работе с ABAQUS используется язык FORTRAN. ANSYS Один из наиболее старых и широко распространённых софтов в индустрии. Хорошо работает практически со всеми видами симуляций, которые встречаются в индустрии. Документация покрывает, пожалуй, до 90% возможных задач. Интерфейс ANSYS более интуитивный, чем в ABAQUS. NASTRAN NASA STRucture ANalysis. Разработан NASA и широко применяется в авиастроительной и космической индустриях. Nastran содержит публично открытый код, поэтому решатель используется во множестве других CAE-пакетов. Ориентирован, в первую очередь, на решение задач анализа конструкций. Siemens NX Представляет собой систему 3 в 1, то есть CAD + CAE + CAM. Предлагает современный интерфейс и развитые возможности, в том числе: поддержка полного цикла создания продукта, начиная от CAD (Modeling), далее переходя в CAE (Advanced Simulation) и заканчивая CAM; интерфейс, интуитивно понятный инженерам, которые имеют опыт работы в CAD-пакетах; инструменты синхронного моделирования (Synchronous Modeling), позволяющие максимально легко и быстро вносить изменения в уже существующую или импортированную модели; возможность создания "идеализированной" модели, а также ряд инструментов для подготовки модели к расчёту без затрагивания базовой геометрии; обширные возможности постпроцессора на этапе анализа и интерпретации результатов симуляций и др. SolidWorks Simulation Несмотря на то, что SolidWorks — CAD-система, ее CAE-модуль Simulation получил широкое распространение за счёт простоты использования (как решатель для относительно простых, предварительных расчётов и проверок). LS Dyna Один из первых CAE-комплексов, в котором разработчики предложили полноценный динамический анализ и опцию автоматического поиска контактных пар. 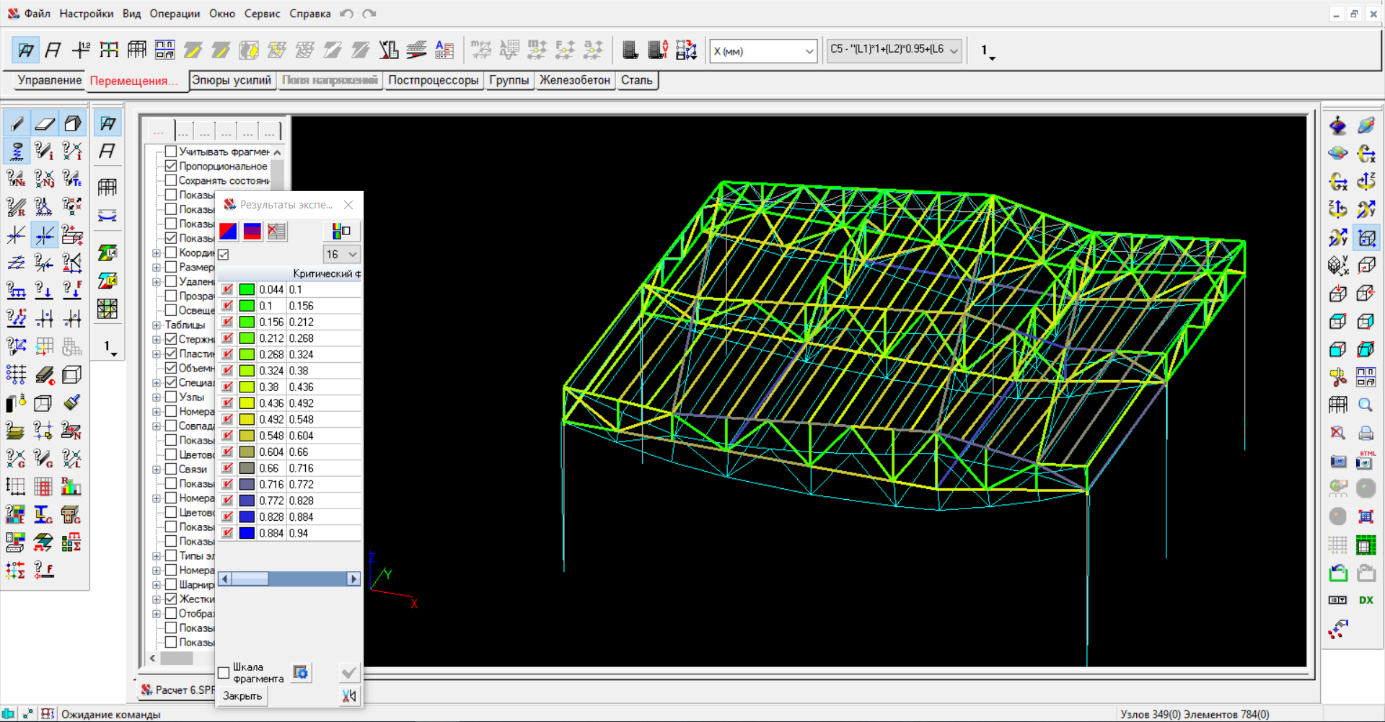 Какую программу выбрать для расчета? Как итог, дадим несколько советов по выбору программы для моделирования и симуляции. Исходите из задачи или класса задач, которые Вам предстоит решать. Поинтересуйтесь, какие для этого средства имеются в том или ином CAE-пакете. Изучите справочные материалы к программному обеспечению. Как реализована поддержка пользователей? Ведут ли разработчики официальные (неофициальные) паблики в популярных и профильных социальных сетях? Есть ли видеоканал, организуются ли вебинары или оффлайн-мероприятия, посвященные продукту? Какие плагины, надстройки, расширения актуальны для расчетного комплекса? Как комплекс интегрируется с другими программами? Можно ли импортировать, экспортировать геометрию модели из чертежных программ? Можно ли после расчета выгрузить отчет в текстовый редактор (Word, Open Office, Google Docs, TechEditor)? Перед приобретением лицензии не пренебрегайте триальными и бесплатными тестовыми версиями ПО — возможно, реальная работа с программой будет не такой, как показалось из описания или рекламного буклета. Изучите политику приобретения лицензии на программу, политику возврата средств (если она есть), а также — крайне важно — политику обновлений. Как часто выходят релизы, на какие версии Вы можете рассчитывать в обозримом будущем? Есть ли у вендора программа лояльности, что она из себя представляет? Ориентируйтесь на опыт и мнения других инженеров, но без "фанатизма". Помните, что рекомендации по выбору расчетной программы от сторонних людей не лишены субъективности и их отношение к тому или иному продукту может основываться на нюансах, которые конкретно в Вашей ситуации могут быть малозначимы. |
