основы_программирования_на_языке_python. Министерство образования и науки российской федерации федеральное государственное бюджетное образовательное учреждение высшего
 Скачать 208.8 Kb. Скачать 208.8 Kb.
|
|
Задача 25: Шашку — в дамки Ограничение по времени работы программы: 1 секунда На шахматной доске (8×8) стоит одна белая шашка. Сколькими способами она может пройти в дамки? (Белая шашка ходит по диагонали на одну клетку вверх-вправо или вверх-влево. Шашка проходит в дамки, если попадает на последнюю горизонталь.) Цвета клеток при этом не учитываются (шашка может первоначально стоять как на чёрной, так и на белой клетке). ВХОДНЫЕ ДАННЫЕ Вводятся два числа от 1 до 8: номер горизонтали и вертикали, где изначально стоит шашка. Шашке необходимо попасть на горизонталь номер 8. ВЫХОДНЫЕ ДАННЫЕ Программа должна вывести одно целое число — количество путей в дамки. ПРИМЕР
РЕШЕНИЕ Будем использовать динамическое программирование. Целевая функция - F(i,j) - количество путей шашки из начальной клетки в клетку (i,j). В клетку (i,j) можно прийти из клеток (i−1,j−1) и (i−1,j+1), поэтому F(i,j)=F(i−1,j−1)+F(i−1,j+1). Начальное значение - F(n,m)=1. В качестве ответа необходимо вывести сумму значений, записанный в 8-й строке списка, то есть sum(F[8]). Для обработки крайних клеток доски удобно ввести каемочку — столбцы с номерами 0 и 9, для которых значение функции будет равно 0. Обращение к ним будет производиться при вычислении значения функции в столбцах с номерами 1 и 8. n, m = map(int, input().split()) F = [[0] * 10 for i in range(9)] F[n][m] = 1 for i in range(n + 1, 9): for j in range(1, 9): F[i][j] = F[i - 1][j - 1] + F[i - 1][j + 1] print(sum(F[8])) Задача 26: Ход коня Ограничение по времени работы программы: 1 секунда Дана прямоугольная доска N×M (N строк и M столбцов). В левом верхнем углу находится шахматный конь, которого необходимо переместить в правый нижний угол доски. При этом конь может ходить ТОЛЬКО на две клетки вниз и на одну клетку вправо, либо на две клетки вправо и на одну клетку вниз (см. рисунок). Необходимо определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол. ВХОДНЫЕ ДАННЫЕ Программа получает на вход два натуральных числа N и M (1≤N,M≤50), записанных в одной строке. ВЫХОДНЫЕ ДАННЫЕ Выведите единственное число — количество способов добраться конём до правого нижнего угла доски. ПРИМЕР
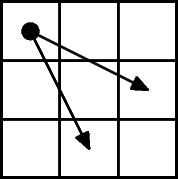 РЕШЕНИЕ Решим задачу методом динамического программирования. Целевая функция - F(i,j) - количество путей коня из начальной клетки в клетку (i,j). В клетку (i,j) можно прийти из клеток (i−1,j−2) и (i−2,j−1), поэтому F(i,j)=F(i−1,j−2)+F(i−2,j−1). Начальное значение - F(n,m)=1. В качестве ответа необходимо вывести значение F(n,m). Для обработки крайних клеток доски удобно ввести каемочку — строку и столбец с номером 0. При этом ширина каемочки должна быть две клетки, так как при вычислении значения функции приходится вычитать 2 из номера строки и номера столбца. В качестве второй строки (столбца) каемочки будет использоваться строка и столбец с номером 1 — они все заполнены нулями, кроме начальной клетки. n, m = map(int, input().split()) F = [[0] * (m + 1) for i in range(n + 1)] F[1][1] = 1 for i in range(2, n + 1): for j in range(2, m + 1): F[i][j] = F[i - 1][j - 2] + F[i - 2][j - 1] print(F[n][m]) Задача 27: Наибольшая общая подпоследовательность Ограничение по времени работы программы: 5 секунд Даны две последовательности, требуется найти длину их наибольшей общей подпоследовательности. ВХОДНЫЕ ДАННЫЕ В первой строке входных данных содержится число N – длина первой последовательности (1≤N≤1000). Во второй строке заданы члены первой последовательности (через пробел) – целые числа, не превосходящие 10000 по модулю. В третьей строке записано число M – длина второй последовательности (1≤M≤1000). В четвертой строке задаются члены второй последовательности (через пробел) – целые числа, не превосходящие 10000 по модулю. ВЫХОДНЫЕ ДАННЫЕ Требуется вывести одно число – длину наибольшей общей подпоследовательности двух данных последовательностей или 0, если такой подпоследовательности нет. ПРИМЕР
РЕШЕНИЕ Будем использовать динамическое программирование. Целевая функция - F(i,j) - длина наибольшей общей подпоследовательности для префиксов A[:i] и B[:j]. Более подробно решение задачи изложено в теоретическом материале. n = int(input()) A = input().split() m = int(input()) B = input().split() F = [[0] * (m + 1) for i in range(n + 1)] for i in range(1, n + 1): for j in range(1, m + 1): if A[i - 1] == B[j - 1]: F[i][j] = F[i - 1][j - 1] + 1 else: F[i][j] = max(F[i - 1][j], F[i][j - 1]) print(F[n][m]) Задача 28: Наибольшая общая подпоследовательность с восстановлением ответа Ограничение по времени работы программы: 5 секунд Даны две последовательности, требуется найти и вывести их наибольшую общую подпоследовательность. ВХОДНЫЕ ДАННЫЕ В первой строке входных данных содержится число N – длина первой последовательности (1≤N≤1000). Во второй строке заданы члены первой последовательности (через пробел) – целые числа, не превосходящие 10000 по модулю. В третьей строке записано число M – длина второй последовательности (1≤M≤1000). В четвертой строке задаются члены второй последовательности (через пробел) – целые числа, не превосходящие 10000 по модулю. ВЫХОДНЫЕ ДАННЫЕ Требуется вывести наибольшую общую подпоследовательность данных последовательностей, через пробел. Если таких последовательностей несколько, выведите любую из них. ПРИМЕР
РЕШЕНИЕ Сначала при помощи динамического программирования найдем длину наибольшей общей подпоследовательности, потом восстановим ответ при помощи «обратного прохода». Более подробно решение задачи изложено в теоретическом материале. n = int(input()) A = input().split() m = int(input()) B = input().split() F = [[0] * (m + 1) for i in range(n + 1)] for i in range(1, n + 1): for j in range(1, m + 1): if A[i - 1] == B[j - 1]: F[i][j] = F[i - 1][j - 1] + 1 else: F[i][j] = max(F[i - 1][j], F[i][j - 1]) Ans = [] i = n j = m while i > 0 and j > 0: if A[i - 1] == B[j - 1]: Ans.append(A[i - 1]) i -= 1 j -= 1 elif F[i - 1][j] == F[i][j]: i -= 1 else: j -= 1 print(" ".join(Ans[::-1])) Задача 29: Последовательно кратная подпоследовательность Ограничение по времени работы программы: 2 секунды Назовем последовательность «последовательнократной», если каждый ее элемент делится на предыдущий элемент. Например, 3, 6, 12 — последовательно кратная последовательность. ВХОДНЫЕ ДАННЫЕ Программа получает на вход последовательность из N натуральных чисел (N≤1000), записанных в одной строке через пробел. ВЫХОДНЫЕ ДАННЫЕ Программа должна вывести длину наибольшей последовательнократной подпоследовательности данной последовательности. ПРИМЕР
РЕШЕНИЕ Решим задачу методом динамического программирования. Целевая функция: F(i) - длина наибольшей последовательнократной подпоследовательности, заканчивающейся элементом ai. Для вычисления F(i) необходимо рассмотреть все предыдущие aj, которые являются делителями ai, и среди них выбрать такое j, что F(j) - максимально, затем взять F(i)=F(j)+1. В качестве ответа необходимо вывести наибольшее значение в списке F. A = list(map(int, input().split())) F = [0] * len(A) for i in range(len(A)): for j in range(i): if A[i] % A[j] == 0 and F[j] > F[i]: F[i] = F[j] F[i] += 1 print(max(F)) Задача 30: Наибольшая возрастающая подпоcледовательность Ограничение по времени работы программы: 2 секунды Дана последовательность целых чисел. Постройте наибольшую возрастающую подпоследовательность данной последовательности. ВХОДНЫЕ ДАННЫЕ В первой строке входных данных записано число элементов последовательности N, 1≤N≤1000. Во второй строке записаны N целых чисел через пробел. ВЫХОДНЫЕ ДАННЫЕ Требуется вывести наибольшую возрастающую подпоследовательность данной последовательности (последовательность чисел через пробел). Если таких подпоследовательностей несколько, необходимо вывести одну (любую) из них. ПРИМЕР
РЕШЕНИЕ Сначала при помощи динамического программирования найдем длину наибольшей возрастающей подпоследовательности, потом восстановим ответ при помощи «обратного прохода». Более подробно решение задачи изложено в теоретическом материале. n = int(input()) A = list(map(int, input().split())) F = [0] * len(A) for i in range(len(A)): for j in range(i): if A[i] > A[j] and F[j] > F[i]: F[i] = F[j] F[i] += 1 last = max(F) i = F.index(last) Ans = [A[i]] while F[i] != 1: j = i - 1 while F[j] != F[i] - 1 or A[j] >= A[i]: j -= 1 i = j Ans.append(A[i]) print(" ".join(map(str, Ans[::-1]))) Задача 31: k-ичные последовательности Ограничение по времени работы программы: 1 секунда По данным натуральным n и k (2≤k≤10) выведите все последовательности длины n , составленные из символов 0, … k−1, в лексикографическом порядке. ВХОДНЫЕ ДАННЫЕ Программа получает на вход два числа n и k. ВЫХОДНЫЕ ДАННЫЕ Каждая последовательность должна выводиться в отдельной строке, вывод должен завершаться символом новой строки. Числа, входящие в последовательность, должны быть разделены одним пробелом. ПРИМЕР
РЕШЕНИЕ Решим задачу при помощи рекурсивного перебора, модифицировав алгоритм построения всех двоичных последовательностей длины n. При добавлении очередного элемента нужно перебирать все числа от 0 до k−1 (включительно) в цикле. def generate(n, k, prefix): if n == 0: print(prefix) else: for next in range(k): generate(n - 1, k, prefix + str(next) + " ") n, k = map(int, input().split()) generate(n, k, "") Задача 32: Не более k единиц Ограничение по времени работы программы: 1 секунда По данным натуральным n и k (0≤k≤n) выведите в лексикографическом порядке все двоичные последовательности длины n , содержащие не более k единиц в лексикографическом порядке. ВХОДНЫЕ ДАННЫЕ Программа получает на вход два числа n и k. ВЫХОДНЫЕ ДАННЫЕ Каждая последовательность должна выводиться в отдельной строке, вывод должен завершаться символом новой строки. Числа, входящие в последовательность, должны быть разделены одним пробелом. ПРИМЕР
РЕШЕНИЕ Решим задачу при помощи рекурсивного перебора, .модифицировав алгоритм построения всех двоичных последовательностей длины n, содержащий не более k единиц. Необходимо убрать условие на добавление числа 0, так как нулей в последовательности может быть сколько угодно (есть только верхнее ограничение на число единиц). def generate(n, k, prefix): if n == 0: print(" ".join(prefix)) else: generate(n - 1, k, prefix + "0") if k > 0: generate(n - 1, k - 1, prefix + "1") n, k = map(int, input().split()) generate(n, k, "") Задача 33: Сумма кубов Ограничение по времени работы программы: 2 секунды Дано натуральное число N. Необходимо представить его в виде суммы точных кубов натуральных чисел, содержащей наименьшее число слагаемых. Программа должна вывести это число слагаемых. ВХОДНЫЕ ДАННЫЕ Программа получает на вход натуральное число N, не превосходящее 104. ВЫХОДНЫЕ ДАННЫЕ Программа должна вывести единственное натуральное число - минимальное число слагаемых в представлении N в виде суммы точных кубов. ПРИМЕР
Примечание. 33=23+23+23+23+13. РЕШЕНИЕ Решим задачу методом динамического программирования. Целевая функция: F(n) - минимальное число слагаемых в представлении числа n в виде суммы кубов. Далее рассмотрим одно возможное слагаемое, если оно равно j3, то нужно выбрать такое j, для которого F(n−j3) - минимально. Рекуррентное соотношение - F(n)=1+minjF(n−j3), где нужно брать такие j, что j3≥n. Начальное значение F(0)=0. N = int(input()) INF = 10 ** 10 F = [0] * (N + 1) for i in range(1, N + 1): F[i] = F[i - 1] + 1 j = 2 while j ** 3 <= i: if F[i - j ** 3] < F[i]: F[i] = F[i - j ** 3] + 1 j += 1 print(F[N]) Задача 34: Банкомат Ограничение по времени работы программы: 1 секунда В некотором государстве в обращении находятся банкноты определенных номиналов. Национальный банк хочет, чтобы банкомат выдавал любую запрошенную сумму при помощи минимального числа банкнот, считая, что запас банкнот каждого номинала неограничен. Помогите Национальному банку решить эту задачу. ВХОДНЫЕ ДАННЫЕ Первая строка входных данных содержит натуральное число N не превосходящее 100 — количество номиналов банкнот в обращении. Вторая строка входных данных содержит N различных натуральных чисел x1, x2, …, xN, не превосходящих 105 — номиналы банкнот. Третья строчка содержит натуральное число S, не превосходящее 105 —сумму, которую необходимо выдать. ВЫХОДНЫЕ ДАННЫЕ Программа должна найти представление числа S в виде суммы слагаемых из множества xi, содержащее минимальное число слагаемых и вывести это представление на экран (в виде последовательности чисел, разделенных пробелами). Если таких представлений существует несколько, то программа должна вывести любое (одно) из них. Если такого представления не существует, то программа должна вывести строку «No solution». ПРИМЕР
РЕШЕНИЕ Данная задача почти полностью была разобрана на занятии. Единственное отличие - необходимость вывести «No solution», если значение F(N)≥+∞, во всех остальных случаях необходимо восстановить ответ и вывести восстановленный ответ. N = int(input()) A = list(map(int, input().split())) N = int(input()) INF = 10 ** 10 F = [INF] * (N + 1) F[0] = 0 Prev = [0] * (N + 1) for k in range(1, N + 1): for i in range(len(A)): if k - A[i] >= 0 and F[k - A[i]] < F[k]: F[k] = F[k - A[i]] Prev[k] = A[i] F[k] += 1 if F[N] >= INF: print("No solution") else: while N > 0: print(Prev[N], end=' ') N -= Prev[N] |
