лаба дм. Міністерство освіти та науки україни харківський національний університет радіоелектроніки
 Скачать 65.98 Kb. Скачать 65.98 Kb.
|
|
МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ Кафедра інформаційних управляючих систем (ІУС) Звіт з виконання лабораторної роботи №4 ««НАЙКОРОТШІ ШЛЯХИ. АЛГОРИТМ ДЕЙКСТРИ»» З дисципліни «Дискретна математика»
Харків 2019
Ознайомлення з основними методами та алгоритмами розв’язання задач відшукання оптимальних шляхів в орієнтованих графах (алгоритмами Дейкстри, Форда, Флойда, Данцига). Вивчення формального опису алгоритму Дейкстри побудови найкоротших шляхів із вершини графа. Програмна реалізація алгоритму Дейкстри для знаходження відстані між парами вершин в орієнтованих і неорієнтованих графах.
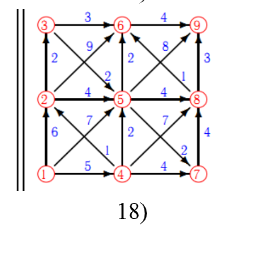
#include #include #include #include #include using namespace std; char NEWT[256]; char*RUS(char*TEXT) { CharToOem(TEXT,NEWT); return NEWT;} int v; int main() { int massdop[4]; fstream Out ; Out.open("C:\\Users\\OWN\\Desktop\\gg.txt",ios::in); int i,j; int infinity=1000; // Бесконечность // Количество вершин в графе int VES[100][100]; // Матрица весов графа int x[100]; //Массив, содержащий единицы и нули для каждой вершины, // x[i]=0 - еще не найден кратчайший путь в i-ю вершину, // x[i]=1 - кратчайший путь в i-ю вершину уже найден int DlinaPuti[100]; //t[i] - длина кратчайшего пути от вершины s в i int PredVertex[100]; //h[i] - вершина, предшествующая i-й вершине //на кратчайшем пути int VERTEX; int p; cout< cin>>VERTEX;p= VERTEX; //Число вершин в графе //cout< //cout< for (i=0;i //cout< //cout< for(i=0;i {//cout< for(j=0;j Out>>VES[j][i];} // Будем искать путь из вершины s в вершину g по циклу int start; // Номер исходной вершины int end; // Номер конечной вершины N: cout< cin>>start; if (start>(p-1) && start<0) {cout< start=start-1; //так как массив начинается с 0 отнимаем от вводимой цифры 1 for (int prosto=0;prosto {end=prosto; //цикл прогоняет алгоритм Флойда p-ое количество раз преврашая его в алгоритм Дейкстры if (end==start) continue; //исключаем просчет растояния между одной и той же точкой else { // Инициализируем начальные значения массивов int u; // Счетчик вершин for (u=0;u { DlinaPuti[u]=infinity; //Сначала все кратчайшие пути из s в i //равны бесконечности x[u]=0; // и нет кратчайшего пути ни для одной вершины } PredVertex[start]=0; // s - начало пути, поэтому этой вершине ничего не предшествует DlinaPuti[start]=0; // Кратчайший путь из s в s равен 0 x[start]=1; // Для вершины s найден кратчайший путь v=start; // Делаем s текущей вершиной while(1) { // Перебираем все вершины, смежные v, и ищем для них кратчайший путь for(u=0;u { if(VES[v][u]==0)continue; // Вершины u и v несмежные if(x[u]==0 && DlinaPuti[u]>DlinaPuti[v]+VES[v][u]) //Если для вершины 'u' еще не //найден кратчайший путь // и новый путь в 'u' короче чем //старый, то { DlinaPuti[u]=DlinaPuti[v]+VES[v][u]; //запоминаем более короткую длину пути в //массив t[и] PredVertex[u]=v; //запоминаем, что v->u часть кратчайшего //пути из s->u } } // Ищем из всех длин некратчайших путей самый короткий int w=infinity; // Для поиска самого короткого пути v=-1; // В конце поиска v - вершина, в которую будет // найден новый кратчайший путь. Она станет // текущей вершиной for(u=0;u { if(x[u]==0 && DlinaPuti[u] // путь и если длина пути в вершину 'u' меньше // уже найденной, то { v=u; // текущей вершиной становится 'u'-я вершина w= DlinaPuti[u]; } } if(v==-1) { cout< break; } if(v==end) // Найден кратчайший путь, { // выводим его cout< u=end; int i=0; while(u!=start) {i++; cout<<" "< u=PredVertex[u]; } cout<<" "< break; } x[v]=1; }}} return 0;}  1.4. Результат програми 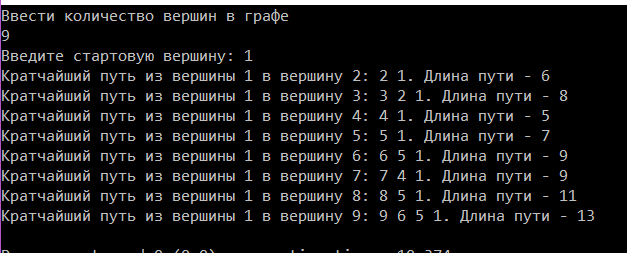 1.5. Висновки. Було ознайомлено з основними методами та алгоритмами розв’язання задач відшукання оптимальних шляхів в орієнтованих графах (алгоритмами Дейкстри, Форда, Флойда, Данцига). Вивчено формальний опис алгоритма Дейкстри побудови найкоротших шляхів із вершини графа.Була підготовлена програмна реалізація алгоритму Дейкстри для знаходження відстані між парами вершин в орієнтованих і неорієнтованих графах. |
