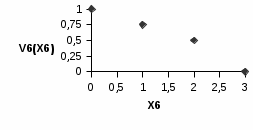Метод Кини-Райфа. Задание_на_практику_Аксиоматический_метод_Кини_Райфа. Многокритериальные методы принятия решений. Метод КиниРайфа

• Название: Многокритериальные методы принятия решений. Метод КиниРайфа
• Анкор: Метод Кини-Райфа
• Дата: 23.12.2021
• Размер: 196.79 Kb.
• Имя файла: Задание_на_практику_Аксиоматический_метод_Кини_Райфа.docx
• Тип: Документы; #315281

Многокритериальные методы принятия решений. Метод Кини-Райфа.

Для оценки риска при страховании автомобилей страховая компания использует индивидуальные характеристики транспортного средства (ТС) и водителей, допущенных к управлению:

1. 
   Возраст младшего водителя (при наличии нескольких водителей), число целых лет.
   
2. 
   Стаж вождения наименее опытного водителя (при наличии нескольких водителей), число целых лет.
   
3. 
   Количество водителей, допущенных к управлению транспортным средством.
   
4. 
   Возраст транспортного средства, число целых лет.
   
5. 
   Действительная стоимость транспортного средства на момент оценки риска, тыс. рублей.
   
6. 
   Цвет транспортного средства. Предлагается использовать 4 группы цветов: светлые тона не «металлик» (белые, бежевые), цветные не «металлик», темные (черные, синие, темно-зеленые) не «металлик», а также любые цвета с названиями, включающими слова «металлик», серебристые, золотистые.
   
7. 
   Отсутствие требований выплат (безаварийная эксплуатация), в качестве значений данного фактора предлагается использовать количество лет безаварийной эксплуатации транспортного средства.
   

Построить многомерную функцию для оценки риска при страховании по методу Кини-Райфа.

v(x₁, x₂, …, x_K) = ,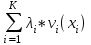

где значения v(x₁,x₂,..x_K) и v_i(x_i), i=1,2,..K меняются от нуля до единицы;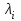

- шкалирующий коэффициент при одномерной функции ценности v_i(x_i), такой что 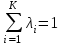, 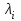>0.

Найти значение функции для профиля по вариантам.

Вариант 1	(25 лет водителю; стаж 2 года; 0 доп. водителей; 7 лет ТС; стоимость 570 тыс. руб.; цвет «белый»; 0 лет безубыточной эксплуатации)
Вариант 2	(55 лет водителю; стаж 7 года; 1 доп. водитель; 3 года ТС; стоимость 720 тыс. руб.; цвет «красный»; 4 года безубыточной эксплуатации)
Вариант 3	(18 лет водителю; стаж 0 лет; 1 доп. водителей; 1 год ТС; стоимость 400 тыс. руб.; цвет «белый»; 0 лет безубыточной эксплуатации)
Вариант 4	(34 года водителю; стаж 3 года; 0 доп. водителей; 2 года ТС; стоимость 790 тыс. руб.; цвет «черный»; 1 год безубыточной эксплуатации)
Вариант 5	(40 лет водителю; стаж 5 лет; 1 доп. водитель; 3 года ТС; стоимость 650 тыс. руб.; цвет «белый»; 0 лет безубыточной эксплуатации)
Вариант 6	(58 лет водителю; стаж 20 лет; 1 доп. водителей; 15 лет ТС; стоимость 970 тыс. руб.; цвет «черный»; 5 лет безубыточной эксплуатации)
Вариант 7	(43 года водителю; стаж 2 года; 0 доп. водителей; 5 лет ТС; стоимость 990 тыс. руб.; цвет «белый»; 5 лет безубыточной эксплуатации)
Вариант 8	(28 лет водителю; стаж 8 лет; 0 доп. водителей; 5 лет ТС; стоимость 1000 тыс. руб.; цвет «черный»; 0 лет безубыточной эксплуатации)
Вариант 9	(25 лет водителю; стаж 5 лет; 1 доп. водитель; 10 лет ТС; стоимость 850 тыс. руб.; цвет «металлик»; 0 лет безубыточной эксплуатации)
Вариант 10	(30 лет водителю; стаж 3 года; 2 доп. водителя; 5 лет ТС; стоимость 900 тыс. руб.; цвет «белый»; 0 лет безубыточной эксплуатации)

Алгоритм нахождения многомерной функции ценности

1. 
   Для каждого критерия i, i=1,2,..K определить наилучшее b_i и наихудшее w_i возможные значения.
   
2. 
   Проранжировать шкалирующие коэффициенты _i по степени влияния соответствующих факторов на ожидаемый размер ущерба.
   
3. 
   Для каждого критерия i, i=1,2,..K построить одномерную функцию ценности v_i(x_i).
   
4. 
   Определить шкалирующие коэффициенты _i критериевi, i=1,2,..K.
   
5. 
   Построить многомерную функцию ценности.
   
6. 
   Получив вид аддитивной функции v(x₁, x₂, …, x_K), для каждого объекта, принимаемого на страхование, вычислить значение данной функции.
   

Исходные данные

По оценкам экспертов были получены крайние значения критериев и занесены в таблицу 2.

Таблица 2

Наилучшие b_i и наихудшие w_i значения критериев

Номер (i) критерия	1	2	3	4	5	6	7
Наиме-нование	Возраст водителя	Стаж водителя	Число доп.вод.	Возраст ТС	Действ. ст-сть ТС	Цвет ТС	Кол-во лет безаварийной экс-ции
bi	30 - 50	60	0	0	20	светлый	4
wi	18; 80	0	4	20	1000	металлик	0

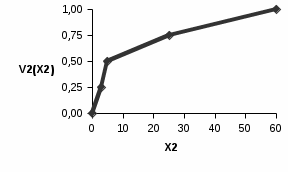
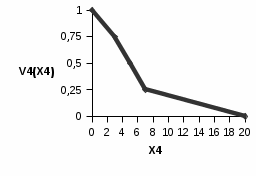
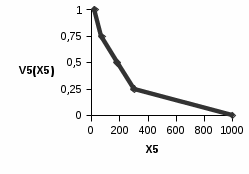
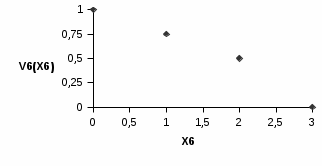
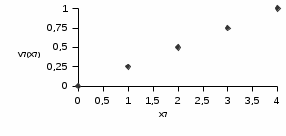
Эксперты проранжировали критерии по уровню значимости следующим образом:

₄ >₅ >₂ >₁ >₇ >₆ >₃ , то есть наиболее важным при оценке ожидаемого размера ущерба оказался возраст транспортного средства, наименее значимым – число дополнительных водителей (помимо основного), допущенных к управлению автомобилем.

О 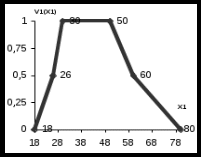дномерные функции ценности

1. Возраст водителя	2. Стаж
3. Число дополнительных водителей	4. Возраст транспортного средства
5. Действительная стоимость транспортного средства	6. Цвет транспортного средства
7. Количество лет безаварийной эксплуатации автомобиля

При сравнении профилей были получены следующие выражения ₁, ₂, ₃, ₅, ₆, ₇ через ₄:

₅ = 0,92₄ ; ₂ = 0,83₄ ; ₁ = 0,75₄ ; ₇ = 0,625₄ ; ₆ = 0,5₄ ; ₃ = 0,375₄