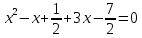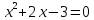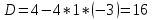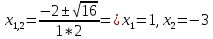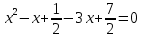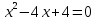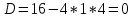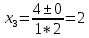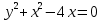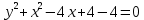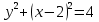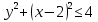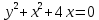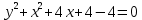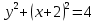Множества Алгебра и геометрия. ДымкоАндрейКИ18-06бМножества. "Множества"

• Название: "Множества"
• Анкор: Множества Алгебра и геометрия
• Дата: 09.05.2022
• Размер: 168.3 Kb.
• Имя файла: ДымкоАндрейКИ18-06бМножества.docx
• Тип: Документы; #518979

Федеральное государственное автономное

образовательное учреждение

высшего образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Институт Космических и Информационных Технологий

Кафедра вычислительной техники

РАСЧЕТНОЕ ЗАДАНИЕ

Индивидуальные задания по теме "Множества"

Вариант 7

Студент КИ18-06б 031831238 _____________ Дымко А.С.

Красноярск 2019

Задание 1.

Для универсального множества U = {-5, -4, -3, -2, -1, 1, 2, 3, 4, 5}, множества A = {-3, -1, 1, 2}, и для B, являющегося множеством корней уравнения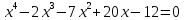

:

1. 
   Найти множества .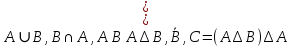
   
2. 
   Выяснить какая из возможностей 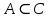, или 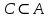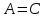, или , или 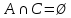выполнена для множеств A и С.
   
3. 
   Найти P(B) и |P(B)|.
   

Решение:

Для нахождения элементов множества B нам необходимо решить уравнение 4-ой степени вида 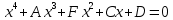. Для этого воспользуемся методом Феррари. Нам потребуется один из корней уравнения y₀.

Т.к. для реализации метода нам требуется лишь 1 корень уравнения и уравнение не имеет дробных коэффициентов, то мы можем найти его самым простым способом – подбором. При х = 1 мы будем иметь 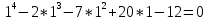, т.е. 0 = 0, т.е. x = 1 = y₀ является корнем уравнения.

Запишем два квадратных уравнения по формуле: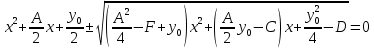



Подставим значения A = -2, F = -7, C = 20, D = -12, y₀ = 1: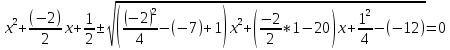



Упростим: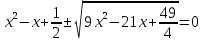



Рассмотрим выражение под корнем и соберем его при помощи формулы квадрата разности: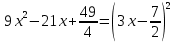



Подставим получившееся выражение, извлечем корень, получим два квадратных уравнения, решим их:

Уравнение имеет один корень

Множество B = {-3, 1, 2}

№1.1

A = {-3, -1, 1, 2}

B = {-3, 1, 2}

U = {-5, -4, -3, -2, -1, 1, 2, 3, 4, 5}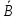

1. 
   A∪B = {-3, -1, 1, 2}
   
2. 
   B∩A = {-3, 1, 2}
   
3. 
   A\B = {-1}
   
4. 
   B\A = ∅
   
5. 
   A∆B = {-1}
   
6. 
   = {-5, -4, -2, -1, 3, 4, 5}
   
7. 
   C = (A∆B)∆A = ∅
   

№1.2

Т.к. -3∉С, и -1∉C, и 2∉C, то A∩C= ∅ – выполняется для множеств A и C.

№1.3

P(B) – булеан.

P(B) = {{∅}, {-3}, {1}, {2}, {-3, 1}, {-3, 2}, {1, 2}, {-3, 1, 2}}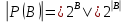

, т.к. |B| = 3, то |P(B)| = 2³ = 8

Задание 2.

Пусть A, B и C – множества точек плоскости, координаты которых удовлетворяют условиям: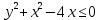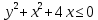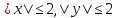

1. 
   
   
2. 
   
   
3. 
   
   

Изобразите в системе координат x0yмножество D, полученное из множеств A, B и C по формуле .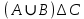

Упростим выражения:

Применим формулу квадрата разности: Это уравнение окружности с центром в точке (2, 0) и радиусом 2.

Применим формулу квадрата суммы: Это уравнение окружности с центром в точке (-2, 0) и радиусом 2.

Изобразим эти окружности, а затем выберем области, которые удовлетворяют условиям A и B. Объединение этих областей является частью искомой области (A∪B).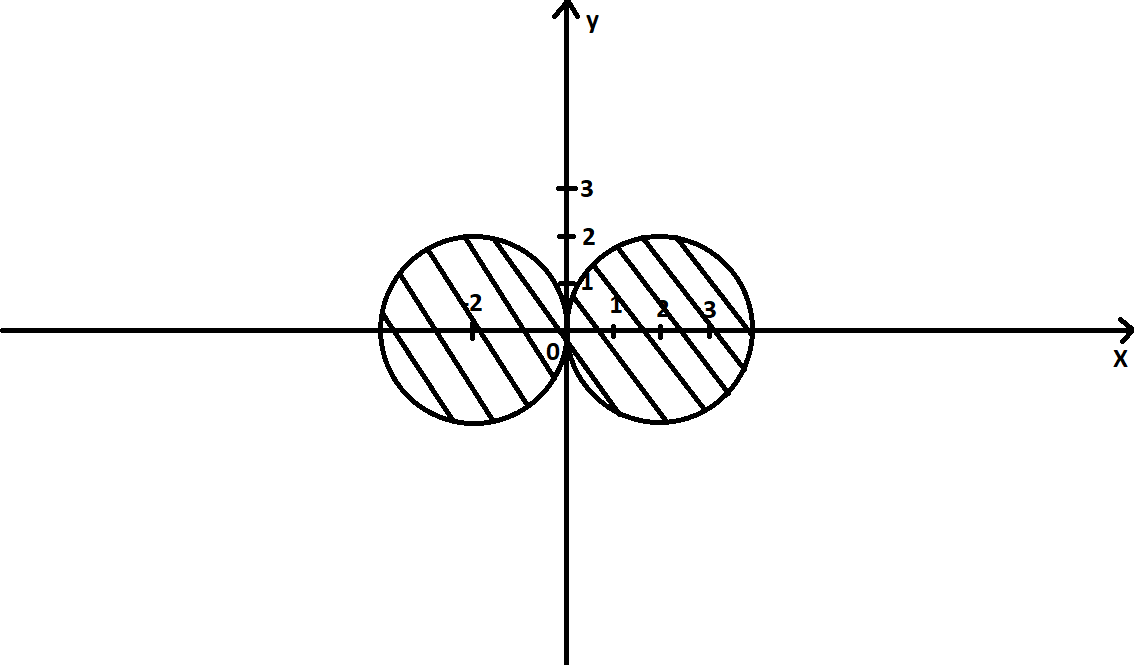



Изобразим область, удовлетворяющую условию C: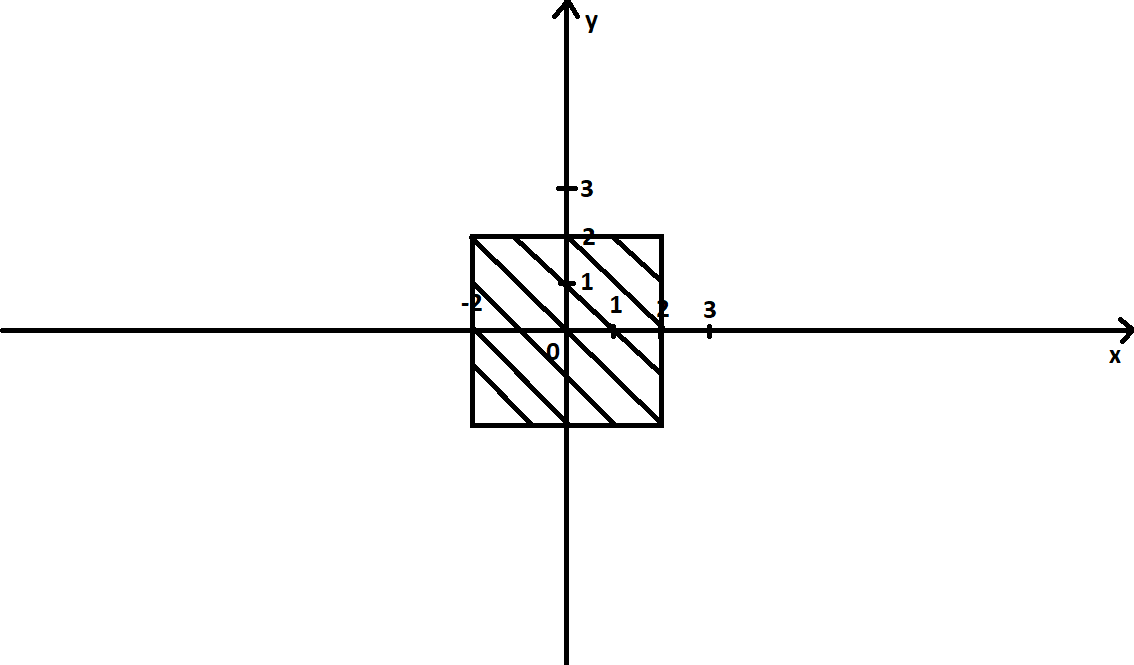



Теперь объединим эти области по правилу (A∪B)∆C. Область, заштрихованная красным – искомая.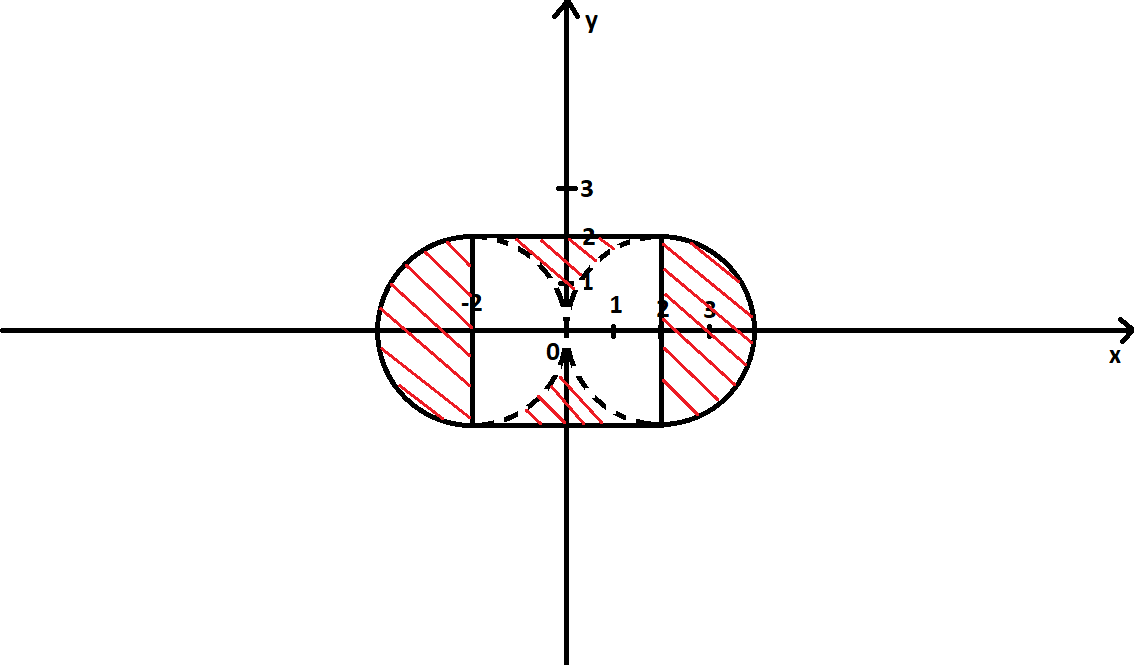



Задание 3.

Решить систему уравнений относительно множества X и указать условия совместности системы.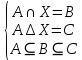



Решение:

Составим диаграмму Венна по третьему условию системы: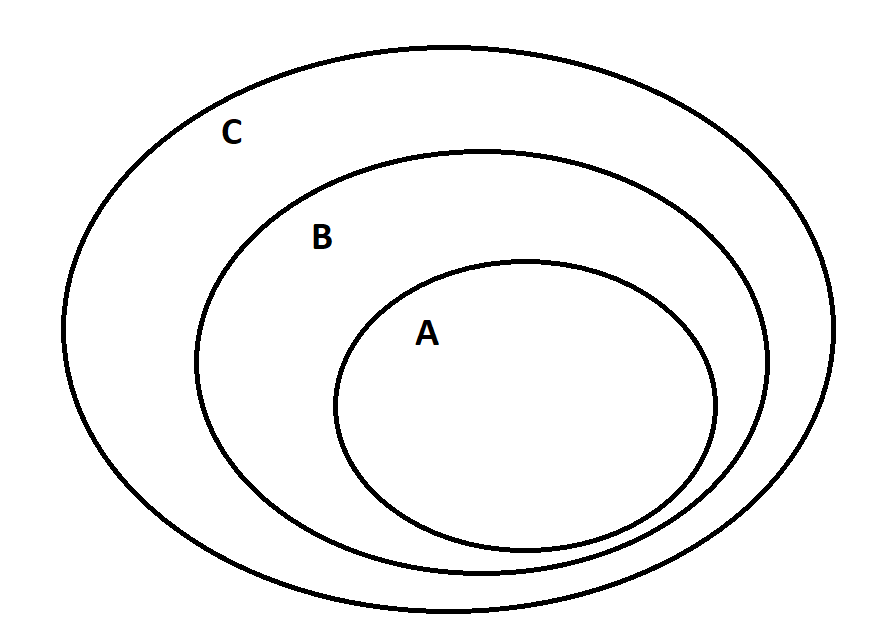



Модифицируем ее, учитывая первое условие системы: Если все элементы множества, принадлежащие одновременно X и A, дают множество B, то A = B и A = B ⊆X.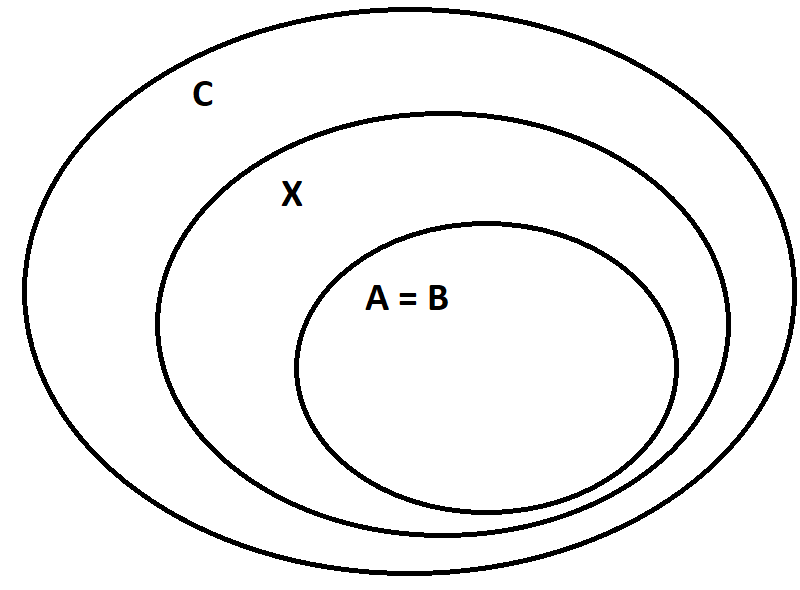



Затем рассмотрим второе условие системы: С = A ∆ X = (A\X) ∪ (X\A). В частности, нас интересуют выражения в скобках.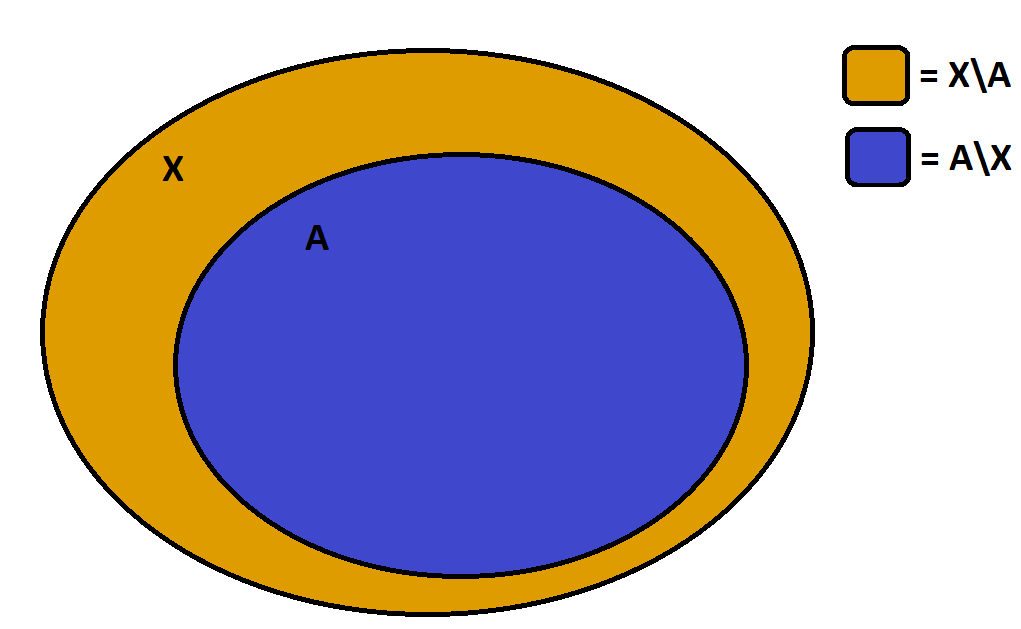



А т.к. объединение этих двух множеств дает множество C по условию, то X = C.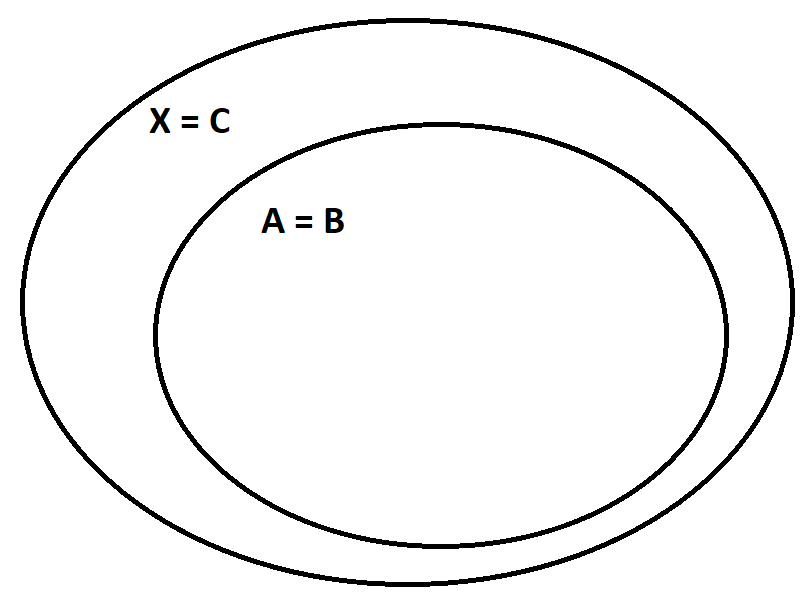



Ответ: X = C, условия совместности системы: A = B ⊆ С.