Нелинейные регрессии, Эксперт построения моделей. Модель Нелинейные модели Нелинейный мнк
 Скачать 1.45 Mb.
|
|
Предсказанные значения показаны в следующей таблице в виде переменной с именем PRED.
Способ 2. Использование нелинейной регрессии. Воспользуемся статистическим пакетом SPSS, в котором реализован метод непосредственного определения параметров нелинейной регрессии. После запуска программы SPSS в редакторе данных вставляем исходные данные, скопированные из Excel. Присваиваем имя переменным, указываем тип, ширину, и метки  Выберем в верхней строке меню Анализ →Регрессия →Нелинейная. Поместим переменную «Объем производства» в поле для зависимых переменных и введем выражение, задающую модель 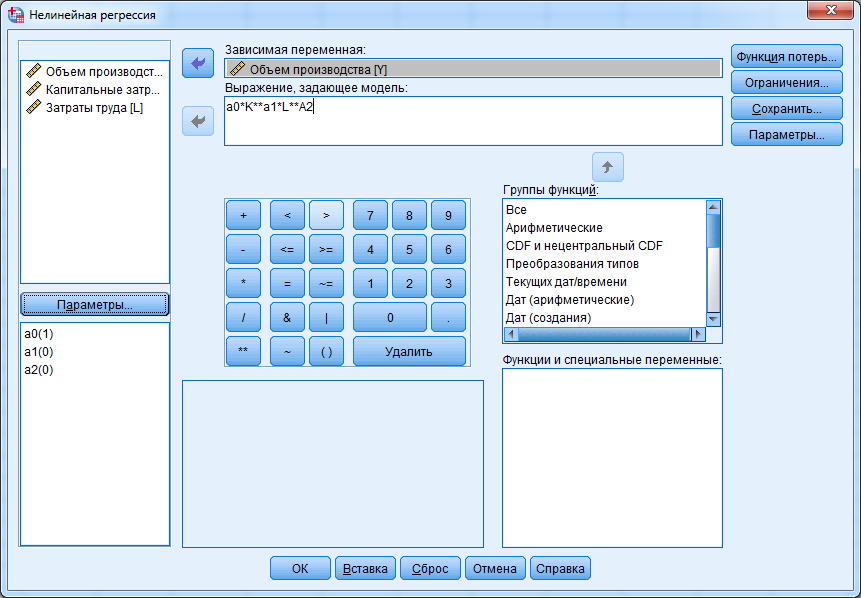 Щелкнем по кнопке Параметры в левой части окна. Получим диалоговое окно, в котором можно задавать начальные значения параметров модели  Щёлкнем на кнопке Сохранить и отметим нужные типы сохраняемых факторов (Предсказанные значения).  При этом в исходных данных появится новая переменная PRED, которая содержит вычисленные (предсказанные) значения объема производства.
В следующей таблице приводятся оценки параметров модели вместе с соответствующей стандартной ошибкой и доверительным интервалом
Получили следующую производственную функцию с коэффициентами, немного отличающимися от полученных ранее 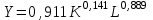 .Модель, полученная способом 2, лучше аппроксимирует исходные данные (по алгоритму в модели 2 минимизируется отклонение модели от исходных данных, а не от их логарифмов) ▲ Решим пример 6.2 нелинейным МНК. ▼ На рис. 6.12 представлено основное окно с переменными. Оценим параметры модели нелинейной регрессии, воспользовавшись командой Модель – Нелинейные модели – Нелинейный МНК. В открывшемся окне «нелинейный МНК» введите строки, как показано на рис. 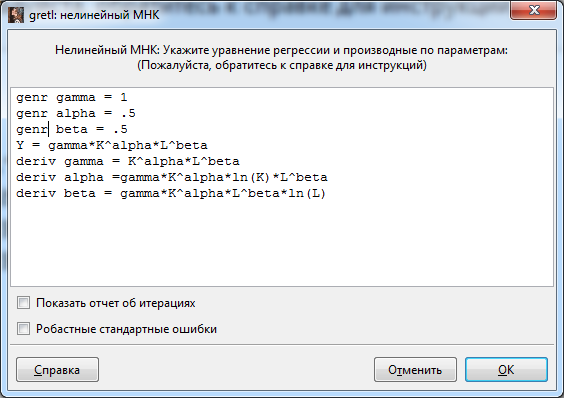 Рис. Заполненное диалоговое окно: нелинейный МНК Здесь в первых трех строках «genr» указаны начальные значения параметров модели: alpha, beta и gamma. Следующая строка определяет функцию регрессии, а последние три строки «deriv» предоставляют производные этой функции относительно каждого из параметров по очереди. Результаты оценки уравнения регрессии методом нелинейного МНК представлены на рис. 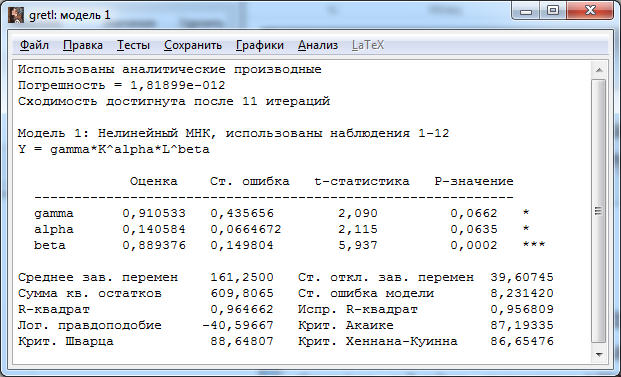 Рис. Результаты оценивания параметров модели Получили следующую производственную функцию 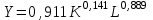Расчетные и наблюдаемые значения для данной зависимости представлены в табл. и на графике рис. . Табл. 7.2 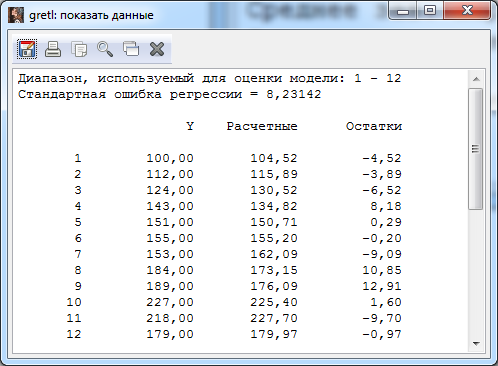 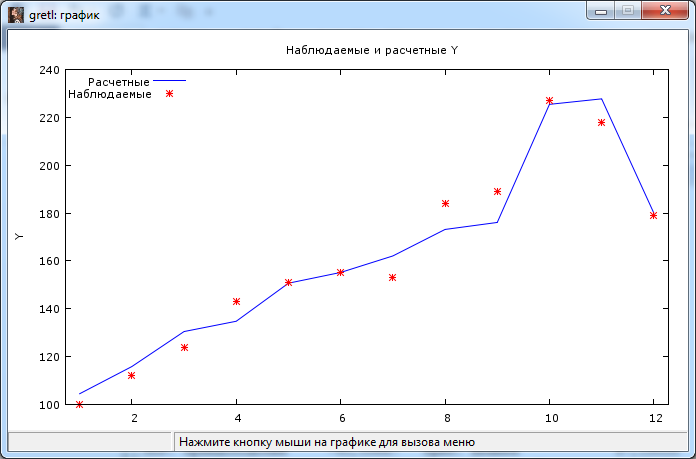 Рис. График наблюдаемых и расчетных значений ▲ Эксперт построения моделейвременного ряда в программе SPSS Сезонная модель представляется в виде: ARIMA(р, d, q)(P, D, Q)s, где к параметрам модели р, d, q добавлены сезонные параметры P, D, Q и s — сезонная авторегрессия, сезонная разность, сезонное скользящее среднее и сезонный период соответственно. Идентификация сезонной модели производится тем же способом, что и идентификация несезонной модели. Поведение автокорреляционной и частной автокорреляционной функций на начальных лагах позволяет идентифицировать стандартным образом несезонную компоненту, а на лагах, кратных сезонному лагу — сезонную составляющую. При наличии ярко выраженной сезонной компоненты целесообразно включение в модель сезонного дифференцирования, но при этом желательно, чтобы d + D 2. Наиболее подходящая модель ARIMA(р, d, q)(P, D, Q)s выбирается путем отбора моделей, параметры которых принимают следующие возможные значения: p, d, q = 0, 1, 2; Ps, Ds, Qs = 0, 1. Существенно облегчить решение задач анализа и прогнозирования финансово-экономических показателей поможет использование современных компьютерных статистических пакетов. В некоторых компьютерных пакетах реализованы процедуры автоматического подбора структуры модели Бокса — Дженкинса (АРПСС). Процедура построения моделей временного ряда в программе SPSS включает в себя инструмент Эксперт построения моделей, который автоматически идентифицирует и оценивает наиболее подходящую модель Бокса — Дженкинса или экспоненциального сглаживания, исключая необходимость определения подходящей модели методом проб и ошибок. Пример. Используя пакет SPSS, проведем подбор ARIMA-модели по данным пассажирских авиаперевозок  одной из авиакомпаний (тыс. чел.) за 2010-2015 гг. и сделаем прогноз на следующий 2016 год.Исходные данные
▼ Укажем последовательность действий. • Вводим данные примера в таблицу в один столбец с именем «Авиаперевозки» (рис. 1). 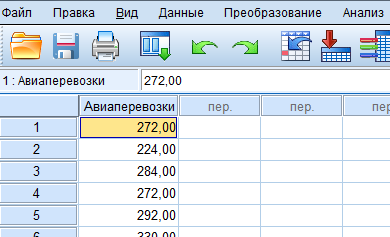 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||