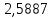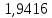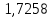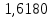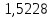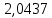15 лаба по физике 2 сем. Лаба 15. Моделирование магнитного поля токов
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра Физики отчет по лабораторной работе №15 по дисциплине «Физика» Тема: Моделирование магнитного поля токов
Санкт-Петербург 2021 Цель работы. Изучение магнитного поля системы проводников с использованием графической карты поля, полученной методом моделирования; расчет индуктивности системы проводников заданной конфигурации. Основные теоретические положения. Схема установки В 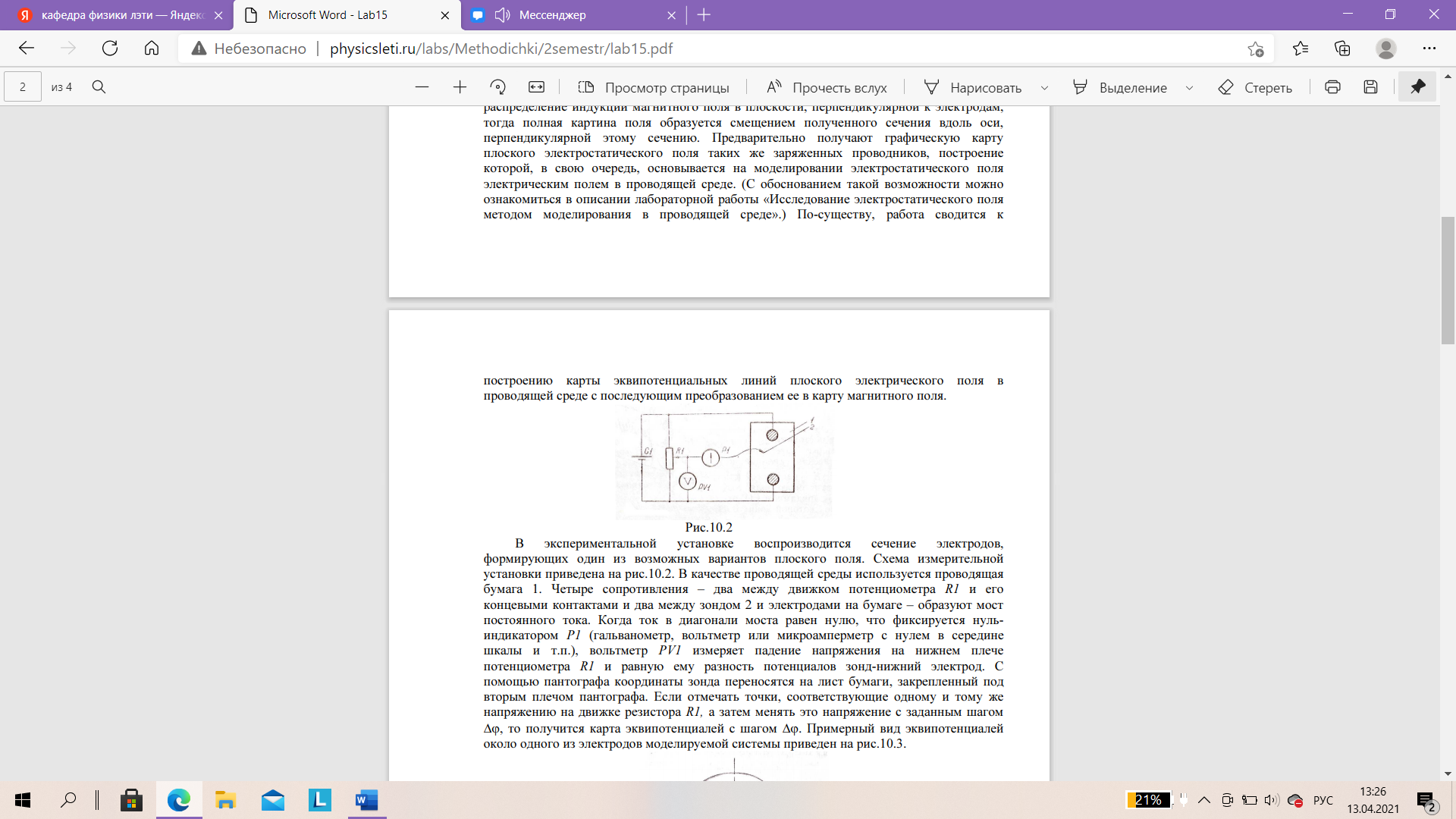 экспериментальной установке воспроизводится сечение электродов, формирующих один из возможных вариантов плоского поля. В качестве проводящей среды используется проводящая бумага 1. Четыре сопротивления – два между движком потенциометра R1 и его концевыми контактами и два между зондом 2 и электродами на бумаге – образуют мост постоянного тока. Когда ток в диагонали моста равен нулю, что фиксируется нуль-индикатором Р1 (гальванометр, вольтметр или микроамперметр с нулем в середине шкалы и т.п.), вольтметр PV1 измеряет падение напряжения на нижнем плече потенциометра R1 и равную ему разность потенциалов зонд-нижний электрод. С помощью пантографа координаты зонда переносятся на лист бумаги, закрепленный под вторым плечом пантографа. Если отмечать точки, соответствующие одному и тому же напряжению на движке резистора R1, а затем менять это напряжение с заданным шагом экспериментальной установке воспроизводится сечение электродов, формирующих один из возможных вариантов плоского поля. В качестве проводящей среды используется проводящая бумага 1. Четыре сопротивления – два между движком потенциометра R1 и его концевыми контактами и два между зондом 2 и электродами на бумаге – образуют мост постоянного тока. Когда ток в диагонали моста равен нулю, что фиксируется нуль-индикатором Р1 (гальванометр, вольтметр или микроамперметр с нулем в середине шкалы и т.п.), вольтметр PV1 измеряет падение напряжения на нижнем плече потенциометра R1 и равную ему разность потенциалов зонд-нижний электрод. С помощью пантографа координаты зонда переносятся на лист бумаги, закрепленный под вторым плечом пантографа. Если отмечать точки, соответствующие одному и тому же напряжению на движке резистора R1, а затем менять это напряжение с заданным шагом 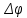 , то получится карта эквипотенциалей с шагом , то получится карта эквипотенциалей с шагом 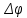 . .Исследуемые закономерности Электрическое и магнитное поля неразрывно связаны между собой, образуя электромагнитное поле. Так, электрический заряд, создающий электростатическое поле в системе отсчета (СО), относительно которой он покоится, создает магнитное поле в СО, относительно которой происходит движение заряда. Р 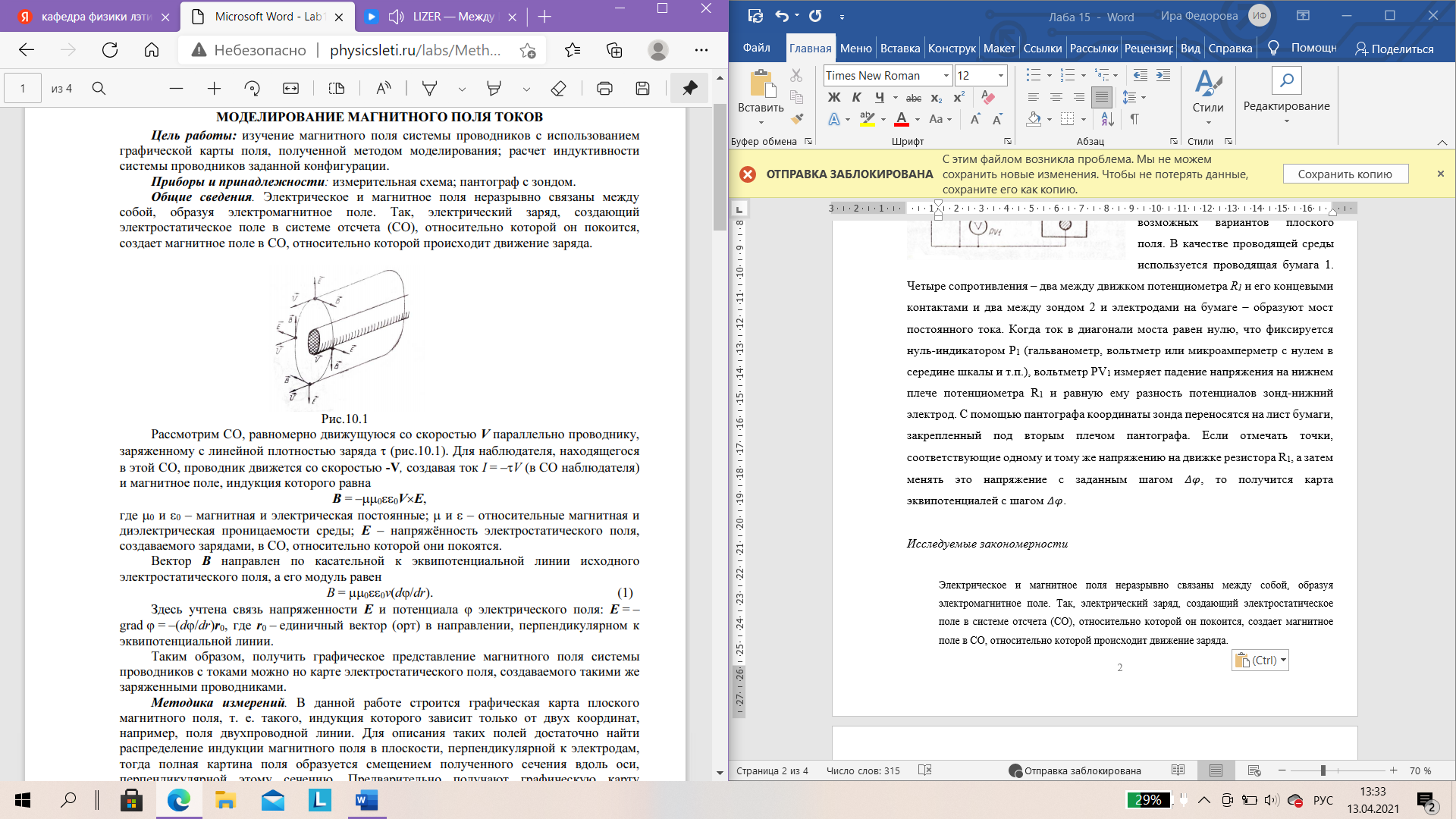 ассмотрим СО, равномерно движущуюся со скоростью V параллельно проводнику, заряженному с линейной плотностью заряда τ. Для наблюдателя, находящегося в этой СО, проводник движется со скоростью -V, создавая ток I = –τV (в СО наблюдателя) и магнитное поле, индукция которого равна B = –µµ0εε0V×E, где µ0 и ε0 – магнитная и электрическая постоянные; µ и ε – относительные магнитная и диэлектрическая проницаемости среды; Е – напряжённость электростатического поля, создаваемого зарядами, в СО, относительно которой они покоятся. ассмотрим СО, равномерно движущуюся со скоростью V параллельно проводнику, заряженному с линейной плотностью заряда τ. Для наблюдателя, находящегося в этой СО, проводник движется со скоростью -V, создавая ток I = –τV (в СО наблюдателя) и магнитное поле, индукция которого равна B = –µµ0εε0V×E, где µ0 и ε0 – магнитная и электрическая постоянные; µ и ε – относительные магнитная и диэлектрическая проницаемости среды; Е – напряжённость электростатического поля, создаваемого зарядами, в СО, относительно которой они покоятся.Вектор В направлен по касательной к эквипотенциальной линии исходного электростатического поля, а его модуль равен B = µµ0εε0 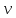 (d (d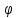 /dr). (1) Здесь учтена связь напряженности E и потенциала /dr). (1) Здесь учтена связь напряженности E и потенциала 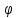 электрического поля: E = – grad электрического поля: E = – grad 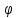 = – (d = – (d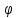 /dr)r0, где r0 – единичный вектор (орт) в направлении, перпендикулярном к эквипотенциальной линии. Таким образом, получить графическое представление магнитного поля системы проводников с токами можно, но карте электростатического поля, создаваемого такими же заряженными проводниками. /dr)r0, где r0 – единичный вектор (орт) в направлении, перпендикулярном к эквипотенциальной линии. Таким образом, получить графическое представление магнитного поля системы проводников с токами можно, но карте электростатического поля, создаваемого такими же заряженными проводниками.Методика измерений 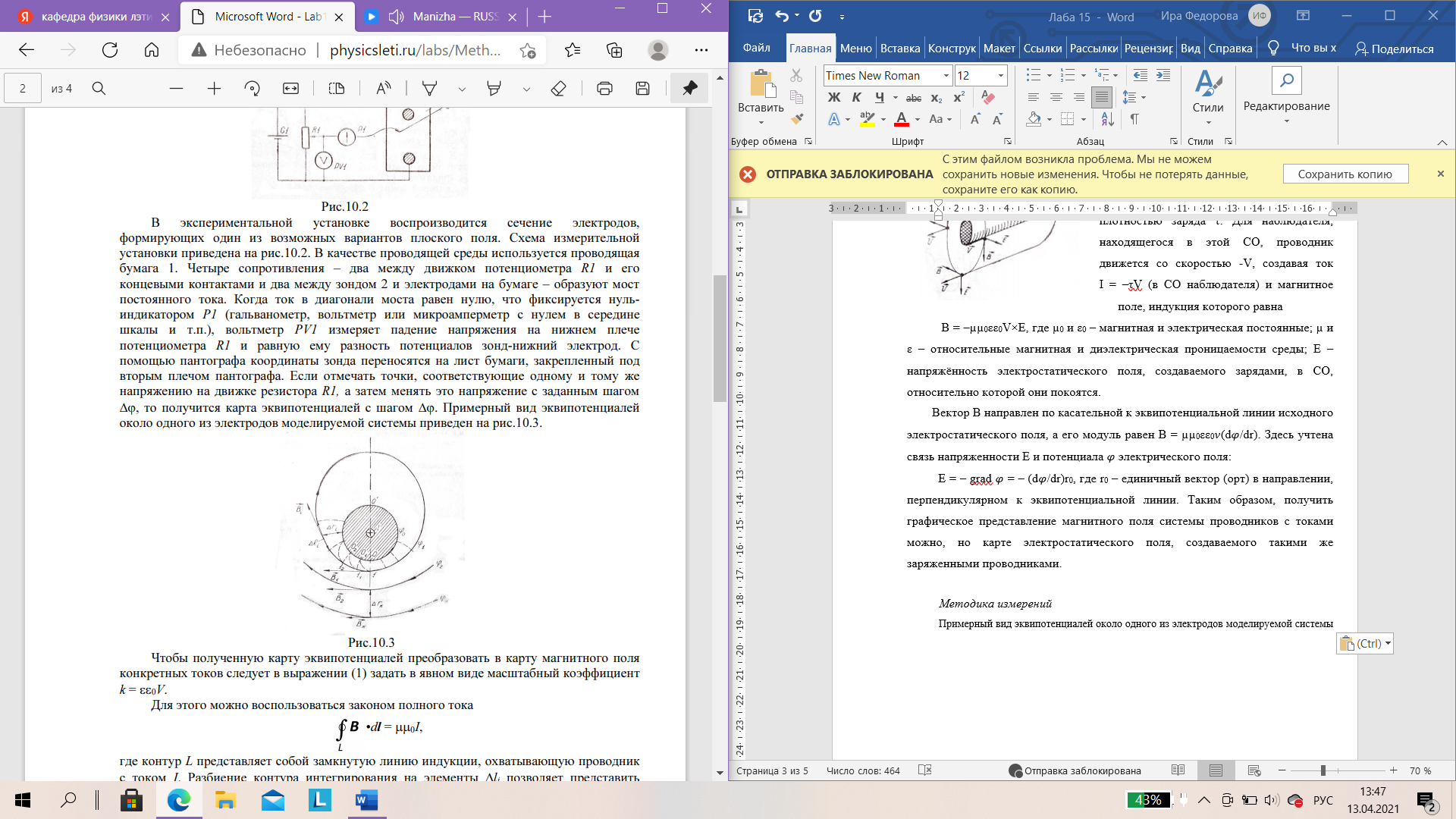 Примерный вид эквипотенциалей около одного из электродов моделируемой системы: Примерный вид эквипотенциалей около одного из электродов моделируемой системы:Чтобы полученную карту эквипотенциалей преобразовать в карту магнитного поля конкретных токов следует в выражении (1) задать в явном виде масштабный коэффициент k = εε0V. Для этого можно воспользоваться законом полного тока 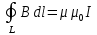 , где контур , где контур 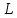 представляет собой замкнутую линию индукции, охватывающую проводник с током представляет собой замкнутую линию индукции, охватывающую проводник с током 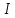 . Разбиение контура интегрирования на элементы . Разбиение контура интегрирования на элементы 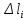 позволяет представить интеграл суммой: позволяет представить интеграл суммой: 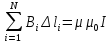 . (2) . (2)Если контуру 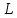 карты магнитного поля сопоставляется ближайшая к электроду эквипотенциаль карты магнитного поля сопоставляется ближайшая к электроду эквипотенциаль 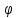 1, то, согласно (1): 1, то, согласно (1): 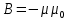 εε0 εε0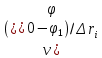 , где , где 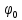 – потенциал электрода. – потенциал электрода.Подставим в (2): εε0 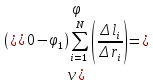 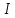 , (3) , (3)Из этого соотношения и определяется масштабный коэффициент k = εε0V после разбиения контура 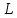 на отрезки на отрезки 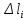 и определения суммы и определения суммы 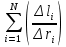 . .Разбиение контура целесообразно начинать от точки 0, лежащей на оси симметрии карты. Вдоль контура электрода влево откладывают отрезок, длина которого равна кратчайшему расстоянию 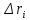 , от точки 0 до соседней линии , от точки 0 до соседней линии 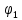 , и получают точку 01. Из точки 01 проводят плавную линию (практически прямую) до пересечения с линией , и получают точку 01. Из точки 01 проводят плавную линию (практически прямую) до пересечения с линией 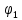 так, чтобы она была перпендикулярна к эквипотенциали так, чтобы она была перпендикулярна к эквипотенциали 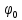 в точке 01 и к эквипотенциали в точке 01 и к эквипотенциали 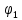 в точке l1. Далее от точки 01 откладывают отрезок, равный расстоянию 01 – l1 и т. д. до точки 0′. Затем подобное построение проводят вправо от точки 0 до точки 0′. в точке l1. Далее от точки 01 откладывают отрезок, равный расстоянию 01 – l1 и т. д. до точки 0′. Затем подобное построение проводят вправо от точки 0 до точки 0′.В описанном варианте разбиения контура на отрезки 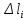 (возможны и другие варианты) все отношения (возможны и другие варианты) все отношения 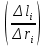 = 1 и = 1 и 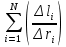 = = 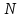 , где , где 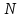 —число участков —число участков 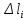 , получившихся на замкнутой линии. Тогда, согласно (3), k = 1/( , получившихся на замкнутой линии. Тогда, согласно (3), k = 1/(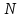 ( (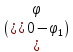 (4) (4)Зная величину масштабного множителя k, индукцию в любой точке карты магнитного поля можно определить по формуле 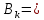 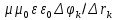 , (5) где , (5) где 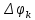 и и 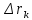 – разность потенциалов и кратчайшее расстояние между ближайшими эквипотенциалями, соответственно, в окрестности рассматриваемой точки. – разность потенциалов и кратчайшее расстояние между ближайшими эквипотенциалями, соответственно, в окрестности рассматриваемой точки.Графическая карта магнитного поля позволяет вычислить индуктивность моделируемой системы проводников. Индуктивность 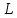 определяется как коэффициент пропорциональности между током определяется как коэффициент пропорциональности между током 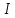 и создаваемым им магнитным потоком и создаваемым им магнитным потоком 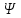 . .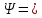 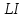 (6) (6)Для приближённого расчета 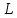 необходимо вычислить магнитный поток через поверхность необходимо вычислить магнитный поток через поверхность 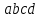 между проводниками: между проводниками: 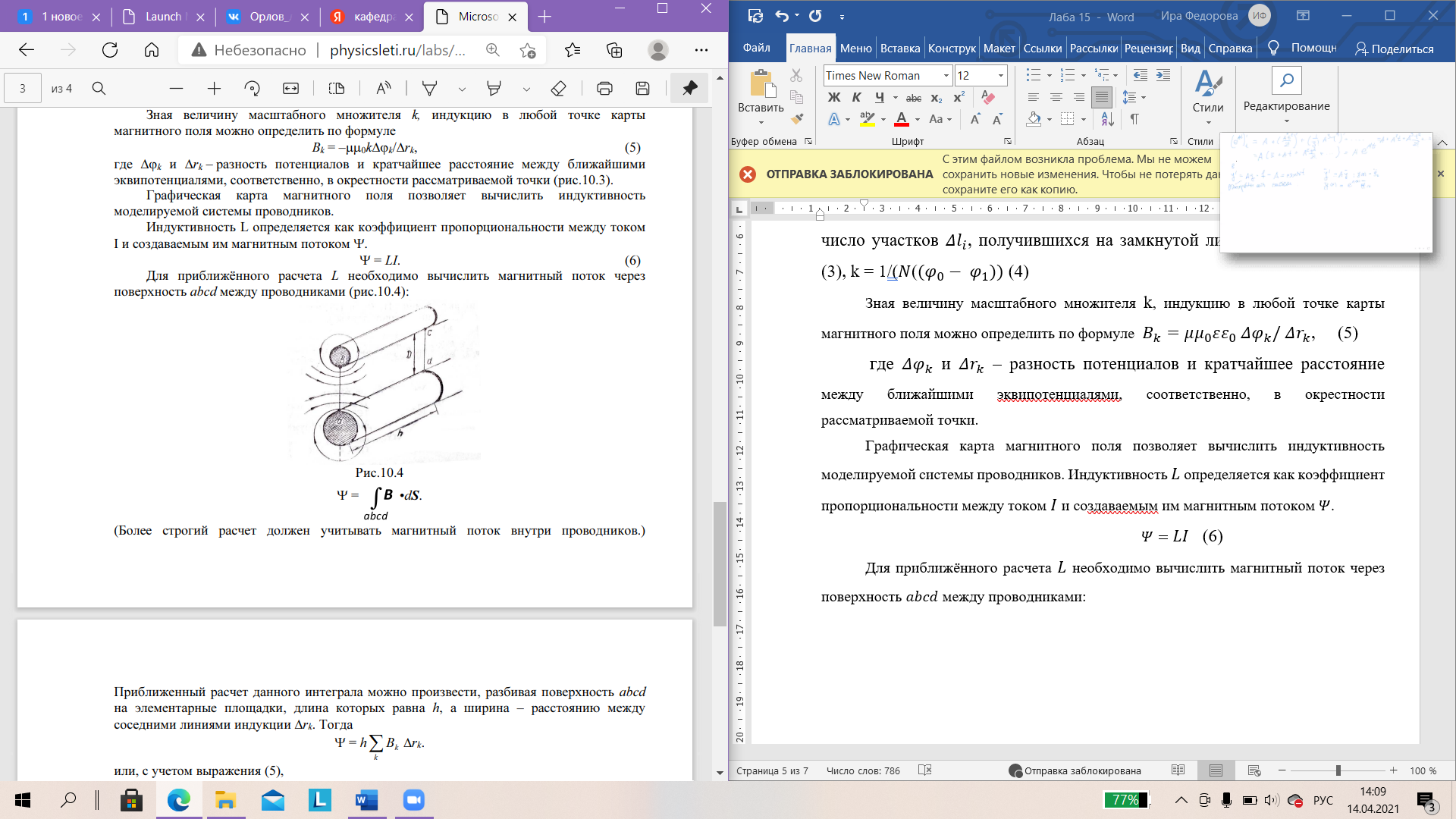 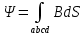 (Более строгий расчет должен учитывать магнитный поток внутри проводников.) Приближенный расчет данного интеграла можно произвести, разбивая поверхность 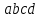 на элементарные площадки, длина которых равна на элементарные площадки, длина которых равна 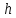 , а ширина – расстоянию между соседними линиями индукции , а ширина – расстоянию между соседними линиями индукции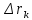 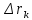 . Тогда . Тогда 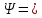 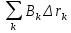 . .Значит 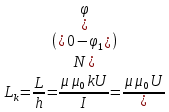 . .
«Моделирование магнитного поля токов»
Обработка результатов Вычислим масштабный коэффициент 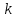 и векторы и векторы 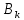 на ближайшей замкнутой линии индукции. на ближайшей замкнутой линии индукции.
Рассчитаем вектор 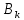 в точках пересечения линии симметрии карты поля с линиями индукции. в точках пересечения линии симметрии карты поля с линиями индукции.
Вычислим погонную индуктивность моделируемой системы 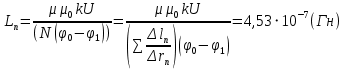 Выведем теоретическое выражение для погонной индуктивности и рассчитаем ее значение, используя геометрические размеры конкретной модели. 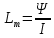 ; ; 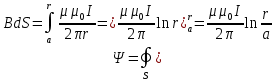 , , где 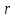 – расстояние между центрами электродов – расстояние между центрами электродов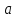 – расстояние между электродом и эквипотенциалью – расстояние между электродом и эквипотенциалью 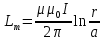 , согласно геометрическим размерам планшета: , согласно геометрическим размерам планшета: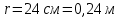 , , 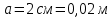 Тогда 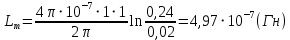 Вывод: в результате лабораторной работы получила теоретическое значение погонной индуктивности равное 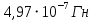 , что примерно равно значению погонной индуктивности , что примерно равно значению погонной индуктивности 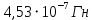 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

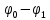 , В
, В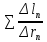
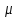
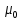 , Гн/м
, Гн/м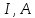
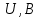

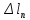 , м
, м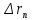 , м
, м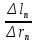
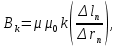
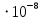 В
В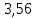
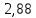
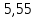
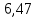
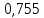
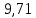
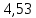
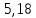
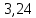
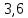
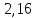
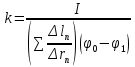
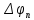 , В
, В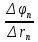 ,
, 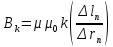 ,
,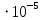 В
В