лаб. раб. 3-11. Лабораторная работа 311 исследование электростатических полей методом моделирования цель работы
 Скачать 268.5 Kb. Скачать 268.5 Kb.
|
ЛАБОРАТОРНАЯ РАБОТА № 3-11 ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ МЕТОДОМ МОДЕЛИРОВАНИЯ Цель работы. Знакомство с методом математического моделирования; исследование электростатического поля заряженных тел. ВВЕДЕНИЕ При исследовании сложных физических процессов широко применяются модельные эксперименты. В ряде случаев модель и натура имеют одинаковую физическую природу, характер самого явления сохраняется, но геометрические размеры модели отличаются от натуры. Это так называемое физическое моделирование. Примером его может служить испытание модели летательного аппарата в аэродинамической трубе. Возможен и другой подход, когда закономерности различных по природе физических явлений описываются одинаковыми дифференциальными уравнениями и граничными условиями. Тождественность математического описания позволяет заменить сложное исследование одного явления более простым исследованием другого. В этом случае имеют дело с математическим моделированием. Компьютерное моделирование, интенсивно развивающееся в последнее время, также может быть отнесено к математическому моделированию. Электростатическое поле в диэлектрике подобно полю постоянного тока в проводящей среде при одинаковой конфигурации электродов. Если потенциалы электродов в обоих случаях одни и те же, то распределение потенциала в диэлектрике такое же, как в проводящей среде с током. Подобие полей видно из следующего сопоставления их свойств. Электростатическое поле в диэлектрике потенциально, циркуляция вектора напряженности электростатического поля Поле в проводящей однородной (без источников сторонних сил) среде также потенциально. Постоянный ток не образует вихрей между электродами. Следовательно, или В соответствии с законом Ома где j — плотность тока, — электропроводность среды. Подставив (3) в (2), получим выражение (1). Таким образом, электрическое поле в проводящей однородной среде подобно электростатическому полю в диэлектрике. Имеется подобие и между граничными условиями. На границе раздела диэлектриков тангенциальная и нормальная составляющие вектора напряженности электрического поля подчиняются условиям E1 = E2 ; ε1En1 = ε2En2 . (4) В проводящей среде непрерывность тангенциальных составляющих следует из потенциальности поля тока. Граничные условия для нормальных составляющих вектора плотности тока следуют из уравнения непрерывности jn1 = jn2 . (5) С учетом (3) γ1En1 = γ2En2 (6) Из подобия граничных условий (4) и (6) следует, что проводящая среда с током может служить моделью для исследования электростатического поля, если проводимость среды заменить диэлектрической проницаемостью , заданной для моделируемого диэлектрика, а электроды в обоих случаях расположить одинаково. Поле в неоднородном диэлектрике, различные области которого имеют неодинаковую диэлектрическую проницаемость , можно также моделировать на проводящей среде, если подобны распределения и . Измерить распределение потенциала в проводящей среде проще, чем в диэлектрике, поэтому исследование на модели зачастую предпочтительнее, чем на электростатическом оригинале. Моделируют плоские поля, потенциал и напряженность которых зависят лишь от двух координат. Плоским является поле в коаксиальном конденсаторе вдали от его концов, в двухпроводной длинной линии, между одиночным проводом и проводящей поверхностью и т.п. На проводящем листе воспроизводится сечение такого поля плоскостью, перпендикулярной электродам. Напряженность электрического поля связана с потенциалом соотношением Если опытным путем найти и построить линии равного потенциала, то напряженность (по модулю) поля в точке, расположенной межу двумя линиями с потенциалами 1 и 2, на расстоянии r: где = 1 - 2. (9) Описание лабораторной установки Схема установки приведена на рис.1. В качестве проводящей среды для модели используют лист текстолита, покрытый проводящей краской (один из планшетов). Планшет закрепляется на Блоке моделирования полей. 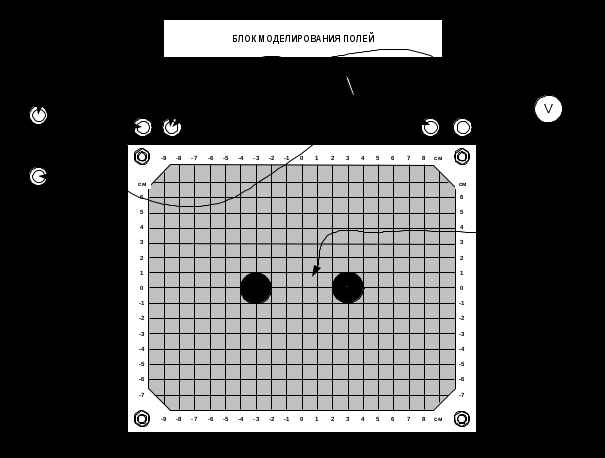 Рис.1. Схема установки для моделирования электростатического поля заряженных тел На гнёзда +Uпит и –Uпит подаётся питание от регулируемого источника напряжения 0…15 В, которое подводится проводами с нижней стороны планшета к медным электродам. Источником напряжения служит генератор напряжения, входящий в состав Блок генераторов напряжений с наборным полем (БГННП). В качестве вольтметра V можно использовать виртуальный прибор на компьютере (предпочтительнее) или мультимер в режиме вольтметра. При использовании виртуального вольтметра его подключают через коннектор. Порядок выполнения работы 1. Установите на блок моделирования полей один из вариантов конфигурации проводящего листа (планшет 1, 2, 3 или 4) и соберите схему, показанную на рис.1. 2. Приготовьте рисунок (миллиметровая бумага, формат А4) с координатной сеткой и расположением электродов, соответствующим выбранному планшету. 3. Включите источник питания и убедитесь, что один из электродов имеет потенциал, равный нулю, а другой – потенциал, равный напряжению источника питания. 4. Выберите такое напряжение питания и U = 10…15 В и шаг изменения потенциала (например, = 1; 1,5; 2 или 2,5 В), чтобы на картине поля получилось 7…10 эквипотенциальных линий. 5. Перемещая зонд от точки нулевого потенциала по оси симметрии к другому электроду, найдите точки с потенциалами 1 = , 2 = 2, 3 = 3 и так далее. Найденные точки отметьте на приготовленном рисунке с координатной сеткой. 6. Перемещая зонд из точки с потенциалом 1 = , вокруг электрода (слегка приближаясь или удаляясь от него), найдите точки равного потенциала и отметьте их на рисунке. Точки равного потенциала соедините плавной кривой. 7. Повторите п.6 для точек с потенциалами 2 = 2, 3 = 3 и т.д. Примечание. В каждом варианте проводящего листа имеются одна или две оси симметрии, поэтому можно ограничиться исследованием половины или четверти проводящей области листа. В результате измерения получите карту эквипотенциалей с заданным шагом . Обработка результатов измерений 1. Построение линий напряженности электрического поля Для построения линий напряженности (силовых линий) используют следующий метод (рис.2). 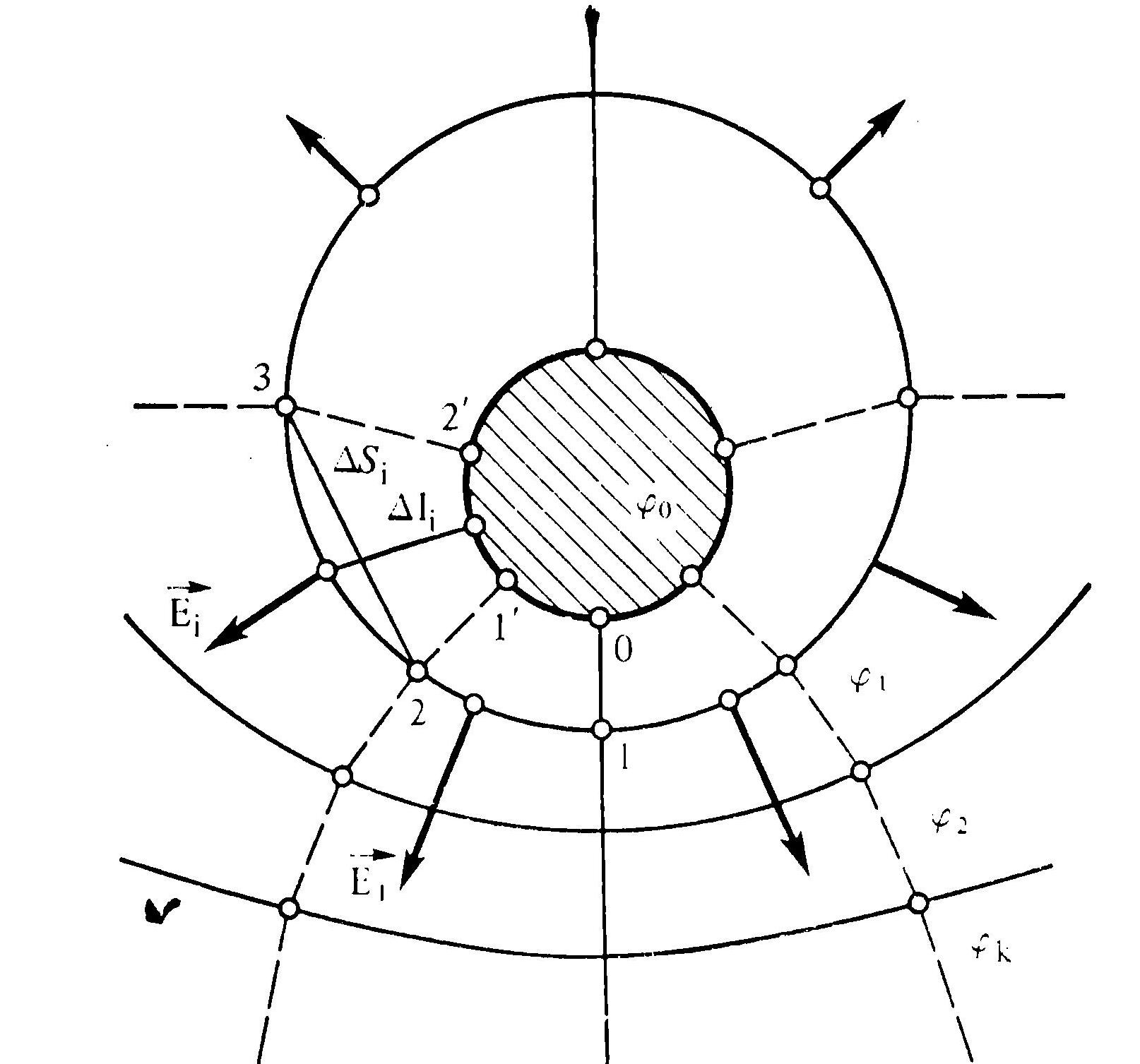 Рис.2. Метод построения линий напряженности (силовых линий) Проводят линию, соединяющую электроды, так, чтобы она совпала с осью симметрии поля. Из точки 0 на поверхности электрода измеряют расстояние 0-1 до ближайшей эквипотенциали. Это расстояние откладывают вдоль поверхности электрода, получая таким образом точку 1' на электроде. Через точку 1' проводят отрезок 1'-2 перпендикулярно поверхности электрода. Откладывают расстояние 1'-2' вдоль поверхности электрода и т.д. Построение заканчивают, дойдя до оси симметрии. Аналогичное построение производят от точки 0 в другую сторону. Каждое построение следует заканчивать таким образом, чтобы длина последнего до оси симметрии отрезка на поверхности электрода была больше длины предпоследнего. Разделив таким образом ближайшую к электроду эквипотенциаль, через полученные точки (1; 2; 3;...) проводят перпендикулярные ей отрезки до пересечения со следующей эквипотенцналью. Когда все эквипотенциали карты окажутся разделенными, полученные точки следует соединить плавными кривыми, соблюдая их ортогональность эквипотенциальным линиям в точках пересечения. 2. Вычисление напряженности электрического поля в произвольных точках Выбирают три точки А, B и С. Точка А расположена в центре между электродами; точка В смещена в сторону примерно на 2 см; точка С смещена еще дальше. Каждая из выбранных точек должна располагаться между двумя эквипотенциальными линиями. Вычислить значения напряженности поля в выбранных точках можно используя формулу (8). 3. Вычисление электрической емкости системы проводников Электрическую емкость системы проводников можно вычислить измерив распределение потенциала в проводящей модели и вычислив градиент (напряженность электрического поля). Будем считать, что ближайшая к электроду эквипотенциаль (1 = ) является деформированным цилиндром. Напряженность поля в пределах каждого отрезка первой эквипотенциали примерно одинакова Погонную емкость системы проводников можно вычислить по формуле Содержание отчета Отчет включает следующее. 1. Принципиальную схему лабораторной установки с пояснениями и характеристиками приборов. 2. Расчетные формулы, использованные в работе. 3. Таблицы с экспериментальными и расчетными данными. 4. Карты эквипотенциалей (бумажный планшет, выдаёт преподаватель). 5. Расчет напряженности поля в выбранных точках. 6. Расчет погонной емкости системы проводников. 6. Выводы по работе. Сравнительную оценку полученных результатов. Контрольные вопросы и задания 1. Какая физическая величина является силовой характеристикой электрического поля? В каких единицах она измеряется? 2. Какая физическая величина является энергетической характеристикой электрического поля? В каких единицах она измеряется? 3. Как связаны между собой напряженность и потенциал электростатического поля? 4. В чем состоит сходство и различие физического и математического моделирования? 5. На каком основании можно заменить исследование электростатического поля изучением поля постоянного тока? 6. Запишите условия на границе раздела двух диэлектриков. 7. Какова взаимная ориентация эквипотенциалей и силовых линий электростатического поля? 8. Дайте определение электроемкости проводника и системы проводников. Литература 1. Детлаф А.А., Яворский Б.М. Курс физики.-М.:Высш.шк.,2007.- 608 с 2. Лабораторный практикум по физике: Учеб. Пособие для студентов втузов/Под ред. К.А.Барсукова и В.Ю.Уханова. – М.: высш.шк., 1988.- 351с. 3. Беглецов Н.Н., Красногорцев И.Л. Электричество и магнетизм. Руководство по выполнению базовых экспериментов. ЭМФ.001 РБЭ (910) Челябинск: ООО «Учебная техника», 2003. 85 с. |
